HybridInstructional.C File Reference

Detailed Description

Example demonstrating usage of HybridCalcultor

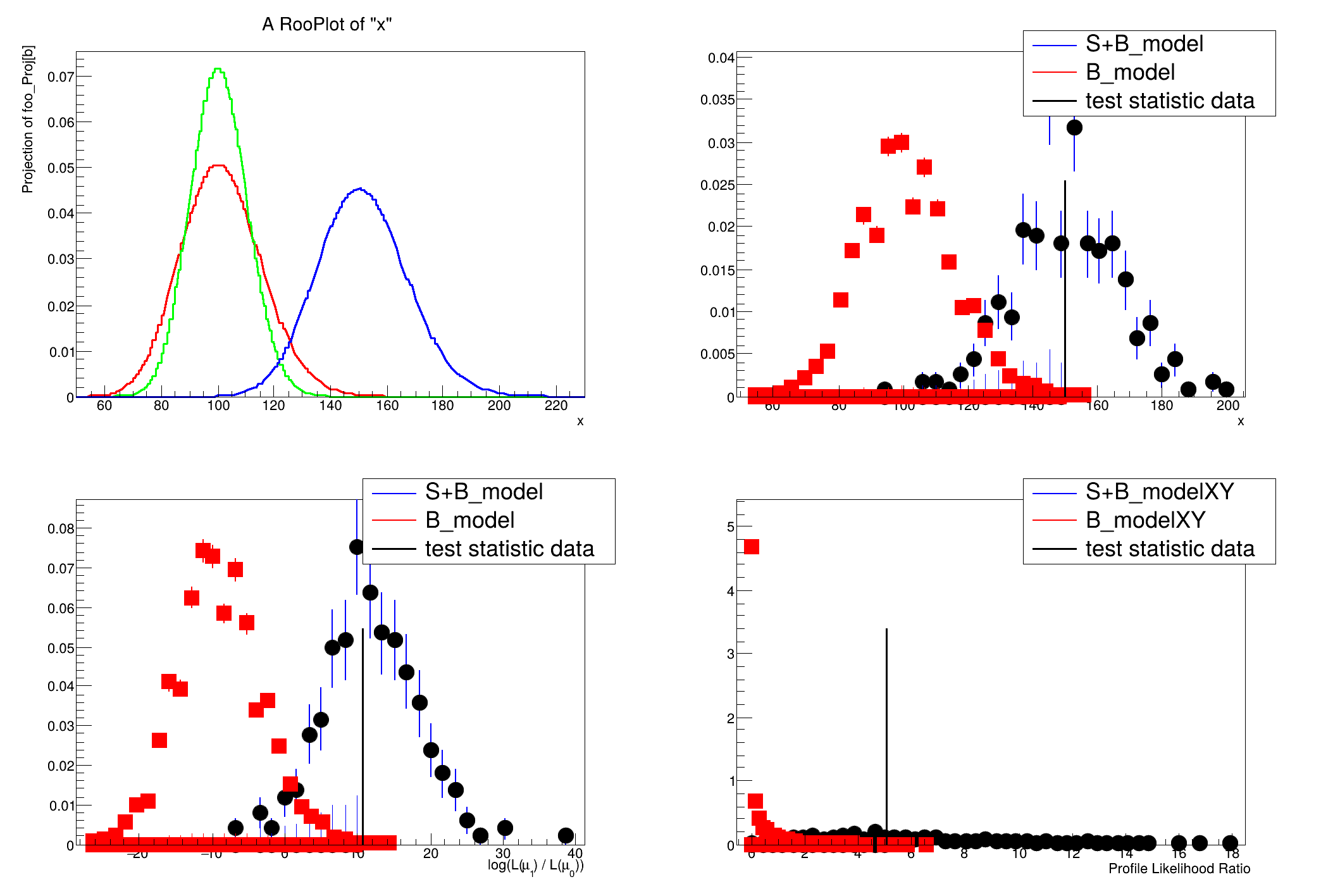
A hypothesis testing example based on number counting with background uncertainty.

NOTE: This example must be run with the ACLIC (the + option ) due to the new class that is defined.

This example:

• demonstrates the usage of the HybridCalcultor (Part 4-6)
• demonstrates the numerical integration of RooFit (Part 2)
• validates the RooStats against an example with a known analytic answer
• demonstrates usage of different test statistics
• explains subtle choices in the prior used for hybrid methods
• demonstrates usage of different priors for the nuisance parameters
• demonstrates usage of PROOF

The basic setup here is that a main measurement has observed x events with an expectation of s+b. One can choose an ad hoc prior for the uncertainty on b, or try to base it on an auxiliary measurement. In this case, the auxiliary measurement (aka control measurement, sideband) is another counting experiment with measurement y and expectation tau*b. With an 'original prior' on b, called $\eta (b)$ then one can obtain a posterior from the auxiliary measurement $\pi (b)=\eta (b)\ast Pois(y|tau\ast b).$ This is a principled choice for a prior on b in the main measurement of x, which can then be treated in a hybrid Bayesian/Frequentist way. Additionally, one can try to treat the two measurements simultaneously, which is detailed in Part 6 of the tutorial.

This tutorial is related to the FourBin.C tutorial in the modeling, but focuses on hypothesis testing instead of interval estimation.

More background on this 'prototype problem' can be found in the following papers:

• Evaluation of three methods for calculating statistical significance when incorporating a systematic uncertainty into a test of the background-only hypothesis for a Poisson process Authors: Robert D. Cousins, James T. Linnemann, Jordan Tucker http://arxiv.org/abs/physics/0702156 NIM A 595 (2008) 480–501
• Statistical Challenges for Searches for New Physics at the LHC Author: Kyle Cranmer http://arxiv.org/abs/physics/0511028
• Measures of Significance in HEP and Astrophysics Authors J. T. Linnemann http://arxiv.org/abs/physics/0312059

 
[#1] INFO:NumericIntegration -- RooRealIntegral::init([py_X_prior_b_X_px]_Norm[b]_denominator_Int[b]) using numeric integrator RooIntegrator1D to calculate Int(b)
-----------------------------------------
Part 2
Hybrid p-value from direct integration = 0.000774094
Z_Gamma Significance  = 3.1655
-----------------------------------------
Part 3
Z_Bi p-value (analytic): 0.00094165
Z_Bi significance (analytic): 3.10804
Real time 0:00:03, CP time 3.830
[#0] WARNING:Eval -- RooStatsUtils::MakeNuisancePdf - no constraints found on nuisance parameters in the input model
[#0] WARNING:Eval -- RooStatsUtils::MakeNuisancePdf - no constraints found on nuisance parameters in the input model
-----------------------------------------
Part 4
 
Results HypoTestCalculator_result: 
 - Null p-value = 0.0005 +/- 0.000288603
 - Significance = 3.29053 +/- 0.162393 sigma
 - Number of Alt toys: 300
 - Number of Null toys: 6000
 - Test statistic evaluated on data: 150
 - CL_b: 0.0005 +/- 0.000288603
 - CL_s+b: 0.506667 +/- 0.0288649
 - CL_s: 1013.33 +/- 587.744
Real time 0:00:00, CP time 0.490
[#0] WARNING:Eval -- RooStatsUtils::MakeNuisancePdf - no constraints found on nuisance parameters in the input model
[#0] WARNING:Eval -- RooStatsUtils::MakeNuisancePdf - no constraints found on nuisance parameters in the input model
-----------------------------------------
Part 5
 
Results HypoTestCalculator_result: 
 - Null p-value = 0.000666667 +/- 0.000333222
 - Significance = 3.20871 +/- 0.143724 sigma
 - Number of Alt toys: 300
 - Number of Null toys: 6000
 - Test statistic evaluated on data: 10.8198
 - CL_b: 0.000666667 +/- 0.000333222
 - CL_s+b: 0.55 +/- 0.0287228
 - CL_s: 825 +/- 414.607
Real time 0:00:00, CP time 0.600
[#0] WARNING:Eval -- RooStatsUtils::MakeNuisancePdf - no constraints found on nuisance parameters in the input model
[#0] WARNING:Eval -- RooStatsUtils::MakeNuisancePdf - no constraints found on nuisance parameters in the input model
-----------------------------------------
Part 6
 
Results HypoTestCalculator_result: 
 - Null p-value = 0.000666667 +/- 0.000333222
 - Significance = 3.20871 +/- 0.143724 sigma
 - Number of Alt toys: 300
 - Number of Null toys: 6000
 - Test statistic evaluated on data: 5.03388
 - CL_b: 0.000666667 +/- 0.000333222
 - CL_s+b: 0.493333 +/- 0.0288649
 - CL_s: 740 +/- 372.402
Real time 0:00:03, CP time 3.910

 
#include "RooGlobalFunc.h"
#include "RooRealVar.h"
#include "RooProdPdf.h"
#include "RooWorkspace.h"
#include "RooDataSet.h"
#include "TCanvas.h"
#include "TStopwatch.h"
#include "TH1.h"
#include "RooPlot.h"
#include "RooMsgService.h"
 
#include "RooStats/NumberCountingUtils.h"
 
#include "RooStats/HybridCalculator.h"
#include "RooStats/ToyMCSampler.h"
#include "RooStats/HypoTestPlot.h"
 
#include "RooStats/ProfileLikelihoodTestStat.h"
#include "RooStats/SimpleLikelihoodRatioTestStat.h"
#include "RooStats/RatioOfProfiledLikelihoodsTestStat.h"
#include "RooStats/MaxLikelihoodEstimateTestStat.h"
 
using namespace RooFit;
using namespace RooStats;
 
// ----------------------------------
// A New Test Statistic Class for this example.
// It simply returns the sum of the values in a particular
// column of a dataset.
// You can ignore this class and focus on the macro below
class BinCountTestStat : public TestStatistic {
public:
   BinCountTestStat(void) : fColumnName("tmp") {}
   BinCountTestStat(string columnName) : fColumnName(columnName) {}
 
   virtual Double_t Evaluate(RooAbsData &data, RooArgSet & /*nullPOI*/)
   {
      // This is the main method in the interface
      Double_t value = 0.0;
      for (int i = 0; i < data.numEntries(); i++) {
         value += data.get(i)->getRealValue(fColumnName.c_str());
      }
      return value;
   }
   virtual const TString GetVarName() const { return fColumnName; }
 
private:
   string fColumnName;
 
protected:
   ClassDef(BinCountTestStat, 1)
};
 
ClassImp(BinCountTestStat)
 
// ----------------------------------
// The Actual Tutorial Macro
 
void HybridInstructional(int ntoys = 6000)
{
   double nToysRatio = 20;      // ratio Ntoys Null/ntoys ALT
 
   // This tutorial has 6 parts
   // Table of Contents
   // Setup
   //   1. Make the model for the 'prototype problem'
   // Special cases
   //   2. Use RooFit's direct integration to get p-value & significance
   //   3. Use RooStats analytic solution for this problem
   // RooStats HybridCalculator -- can be generalized
   //   4. RooStats ToyMC version of 2. & 3.
   //   5. RooStats ToyMC with an equivalent test statistic
   //   6. RooStats ToyMC with simultaneous control & main measurement
 
   // It takes ~4 min without PROOF and ~2 min with PROOF on 4 cores.
   // Of course, everything looks nicer with more toys, which takes longer.
 
   TStopwatch t;
   t.Start();
   TCanvas *c = new TCanvas;
   c->Divide(2, 2);
 
   // ----------------------------------------------------
   // P A R T   1  :  D I R E C T   I N T E G R A T I O N
   // ====================================================
   // Make model for prototype on/off problem
   // $Pois(x | s+b) * Pois(y | tau b )$
   // for Z_Gamma, use uniform prior on b.
   RooWorkspace *w = new RooWorkspace("w");
   w->factory("Poisson::px(x[150,0,500],sum::splusb(s[0,0,100],b[100,0.1,300]))");
   w->factory("Poisson::py(y[100,0.1,500],prod::taub(tau[1.],b))");
   w->factory("PROD::model(px,py)");
   w->factory("Uniform::prior_b(b)");
 
   // We will control the output level in a few places to avoid
   // verbose progress messages.  We start by keeping track
   // of the current threshold on messages.
   RooFit::MsgLevel msglevel = RooMsgService::instance().globalKillBelow();
 
   // Use PROOF-lite on multi-core machines
   ProofConfig *pc = NULL;
   // uncomment below if you want to use PROOF
   // ~~~
   // pc = new ProofConfig(*w, 4, "workers=4", kFALSE); // machine with 4 cores
   // pc = new ProofConfig(*w, 2, "workers=2", kFALSE); // machine with 2 cores
   // ~~~
 
   // ----------------------------------------------------
   // P A R T   2  :  D I R E C T   I N T E G R A T I O N
   // ====================================================
   // This is not the 'RooStats' way, but in this case the distribution
   // of the test statistic is simply x and can be calculated directly
   // from the PDF using RooFit's built-in integration.
   // Note, this does not generalize to situations in which the test statistic
   // depends on many events (rows in a dataset).
 
   // construct the Bayesian-averaged model (eg. a projection pdf)
   // $p'(x|s) = \int db p(x|s+b) * [ p(y|b) * prior(b) ]$
   w->factory("PROJ::averagedModel(PROD::foo(px|b,py,prior_b),b)");
 
   RooMsgService::instance().setGlobalKillBelow(RooFit::ERROR); // lower message level
   // plot it, red is averaged model, green is b known exactly, blue is s+b av model
   RooPlot *frame = w->var("x")->frame(Range(50, 230));
   w->pdf("averagedModel")->plotOn(frame, LineColor(kRed));
   w->pdf("px")->plotOn(frame, LineColor(kGreen));
   w->var("s")->setVal(50.);
   w->pdf("averagedModel")->plotOn(frame, LineColor(kBlue));
   c->cd(1);
   frame->Draw();
   w->var("s")->setVal(0.);
 
   // compare analytic calculation of Z_Bi
   // with the numerical RooFit implementation of Z_Gamma
   // for an example with x = 150, y = 100
 
   // numeric RooFit Z_Gamma
   w->var("y")->setVal(100);
   w->var("x")->setVal(150);
   std::unique_ptr<RooAbsReal> cdf{w->pdf("averagedModel")->createCdf(*w->var("x"))};
   cdf->getVal(); // get ugly print messages out of the way
   cout << "-----------------------------------------" << endl;
   cout << "Part 2" << endl;
   cout << "Hybrid p-value from direct integration = " << 1 - cdf->getVal() << endl;
   cout << "Z_Gamma Significance  = " << PValueToSignificance(1 - cdf->getVal()) << endl;
   RooMsgService::instance().setGlobalKillBelow(msglevel); // set it back
 
   // ---------------------------------------------
   // P A R T   3  :  A N A L Y T I C   R E S U L T
   // =============================================
   // In this special case, the integrals are known analytically
   // and they are implemented in RooStats::NumberCountingUtils
 
   // analytic Z_Bi
   double p_Bi = NumberCountingUtils::BinomialWithTauObsP(150, 100, 1);
   double Z_Bi = NumberCountingUtils::BinomialWithTauObsZ(150, 100, 1);
   cout << "-----------------------------------------" << endl;
   cout << "Part 3" << endl;
   std::cout << "Z_Bi p-value (analytic): " << p_Bi << std::endl;
   std::cout << "Z_Bi significance (analytic): " << Z_Bi << std::endl;
   t.Stop();
   t.Print();
   t.Reset();
   t.Start();
 
   // -------------------------------------------------------------
   // P A R T   4  :  U S I N G   H Y B R I D   C A L C U L A T O R
   // =============================================================
   // Now we demonstrate the RooStats HybridCalculator.
   //
   // Like all RooStats calculators it needs the data and a ModelConfig
   // for the relevant hypotheses.  Since we are doing hypothesis testing
   // we need a ModelConfig for the null (background only) and the alternate
   // (signal+background) hypotheses.  We also need to specify the PDF,
   // the parameters of interest, and the observables.  Furthermore, since
   // the parameter of interest is floating, we need to specify which values
   // of the parameter corresponds to the null and alternate (eg. s=0 and s=50)
   //
   // define some sets of variables obs={x} and poi={s}
   // note here, x is the only observable in the main measurement
   // and y is treated as a separate measurement, which is used
   // to produce the prior that will be used in this calculation
   // to randomize the nuisance parameters.
   w->defineSet("obs", "x");
   w->defineSet("poi", "s");
 
   // create a toy dataset with the x=150
   RooDataSet *data = new RooDataSet("d", "d", *w->set("obs"));
   data->add(*w->set("obs"));
 
   // Part 3a : Setup ModelConfigs
   // -------------------------------------------------------
   // create the null (background-only) ModelConfig with s=0
   ModelConfig b_model("B_model", w);
   b_model.SetPdf(*w->pdf("px"));
   b_model.SetObservables(*w->set("obs"));
   b_model.SetParametersOfInterest(*w->set("poi"));
   w->var("s")->setVal(0.0); // important!
   b_model.SetSnapshot(*w->set("poi"));
 
   // create the alternate (signal+background) ModelConfig with s=50
   ModelConfig sb_model("S+B_model", w);
   sb_model.SetPdf(*w->pdf("px"));
   sb_model.SetObservables(*w->set("obs"));
   sb_model.SetParametersOfInterest(*w->set("poi"));
   w->var("s")->setVal(50.0); // important!
   sb_model.SetSnapshot(*w->set("poi"));
 
   // Part 3b : Choose Test Statistic
   // ----------------------------------
   // To make an equivalent calculation we need to use x as the test
   // statistic.  This is not a built-in test statistic in RooStats
   // so we define it above.  The new class inherits from the
   // RooStats::TestStatistic interface, and simply returns the value
   // of x in the dataset.
 
   BinCountTestStat binCount("x");
 
   // Part 3c : Define Prior used to randomize nuisance parameters
   // -------------------------------------------------------------
   //
   // The prior used for the hybrid calculator is the posterior
   // from the auxiliary measurement y.  The model for the aux.
   // measurement is Pois(y|tau*b), thus the likelihood function
   // is proportional to (has the form of) a Gamma distribution.
   // if the 'original prior' $\eta(b)$ is uniform, then from
   // Bayes's theorem we have the posterior:
   // $\pi(b) = Pois(y|tau*b) * \eta(b)$
   // If $\eta(b)$ is flat, then we arrive at a Gamma distribution.
   // Since RooFit will normalize the PDF we can actually supply
   // $py=Pois(y,tau*b)$ that will be equivalent to multiplying by a uniform.
   //
   // Alternatively, we could explicitly use a gamma distribution:
   // `w->factory("Gamma::gamma(b,sum::temp(y,1),1,0)");`
   //
   // or we can use some other ad hoc prior that do not naturally
   // follow from the known form of the auxiliary measurement.
   // The common choice is the equivalent Gaussian:
   w->factory("Gaussian::gauss_prior(b,y, expr::sqrty('sqrt(y)',y))");
   // this corresponds to the "Z_N" calculation.
   //
   // or one could use the analogous log-normal prior
   w->factory("Lognormal::lognorm_prior(b,y, expr::kappa('1+1./sqrt(y)',y))");
   //
   // Ideally, the HybridCalculator would be able to inspect the full
   // model $Pois(x | s+b) * Pois(y | tau b )$ and be given the original
   // prior $\eta(b)$ to form $\pi(b) = Pois(y|tau*b) * \eta(b)$.
   // This is not yet implemented because in the general case
   // it is not easy to identify the terms in the PDF that correspond
   // to the auxiliary measurement.  So for now, it must be set
   // explicitly with:
   //  - ForcePriorNuisanceNull()
   //  - ForcePriorNuisanceAlt()
   // the name "ForcePriorNuisance" was chosen because we anticipate
   // this to be auto-detected, but will leave the option open
   // to force to a different prior for the nuisance parameters.
 
   // Part 3d : Construct and configure the HybridCalculator
   // -------------------------------------------------------
 
   HybridCalculator hc1(*data, sb_model, b_model);
   ToyMCSampler *toymcs1 = (ToyMCSampler *)hc1.GetTestStatSampler();
   toymcs1->SetNEventsPerToy(1);         // because the model is in number counting form
   toymcs1->SetTestStatistic(&binCount); // set the test statistic
   hc1.SetToys(ntoys, ntoys / nToysRatio);
   hc1.ForcePriorNuisanceAlt(*w->pdf("py"));
   hc1.ForcePriorNuisanceNull(*w->pdf("py"));
   // if you wanted to use the ad hoc Gaussian prior instead
   // ~~~
   //  hc1.ForcePriorNuisanceAlt(*w->pdf("gauss_prior"));
   //  hc1.ForcePriorNuisanceNull(*w->pdf("gauss_prior"));
   // ~~~
   // if you wanted to use the ad hoc log-normal prior instead
   // ~~~
   //  hc1.ForcePriorNuisanceAlt(*w->pdf("lognorm_prior"));
   //  hc1.ForcePriorNuisanceNull(*w->pdf("lognorm_prior"));
   // ~~~
 
   // enable proof
   // NOTE: This test statistic is defined in this macro, and is not
   // working with PROOF currently.  Luckily test stat is fast to evaluate.
   //  `if(pc) toymcs1->SetProofConfig(pc);`
 
   // these lines save current msg level and then kill any messages below ERROR
   RooMsgService::instance().setGlobalKillBelow(RooFit::ERROR);
   // Get the result
   HypoTestResult *r1 = hc1.GetHypoTest();
   RooMsgService::instance().setGlobalKillBelow(msglevel); // set it back
   cout << "-----------------------------------------" << endl;
   cout << "Part 4" << endl;
   r1->Print();
   t.Stop();
   t.Print();
   t.Reset();
   t.Start();
 
   c->cd(2);
   HypoTestPlot *p1 = new HypoTestPlot(*r1, 30); // 30 bins, TS is discrete
   p1->Draw();
 
   // -------------------------------------------------------------------------
   // # P A R T   5  :  U S I N G   H Y B R I D   C A L C U L A T O R
   // # W I T H   A N   A L T E R N A T I V E   T E S T   S T A T I S T I C
   //
   // A likelihood ratio test statistics should be 1-to-1 with the count x
   // when the value of b is fixed in the likelihood.  This is implemented
   // by the SimpleLikelihoodRatioTestStat
 
   SimpleLikelihoodRatioTestStat slrts(*b_model.GetPdf(), *sb_model.GetPdf());
   slrts.SetNullParameters(*b_model.GetSnapshot());
   slrts.SetAltParameters(*sb_model.GetSnapshot());
 
   // HYBRID CALCULATOR
   HybridCalculator hc2(*data, sb_model, b_model);
   ToyMCSampler *toymcs2 = (ToyMCSampler *)hc2.GetTestStatSampler();
   toymcs2->SetNEventsPerToy(1);
   toymcs2->SetTestStatistic(&slrts);
   hc2.SetToys(ntoys, ntoys / nToysRatio);
   hc2.ForcePriorNuisanceAlt(*w->pdf("py"));
   hc2.ForcePriorNuisanceNull(*w->pdf("py"));
   // if you wanted to use the ad hoc Gaussian prior instead
   // ~~~
   //  hc2.ForcePriorNuisanceAlt(*w->pdf("gauss_prior"));
   //  hc2.ForcePriorNuisanceNull(*w->pdf("gauss_prior"));
   // ~~~
   // if you wanted to use the ad hoc log-normal prior instead
   // ~~~
   //  hc2.ForcePriorNuisanceAlt(*w->pdf("lognorm_prior"));
   //  hc2.ForcePriorNuisanceNull(*w->pdf("lognorm_prior"));
   // ~~~
 
   // enable proof
   if (pc)
      toymcs2->SetProofConfig(pc);
 
   // these lines save current msg level and then kill any messages below ERROR
   RooMsgService::instance().setGlobalKillBelow(RooFit::ERROR);
   // Get the result
   HypoTestResult *r2 = hc2.GetHypoTest();
   cout << "-----------------------------------------" << endl;
   cout << "Part 5" << endl;
   r2->Print();
   t.Stop();
   t.Print();
   t.Reset();
   t.Start();
   RooMsgService::instance().setGlobalKillBelow(msglevel);
 
   c->cd(3);
   HypoTestPlot *p2 = new HypoTestPlot(*r2, 30); // 30 bins
   p2->Draw();
 
   // -----------------------------------------------------------------------------
   // # P A R T   6  :  U S I N G   H Y B R I D   C A L C U L A T O R   W I T H   A N   A L T E R N A T I V E   T E S T
   // # S T A T I S T I C   A N D   S I M U L T A N E O U S   M O D E L
   //
   // If one wants to use a test statistic in which the nuisance parameters
   // are profiled (in one way or another), then the PDF must constrain b.
   // Otherwise any observation x can always be explained with s=0 and b=x/tau.
   //
   // In this case, one is really thinking about the problem in a
   // different way.  They are considering x,y simultaneously.
   // and the PDF should be $Pois(x | s+b) * Pois(y | tau b )$
   // and the set 'obs' should be {x,y}.
 
   w->defineSet("obsXY", "x,y");
 
   // create a toy dataset with the x=150, y=100
   w->var("x")->setVal(150.);
   w->var("y")->setVal(100.);
   RooDataSet *dataXY = new RooDataSet("dXY", "dXY", *w->set("obsXY"));
   dataXY->add(*w->set("obsXY"));
 
   // now we need new model configs, with PDF="model"
   ModelConfig b_modelXY("B_modelXY", w);
   b_modelXY.SetPdf(*w->pdf("model")); // IMPORTANT
   b_modelXY.SetObservables(*w->set("obsXY"));
   b_modelXY.SetParametersOfInterest(*w->set("poi"));
   w->var("s")->setVal(0.0); // IMPORTANT
   b_modelXY.SetSnapshot(*w->set("poi"));
 
   // create the alternate (signal+background) ModelConfig with s=50
   ModelConfig sb_modelXY("S+B_modelXY", w);
   sb_modelXY.SetPdf(*w->pdf("model")); // IMPORTANT
   sb_modelXY.SetObservables(*w->set("obsXY"));
   sb_modelXY.SetParametersOfInterest(*w->set("poi"));
   w->var("s")->setVal(50.0); // IMPORTANT
   sb_modelXY.SetSnapshot(*w->set("poi"));
 
   // without this print, their can be a crash when using PROOF.  Strange.
   //  w->Print();
 
   // Test statistics like the profile likelihood ratio
   // (or the ratio of profiled likelihoods (Tevatron) or the MLE for s)
   // will now work, since the nuisance parameter b is constrained by y.
   // ratio of alt and null likelihoods with background yield profiled.
   //
   // NOTE: These are slower because they have to run fits for each toy
 
   // Tevatron-style Ratio of profiled likelihoods
   // $Q_Tev = -log L(s=0,\hat\hat{b})/L(s=50,\hat\hat{b})$
   RatioOfProfiledLikelihoodsTestStat ropl(*b_modelXY.GetPdf(), *sb_modelXY.GetPdf(), sb_modelXY.GetSnapshot());
   ropl.SetSubtractMLE(false);
 
   // profile likelihood where alternate is best fit value of signal yield
   // $\lambda(0) = -log L(s=0,\hat\hat{b})/L(\hat{s},\hat{b})$
   ProfileLikelihoodTestStat profll(*b_modelXY.GetPdf());
 
   // just use the maximum likelihood estimate of signal yield
   // $MLE = \hat{s}$
   MaxLikelihoodEstimateTestStat mlets(*sb_modelXY.GetPdf(), *w->var("s"));
 
   // However, it is less clear how to justify the prior used in randomizing
   // the nuisance parameters (since that is a property of the ensemble,
   // and y is a property of each toy pseudo experiment.  In that case,
   // one probably wants to consider a different y0 which will be held
   // constant and the prior $\pi(b) = Pois(y0 | tau b) * \eta(b)$.
   w->factory("y0[100]");
   w->factory("Gamma::gamma_y0(b,sum::temp0(y0,1),1,0)");
   w->factory("Gaussian::gauss_prior_y0(b,y0, expr::sqrty0('sqrt(y0)',y0))");
 
   // HYBRID CALCULATOR
   HybridCalculator hc3(*dataXY, sb_modelXY, b_modelXY);
   ToyMCSampler *toymcs3 = (ToyMCSampler *)hc3.GetTestStatSampler();
   toymcs3->SetNEventsPerToy(1);
   toymcs3->SetTestStatistic(&slrts);
   hc3.SetToys(ntoys, ntoys / nToysRatio);
   hc3.ForcePriorNuisanceAlt(*w->pdf("gamma_y0"));
   hc3.ForcePriorNuisanceNull(*w->pdf("gamma_y0"));
   // if you wanted to use the ad hoc Gaussian prior instead
   // ~~~{.cpp}
   // hc3.ForcePriorNuisanceAlt(*w->pdf("gauss_prior_y0"));
   // hc3.ForcePriorNuisanceNull(*w->pdf("gauss_prior_y0"));
   // ~~~
 
   // choose fit-based test statistic
   toymcs3->SetTestStatistic(&profll);
   // toymcs3->SetTestStatistic(&ropl);
   // toymcs3->SetTestStatistic(&mlets);
 
   // enable proof
   if (pc)
      toymcs3->SetProofConfig(pc);
 
   // these lines save current msg level and then kill any messages below ERROR
   RooMsgService::instance().setGlobalKillBelow(RooFit::ERROR);
   // Get the result
   HypoTestResult *r3 = hc3.GetHypoTest();
   cout << "-----------------------------------------" << endl;
   cout << "Part 6" << endl;
   r3->Print();
   t.Stop();
   t.Print();
   t.Reset();
   t.Start();
   RooMsgService::instance().setGlobalKillBelow(msglevel);
 
   c->cd(4);
   c->GetPad(4)->SetLogy();
   HypoTestPlot *p3 = new HypoTestPlot(*r3, 50); // 50 bins
   p3->Draw();
 
   c->SaveAs("zbi.pdf");
 
   // -----------------------------------------
   // OUTPUT W/O PROOF (2.66 GHz Intel Core i7)
   // =========================================
 
   // -----------------------------------------
   // Part 2
   // Hybrid p-value from direct integration = 0.00094165
   // Z_Gamma Significance  = 3.10804
   // -----------------------------------------
   //
   // Part 3
   // Z_Bi p-value (analytic): 0.00094165
   // Z_Bi significance (analytic): 3.10804
   // Real time 0:00:00, CP time 0.610
 
   // -----------------------------------------
   // Part 4
   // Results HybridCalculator_result:
   // - Null p-value = 0.00115 +/- 0.000228984
   // - Significance = 3.04848 sigma
   // - Number of S+B toys: 1000
   // - Number of B toys: 20000
   // - Test statistic evaluated on data: 150
   // - CL_b: 0.99885 +/- 0.000239654
   // - CL_s+b: 0.476 +/- 0.0157932
   // - CL_s: 0.476548 +/- 0.0158118
   // Real time 0:00:07, CP time 7.620
 
   // -----------------------------------------
   // Part 5
   // Results HybridCalculator_result:
   // - Null p-value = 0.0009 +/- 0.000206057
   // - Significance = 3.12139 sigma
   // - Number of S+B toys: 1000
   // - Number of B toys: 20000
   // - Test statistic evaluated on data: 10.8198
   // - CL_b: 0.9991 +/- 0.000212037
   // - CL_s+b: 0.465 +/- 0.0157726
   // - CL_s: 0.465419 +/- 0.0157871
   // Real time 0:00:34, CP time 34.360
 
   // -----------------------------------------
   // Part 6
   // Results HybridCalculator_result:
   // - Null p-value = 0.000666667 +/- 0.000149021
   // - Significance = 3.20871 sigma
   // - Number of S+B toys: 1000
   // - Number of B toys: 30000
   // - Test statistic evaluated on data: 5.03388
   // - CL_b: 0.999333 +/- 0.000149021
   // - CL_s+b: 0.511 +/- 0.0158076
   // - CL_s: 0.511341 +/- 0.0158183
   // Real time 0:05:06, CP time 306.330
 
   // ---------------------------------------------------------
   // OUTPUT w/ PROOF (2.66 GHz Intel Core i7, 4 virtual cores)
   // =========================================================
 
   // -----------------------------------------
   // Part 5
   // Results HybridCalculator_result:
   // - Null p-value = 0.00075 +/- 0.000173124
   // - Significance = 3.17468 sigma
   // - Number of S+B toys: 1000
   // - Number of B toys: 20000
   // - Test statistic evaluated on data: 10.8198
   // - CL_b: 0.99925 +/- 0.000193577
   // - CL_s+b: 0.454 +/- 0.0157443
   // - CL_s: 0.454341 +/- 0.0157564
   // Real time 0:00:16, CP time 0.990
 
   // -----------------------------------------
   // Part 6
   // Results HybridCalculator_result:
   // - Null p-value = 0.0007 +/- 0.000152699
   // - Significance = 3.19465 sigma
   // - Number of S+B toys: 1000
   // - Number of B toys: 30000
   // - Test statistic evaluated on data: 5.03388
   // - CL_b: 0.9993 +/- 0.000152699
   // - CL_s+b: 0.518 +/- 0.0158011
   // - CL_s: 0.518363 +/- 0.0158124
   // Real time 0:01:25, CP time 0.580
 
   // ----------------------------------
   // Comparison
   // ----------------------------------
   // LEPStatToolsForLHC
   // https://plone4.fnal.gov:4430/P0/phystat/packages/0703002
   // Uses Gaussian prior
   // CL_b = 6.218476e-04, Significance = 3.228665 sigma
   //
   // ----------------------------------
   // Comparison
   // ----------------------------------
   // Asymptotic
   // From the value of the profile likelihood ratio (5.0338)
   // The significance can be estimated using Wilks's theorem
   // significance = sqrt(2*profileLR) = 3.1729 sigma
}

Authors

Kyle Cranmer, Wouter Verkerke, and Sven Kreiss

Definition in file HybridInstructional.C.