Class structure for Root Finder methods

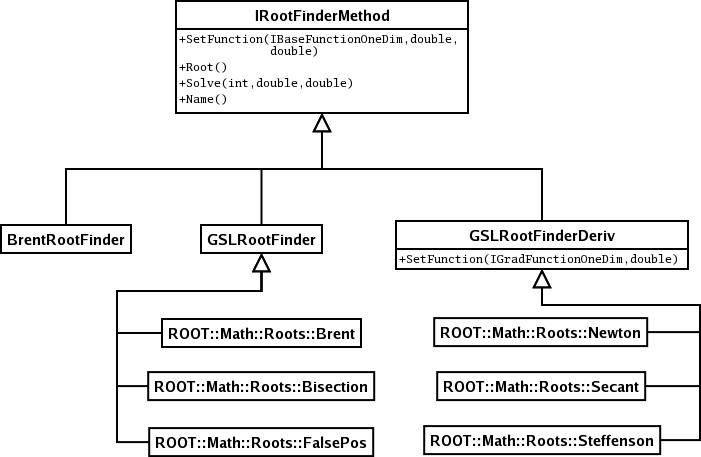
The next image shows the classes provided in ROOT to calculate the root of a function. They all work with functions in one dimension, although some methods need also to calculate the derivative of the functions. All the methods, except the one implemented in BrentRootFinder are taken from the GSL library.

Using an existing Root Finder method

Using the class directly

The classes shown in the previous diagram are described and used as follows:

• BrentRootFinder: This is the only class that is implemented without wrapping methods from GSL. It implements the Brent method to find the root of a given function. Example:

  #include "TF1.h"
  #include "Math/WrappedTF1.h"
  #include "Math/BrentRootFinder.h"
   
  int NumericalRootFinder()
  {
   
     // Create the function and wrap it
     TF1 f("Sin Function", "sin(x)", TMath::PiOver2(), TMath::TwoPi() );
     ROOT::Math::WrappedTF1 wf1(f);
   
     // Create the Integrator
     ROOT::Math::BrentRootFinder brf;
   
     // Set parameters of the method
     brf.SetFunction( wf1, TMath::PiOver2(), TMath::TwoPi() );
     brf.Solve();
   
     cout << brf.Root() << endl;
   
     return 0;
  }

• GSLRootFinder: This class is only a helper for the classes that derivate from it. It should not be used directly, as the next three classes handle all the missing behaviour. All the classes deriving from this just wrap the different GSL methods that do not need to use the derivative to find the root of the given function.
• ROOT::Math::Roots::Brent: Wraps the Brent method implemented in the GSL into the GSLRootFinder class. Example:

  #include "TF1.h"
  #include "Math/WrappedTF1.h"
  #include "Math/RootFinderAlgorithms.h"
   
  int NumericalRootFinder()
  {
   
     // Create the function and wrap it
     TF1 f("Sin Function", "sin(x)", TMath::PiOver2(), TMath::TwoPi() );
     ROOT::Math::WrappedTF1 wf1(f);
   
     // Create the Integrator
     ROOT::Math::Roots::Brent brf;
   
     // Set parameters of the method
     brf.SetFunction( wf1, TMath::PiOver2(), TMath::TwoPi() );
     brf.Solve();
   
     cout << brf.Root() << endl;
   
     return 0;
  }

• ROOT::Math::Roots::Bisection: Wraps the bisection method implemented in the GSL into the GSLRootFinder. Example:

  #include "TF1.h"
  #include "Math/WrappedTF1.h"
  #include "Math/RootFinderAlgorithms.h"
   
  int NumericalRootFinder()
  {
   
     // Create the function and wrap it
     TF1 f("Sin Function", "sin(x)", TMath::PiOver2(), TMath::TwoPi() );
     ROOT::Math::WrappedTF1 wf1(f);
   
     // Create the Integrator
     ROOT::Math::Roots::Bisection brf;
   
     // Set parameters of the method
     brf.SetFunction( wf1, TMath::PiOver2(), TMath::TwoPi() );
     brf.Solve();
   
     cout << brf.Root() << endl;
   
     return 0;
  }

• ROOT::Math::Roots::FalsePos: Wraps the false postion method implemented in the GSL into the GSLRootFinder class. Example:

  #include "TF1.h"
  #include "Math/WrappedTF1.h"
  #include "Math/RootFinderAlgorithms.h"
   
  int NumericalRootFinder()
  {
   
     // Create the function and wrap it
     TF1 f("Sin Function", "sin(x)", TMath::PiOver2(), TMath::TwoPi() );
     ROOT::Math::WrappedTF1 wf1(f);
   
     // Create the Integrator
     ROOT::Math::Roots::FalsePos brf;
   
     // Set parameters of the method
     brf.SetFunction( wf1, TMath::PiOver2(), TMath::TwoPi() );
     brf.Solve();
   
     cout << brf.Root() << endl;
   
     return 0;
  }

• GSLRootFinderDeriv::Base class for GSL Root-Finding algorithms for one dimensional functions which use function derivatives. As with GSLRootFinder users should not use this class directly but instantiate the template ROOT::Math::RootFinder class with the corresponding algorithms.
• ROOT::Math::Roots::Newton:Wraps the Newton method implemented in the GSL. Example:

  #include "Math/Functor.h"
  #include "Math/RootFinderAlgorithms.h"
   
  double myfunc(double x ) { 
     return sin(x); 
  }
   
  double myfunc_deriv ( double x ) { 
     return cos(x); 
  }
   
  int NumericalRootFinder()
  {
   
     ROOT::Math::GradFunctor1D f1(&myfunc, &myfunc_deriv);
   
     // Create the Integrator
     ROOT::Math::Roots::Newton rf;
   
     rf.SetFunction(f1, TMath::Pi() - 1); 
   
     rf.Solve();
   
     cout << rf.Root() << endl;
   
     return 0;
  }

• ROOT::Math::Roots::Secant:Wraps the Secant method implemented in the GSL. Example:

  #include "Math/Functor.h"
  #include "Math/RootFinderAlgorithms.h"
   
  double myfunc(double x ) { 
     return sin(x); 
  }
   
  double myfunc_deriv ( double x ) { 
     return cos(x); 
  }
   
  int NumericalRootFinder()
  {
   
     ROOT::Math::GradFunctor1D f1(&myfunc, &myfunc_deriv);
   
     // Create the Integrator
     ROOT::Math::Roots::Secant rf;
   
     rf.SetFunction(f1, TMath::Pi() - 1); 
   
     rf.Solve();
   
     cout << rf.Root() << endl;
   
     return 0;
  }

• ROOT::Math::Roots::Steffenson::Wraps the Steffenson method implemented in the GSL. Example:

  #include "Math/Functor.h"
  #include "Math/RootFinderAlgorithms.h"
   
  double myfunc(double x ) { 
     return sin(x); 
  }
   
  double myfunc_deriv ( double x ) { 
     return cos(x); 
  }
   
  int NumericalRootFinder()
  {
   
     ROOT::Math::GradFunctor1D f1(&myfunc, &myfunc_deriv);
   
     // Create the Integrator
     ROOT::Math::Roots::Steffenson rf;
   
     rf.SetFunction(f1, TMath::Pi() - 1); 
   
     rf.Solve();
   
     cout << rf.Root() << endl;
   
     return 0;
  }

Using the Plug-In Mananger

As with the other numerical algorithms in ROOT, there is the possibility of avoinding the use of all the low lever classes through the plug-in manager. Using the class ROOT::Math::RootFinder we can just create any of the existing methods through its constructor and work with it as if we where working with a IRootFinderMethod. Example:

#include "Math/Functor.h"
#include "Math/RootFinder.h"
 
double myfunc(double x ) { 
   return sin(x); 
}
 
double myfunc_deriv ( double x ) { 
   return cos(x); 
}
 
int NumericalRootFinder()
{
 
   // RootFinder with Base Functions
   ROOT::Math::Functor1D f1D(&myfunc);
 
   // Create the Integrator
   ROOT::Math::RootFinder rfb(ROOT::Math::RootFinder::kBRENT);
   rfb.SetFunction(f1D, TMath::PiOver2(), TMath::TwoPi()); 
   rfb.Solve();
   cout << rfb.Root() << endl;
 
   ROOT::Math::RootFinder rfbis(ROOT::Math::RootFinder::kGSL_BISECTION );
   rfbis.SetFunction(f1D, TMath::PiOver2(), TMath::TwoPi()); 
   rfbis.Solve();
   cout << rfbis.Root() << endl;
 
   ROOT::Math::RootFinder rffp(ROOT::Math::RootFinder::kGSL_FALSE_POS);
   rffp.SetFunction(f1D, TMath::PiOver2(), TMath::TwoPi()); 
   rffp.Solve();
   cout << rffp.Root() << endl;
 
   ROOT::Math::RootFinder rfgb(ROOT::Math::RootFinder::kGSL_BRENT);
   rfgb.SetFunction(f1D, TMath::PiOver2(), TMath::TwoPi()); 
   rfgb.Solve();
   cout << rfgb.Root() << endl;
 
   // RootFinder with derivative functions
   ROOT::Math::GradFunctor1D f1DG(&myfunc, &myfunc_deriv);
 
   ROOT::Math::RootFinder rfn(ROOT::Math::RootFinder::kGSL_NEWTON);
   rfn.SetFunction(f1DG, TMath::Pi() - 1);
   rfn.Solve();
   cout << rfn.Root() << endl;
 
   ROOT::Math::RootFinder rfsec(ROOT::Math::RootFinder::kGSL_SECANT);
   rfsec.SetFunction(f1DG, TMath::Pi() - 1);
   rfsec.Solve();
   cout << rfsec.Root() << endl;
 
   ROOT::Math::RootFinder rfst(ROOT::Math::RootFinder::kGSL_STEFFENSON);
   rfst.SetFunction(f1DG, TMath::Pi() - 1);
   rfst.Solve();
   cout << rfst.Root() << endl;
 
   return 0;
}

This example shows how to create all the classes previously seen through the ROOT::Math::RootFinder class and its enumeration type in the constructor. It can be seen that the way it is used is exactly as in the examples before.

How to implement your own Integrator

Pending of confirmation to do!