How to implement a mathematical function inside the framework

Implementing an existing interface

To get a consistency in the mathematical methods within ROOT, there exists a set of interfaces to define the basic behaviour of a mathematical function. In order to use the classes presented in this chapter, the mathematical functions defined by the user must inherit from any of the classes seen in the figure:

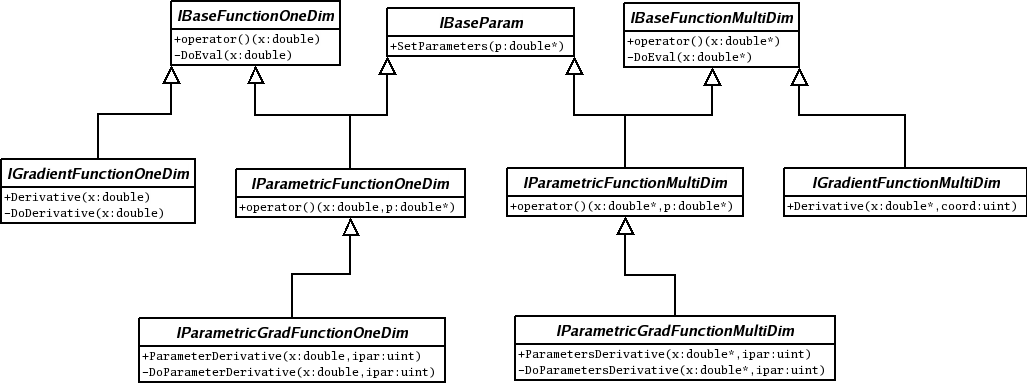
One Dimensional Functions

For the case of defining functions in one dimension, the user will have to derivate their own classes from the following:

IBaseFunctionOneDim: This class is the most basic function. Provides a method to evaluate the function given a value (simple double) by implementing operator() (const double ). The user class defined only needs to reimplement the method DoEval(double x), that will do the work of evaluating the function at point x. Example:

#include "Math/IFunction.h"
class MyFunction: public ROOT::Math::IBaseFunctionOneDim{
   double DoEval(double x) const{
      return x*x;
   }
   ROOT::Math::IBaseFunctionOneDim* Clone() const{
      return new MyFunction();
   }
};

Example 1: How to create a class that represents a mathematical function. The user only has to override two methods from IBaseFunctionOneDim:

IGradientFunctionOneDim: Some of the classes presented in this chapter will need to calculate the derivatives of the function. In these cases, the user will have to provide the neccesary code for this to happen. The interface defined in IGradientFunctionOneDim introduced the method Derivative(double x) that will return the derivative of the function at the point x. The class inherit by the user will have to implement the abstract method DoDerivative(double x), leaving the rest of the class untouched. Example:

#include "Math/IFunction.h"
class MyGradientFunction: public ROOT::Math::IGradientFunctionOneDim{
public:
   double DoEval(double x) const{
      return sin(x);
   }
   ROOT::Math::IBaseFunctionOneDim* Clone() const{
      return new MyGradientFunction();
   }
   double DoDerivative(double x) const{
      return -cos(x);
   }
}; </pre>
    <p>Example 2: A gradient function just needs to add a method      that calculates the derivative to the functionality of      <kbd>IBaseFunctionOneDim</kbd>.</p>
    </div>
    </li>
    <li><dfn>IParametricFunctionOneDim</dfn>: This is a specialized   interface for one-dimensional parametric functions. It defines  the <kbd>operator() (double x, const double* p)</kbd> that  will set the parameters of the functions with vector  <kbd>p</kbd>, and then will perform   <kbd>IBaseFunctionOneDim::operator() (double  x)</kbd>. However, the user will have to provide extra  functionality only for <kbd>IBaseParam::SetParameters(double*   p)</kbd>. Example:
    <pre ><cpp>
#include "Math/IFunction.h"
#include "Math/IParamFunction.h"
class MyParametricFunction: public ROOT::Math::IParametricFunctionOneDim{
private:
   const double *pars;
 
public:
   double DoEvalPar(double x,const double* p) const{
      return (x * p[0]) + (x * x * p[1]);
   }
   ROOT::Math::IBaseFunctionOneDim* Clone() const{
      return new MyParametricFunction();
   }
   const double* Parameters() const{
      return pars;
   }
   void SetParameters(const double* p){
      pars = p;
   }
   unsigned int NPar() const{
      return 2;
   }
};

Example 3: How to implement a parametric function in one dimension. Notice how the user has to implement five functions, from which two of them are from the previous case.

IParametricGradFunctionOneDim: This is the most complex base class of all. It accumulates the methods from both IGradientFunctioOneDim and IParametricFunctionOneDim. Rarely used, but needed in some cases. Example:

#include "Math/IFunction.h"
#include "Math/IParamFunction.h"
 
class MyParametricGradFunction: 
           public ROOT::Math::IParametricGradFunctionOneDim{
private:
   const double *pars;
 
public:
   double DoEvalPar(double x, const double* p) const{
      return sin(x)*p[0];
   }
   ROOT::Math::IBaseFunctionOneDim* Clone() const{
      return new MyParametricGradFunction();
   }
   double DoParameterDerivative(double x, const double* p, unsigned int ipar) const{
      return x*cos(x)*p[ipar];
   }
   const double* Parameters() const {
      return pars;
   }
   void SetParameters(const double* p){
      pars = p;
   }
 
   unsigned int NPar() const{
      return 1;
   }
};

Example 4: In this case, the user has to implement a considerable number of functions.

Multi Dimensional Functions

The most generic case of a multidimensional function has similar approach. Some examples will be shown next. It is important to notice, that one dimensional functions can be also implemented through the interfaces that will be presented here. Nevertheless, we encourage the user to implement those following the indications of the previous chapter, as the efficiency is better in that case.

IBaseFunctionMultiDim: This interface provides the operator() (const double*) that takes an array of doubles with all the values for the different dimensions. In this case, the user has to provide the functionality for two different functions: DoEval(const double*) and NDim(). The first ones evaluates the function given the array that represents the multiple variables. The second returns the number of dimensions of the function. Example:

#include "Math/IFunction.h"
class MyFunction: public ROOT::Math::IBaseFunctionMultiDim{
public:
   double DoEval(const double* x) const{
      return x[0] + sin(x[1]);
   }
 
   unsigned int NDim() const{
      return 2;
   }
 
   ROOT::Math::IBaseFunctionMultiDim* Clone() const{
      return new MyFunction();
   }
 
};

Example 5: A Basic Multidimensional Function.

IGradientFunctionMultiDim: This interface offers the same functionality as the base function plus the calcualtion of the derivative. It only adds the Derivative(double* x, uint ipar) method for the user to implement. This method must implement the derivative of the function with respect to the variable indicated with the second parameter. Example:

#include "Math/IFunction.h"
class MyGradientFunction: public ROOT::Math::IGradientFunctionMultiDim{
public:
   double DoEval(const double* x) const{
      return x[0] + sin(x[1]);
   }
   unsigned int NDim() const{
      return 2;
   }
   ROOT::Math::IGradientFunctionMultiDim* Clone() const{
      return new MyGradientFunction();
   }
   double DoDerivative(const double* x, unsigned int ipar) const{
      if ( ipar == 0 )
         return sin(x[1]);
      else
         return x[0] + x[1] * cos(x[1]);
   }
 
};

Example 6: The simplest gradient function.

IParametricFunctionMultiDim: Describes a multi dimensional parametric function. Similarly to the one dimensional version, the user needs to provide the method SetParameters(double* p) as well as the getter methods Parameters() and NPar(). Example:

#include "Math/IFunction.h"
#include "Math/IParamFunction.h"
 
class MyParametricFunction: public ROOT::Math::IParametricFunctionMultiDim
{
private:
   const double* pars;
 
public:
   double DoEvalPar(const double* x, const double* p) const{
      return p[0] * x[0] + sin(x[1]) + p[1];
   }
 
   unsigned int NDim() const{
      return 2;
   }
   ROOT::Math::IParametricFunctionMultiDim* Clone() const{
      return new MyParametricFunction();
   }
 
   const double* Parameters() const{
      return pars;
   }
 
   void SetParameters(const double* p){
      pars = p;
   }
 
   unsigned int NPar() const{
      return 2;
   }
 
};

Example 7: How to implement a multidimension parametric function.

IParametricGradFunctionMultiDim: Provides an interface for parametric gradient multi-dimensional functions in addition to function evaluation and gradient with respect the coordinates and the gradient with respect to the parameters, via the method ParameterGradient(). This interface is hardly used. Example:

#include "Math/IFunction.h"
#include "Math/IParamFunction.h"
 
class MyParametricGradFunction: 
          public ROOT::Math::IParametricGradFunctionMultiDim{
private:
   const double* pars;
 
public:
   double DoEvalPar(const double* x, const double* p) const{
      return p[0] * x[0] + sin(x[1]) + p[1];
   }
   unsigned int NDim() const{
      return 2;
   }
   ROOT::Math::IParametricGradFunctionMultiDim* Clone() const{
      return new MyParametricGradFunction();
   }
   const double* Parameters() const {
      return pars;
   }
   void SetParameters(const double* p){
      pars = p;
   }
   unsigned int NPar() const{
      return 2;
   }
   double DoParameterDerivative(const double* x, const double* p, unsigned int ipar) const{
      if ( ipar == 0 )
         return sin(x[1]) + p[1];
      else
         return p[0] * x[0] + x[1] * cos(x[1]) + p[1];
   }
};

Example 8: How to implement a multidimensional parametric function with the derivative functionality.

Adapting a function: Wrappers.

There is another possible way of creating mathematical functions that can be understood by ROOT without the need to implement an predefined interface. This is through function wrappers. Here we will introduce wrappers for the most basic functions, refering further documentation to the online reference.

There is one possible wrapper for every interface explained in the previous section. The following table indicates the wrapper for the most basic ones:

Interface	Function Wrapper
IBaseFunctionOneDim	Functor1D
IGradientFunctionOneDim	GradFunctor1D
IBaseFunctionMultiDim	Functor
IGradientFunctionMultiDim	GradFunctor

Wrapping One Dimensional Functions

Functor1D:Used to wrap one-dimensional functions It can wrap all the following types:

A free C function of type double ()(double ).
Any C++ callable object implemention double operator()( const double ).
A member function with the correct signature like Foo::Eval(const double ). In this case one pass the object pointer and a pointer to the member function (&Foo::Eval).

#include "Math/Functor.h"
class MyFunction1D { 
 
public: 
 
   double operator()(double x) const { 
      return x*x; 
   } 
   double Eval(double x) const { return x+x; }
};
 
double freeFunction1D(double  x ) { 
   return 2*x; 
}
int function()
{
   // test free function
   ROOT::Math::Functor1D  f1(&freeFunction1D); 
 
   MyFunction1D myf1;
 
   // test from function object
   ROOT::Math::Functor1D  f2(myf1); 
 
   // test from member function 
   ROOT::Math::Functor1D f3(&myf1,&MyFunction1D::Eval); 
 
   cout << f1(2) << endl;
   cout << f2(2) << endl;
   cout << f3(2) << endl;
 
   return 0;
}

Example 9: Wrapping a one dimensional function with Functor1D.

GradFunctor1D: Class used to wrap one-dimensional gradient functions. It can be constructed in three different ways:

Any object implementing both double operator()( double) for the function evaluation and double Derivative(double) for the partial derivatives.
Any object implementing any member function like Foo::XXX(double ) for the function evaluation and any other member function like Foo::YYY(double ) for the derivative.
Any two function objects implementing double operator()( double ) . One object provides the function evaluation, the other the derivative.
A free C function of type double ()(double ).

#include "Math/Functor.h"
class MyFunction1D { 
 
public: 
 
   double operator()(double x) const { return x*x; } 
 
   double Eval(double x) const { return x+x; }
 
   double Derivative(double x) const { return 2*x; }
};
 
double freeFunction1D(double  x ) { 
   return x*x; 
}
 
int function(){
   MyFunction1D myf1;
 
   // from function object implementing both
   ROOT::Math::GradFunctor1D  f1(myf1); 
 
   // test grad functor from object and member functions
   ROOT::Math::GradFunctor1D  f2(&myf1,&MyFunction1D::Eval, 
                                 &MyFunction1D::Derivative); 
 
   // test from a free C function and a function object
   ROOT::Math::GradFunctor1D  f3(&freeFunction1D,myf1); 
 
   cout << f1(3) << endl;
   cout << f2(3) << endl;
   cout << f3(3) << endl;
 
   return 0;
}

Example 10: Wrapping a one dimensional gradient function with GradFunctor1D.

Wrapping Multi Dimensional Functions

Functor: It is used to wrap in a very simple and convenient way multi-dimensional function objects. It can wrap all the following types:

Any C++ callable object implemention double operator()( const double * ).
A free C function of type double ()(const double *).
A member function with the correct signature like Foo::Eval(const double * ). In this case one pass the object pointer and a pointer to the member function (&Foo::Eval).

The function dimension is required when constructing the functor.

#include "Math/Functor.h"
class MyFunction { 
 
public: 
   double operator()(const double *x) const { 
      return x[0]+x[1]; 
   } 
   double Eval(const double * x) const { return x[0]+x[1]; }
};
 
double freeFunction(const double * x ) { 
   return x[0]+x[1]; 
}
 
int function(){
   // test directly calling the function object
   MyFunction myf;
 
   // test from a free function pointer
   ROOT::Math::Functor f1(&freeFunction,2); 
 
   // test from function object
   ROOT::Math::Functor f2(myf,2); 
 
   // test from a member function 
   ROOT::Math::Functor f3(&myf,&MyFunction::Eval,2); 
 
   double x[] = {1,2};
 
   cout << f1(x) << endl;
   cout << f2(x) << endl;
   cout << f3(x) << endl;
 
   return 0;
}

Example 11: Wrapping a multi dimensional function with Functor.

GradFunctor: It is used to wrap in a very C++ callable object to make gradient functions. It can be constructed in three different way:

From an object implementing both double operator()(const double * ) for the function evaluation and double Derivative(const double *, int icoord) for the partial derivatives.
From an object implementing any member function like Foo::XXX(const double *) for the function evaluation and any member function like Foo::XXX(const double *, int icoord) for the partial derivatives.
From an function object implementing double operator()( const double * ) for the function evaluation and another function object implementing double operator() (const double *, int icoord) for the partial derivatives.

The function dimension is required when constructing the functor.

#include "Math/Functor.h"
class MyFunction { 
 
public: 
   double operator()(const double *x) const { 
      return x[0]+x[1]; 
   } 
 
   double Derivative(const double * x, int /* icoord */) const
          { return x[0]+x[1]; }
   double Eval(const double * x) const { return x[0]+x[1]; }
};
 
double freeDerivativeFunction(const double * x, int /* icoord */ ) { 
   return x[0]+x[1]; 
}
 
int function(){
   MyFunction myf;
 
   // test grad functor from an object providing eval and deriv.
   ROOT::Math::GradFunctor  f1(myf,2); 
 
   // test grad functor from object and member functions
   ROOT::Math::GradFunctor  f2(&myf,&MyFunction::Eval, 
                               &MyFunction::Derivative, 2); 
 
   // test from a function object and a free C function
   ROOT::Math::GradFunctor  f3(myf, &freeDerivativeFunction, 2); 
 
   double x[] = {1,2};
 
   cout << f1(x) << endl;
   cout << f2(x) << endl;
   cout << f3(x) << endl;
 
   return 0;
}

Example 12: Wrapping a multi dimensional gradient function with GradFunctor.

Special case: Wrapping a TF1

In many cases, the user works with the TF1 class instead of with defined C functions. The mathematical library in ROOT provides some solutions to wrap these into the interfaces needed by other methods.

When a TF1 defines a one dimensional function, it can be wrapped using ROOT::Math::WrappedTF1. The default constructor takes a TF1 as an argument, that will be wrapped with the interfaces of a IParametricGradFunctionOneDim. Example:

#include "TF1.h"
#include "Math/WrappedTF1.h"
 
int function()
{
   TF1 f("Sin Function", "sin(x)+y",0,3);
 
   ROOT::Math::WrappedTF1 wf1(f);
 
   cout << f(1) << endl;
   cout << wf1(1) << endl;
 
   return 0;
}

Example 13: How to wrap a one dimensional TF1.

For a TF1 defining a multidimensional function, the class to use is ROOT::Math::WrappedMultiTF1. Following the usual procedure, setting the TF1 though the constructor, will wrap it into a IParametricFunctionMultiDim. Example:

#include "TF1.h"
#include "Math/WrappedMultiTF1.h"
 
int function()
{
   TF1 f("Sin Function", "sin(x) + y",0,3);
   ROOT::Math::WrappedMultiTF1 wf1(f);
   double x[] = {1,2};
 
   cout << f(x) << endl;
   cout << wf1(x) << endl;
 
   return 0;
}

Example 14: How to wrap a multi dimensional TF1.

You are here