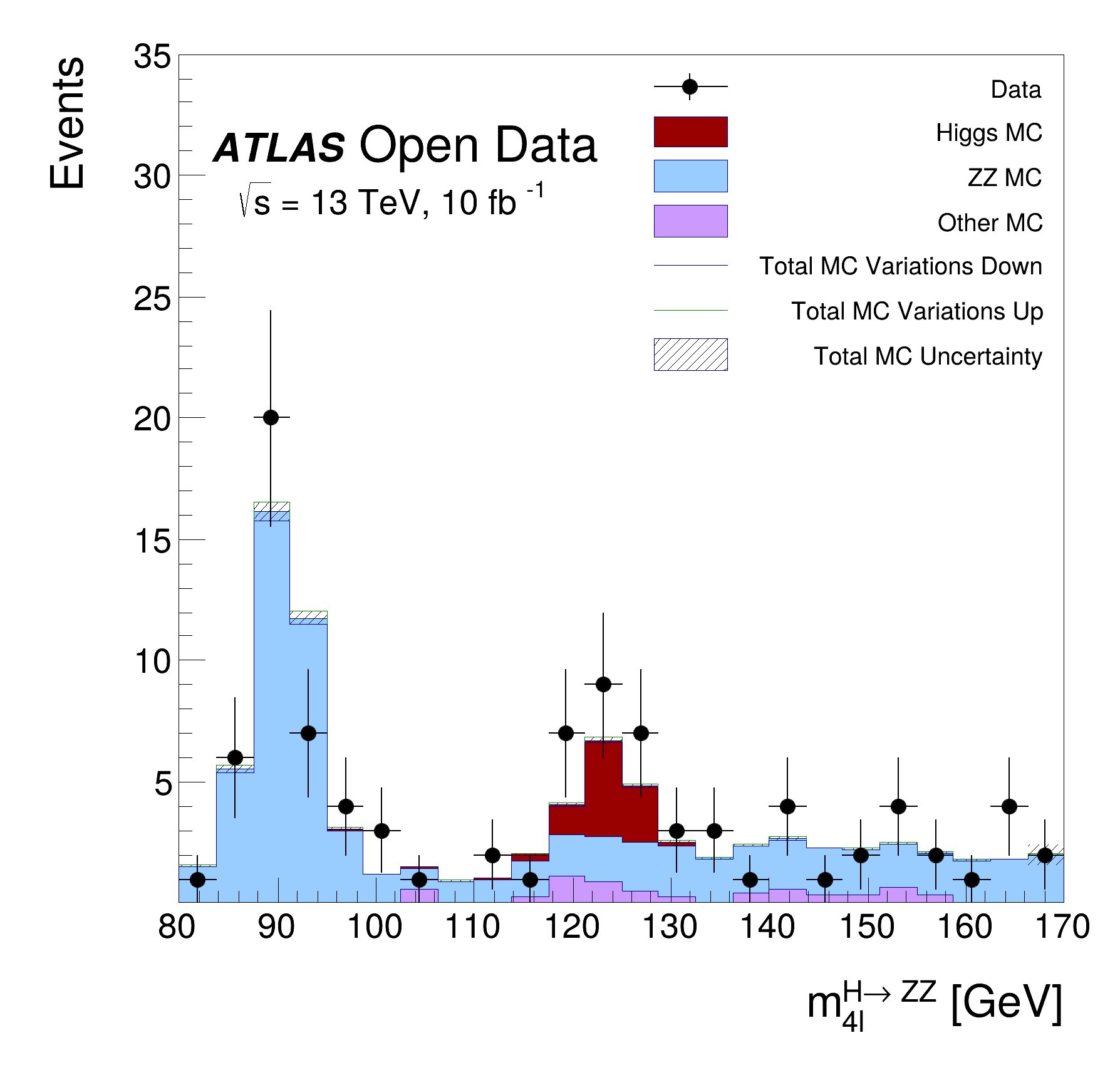
This tutorial is the Higgs to four lepton analysis from the ATLAS Open Data release in 2020 (http://opendata.atlas.cern/release/2020/documentation/). The data was taken with the ATLAS detector during 2016 at a center-of-mass energy of 13 TeV. The decay of the Standard Model Higgs boson to two Z bosons and subsequently to four leptons is called the "golden channel". The selection leads to a narrow invariant mass peak on top a relatively smooth and small background, revealing the Higgs at 125 GeV. The analysis is translated to an RDataFrame workflow processing about 300 MB of simulated events and data.
Lepton selection efficiency corrections ("scale factors") are applied to simulated samples to correct for the differences in the trigger, reconstruction, and identification efficiencies in simulation compared to real data. Systematic uncertainties for those scale factors are evaluated and the Vary function of RDataFrame is used to propagate the variations to the final four leptons mass distribution.
{
for (
size_t i = 0; i <
type.size(); i++) {
abs(z0[i] * sin(
p.Theta())) > 0.5)
return false;
} else {
return false;
}
}
return true;
}
{
}
void df106_HiggsToFourLeptons()
{
std::string
dataset_spec =
gROOT->GetTutorialsDir() + std::string(
"/analysis/dataframe/df106_HiggsToFourLeptons_spec.json");
#ifndef __CLING__
"using ROOT::RVecF;"
"bool GoodElectronsAndMuons(const ROOT::RVecI &type, const RVecF &pt, const RVecF &eta, const RVecF &phi, const RVecF &e,"
"const RVecF &trackd0pv, const RVecF &tracksigd0pv, const RVecF &z0);"
"float ComputeInvariantMass(const RVecF &pt, const RVecF &eta, const RVecF &phi, const RVecF &e);"
);
#endif
.DefinePerSample(
"lumi", [](
unsigned int slot,
const RSampleInfo &
id) {
return id.GetD(
"lumi"); })
.DefinePerSample(
"sumws", [](
unsigned int slot,
const RSampleInfo &
id) {
return id.GetD(
"sumws"); })
.DefinePerSample("sample_category",
[](
unsigned int slot,
const RSampleInfo &
id) {
return id.GetS(
"sample_category"); })
.DefinePerSample("scale",
return id.Contains("mc_363490.llll.4lep.root") ? 1.3f : 1.0f;
})
.Define("good_lep",
"abs(lep_eta) < 2.5 && lep_pt > 5000 && lep_ptcone30 / lep_pt < 0.3 && lep_etcone20 / lep_pt < 0.3")
.Filter("Sum(good_lep) == 4")
.Filter("Sum(lep_charge[good_lep]) == 0")
.Define("goodlep_sumtypes", "Sum(lep_type[good_lep])")
.Filter("goodlep_sumtypes == 44 || goodlep_sumtypes == 52 || goodlep_sumtypes == 48")
.Filter(
"GoodElectronsAndMuons(lep_type[good_lep], lep_pt[good_lep], lep_eta[good_lep], lep_phi[good_lep], "
"lep_E[good_lep], lep_trackd0pvunbiased[good_lep], lep_tracksigd0pvunbiased[good_lep], lep_z0[good_lep])")
.Define("goodlep_pt", "lep_pt[good_lep]")
.Define("goodlep_eta", "lep_eta[good_lep]")
.Define("goodlep_phi", "lep_phi[good_lep]")
.Define("goodlep_E", "lep_E[good_lep]")
.Define("goodlep_type", "lep_type[good_lep]")
.Filter("goodlep_pt[0] > 25000 && goodlep_pt[1] > 15000 && goodlep_pt[2] > 10000")
.Define("m4l", "ComputeInvariantMass(goodlep_pt, goodlep_eta, goodlep_phi, goodlep_E)")
.DefinePerSample(
"reweighting", [](
unsigned int slot,
const RSampleInfo &
id) {
return id.Contains(
"mc"); });
.Define("weight", ("scaleFactor_ELE * scaleFactor_MUON * scaleFactor_LepTRIGGER * "
"scaleFactor_PILEUP * mcWeight * scale * xsecs / sumws * lumi"));
auto df_zz =
df_mc.Filter(
"sample_category == \"zz\"")
.Filter("sample_category == \"data\"")
.Define("weight_", []() { return 1; })
const std::vector<double>
x{5.50e3, 5.52e3, 12.54e3, 17.43e3, 22.40e3, 27.48e3, 30
e3, 10000
e3};
const std::vector<double>
y{0.06628, 0.06395, 0.06396, 0.03372, 0.02441, 0.01403, 0, 0};
.Vary("weight",
const auto v =
Mean(
Map(
pt[
type == 11], [&graph](
auto p) {
return graph.Eval(
p); }));
},
{"weight", "goodlep_pt", "goodlep_type"}, {"up", "down"})
for (
unsigned int i = 0; i <
histos_mc[
"nominal"].GetXaxis()->GetNbins(); i++) {
}
gROOT->SetStyle(
"ATLAS");
auto c =
new TCanvas(
"c",
" ", 600, 600);
auto pad =
new TPad(
"upper_pad",
"", 0, 0, 1, 1);
auto stack =
new THStack(
"stack",
"");
stack->Draw("HIST");
stack->GetHistogram()->SetTitle("");
stack->GetHistogram()->GetXaxis()->SetLabelSize(0.035);
stack->GetHistogram()->GetXaxis()->SetTitleSize(0.045);
stack->GetHistogram()->GetXaxis()->SetTitleOffset(1.3);
stack->GetHistogram()->GetXaxis()->SetTitle("m_{4l}^{H#rightarrow ZZ} [GeV]");
stack->GetHistogram()->GetYaxis()->SetLabelSize(0.035);
stack->GetHistogram()->GetYaxis()->SetTitleSize(0.045);
stack->GetHistogram()->GetYaxis()->SetTitle("Events");
stack->SetMaximum(35);
stack->GetHistogram()->GetYaxis()->ChangeLabel(1, -1, 0);
data_label.DrawLatexNDC(0.19 + 0.13, 0.85,
"Open Data");
header.
DrawLatexNDC(0.21, 0.8,
"#sqrt{s} = 13 TeV, 10 fb^{-1}");
c->
SaveAs(
"df106_HiggsToFourLeptons_cpp.png");
std::cout << "Saved figure to df106_HiggsToFourLeptons_cpp.png" << std::endl;
}
{
df106_HiggsToFourLeptons();
}
ROOT::Detail::TRangeCast< T, true > TRangeDynCast
TRangeDynCast is an adapter class that allows the typed iteration through a TCollection.
winID h TVirtualViewer3D TVirtualGLPainter p
Option_t Option_t TPoint TPoint const char GetTextMagnitude GetFillStyle GetLineColor GetLineWidth GetMarkerStyle GetTextAlign GetTextColor GetTextSize void char Point_t Rectangle_t WindowAttributes_t Float_t Float_t Float_t Int_t Int_t UInt_t UInt_t Rectangle_t Int_t Int_t Window_t TString Int_t GCValues_t GetPrimarySelectionOwner GetDisplay GetScreen GetColormap GetNativeEvent const char const char dpyName wid window const char font_name cursor keysym reg const char only_if_exist regb h Point_t winding char text const char depth char const char Int_t count const char ColorStruct_t color const char Pixmap_t Pixmap_t PictureAttributes_t attr const char char ret_data h unsigned char height h Atom_t Int_t ULong_t ULong_t unsigned char prop_list Atom_t Atom_t Atom_t Time_t type
Class describing a generic LorentzVector in the 4D space-time, using the specified coordinate system ...
This type represents a sample identifier, to be used in conjunction with RDataFrame features such as ...
ROOT's RDataFrame offers a modern, high-level interface for analysis of data stored in TTree ,...
virtual void SetTextSize(Float_t tsize=1)
Set the text size.
A TGraph is an object made of two arrays X and Y with npoints each.
TH1 is the base class of all histogram classes in ROOT.
virtual Bool_t Add(TF1 *h1, Double_t c1=1, Option_t *option="")
Performs the operation: this = this + c1*f1 if errors are defined (see TH1::Sumw2),...
The Histogram stack class.
To draw Mathematical Formula.
TLatex * DrawLatexNDC(Double_t x, Double_t y, const char *text)
Draw this TLatex with new coordinates in NDC.
This class displays a legend box (TPaveText) containing several legend entries.
virtual void SaveAs(const char *filename="", Option_t *option="") const
Save this object in the file specified by filename.
The most important graphics class in the ROOT system.
auto Map(Args &&... args)
Create new collection applying a callable to the elements of the input collection.
RVec< T > Filter(const RVec< T > &v, F &&f)
Create a new collection with the elements passing the filter expressed by the predicate.
ROOT::RDataFrame FromSpec(const std::string &jsonFile)
Factory method to create an RDataFrame from a JSON specification file.
RResultMap< T > VariationsFor(RResultPtr< T > resPtr)
Produce all required systematic variations for the given result.
void AddProgressBar(ROOT::RDF::RNode df)
Add ProgressBar to a ROOT::RDF::RNode.
void EnableImplicitMT(UInt_t numthreads=0)
Enable ROOT's implicit multi-threading for all objects and methods that provide an internal paralleli...
Double_t Mean(Long64_t n, const T *a, const Double_t *w=nullptr)
Returns the weighted mean of an array a with length n.
A struct which stores some basic parameters of a TH1D.