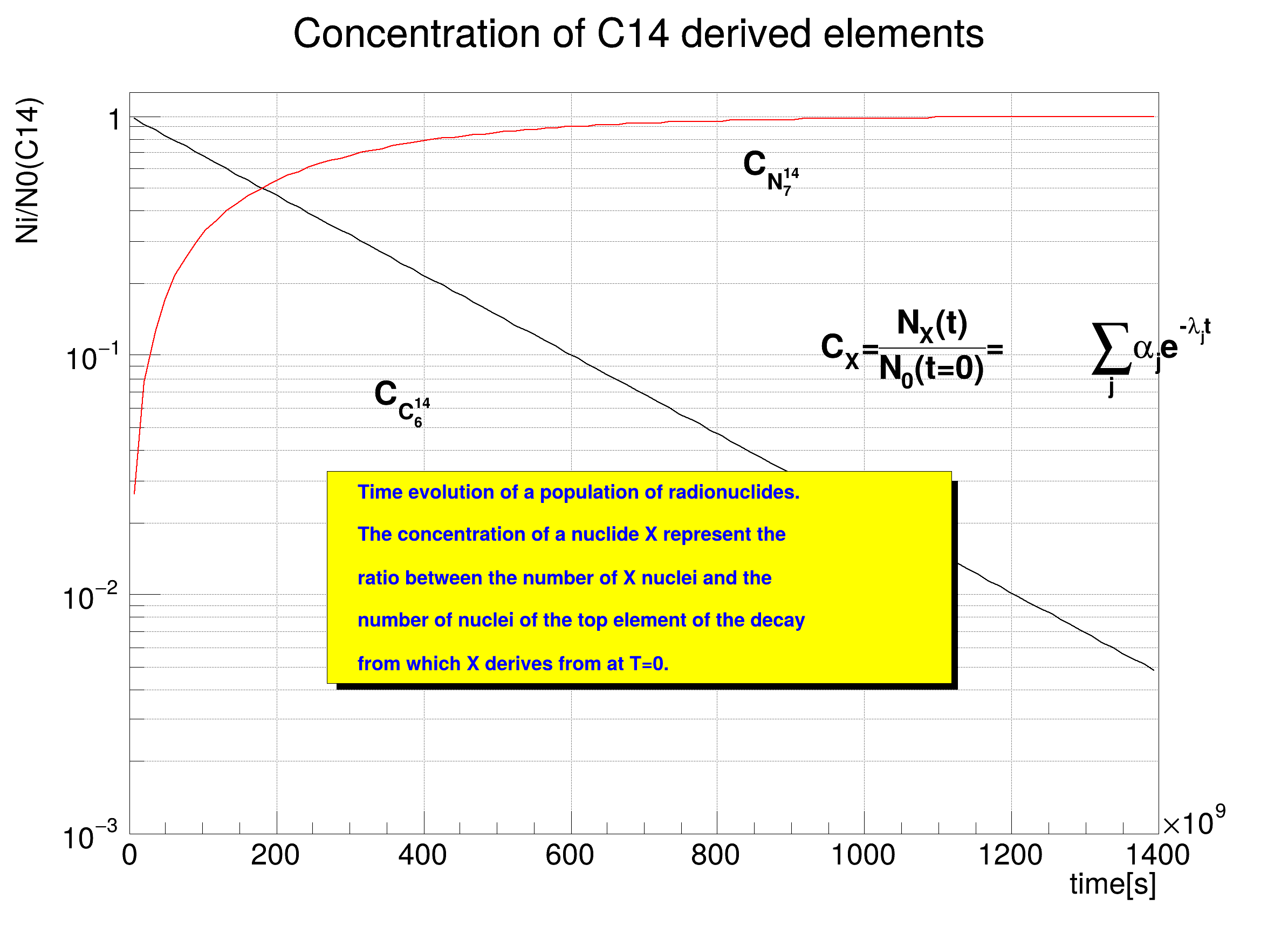
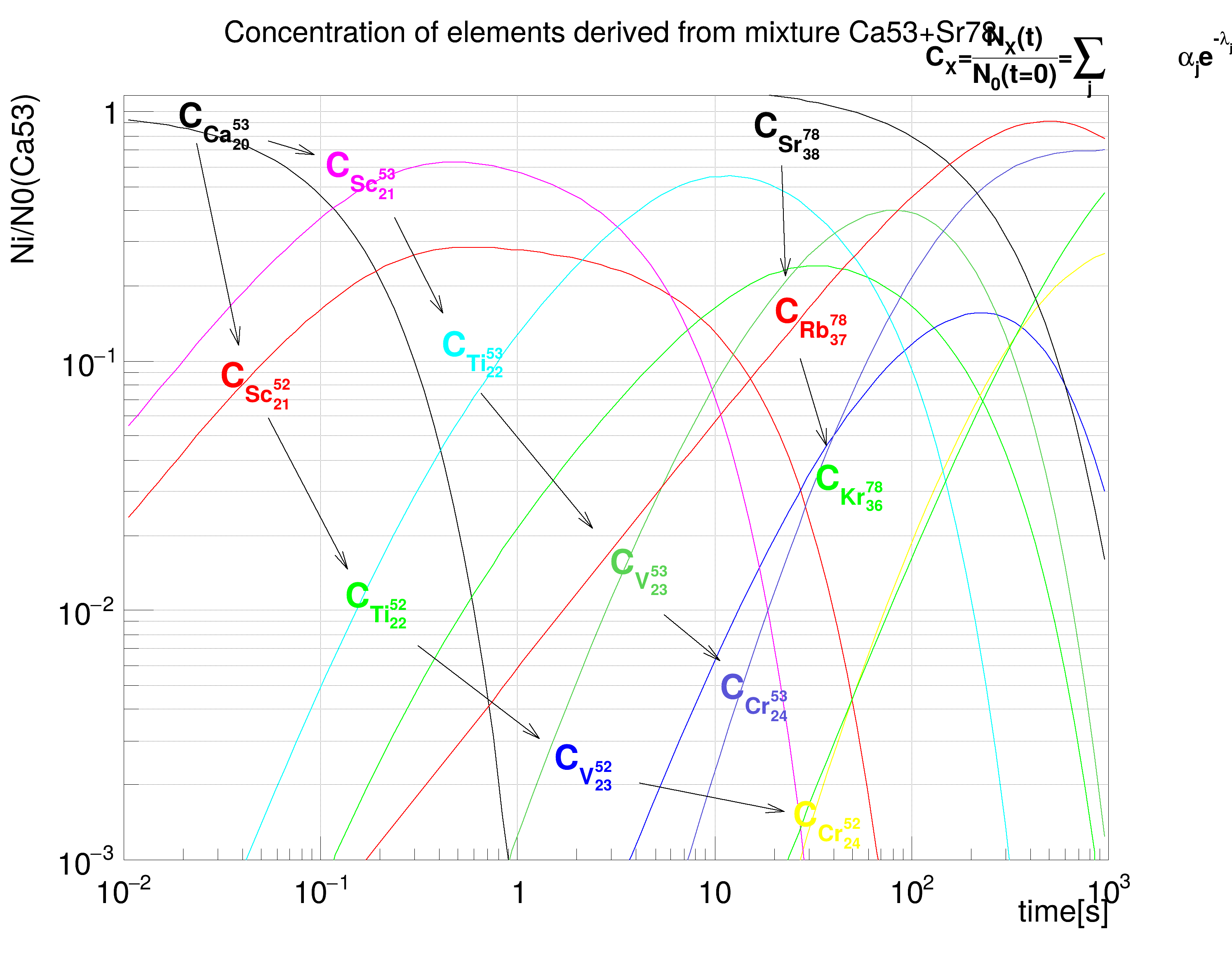
Macro that demonstrates usage of radioactive elements/materials/mixtures with TGeo package.
The isomeric number is optional and the default value is 0.
To create a radioactive material based on a radionuclide, one should use the constructor:
To create a radioactive mixture, one can use radionuclides as well as stable elements:
Once defined, one can retrieve the time evolution for the radioactive materials/mixtures by using one of the 2 methods:
All radionuclides in the output population list have attached objects that represent the time evolution of their fraction of nuclei with respect to the top radionuclide in the decay chain. These objects (Bateman solutions) can be retrieved and drawn:
Another method allows to create the evolution of a given radioactive material/mixture at a given moment in time:
The method will create the mixture that result from the decay of a initial material/mixture at TIME, while all resulting elements having a fractional weight less than PRECISION are excluded.
{
printf(
"___________________________________________________________\n");
printf(
"Radioactive material:\n");
printf(
"Radioactive material evolution after %g years:\n", time/3.1536e7);
printf(
"___________________________________________________________\n");
printf(
"Radioactive mixture:\n");
time = 1000.;
printf(
"Radioactive mixture evolution after %g seconds:\n", time);
tex->SetTextSize(0.0388601);
tex =
new TLatex(3.33e11,0.0620678,
"C_{C^{14}_{6}}");
tex->SetTextSize(0.0388601);
tex =
new TLatex(9.4e11,0.098,
"C_{X}=#frac{N_{X}(t)}{N_{0}(t=0)}=\
#sum_{j}#alpha_{j}e^{-#lambda_{j}t}");
tex->SetTextSize(0.0388601);
pt->
AddText(
"Time evolution of a population of radionuclides.");
pt->
AddText(
"The concentration of a nuclide X represent the ");
pt->
AddText(
"ratio between the number of X nuclei and the ");
pt->
AddText(
"number of nuclei of the top element of the decay");
pt->
AddText(
"from which X derives from at T=0. ");
tex =
new TLatex(0.019,0.861,
"C_{Ca^{53}_{20}}");
tex->SetTextSize(0.0388601);
tex =
new TLatex(0.0311,0.078064,
"C_{Sc^{52}_{21}}");
tex->SetTextSize(0.0388601);
tex =
new TLatex(0.1337,0.010208,
"C_{Ti^{52}_{22}}");
tex->SetTextSize(0.0388601);
tex =
new TLatex(1.54158,0.00229644,
"C_{V^{52}_{23}}");
tex->SetTextSize(0.0388601);
tex =
new TLatex(25.0522,0.00135315,
"C_{Cr^{52}_{24}}");
tex->SetTextSize(0.0388601);
tex =
new TLatex(0.1056,0.5429,
"C_{Sc^{53}_{21}}");
tex->SetTextSize(0.0388601);
tex =
new TLatex(0.411,0.1044,
"C_{Ti^{53}_{22}}");
tex->SetTextSize(0.0388601);
tex =
new TLatex(2.93358,0.0139452,
"C_{V^{53}_{23}}");
tex->SetTextSize(0.0388601);
tex =
new TLatex(10.6235,0.00440327,
"C_{Cr^{53}_{24}}");
tex->SetTextSize(0.0388601);
tex =
new TLatex(15.6288,0.782976,
"C_{Sr^{78}_{38}}");
tex->SetTextSize(0.0388601);
tex =
new TLatex(20.2162,0.141779,
"C_{Rb^{78}_{37}}");
tex->SetTextSize(0.0388601);
tex =
new TLatex(32.4055,0.0302101,
"C_{Kr^{78}_{36}}");
tex->SetTextSize(0.0388601);
tex =
new TLatex(117.,1.52,
"C_{X}=#frac{N_{X}(t)}{N_{0}(t=0)}=#sum_{j}\
#alpha_{j}e^{-#lambda_{j}t}");
arrow->SetFillStyle(1001);
arrow =
new TArrow(0.0543138,0.0586338,0.136594,0.0146596,0.02,
">");
arrow->SetFillStyle(1001);
arrow =
new TArrow(0.31528,0.00722919,1.29852,0.00306079,0.02,
">");
arrow->SetFillStyle(1001);
arrow =
new TArrow(4.13457,0.00201942,22.5047,0.00155182,0.02,
">");
arrow->SetFillStyle(1001);
arrow =
new TArrow(0.0543138,0.761893,0.0928479,0.67253,0.02,
">");
arrow->SetFillStyle(1001);
arrow =
new TArrow(0.238566,0.375717,0.416662,0.154727,0.02,
">");
arrow->SetFillStyle(1001);
arrow =
new TArrow(0.653714,0.074215,2.41863,0.0213142,0.02,
">");
arrow->SetFillStyle(1001);
arrow =
new TArrow(5.58256,0.00953882,10.6235,0.00629343,0.02,
">");
arrow->SetFillStyle(1001);
arrow =
new TArrow(22.0271,0.601935,22.9926,0.218812,0.02,
">");
arrow->SetFillStyle(1001);
arrow =
new TArrow(27.2962,0.102084,36.8557,0.045686,0.02,
">");
arrow->SetFillStyle(1001);
}
{
if (logx)
can->SetLogx();
if (!
el->IsRadioNuclide())
continue;
sol->SetLineColor(1+(i%9));
if (i==0) {
Form(
"conc%s",
sol->GetElement()->GetName()));
if (func) {
"Concentration of C14 derived elements;time[s];Ni/N0(C14)");
"Concentration of elements derived from mixture Ca53+Sr78;\
time[s];Ni/N0(Ca53)");
}
}
}
}
}
ROOT::Detail::TRangeCast< T, true > TRangeDynCast
TRangeDynCast is an adapter class that allows the typed iteration through a TCollection.
R__EXTERN TGeoManager * gGeoManager
char * Form(const char *fmt,...)
Formats a string in a circular formatting buffer.
Draw all kinds of Arrows.
virtual void SetFillColor(Color_t fcolor)
Set the fill area color.
virtual void SetTextAlign(Short_t align=11)
Set the text alignment.
virtual void SetTextColor(Color_t tcolor=1)
Set the text color.
void SetTitle(const char *title="") override
Set function title if title has the form "fffffff;xxxx;yyyy", it is assumed that the function title i...
The manager class for any TGeo geometry.
TGeoElementTable * GetElementTable()
Returns material table. Creates it if not existing.
To draw Mathematical Formula.
A Pave (see TPave) with text, lines or/and boxes inside.
virtual TText * AddText(Double_t x1, Double_t y1, const char *label)
Add a new Text line to this pavetext at given coordinates.
void Draw(Option_t *option="") override
Draw this pavetext with its current attributes.