ROOT::Math::KelvinFunctions Class Reference

This class calculates the Kelvin functions Ber(x), Bei(x), Ker(x), Kei(x), and their first derivatives.

Definition at line 38 of file KelvinFunctions.h.

Public Member Functions
virtual	~KelvinFunctions ()

Static Public Member Functions
static double	Bei (double x)
static double	Ber (double x)
static double	DBei (double x)
	Calculates the first derivative of Bei(x). More...
static double	DBer (double x)
	Calculates the first derivative of Ber(x). More...
static double	DKei (double x)
	Calculates the first derivative of Kei(x). More...
static double	DKer (double x)
	Calculates the first derivative of Ker(x). More...
static double	F1 (double x)
	Utility function appearing in the calculations of the Kelvin functions Bei(x) and Ber(x) (and their derivatives). More...
static double	F2 (double x)
	Utility function appearing in the calculations of the Kelvin functions Kei(x) and Ker(x) (and their derivatives). More...
static double	G1 (double x)
	Utility function appearing in the calculations of the Kelvin functions Bei(x) and Ber(x) (and their derivatives). More...
static double	G2 (double x)
	Utility function appearing in the calculations of the Kelvin functions Kei(x) and Ker(x) (and their derivatives). More...
static double	Kei (double x)
static double	Ker (double x)
static double	M (double x)
	Utility function appearing in the asymptotic expansions of DBer(x) and DBei(x). More...
static double	N (double x)
	Utility function appearing in the asymptotic expansions of DKer(x) and DKei(x). More...
static double	Phi (double x)
	Utility function appearing in the asymptotic expansions of DKer(x) and DKei(x). More...
static double	Theta (double x)
	Utility function appearing in the asymptotic expansions of DBer(x) and DBei(x). More...

Static Protected Attributes
static double	fgEpsilon = 1.e-20
static double	fgMin = 20

#include <Math/KelvinFunctions.h>

Constructor & Destructor Documentation

~KelvinFunctions()

virtual ROOT::Math::KelvinFunctions::~KelvinFunctions ( )

inlinevirtual

Definition at line 63 of file KelvinFunctions.h.

Member Function Documentation

Bei()

double ROOT::Math::KelvinFunctions::Bei ( double  x )

static

$$Bei(x) = Bei_{0}(x) = Im\left[J_{0}\left(x e^{3\pi i/4}\right)\right]$$

where x is real, and $J_{0}(z)$ is the zeroth-order Bessel function of the first kind.

If x < fgMin (=20), Bei(x) is computed according to its polynomial approximation

$$Bei(x) = \sum_{n \geq 0}\frac{(-1)^{n}(x/2)^{4n+2}}{[(2n+1)!]^{2}}$$

For x > fgMin, Bei(x) is computed according to its asymptotic expansion:

$$Bei(x) = \frac{e^{x/\sqrt{2}}}{\sqrt{2\pi x}} [F1(x) sin\alpha + G1(x) cos\alpha] - \frac{1}{\pi}Ker(x)$$

where $\alpha = \frac{x}{\sqrt{2}} - \frac{\pi}{8}$.

See also F1() and G1().

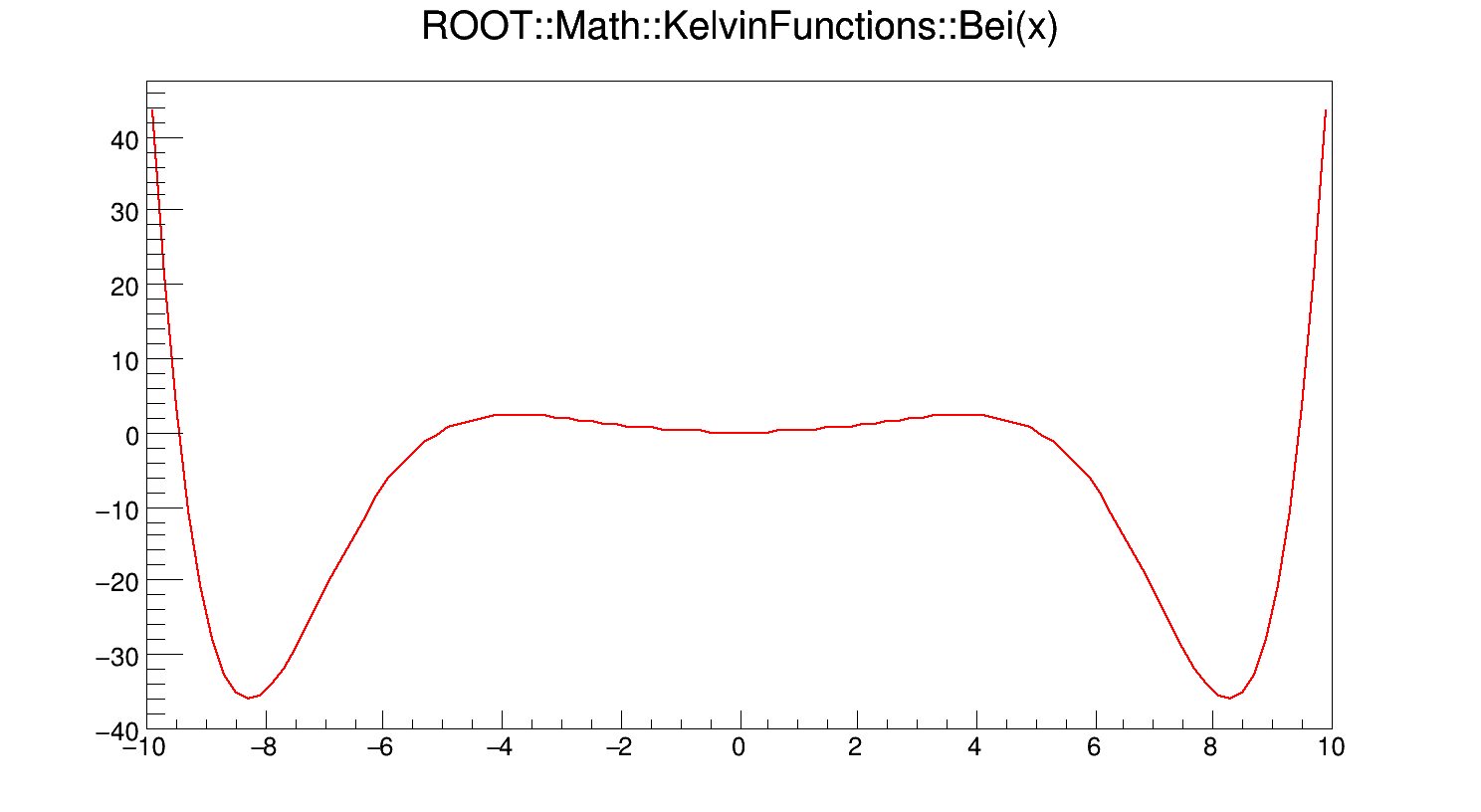
Definition at line 130 of file KelvinFunctions.cxx.

Ber()

double ROOT::Math::KelvinFunctions::Ber ( double  x )

static

$$Ber(x) = Ber_{0}(x) = Re\left[J_{0}\left(x e^{3\pi i/4}\right)\right]$$

where x is real, and $J_{0}(z)$ is the zeroth-order Bessel function of the first kind.

If x < fgMin (=20), Ber(x) is computed according to its polynomial approximation

$$Ber(x) = 1 + \sum_{n \geq 1}\frac{(-1)^{n}(x/2)^{4n}}{[(2n)!]^{2}}$$

For x > fgMin, Ber(x) is computed according to its asymptotic expansion:

$$Ber(x) = \frac{e^{x/\sqrt{2}}}{\sqrt{2\pi x}} [F1(x) cos\alpha + G1(x) sin\alpha] - \frac{1}{\pi}Kei(x)$$

where $\alpha = \frac{x}{\sqrt{2}} - \frac{\pi}{8}$.

See also F1() and G1().

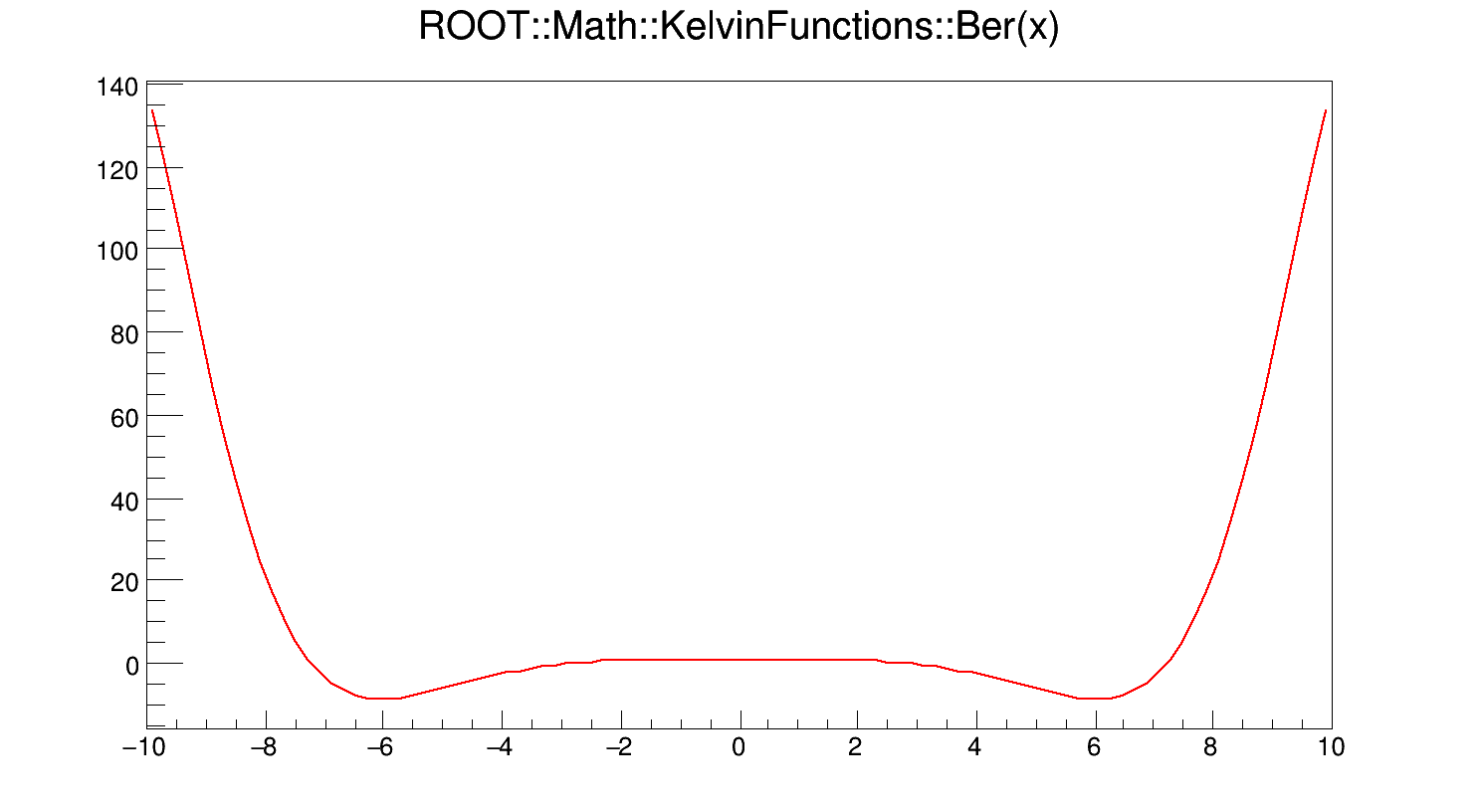
Definition at line 72 of file KelvinFunctions.cxx.

DBei()

double ROOT::Math::KelvinFunctions::DBei ( double  x )

static

Calculates the first derivative of Bei(x).

If x < fgMin (=20), DBei(x) is computed according to the derivative of the polynomial approximation of Bei(x). Otherwise it is computed according to its asymptotic expansion

$$\frac{d}{dx} Bei(x) = M sin\left(\theta - \frac{\pi}{4}\right)$$

See also M() and Theta().

Definition at line 359 of file KelvinFunctions.cxx.

DBer()

double ROOT::Math::KelvinFunctions::DBer ( double  x )

static

Calculates the first derivative of Ber(x).

If x < fgMin (=20), DBer(x) is computed according to the derivative of the polynomial approximation of Ber(x). Otherwise it is computed according to its asymptotic expansion

$$\frac{d}{dx} Ber(x) = M cos\left(\theta - \frac{\pi}{4}\right)$$

See also M() and Theta().

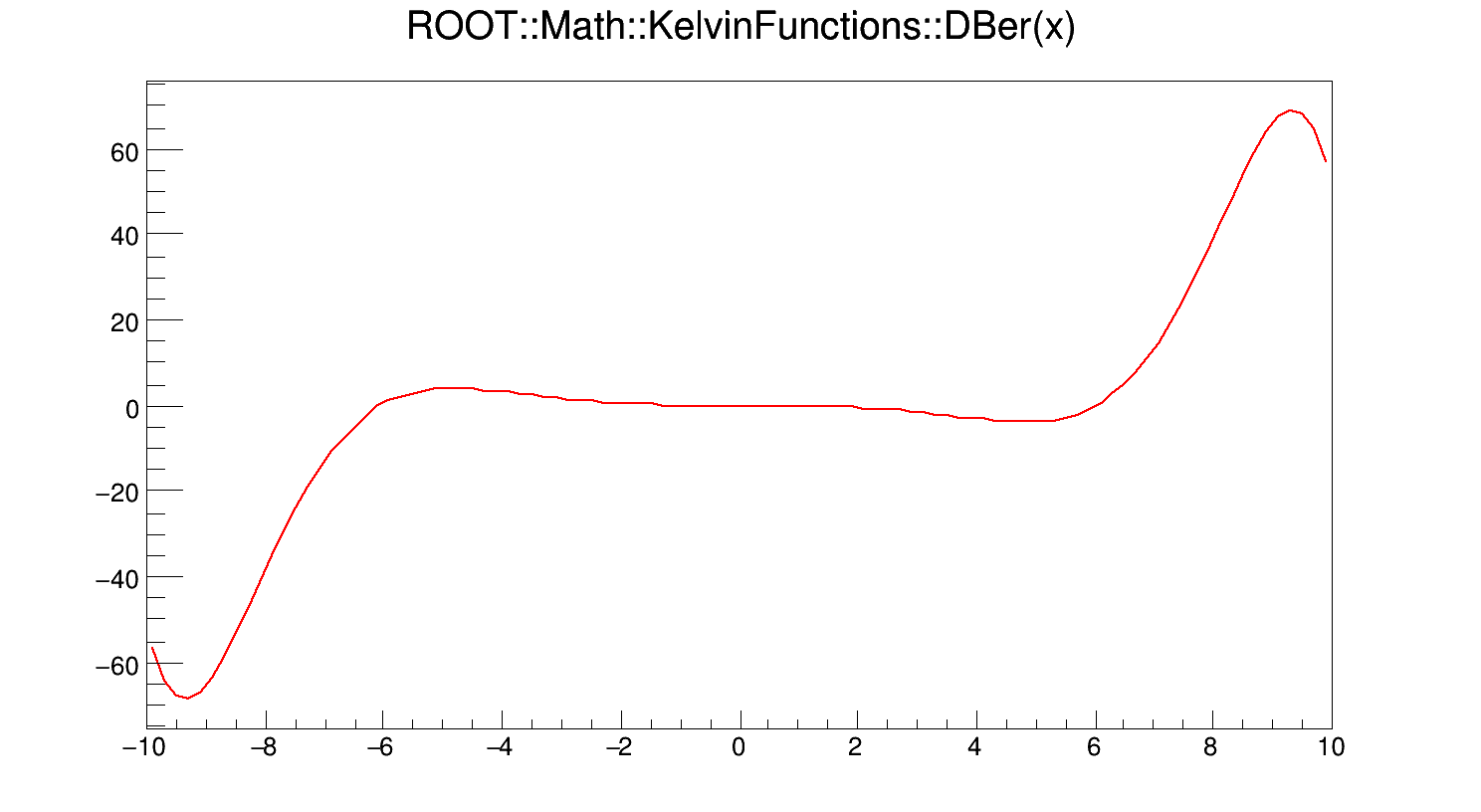
Definition at line 314 of file KelvinFunctions.cxx.

DKei()

double ROOT::Math::KelvinFunctions::DKei ( double  x )

static

Calculates the first derivative of Kei(x).

If x < fgMin (=20), DKei(x) is computed according to the derivative of the polynomial approximation of Kei(x). Otherwise it is computed according to its asymptotic expansion

$$\frac{d}{dx} Kei(x) = N sin\left(\phi - \frac{\pi}{4}\right)$$

See also N() and Phi().

Definition at line 452 of file KelvinFunctions.cxx.

DKer()

double ROOT::Math::KelvinFunctions::DKer ( double  x )

static

Calculates the first derivative of Ker(x).

If x < fgMin (=20), DKer(x) is computed according to the derivative of the polynomial approximation of Ker(x). Otherwise it is computed according to its asymptotic expansion

$$\frac{d}{dx} Ker(x) = N cos\left(\phi - \frac{\pi}{4}\right)$$

See also N() and Phi().

Definition at line 404 of file KelvinFunctions.cxx.

F1()

double ROOT::Math::KelvinFunctions::F1 ( double  x )

static

Utility function appearing in the calculations of the Kelvin functions Bei(x) and Ber(x) (and their derivatives).

F1(x) is given by

$$F1(x) = 1 + \sum_{n \geq 1} \frac{\prod_{m=1}^{n}(2m - 1)^{2}}{n! (8x)^{n}} cos\left(\frac{n\pi}{4}\right)$$

Definition at line 487 of file KelvinFunctions.cxx.

F2()

double ROOT::Math::KelvinFunctions::F2 ( double  x )

static

Utility function appearing in the calculations of the Kelvin functions Kei(x) and Ker(x) (and their derivatives).

F2(x) is given by

$$F2(x) = 1 + \sum_{n \geq 1} (-1)^{n} \frac{\prod_{m=1}^{n}(2m - 1)^{2}}{n! (8x)^{n}} cos\left(\frac{n\pi}{4}\right)$$

Definition at line 516 of file KelvinFunctions.cxx.

G1()

double ROOT::Math::KelvinFunctions::G1 ( double  x )

static

Utility function appearing in the calculations of the Kelvin functions Bei(x) and Ber(x) (and their derivatives).

G1(x) is given by

$$G1(x) = \sum_{n \geq 1} \frac{\prod_{m=1}^{n}(2m - 1)^{2}}{n! (8x)^{n}} sin\left(\frac{n\pi}{4}\right)$$

Definition at line 547 of file KelvinFunctions.cxx.

G2()

double ROOT::Math::KelvinFunctions::G2 ( double  x )

static

Utility function appearing in the calculations of the Kelvin functions Kei(x) and Ker(x) (and their derivatives).

G2(x) is given by

$$G2(x) = \sum_{n \geq 1} (-1)^{n} \frac{\prod_{m=1}^{n}(2m - 1)^{2}}{n! (8x)^{n}} sin\left(\frac{n\pi}{4}\right)$$

Definition at line 574 of file KelvinFunctions.cxx.

Kei()

double ROOT::Math::KelvinFunctions::Kei ( double  x )

static

$$Kei(x) = Kei_{0}(x) = Im\left[K_{0}\left(x e^{3\pi i/4}\right)\right]$$

where x is real, and $K_{0}(z)$ is the zeroth-order modified Bessel function of the second kind.

If x < fgMin (=20), Kei(x) is computed according to its polynomial approximation

$$Kei(x) = -\left(ln \frac{x}{2} + \gamma\right) Bei(x) - \left(\frac{\pi}{4} - \delta\right) Ber(x) + \sum_{n \geq 0} \frac{(-1)^{n}}{[(2n)!]^{2}} H_{2n} \left(\frac{x}{2}\right)^{4n+2}$$

where $\gamma = 0.577215664...$ is the Euler-Mascheroni constant, $\delta = \pi$ for x < 0 and is otherwise zero, and

$$H_{n} = \sum_{k = 1}^{n} \frac{1}{k}$$

For x > fgMin, Kei(x) is computed according to its asymptotic expansion:

$$Kei(x) = - \sqrt{\frac{\pi}{2x}} e^{-x/\sqrt{2}} [F2(x) sin\beta + G2(x) cos\beta]$$

where $\beta = \frac{x}{\sqrt{2}} + \frac{\pi}{8}$.

See also F2() and G2().

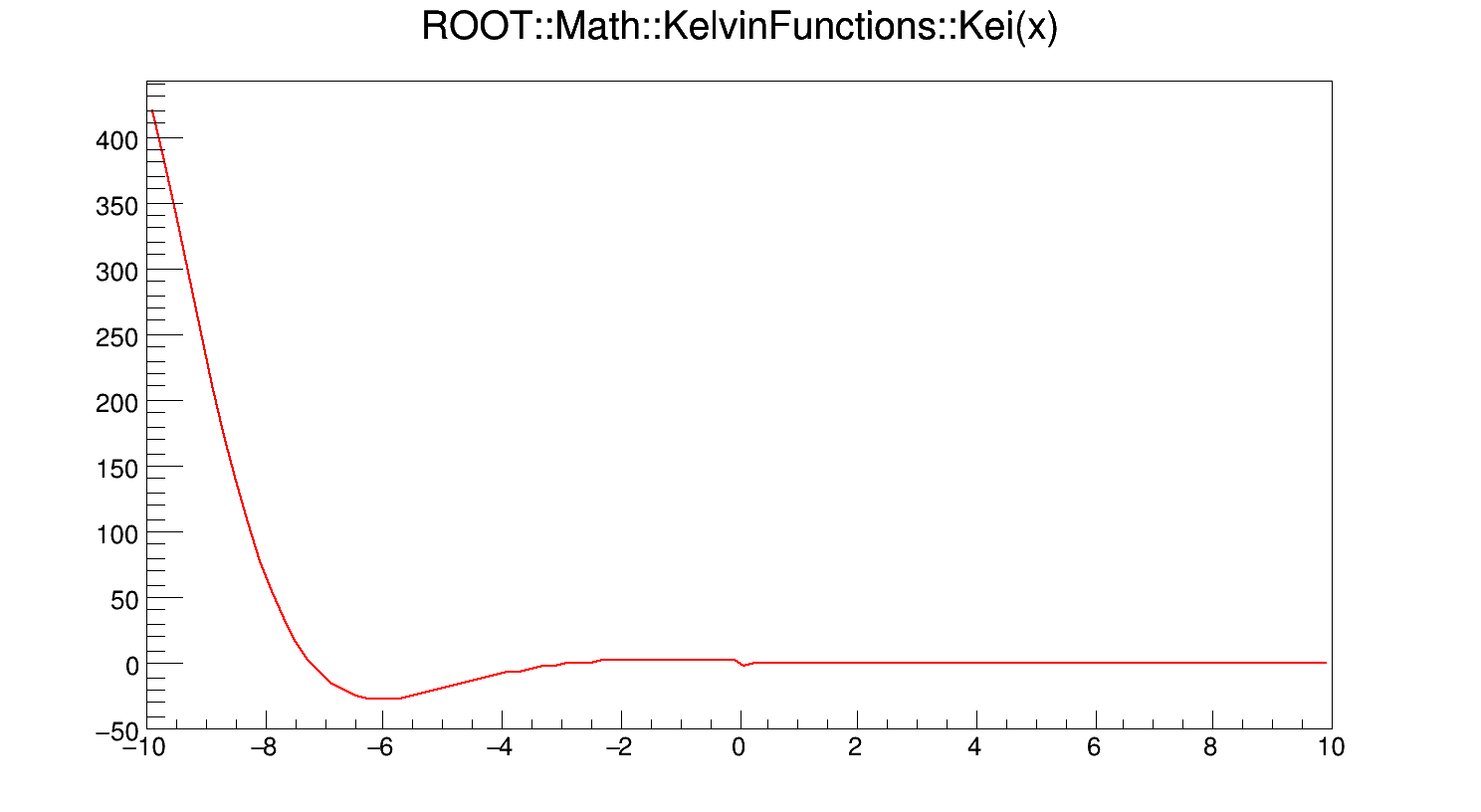
Definition at line 262 of file KelvinFunctions.cxx.

Ker()

double ROOT::Math::KelvinFunctions::Ker ( double  x )

static

$$Ker(x) = Ker_{0}(x) = Re\left[K_{0}\left(x e^{3\pi i/4}\right)\right]$$

where x is real, and $K_{0}(z)$ is the zeroth-order modified Bessel function of the second kind.

If x < fgMin (=20), Ker(x) is computed according to its polynomial approximation

$$Ker(x) = -\left(ln \frac{|x|}{2} + \gamma\right) Ber(x) + \left(\frac{\pi}{4} - \delta\right) Bei(x) + \sum_{n \geq 0} \frac{(-1)^{n}}{[(2n)!]^{2}} H_{2n} \left(\frac{x}{2}\right)^{4n}$$

where $\gamma = 0.577215664...$ is the Euler-Mascheroni constant, $\delta = \pi$ for x < 0 and is otherwise zero, and

$$H_{n} = \sum_{k = 1}^{n} \frac{1}{k}$$

For x > fgMin, Ker(x) is computed according to its asymptotic expansion:

$$Ker(x) = \sqrt{\frac{\pi}{2x}} e^{-x/\sqrt{2}} [F2(x) cos\beta + G2(x) sin\beta]$$

where $\beta = \frac{x}{\sqrt{2}} + \frac{\pi}{8}$.

See also F2() and G2().

Definition at line 195 of file KelvinFunctions.cxx.

M()

double ROOT::Math::KelvinFunctions::M ( double  x )

static

Utility function appearing in the asymptotic expansions of DBer(x) and DBei(x).

M(x) is given by

$$M(x) = \frac{e^{x/\sqrt{2}}}{\sqrt{2\pi x}}\left(1 + \frac{1}{8\sqrt{2} x} + \frac{1}{256 x^{2}} - \frac{399}{6144\sqrt{2} x^{3}} + O\left(\frac{1}{x^{4}}\right)\right)$$

Definition at line 603 of file KelvinFunctions.cxx.

N()

double ROOT::Math::KelvinFunctions::N ( double  x )

static

Utility function appearing in the asymptotic expansions of DKer(x) and DKei(x).

N(x) is given by

$$N(x) = \sqrt{\frac{\pi}{2x}} e^{-x/\sqrt{2}} \left(1 - \frac{1}{8\sqrt{2} x} + \frac{1}{256 x^{2}} + \frac{399}{6144\sqrt{2} x^{3}} + O\left(\frac{1}{x^{4}}\right)\right)$$

Definition at line 635 of file KelvinFunctions.cxx.

Phi()

double ROOT::Math::KelvinFunctions::Phi ( double  x )

static

Utility function appearing in the asymptotic expansions of DKer(x) and DKei(x).

$\phi(x)$ is given by

$$\phi(x) = - \frac{x}{\sqrt{2}} - \frac{\pi}{8} + \frac{1}{8\sqrt{2} x} - \frac{1}{16 x^{2}} + \frac{25}{384\sqrt{2} x^{3}} + O\left(\frac{1}{x^{5}}\right)$$

Definition at line 651 of file KelvinFunctions.cxx.

Theta()

double ROOT::Math::KelvinFunctions::Theta ( double  x )

static

Utility function appearing in the asymptotic expansions of DBer(x) and DBei(x).

$\theta(x)$ is given by

$$\theta(x) = \frac{x}{\sqrt{2}} - \frac{\pi}{8} - \frac{1}{8\sqrt{2} x} - \frac{1}{16 x^{2}} - \frac{25}{384\sqrt{2} x^{3}} + O\left(\frac{1}{x^{5}}\right)$$

Definition at line 619 of file KelvinFunctions.cxx.

Member Data Documentation

fgEpsilon

double ROOT::Math::KelvinFunctions::fgEpsilon = 1.e-20

staticprotected

Definition at line 68 of file KelvinFunctions.h.

fgMin

double ROOT::Math::KelvinFunctions::fgMin = 20

staticprotected

Definition at line 67 of file KelvinFunctions.h.

---

The documentation for this class was generated from the following files:

• math/mathmore/inc/Math/KelvinFunctions.h
• math/mathmore/src/KelvinFunctions.cxx