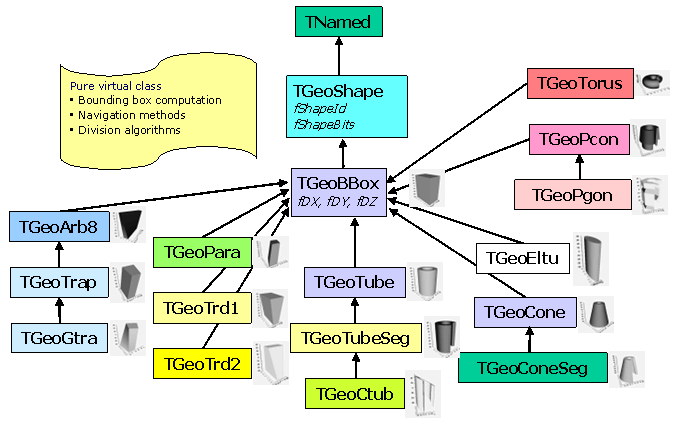
Shapes are geometrical objects that provide the basic modeling functionality.
The "shapes" provide the definition of the local coordinate system of the volume. Any volume must have a shape. Any shape recognized by the modeller has to derive from the base **TGeoShape** class, providing methods for:
All the features above are globally managed by the modeller in order to provide navigation functionality. In addition to those, shapes have also to implement additional specific abstract methods:
The modeller currently provides a set of 20 basic shapes, which we will call primitives. It also provides a special class allowing the creation of shapes as a result of Boolean operations between primitives. These are called composite shapes and the composition operation can be recursive (combined composites). This allows the creation of a quite large number of different shape topologies and combinations. You can have a look and run the tutorial: geodemo.C
Shapes are named objects and all primitives have constructors like:
Naming shape primitive is mandatory only for the primitives used in Boolean composites (see "Composite Shapes"). For the sake of simplicity, we will describe only the constructors in the second form.
Shapes are named objects and register themselves to the manager class at creation time. This is responsible for their final deletion. Shapes can be created without name if their retrieval by name is no needed. Generally shapes are objects that are useful only at geometry creation stage. The pointer to a shape is in fact needed only when referring to a given volume and it is always accessible at that level. Several volumes may reference a single shape; therefore its deletion is not possible once volumes were defined based on it.
The navigation features related for instance to tracking particles are performed in the following way: Each shape implement its specific algorithms for all required tasks in its local reference system. Note that the manager class handles global queries related to geometry. However, shape-related queries might be sometimes useful:
The method above returns kTRUE if the point *point is actually inside the shape. The point has to be defined in the local shape reference. For instance, for a box having DX,DY and DZhalf-lengths a point will be considered inside if:
-DX <= point[0] <= DX
-DY <= point[1] <= DY
-DZ <= point[2] <= DZ
The method computes the distance to exiting a shape from a given point inside, along a given direction. This direction is given by its director cosines with respect to the local shape coordinate system. This method provides additional information according the value of iact input parameter:
iact = 0computes only safe distance and fill it at the location given by SAFE;iact = 1a proposed STEP is supplied. The safe distance is computed first. If this is bigger than STEP than the proposed step is approved and returned by the method since it does not cross the shape boundaries. Otherwise, the distance to exiting the shape is computed and returned;iact = 2computes both safe distance and distance to exiting, ignoring the proposed step;iact > 2computes only the distance to exiting, ignoring anything elseThis method computes the distance to entering a shape from a given point outside. It acts in the same way as the previous method.
This computes the maximum shift of a point in any direction that does not change its inside/outsidestate (does not cross shape boundaries). The state of the point has to be properly supplied.
The method above computes the director cosines of normal to the crossed shape surface from a given point towards direction. This is filled into the norm array, supplied by the user. The normal vector is always chosen such that its dot product with the direction is positive defined.
Shape objects embeds only the minimum set of parameters that are fully describing a valid physical shape. For instance, the half-length, the minimum and maximum radius represent a tube. Shapes are used together with media in order to create volumes, which in their turn are the main components of the geometrical tree. A specific shape can be created stand-alone:
Sometimes it is much easier to create a volume having a given shape in one step, since shapes are not directly linked in the geometrical tree but volumes are:
Shapes can generally be divided along a given axis. Supported axes are: X, Y, Z, Rxy, Phi, Rxyz. A given shape cannot be divided however on any axis. The general rule is that that divisions are possible on whatever axis that produces still known shapes as slices. The division of shapes are performed by the call TGeoShape::Divide(), but this operation can be done only via TGeoVolume::Divide() method. In other words, the algorithm for dividing a specific shape is known by the shape object, but is always invoked in a generic way from the volume level. Details on how to do that can be found in the paragraph ‘Dividing volumes'. One can see how all division options are interpreted and which their result inside specific shape classes is.
Shapes generally have a set of parameters that is well defined at build time. In fact, when the final geometrical hierarchy is assembled and the geometry is closed, all constituent shapes MUST**have well defined and valid parameters. In order to ease-up geometry creation, some parameterizations are however allowed.
For instance let's suppose that we need to define several volumes having exactly the same properties but different sizes. A way to do this would be to create as many different volumes and shapes. The modeller allows however the definition of a single volume having undefined shape parameters.
name: the name of the newly created volume;shape:the type of the associated shape. This has to contain the case-insensitive first 4 letters of the corresponding class name (e.g. "`tubs`" will match **TGeoTubeSeg**, "`bbox`" will match **TGeoBBox**)nmed: the medium number.This will create a special volume that will not be directly used in the geometry, but whenever positioned will require a list of actual parameters for the current shape that will be created in this process. Such volumes having shape parameters known only when used have to be positioned only with **TGeoManager::Node() method (see ‘Creating and Positioning Volumes').**
Other case when shape parameterizations are quite useful is scaling geometry structures. Imagine that we would like to enlarge/shrink a detector structure on one or more axes. This happens quite often in real life and is handled by "fitting mother" parameters. This is accomplished by defining shapes with one or more invalid (negative) parameters. For instance, defining a box having dx=10., dy=10., and dz=-1 will not generate an error but will be interpreted in a different way: A special volume **TGeoVolumeMulti** will be created. Whenever positioned inside a mother volume, this will create a normal **TGeoVolume** object having as shape a box with dz fitting the corresponding dzof the mother shape. Generally, this type of parameterization is used when positioning volumes in containers having a matching shape, but it works also for most reasonable combinations.
Topics | |
| Tubes | |
| Cones | |
| Trapezoids | |
Classes | |
| class | TGeoBBox |
| Box class. More... | |
| class | TGeoCompositeShape |
| Composite shapes are Boolean combinations of two or more shape components. More... | |
| class | TGeoHalfSpace |
| A half space is limited just by a plane, defined by a point and the normal direction. More... | |
| class | TGeoHelix |
| Class representing a helix curve. More... | |
| class | TGeoHype |
| A hyperboloid is represented as a solid limited by two planes perpendicular to the Z axis (top and bottom planes) and two hyperbolic surfaces of revolution about Z axis (inner and outer surfaces). More... | |
| class | TGeoPara |
| Parallelepiped class. More... | |
| class | TGeoParaboloid |
| A paraboloid is defined by the revolution surface generated by a parabola and is bounded by two planes perpendicular to Z axis. More... | |
| class | TGeoPcon |
| A polycone is represented by a sequence of tubes/cones, glued together at defined Z planes. More... | |
| class | TGeoPgon |
| Polygons are defined in the same way as polycones, the difference being just that the segments between consecutive Z planes are regular polygons. More... | |
| class | TGeoPolygon |
| An arbitrary polygon defined by vertices. More... | |
| class | TGeoShape |
| Base abstract class for all shapes. More... | |
| class | TGeoShapeAssembly |
| The shape encapsulating an assembly (union) of volumes. More... | |
| class | TGeoSphere |
| TGeoSphere are not just balls having internal and external radii, but sectors of a sphere having defined theta and phi ranges. More... | |
| class | TGeoTorus |
| The torus is defined by its axial radius, its inner and outer radius. More... | |
| class | TGeoVolume |
| TGeoVolume, TGeoVolumeMulti, TGeoVolumeAssembly are the volume classes. More... | |
| class | TGeoXtru |
| A TGeoXtru shape is represented by the extrusion of an arbitrary polygon with fixed outline between several Z sections. More... | |