fitConvolution.py File Reference

Namespaces
namespace	fitConvolution

Detailed Description

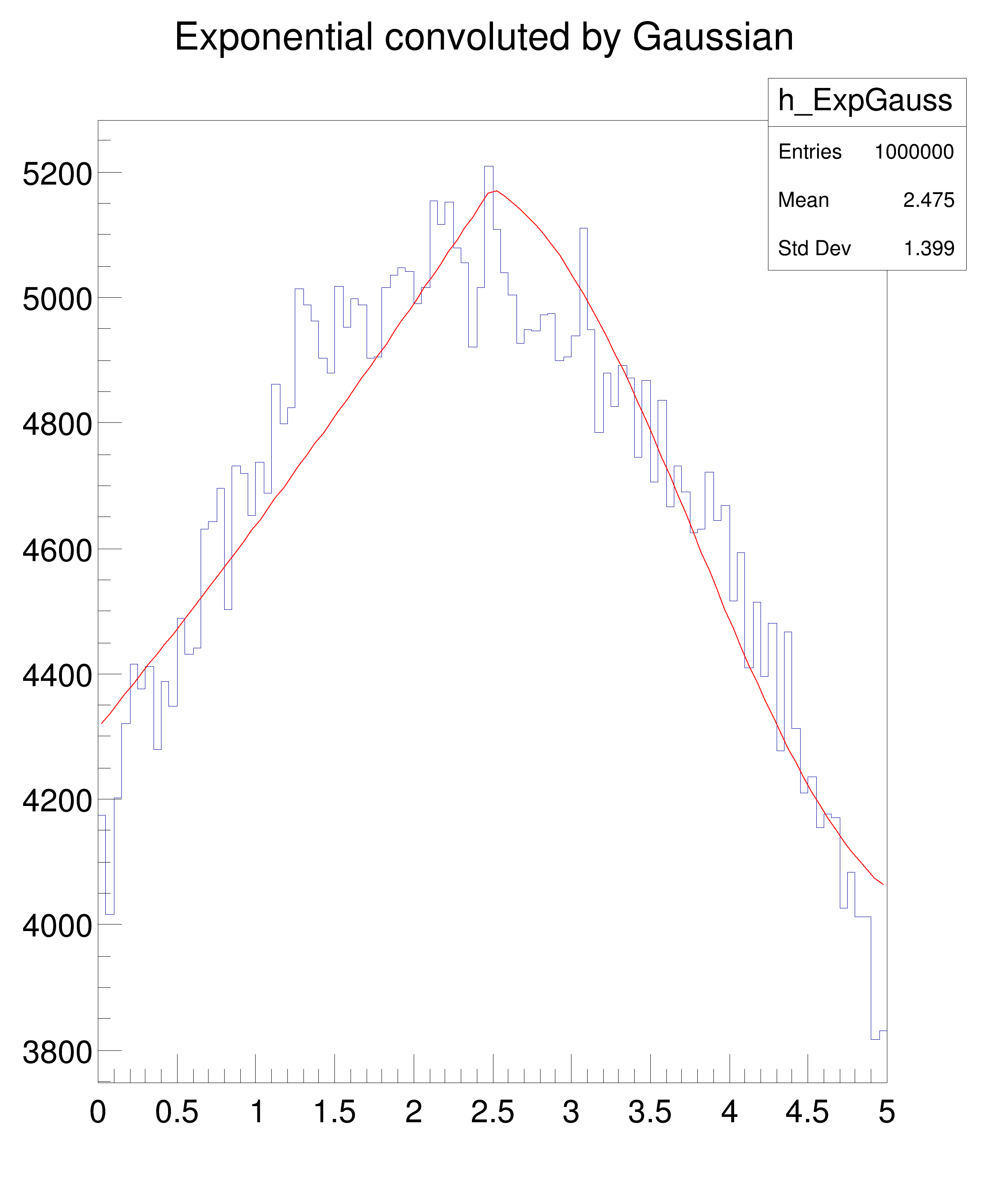
Tutorial for convolution of two functions

****************************************
Minimizer is Minuit2 / Migrad
Chi2                      =       298.12
NDf                       =           96
Edm                       =  1.67196e-06
NCalls                    =          448
p0                        =      7.32861   +/-   0.0370492   
p1                        =    0.0733018   +/-   0.00243973  
p2                        =     -2.26418   +/-   0.0491372   
p3                        =      1.12808   +/-   0.0628185   

 
import ROOT
 
# Construction of histogram to fit.
h_ExpGauss = ROOT.TH1F("h_ExpGauss", "Exponential convoluted by Gaussian", 100, 0.0, 5.0)
for i in range(1000000):
    # Gives a alpha of -0.3 in the exp.
    x = ROOT.gRandom.Exp(1.0 / 0.3)
    x += ROOT.gRandom.Gaus(0.0, 3.0)
    # Probability density function of the addition of two variables is the
    # convolution of two density functions.
    h_ExpGauss.Fill(x)
 
f_conv = ROOT.TF1Convolution("expo", "gaus", -1, 6, True)
f_conv.SetRange(-1.0, 6.0)
f_conv.SetNofPointsFFT(1000)
f = ROOT.TF1("f", f_conv, 0.0, 5.0, f_conv.GetNpar())
f.SetParameters(1.0, -0.3, 0.0, 1.0)
 
# Fit.
c1 = ROOT.TCanvas("c", "c", 800, 1000)
h_ExpGauss.Fit("f")
h_ExpGauss.Draw()
 
c1.SaveAs("fitConvolution.png")

Author

Jonas Rembser, Aurelie Flandi (C++ version)

Definition in file fitConvolution.py.