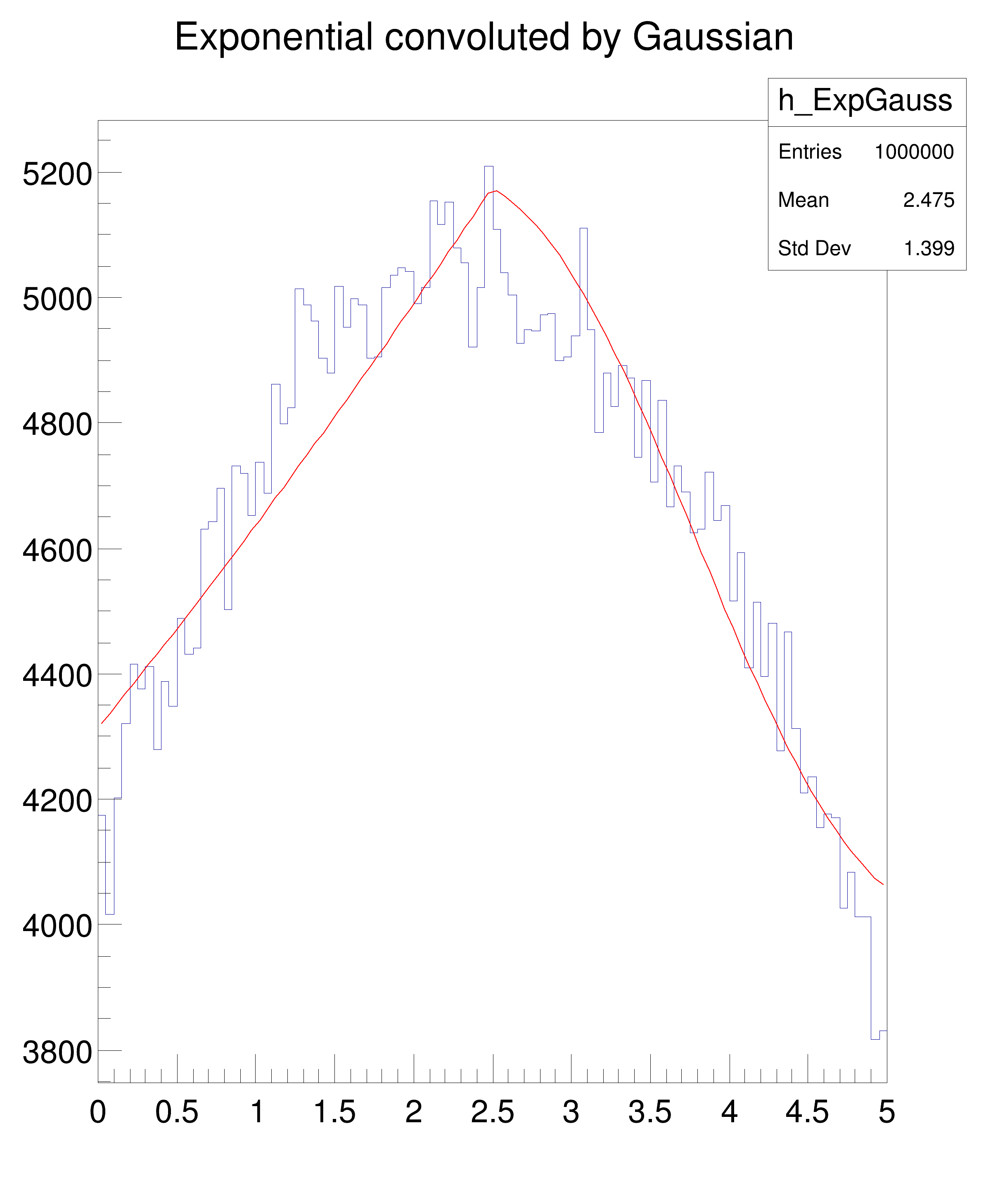
Tutorial for convolution of two functions
FCN=298.12 FROM MIGRAD STATUS=CONVERGED 457 CALLS 458 TOTAL
EDM=1.08093e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 7.32859e+00 3.70795e-02 1.23437e-05 -3.46193e-02
2 p1 7.33040e-02 2.44083e-03 3.62176e-06 -7.16223e-02
3 p2 -2.26420e+00 4.91803e-02 5.24021e-05 -1.27917e-02
4 p3 1.12811e+00 6.28810e-02 1.94847e-05 -2.72591e-02
import ROOT
h_ExpGauss = ROOT.TH1F("h_ExpGauss", "Exponential convoluted by Gaussian", 100, 0.0, 5.0)
for i in range(1000000):
x = ROOT.gRandom.Exp(1.0 / 0.3)
x += ROOT.gRandom.Gaus(0.0, 3.0)
h_ExpGauss.Fill(x)
f_conv = ROOT.TF1Convolution("expo", "gaus", -1, 6, True)
f_conv.SetRange(-1.0, 6.0)
f_conv.SetNofPointsFFT(1000)
f = ROOT.TF1("f", f_conv, 0.0, 5.0, f_conv.GetNpar())
f.SetParameters(1.0, -0.3, 0.0, 1.0)
c1 = ROOT.TCanvas("c", "c", 800, 1000)
h_ExpGauss.Fit("f")
h_ExpGauss.Draw()
c1.SaveAs("fitConvolution.png")
- Author
- Jonas Rembser, Aurelie Flandi (C++ version)
Definition in file fitConvolution.py.