StandardFeldmanCousinsDemo.C File Reference

Detailed Description

Standard demo of the Feldman-Cousins calculator StandardFeldmanCousinsDemo

This is a standard demo that can be used with any ROOT file prepared in the standard way. You specify:

• name for input ROOT file
• name of workspace inside ROOT file that holds model and data
• name of ModelConfig that specifies details for calculator tools
• name of dataset

With default parameters the macro will attempt to run the standard hist2workspace example and read the ROOT file that it produces.

The actual heart of the demo is only about 10 lines long.

The FeldmanCousins tools is a classical frequentist calculation based on the Neyman Construction. The test statistic can be generalized for nuisance parameters by using the profile likelihood ratio. But unlike the ProfileLikelihoodCalculator, this tool explicitly builds the sampling distribution of the test statistic via toy Monte Carlo.

 
 
=== Using the following for ModelConfig ===
Observables:             RooArgSet:: = (obs_x_channel1,channelCat)
Parameters of Interest:  RooArgSet:: = (SigXsecOverSM)
Nuisance Parameters:     RooArgSet:: = (alpha_syst2,alpha_syst3,gamma_stat_channel1_bin_0,gamma_stat_channel1_bin_1)
Global Observables:      RooArgSet:: = (nominalLumi,nom_alpha_syst1,nom_alpha_syst2,nom_alpha_syst3,nom_gamma_stat_channel1_bin_0,nom_gamma_stat_channel1_bin_1)
PDF:                     RooSimultaneous::simPdf[ indexCat=channelCat channel1=model_channel1 ] = 0.190787
 
FeldmanCousins: ntoys per point: adaptive
FeldmanCousins: nEvents per toy will fluctuate about  expectation
FeldmanCousins: Model has nuisance parameters, will do profile construction
FeldmanCousins: # points to test = 10
lookup index = 0
NeymanConstruction: Prog: 1/10 total MC = 78 this test stat = 1.323
 SigXsecOverSM=0.15 alpha_syst2=0.602165 alpha_syst3=0.227784 gamma_stat_channel1_bin_0=1.03121 gamma_stat_channel1_bin_1=1.04626 [-1e+30, 3.00321]  in interval = 1
 
NeymanConstruction: Prog: 2/10 total MC = 78 this test stat = 0.62223
 SigXsecOverSM=0.45 alpha_syst2=0.398328 alpha_syst3=0.161336 gamma_stat_channel1_bin_0=1.02058 gamma_stat_channel1_bin_1=1.03265 [-1e+30, 2.02972]  in interval = 1
 
NeymanConstruction: Prog: 3/10 total MC = 78 this test stat = 0.185526
 SigXsecOverSM=0.75 alpha_syst2=0.208868 alpha_syst3=0.0960168 gamma_stat_channel1_bin_0=1.01066 gamma_stat_channel1_bin_1=1.01935 [-1e+30, 1.36211]  in interval = 1
 
NeymanConstruction: Prog: 4/10 total MC = 78 this test stat = 0.00588515
 SigXsecOverSM=1.05 alpha_syst2=0.0298378 alpha_syst3=0.0322641 gamma_stat_channel1_bin_0=1.00149 gamma_stat_channel1_bin_1=1.00622 [-1e+30, 1.11847]  in interval = 1
 
NeymanConstruction: Prog: 5/10 total MC = 78 this test stat = 0.0747855
 SigXsecOverSM=1.35 alpha_syst2=-0.143781 alpha_syst3=-0.0340579 gamma_stat_channel1_bin_0=0.992877 gamma_stat_channel1_bin_1=0.994111 [-1e+30, 2.18053]  in interval = 1
 
NeymanConstruction: Prog: 6/10 total MC = 78 this test stat = 0.38368
 SigXsecOverSM=1.65 alpha_syst2=-0.306378 alpha_syst3=-0.0939576 gamma_stat_channel1_bin_0=0.985116 gamma_stat_channel1_bin_1=0.981396 [-1e+30, 1.59882]  in interval = 1
 
NeymanConstruction: Prog: 7/10 total MC = 78 this test stat = 0.924288
 SigXsecOverSM=1.95 alpha_syst2=-0.459983 alpha_syst3=-0.155793 gamma_stat_channel1_bin_0=0.977825 gamma_stat_channel1_bin_1=0.96944 [-1e+30, 2.13401]  in interval = 1
 
NeymanConstruction: Prog: 8/10 total MC = 78 this test stat = 1.68871
 SigXsecOverSM=2.25 alpha_syst2=-0.601899 alpha_syst3=-0.216148 gamma_stat_channel1_bin_0=0.97107 gamma_stat_channel1_bin_1=0.957726 [-1e+30, 2.12322]  in interval = 1
 
NeymanConstruction: Prog: 9/10 total MC = 234 this test stat = 2.66932
 SigXsecOverSM=2.55 alpha_syst2=-0.732216 alpha_syst3=-0.275843 gamma_stat_channel1_bin_0=0.964735 gamma_stat_channel1_bin_1=0.946434 [-1e+30, 2.20603]  in interval = 0
 
NeymanConstruction: Prog: 10/10 total MC = 234 this test stat = 3.85852
 SigXsecOverSM=2.85 alpha_syst2=-0.851841 alpha_syst3=-0.333911 gamma_stat_channel1_bin_0=0.958834 gamma_stat_channel1_bin_1=0.935422 [-1e+30, 2.28476]  in interval = 0
 
[#1] INFO:Eval -- 8 points in interval
 
95% interval on SigXsecOverSM is : [0.15, 2.25] 

 
#include "TFile.h"
#include "TROOT.h"
#include "TH1F.h"
#include "TSystem.h"
 
#include "RooWorkspace.h"
#include "RooAbsData.h"
 
#include "RooStats/ModelConfig.h"
#include "RooStats/FeldmanCousins.h"
#include "RooStats/ToyMCSampler.h"
#include "RooStats/PointSetInterval.h"
#include "RooStats/ConfidenceBelt.h"
 
using namespace RooFit;
using namespace RooStats;
 
void StandardFeldmanCousinsDemo(const char *infile = "", const char *workspaceName = "combined",
                                const char *modelConfigName = "ModelConfig", const char *dataName = "obsData")
{
 
   // -------------------------------------------------------
   // First part is just to access a user-defined file
   // or create the standard example file if it doesn't exist
   const char *filename = "";
   if (!strcmp(infile, "")) {
      filename = "results/example_combined_GaussExample_model.root";
      bool fileExist = !gSystem->AccessPathName(filename); // note opposite return code
      // if file does not exists generate with histfactory
      if (!fileExist) {
#ifdef _WIN32
         cout << "HistFactory file cannot be generated on Windows - exit" << endl;
         return;
#endif
         // Normally this would be run on the command line
         cout << "will run standard hist2workspace example" << endl;
         gROOT->ProcessLine(".! prepareHistFactory .");
         gROOT->ProcessLine(".! hist2workspace config/example.xml");
         cout << "\n\n---------------------" << endl;
         cout << "Done creating example input" << endl;
         cout << "---------------------\n\n" << endl;
      }
 
   } else
      filename = infile;
 
   // Try to open the file
   TFile *file = TFile::Open(filename);
 
   // if input file was specified byt not found, quit
   if (!file) {
      cout << "StandardRooStatsDemoMacro: Input file " << filename << " is not found" << endl;
      return;
   }
 
   // -------------------------------------------------------
   // Tutorial starts here
   // -------------------------------------------------------
 
   // get the workspace out of the file
   RooWorkspace *w = (RooWorkspace *)file->Get(workspaceName);
   if (!w) {
      cout << "workspace not found" << endl;
      return;
   }
 
   // get the modelConfig out of the file
   ModelConfig *mc = (ModelConfig *)w->obj(modelConfigName);
 
   // get the modelConfig out of the file
   RooAbsData *data = w->data(dataName);
 
   // make sure ingredients are found
   if (!data || !mc) {
      w->Print();
      cout << "data or ModelConfig was not found" << endl;
      return;
   }
 
   // -------------------------------------------------------
   // create and use the FeldmanCousins tool
   // to find and plot the 95% confidence interval
   // on the parameter of interest as specified
   // in the model config
   FeldmanCousins fc(*data, *mc);
   fc.SetConfidenceLevel(0.95); // 95% interval
   // fc.AdditionalNToysFactor(0.1); // to speed up the result
   fc.UseAdaptiveSampling(true); // speed it up a bit
   fc.SetNBins(10);              // set how many points per parameter of interest to scan
   fc.CreateConfBelt(true);      // save the information in the belt for plotting
 
   // Since this tool needs to throw toy MC the PDF needs to be
   // extended or the tool needs to know how many entries in a dataset
   // per pseudo experiment.
   // In the 'number counting form' where the entries in the dataset
   // are counts, and not values of discriminating variables, the
   // datasets typically only have one entry and the PDF is not
   // extended.
   if (!mc->GetPdf()->canBeExtended()) {
      if (data->numEntries() == 1)
         fc.FluctuateNumDataEntries(false);
      else
         cout << "Not sure what to do about this model" << endl;
   }
 
   // We can use PROOF to speed things along in parallel
   //  ProofConfig pc(*w, 1, "workers=4", kFALSE);
   //  ToyMCSampler*  toymcsampler = (ToyMCSampler*) fc.GetTestStatSampler();
   //  toymcsampler->SetProofConfig(&pc); // enable proof
 
   // Now get the interval
   PointSetInterval *interval = fc.GetInterval();
   ConfidenceBelt *belt = fc.GetConfidenceBelt();
 
   // print out the interval on the first Parameter of Interest
   RooRealVar *firstPOI = (RooRealVar *)mc->GetParametersOfInterest()->first();
   cout << "\n95% interval on " << firstPOI->GetName() << " is : [" << interval->LowerLimit(*firstPOI) << ", "
        << interval->UpperLimit(*firstPOI) << "] " << endl;
 
   // ---------------------------------------------
   // No nice plots yet, so plot the belt by hand
 
   // Ask the calculator which points were scanned
   RooDataSet *parameterScan = (RooDataSet *)fc.GetPointsToScan();
   RooArgSet *tmpPoint;
 
   // make a histogram of parameter vs. threshold
   TH1F *histOfThresholds =
      new TH1F("histOfThresholds", "", parameterScan->numEntries(), firstPOI->getMin(), firstPOI->getMax());
 
   // loop through the points that were tested and ask confidence belt
   // what the upper/lower thresholds were.
   // For FeldmanCousins, the lower cut off is always 0
   for (Int_t i = 0; i < parameterScan->numEntries(); ++i) {
      tmpPoint = (RooArgSet *)parameterScan->get(i)->clone("temp");
      double arMax = belt->GetAcceptanceRegionMax(*tmpPoint);
      double arMin = belt->GetAcceptanceRegionMax(*tmpPoint);
      double poiVal = tmpPoint->getRealValue(firstPOI->GetName());
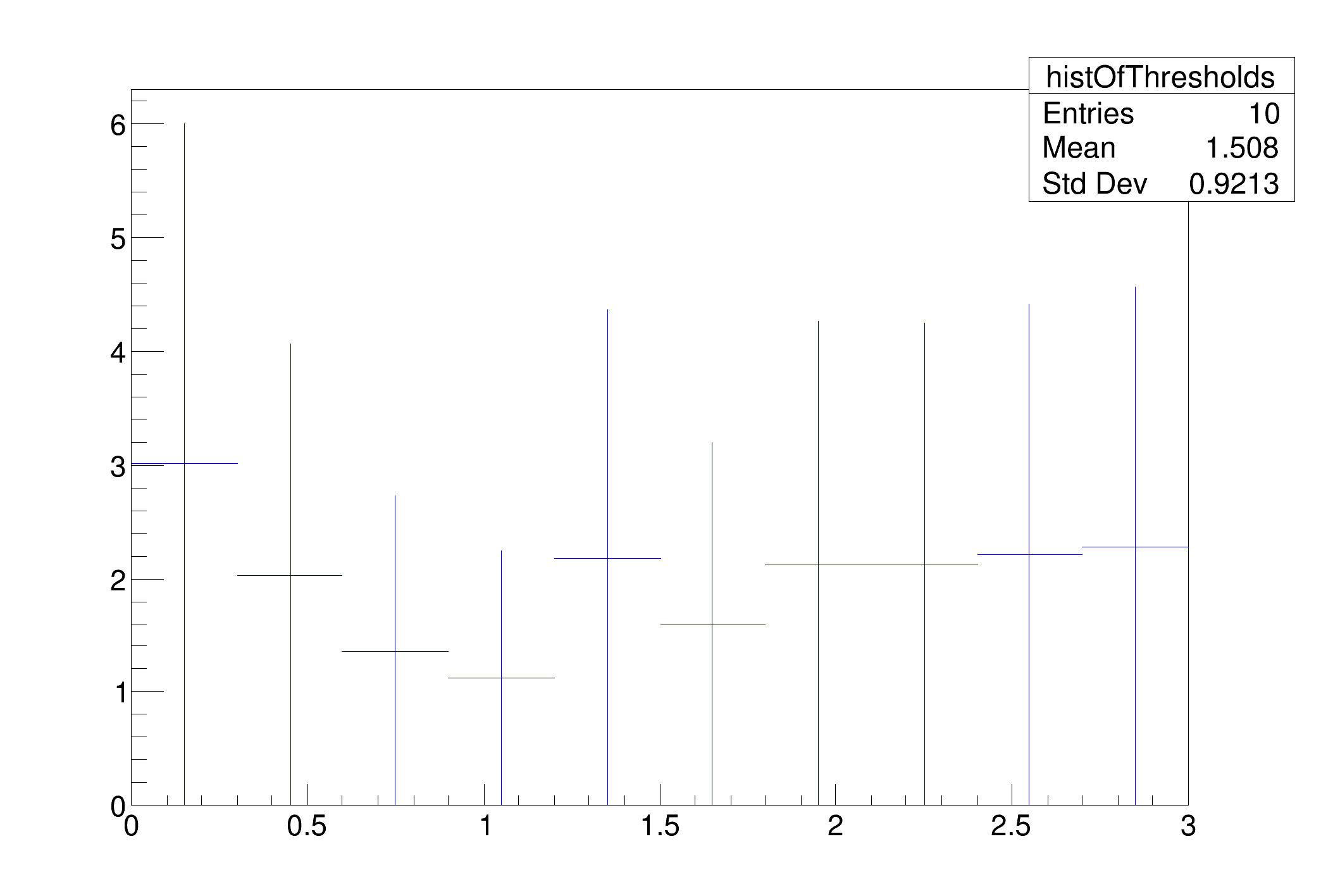
      histOfThresholds->Fill(poiVal, arMax);
   }
   histOfThresholds->SetMinimum(0);
   histOfThresholds->Draw();
}

Author

Kyle Cranmer

Definition in file StandardFeldmanCousinsDemo.C.