Class to handle efficiency histograms.
This class handles the calculation of efficiencies and their uncertainties. It provides several statistical methods for calculating frequentist and Bayesian confidence intervals as well as a function for combining several efficiencies.
Efficiencies have a lot of applications and meanings but in principle, they can be described by the fraction of good/passed events k out of sample containing N events. One is usually interested in the dependency of the efficiency on other (binned) variables. The number of passed and total events is therefore stored internally in two histograms (TEfficiency::fTotalHistogram and TEfficiency::fPassedHistogram). Then the efficiency, as well as its upper and lower error, can be calculated for each bin individually.
As the efficiency can be regarded as a parameter of a binomial distribution, the number of passed and total events must always be integer numbers. Therefore a filling with weights is not possible. However, you can assign a global weight to each TEfficiency object (TEfficiency::SetWeight). It is necessary to create one TEfficiency object for each weight if you investigate a process involving different weights. This procedure needs more effort but enables you to re-use the filled object in cases where you want to change one or more weights. This would not be possible if all events with different weights were filled in the same histogram.
If you start a new analysis, it is highly recommended to use the TEfficiency class from the beginning. You can then use one of the constructors for fixed or variable bin size and your desired dimension. These constructors append the created TEfficiency object to the current directory. So it will be written automatically to a file during the next TFile::Write command.
Example: create a two-dimensional TEfficiency object with
TEfficiency* pEff = new TEfficiency("eff","my efficiency;x;y;#epsilon",10,0,10,20,-5,5);
If you already have two histograms filled with the number of passed and total events, you will use the constructor TEfficiency(const TH1& passed,const TH1& total) to construct the TEfficiency object. The histograms "passed" and "total" have to fulfill the conditions mentioned in TEfficiency::CheckConsistency, otherwise the construction will fail. As the histograms already exist, the new TEfficiency is by default not attached to the current directory to avoid duplication of data. If you want to store the new object anyway, you can either write it directly by calling TObject::Write or attach it to a directory using TEfficiency::SetDirectory. This also applies to TEfficiency objects created by the copy constructor TEfficiency::TEfficiency(const TEfficiency& rEff).In case you already have two filled histograms and you only want to plot them as a graph, you should rather use TGraphAsymmErrors::TGraphAsymmErrors(const TH1* pass,const TH1* total,Option_t* opt) to create a graph object.
You can fill the TEfficiency object by calling the TEfficiency::Fill(Bool_t bPassed,Double_t x,Double_t y,Double_t z) method. The "bPassed" boolean flag indicates whether the current event is good (both histograms are filled) or not (only TEfficiency::fTotalHistogram is filled). The x, y and z variables determine the bin which is filled. For lower dimensions, the z- or even the y-value may be omitted.

You can also set the number of passed or total events for a bin directly by using the TEfficiency::SetPassedEvents or TEfficiency::SetTotalEvents method.
The calculation of the estimated efficiency depends on the chosen statistic option. Let k denotes the number of passed events and N the number of total events.
The expectation value of the number of passed events is given by the true efficiency times the total number of events. One can estimate the efficiency by replacing the expected number of passed events by the observed number of passed events.
\[ k = \epsilon \times N \Rightarrow \hat{\varepsilon} = \frac{k}{N} \]
In Bayesian statistics a likelihood-function (how probable is it to get the observed data assuming a true efficiency) and a prior probability (what is the probability that a certain true efficiency is actually realised) are used to determine a posterior probability by using Bayes theorem. At the moment, only beta distributions (have 2 free parameters) are supported as prior probabilities.
\begin{eqnarray*} P(\epsilon | k ; N) &=& \frac{1}{norm} \times P(k | \epsilon ; N) \times Prior(\epsilon) \\ P(k | \epsilon ; N) &=& Binomial(N,k) \times \epsilon^{k} \times (1 - \epsilon)^{N - k} ...\ binomial\ distribution \\ Prior(\epsilon) &=& \frac{1}{B(\alpha,\beta)} \times \epsilon ^{\alpha - 1} \times (1 - \epsilon)^{\beta - 1} \equiv Beta(\epsilon; \alpha,\beta) \\ \Rightarrow P(\epsilon | k ; N) &=& \frac{1}{norm'} \times \epsilon^{k + \alpha - 1} \times (1 - \epsilon)^{N - k + \beta - 1} \equiv Beta(\epsilon; k + \alpha, N - k + \beta) \end{eqnarray*}
By default the expectation value of this posterior distribution is used as an estimator for the efficiency:
\[ \hat{\varepsilon} = \frac{k + \alpha}{N + \alpha + \beta} \]
Optionally the mode can also be used as a value for the estimated efficiency. This can be done by calling SetBit(kPosteriorMode) or TEfficiency::SetPosteriorMode. In this case, the estimated efficiency is:
\[ \hat{\varepsilon} = \frac{k + \alpha -1}{N + \alpha + \beta - 2} \]
In the case of a uniform prior distribution, B(x,1,1), the posterior mode is k/n, equivalent to the frequentist estimate (the maximum likelihood value).
The statistic options also specify which confidence interval is used for calculating the uncertainties of the efficiency. The following properties define the error calculation:
In the following table, the implemented confidence intervals are listed with their corresponding statistic option. For more details on the calculation, please have a look at the mentioned functions.
| name | statistic option | function | kIsBayesian | parameters |
|---|---|---|---|---|
| Clopper-Pearson | kFCP | TEfficiency::ClopperPearson | false | total events, passed events, confidence level |
| normal approximation | kFNormal | TEfficiency::Normal | false | total events, passed events, confidence level |
| Wilson | kFWilson | TEfficiency::Wilson | false | total events, passed events, confidence level |
| Agresti-Coull | kFAC | TEfficiency::AgrestiCoull | false | total events, passed events. confidence level |
| Feldman-Cousins | kFFC | TEfficiency::FeldmanCousins | false | total events, passed events, confidence level |
| Mid-P Lancaster | kMidP | TEfficiency::MidPInterval | false | total events, passed events, confidence level |
| Jeffrey | kBJeffrey | TEfficiency::Bayesian | true | total events, passed events, confidence level, fBeta_alpha = 0.5, fBeta_beta = 0.5 |
| Uniform prior | kBUniform | TEfficiency::Bayesian | true | total events, passed events, confidence level, fBeta_alpha = 1, fBeta_beta = 1 |
| custom prior | kBBayesian | TEfficiency::Bayesian | true | total events, passed events, confidence level, fBeta_alpha, fBeta_beta |
The following example demonstrates the effect of different statistic options and confidence levels.

The prior probability of the efficiency in Bayesian statistics can be given in terms of a beta distribution. The beta distribution has two positive shape parameters. The resulting priors for different combinations of these shape parameters are shown in the plot below.

The following pictures illustrate the actual coverage probability for the different values of the true efficiency and the total number of events when a confidence level of 95% is desired.

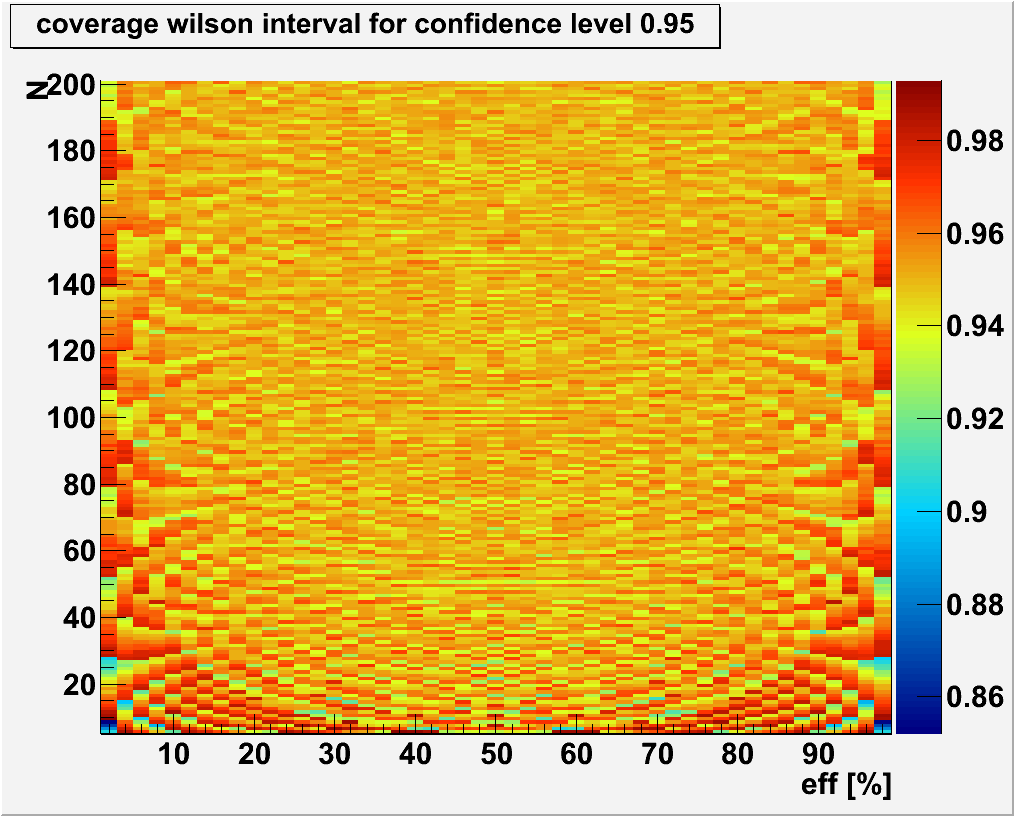



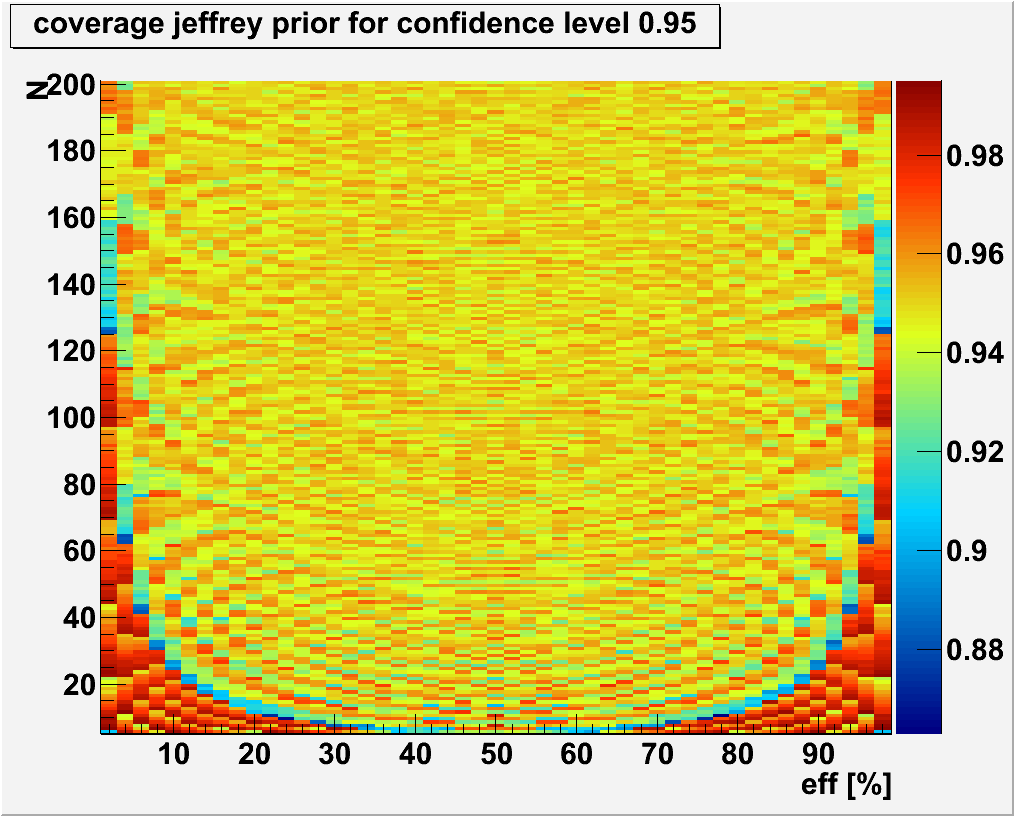
The average (over all possible true efficiencies) coverage probability for different number of total events is shown in the next picture.

In many applications, the efficiency should be calculated for an inhomogeneous sample in the sense that it contains events with different weights. In order to be able to determine the correct overall efficiency, it is necessary to use for each subsample (= all events with the same weight) a different TEfficiency object. After finishing your analysis you can then construct the overall efficiency with its uncertainty.
This procedure has the advantage that you can change the weight of one subsample easily without rerunning the whole analysis. On the other hand, more effort is needed to handle several TEfficiency objects instead of one histogram. In the case of many different or even continuously distributed weights, this approach becomes cumbersome. One possibility to overcome this problem is the usage of binned weights.
In particle physics weights arises from the fact that you want to normalise your results to a certain reference value. A very common formula for calculating weights is
\begin{eqnarray*} w &=& \frac{\sigma L}{N_{gen} \epsilon_{trig}} \\ &-& \sigma ...\ cross\ section \\ &-& L ...\ luminosity \\ &-& N_{gen}\ ... number\ of\ generated\ events \\ &-& \epsilon_{trig}\ ...\ (known)\ trigger\ efficiency \\ \end{eqnarray*}
The reason for different weights can therefore be:
Depending on the actual meaning of different weights in your case, you should either merge or combine them to get the overall efficiency.
If the weights are artificial and do not represent real alternative hypotheses, you should merge the different TEfficiency objects. That means especially for the Bayesian case that the prior probability should be the same for all merged TEfficiency objects. The merging can be done by invoking one of the following operations:
The result of the merging is stored in the TEfficiency object which is marked bold above. The contents of the internal histograms of both TEfficiency objects are added and a new weight is assigned. The statistic options are not changed.
\[ \frac{1}{w_{new}} = \frac{1}{w_{1}} + \frac{1}{w_{2}} \]
If you use two samples with different numbers of generated events for the same process and you want to normalise both to the same integrated luminosity and trigger efficiency, the different weights then arise just from the fact that you have different numbers of events. The TEfficiency objects should be merged because the samples do not represent true alternatives. You expect the same result as if you would have a big sample with all events in it.
\[ w_{1} = \frac{\sigma L}{\epsilon N_{1}}, w_{2} = \frac{\sigma L}{\epsilon N_{2}} \Rightarrow w_{new} = \frac{\sigma L}{\epsilon (N_{1} + N_{2})} = \frac{1}{\frac{1}{w_{1}} + \frac{1}{w_{2}}} \]
You should combine TEfficiency objects whenever the weights represent alternatives processes for the efficiency. As the combination of two TEfficiency objects is not always consistent with the representation by two internal histograms, the result is not stored in a TEfficiency object but a TGraphAsymmErrors is returned which shows the estimated combined efficiency and its uncertainty for each bin. At the moment the combination method TEfficiency::Combine only supports a combination of 1-dimensional efficiencies in a Bayesian approach.
For calculating the combined efficiency and its uncertainty for each bin only Bayesian statistics is used. No frequentists methods are presently supported for computing the combined efficiency and its confidence interval. In the case of the Bayesian statistics, a combined posterior is constructed taking into account the weight of each TEfficiency object. The same prior is used for all the TEfficiency objects.
\begin{eqnarray*} P_{comb}(\epsilon | {w_{i}}, {k_{i}} , {N_{i}}) = \frac{1}{norm} \prod_{i}{L(k_{i} | N_{i}, \epsilon)}^{w_{i}} \Pi( \epsilon )\\ L(k_{i} | N_{i}, \epsilon)\ is\ the\ likelihood\ function\ for\ the\ sample\ i\ (a\ Binomial\ distribution)\\ \Pi( \epsilon)\ is\ the\ prior,\ a\ beta\ distribution\ B(\epsilon, \alpha, \beta).\\ The\ resulting\ combined\ posterior\ is \\ P_{comb}(\epsilon |{w_{i}}; {k_{i}}; {N_{i}}) = B(\epsilon, \sum_{i}{ w_{i} k_{i}} + \alpha, \sum_{i}{ w_{i}(n_{i}-k_{i})}+\beta) \\ \hat{\varepsilon} = \int_{0}^{1} \epsilon \times P_{comb}(\epsilon | {k_{i}} , {N_{i}}) d\epsilon \\ confidence\ level = 1 - \alpha \\ \frac{\alpha}{2} = \int_{0}^{\epsilon_{low}} P_{comb}(\epsilon | {k_{i}} , {N_{i}}) d\epsilon ...\ defines\ lower\ boundary \\ 1- \frac{\alpha}{2} = \int_{0}^{\epsilon_{up}} P_{comb}(\epsilon | {k_{i}} , {N_{i}}) d\epsilon ...\ defines\ upper\ boundary \end{eqnarray*}
If you use cuts to select electrons which can originate from two different processes, you can determine the selection efficiency for each process. The overall selection efficiency is then the combined efficiency. The weights to be used in the combination should be the probability that an electron comes from the corresponding process.
\[ p_{1} = \frac{\sigma_{1}}{\sigma_{1} + \sigma_{2}} = \frac{N_{1}w_{1}}{N_{1}w_{1} + N_{2}w_{2}}\\ p_{2} = \frac{\sigma_{2}}{\sigma_{1} + \sigma_{2}} = \frac{N_{2}w_{2}}{N_{1}w_{1} + N_{2}w_{2}} \]
The methods TEfficiency::GetPassedHistogram and TEfficiency::GetTotalHistogram return a constant pointer to the internal histograms. They can be used to obtain information about the internal histograms (e.g., the binning, number of passed / total events in a bin, mean values...). One can obtain a clone of the internal histograms by calling TEfficiency::GetCopyPassedHisto or TEfficiency::GetCopyTotalHisto. The returned histograms are completely independent from the current TEfficiency object. By default, they are not attached to a directory to avoid the duplication of data and the user is responsible for deleting them.
It is also possible to set the internal total or passed histogram by using the methods TEfficiency::SetPassedHistogram or TEfficiency::SetTotalHistogram.
In order to ensure the validity of the TEfficiency object, the consistency of the new histogram and the stored histogram is checked. It might be impossible sometimes to change the histograms in a consistent way. Therefore one can force the replacement by passing the "f" option. Then the user has to ensure that the other internal histogram is replaced as well and that the TEfficiency object is in a valid state.
The efficiency can be fitted using the TEfficiency::Fit function which internally uses the TBinomialEfficiencyFitter::Fit method. As this method is using a maximum-likelihood-fit, it is necessary to initialise the given fit function with reasonable start values. The resulting fit function is attached to the list of associated functions and will be drawn automatically during the next TEfficiency::Draw command. The list of associated function can be modified by using the pointer returned by TEfficiency::GetListOfFunctions.

A TEfficiency object can be drawn by calling the usual TEfficiency::Draw method. At the moment drawing is only supported for 1- and 2-dimensional TEfficiency objects. In the 1-dimensional case, you can use the same options as for the TGraphAsymmErrors::Draw method. For 2-dimensional TEfficiency objects, you can pass the same options as for a TH2::Draw object.
Definition at line 27 of file TEfficiency.h.
Public Types | |
| enum | EStatOption { kFCP = 0 , kFNormal , kFWilson , kFAC , kFFC , kBJeffrey , kBUniform , kBBayesian , kMidP } |
| Enumeration type for different statistic options for calculating confidence intervals kF* ... frequentist methods; kB* ... bayesian methods. More... | |
 Public Types inherited from TObject Public Types inherited from TObject | |
| enum | { kIsOnHeap = 0x01000000 , kNotDeleted = 0x02000000 , kZombie = 0x04000000 , kInconsistent = 0x08000000 , kBitMask = 0x00ffffff } |
| enum | { kSingleKey = BIT(0) , kOverwrite = BIT(1) , kWriteDelete = BIT(2) } |
| enum | EDeprecatedStatusBits { kObjInCanvas = BIT(3) } |
| enum | EStatusBits { kCanDelete = BIT(0) , kMustCleanup = BIT(3) , kIsReferenced = BIT(4) , kHasUUID = BIT(5) , kCannotPick = BIT(6) , kNoContextMenu = BIT(8) , kInvalidObject = BIT(13) } |
Public Member Functions | |
| TEfficiency () | |
| Default constructor. | |
| TEfficiency (const char *name, const char *title, Int_t nbins, const Double_t *xbins) | |
| Create 1-dimensional TEfficiency object with variable bin size. | |
| TEfficiency (const char *name, const char *title, Int_t nbins, Double_t xlow, Double_t xup) | |
| Create 1-dimensional TEfficiency object with fixed bins size. | |
| TEfficiency (const char *name, const char *title, Int_t nbinsx, const Double_t *xbins, Int_t nbinsy, const Double_t *ybins) | |
| Create 2-dimensional TEfficiency object with variable bin size. | |
| TEfficiency (const char *name, const char *title, Int_t nbinsx, const Double_t *xbins, Int_t nbinsy, const Double_t *ybins, Int_t nbinsz, const Double_t *zbins) | |
| Create 3-dimensional TEfficiency object with variable bin size. | |
| TEfficiency (const char *name, const char *title, Int_t nbinsx, Double_t xlow, Double_t xup, Int_t nbinsy, Double_t ylow, Double_t yup) | |
| Create 2-dimensional TEfficiency object with fixed bin size. | |
| TEfficiency (const char *name, const char *title, Int_t nbinsx, Double_t xlow, Double_t xup, Int_t nbinsy, Double_t ylow, Double_t yup, Int_t nbinsz, Double_t zlow, Double_t zup) | |
| Create 3-dimensional TEfficiency object with fixed bin size. | |
| TEfficiency (const TEfficiency &heff) | |
| Copy constructor. | |
| TEfficiency (const TH1 &passed, const TH1 &total) | |
| Constructor using two existing histograms as input. | |
| ~TEfficiency () | |
| default destructor | |
| void | Add (const TEfficiency &rEff) |
| void | Browse (TBrowser *) |
| Browse object. May be overridden for another default action. | |
| TGraphAsymmErrors * | CreateGraph (Option_t *opt="") const |
| Create the graph used be painted (for dim=1 TEfficiency) The return object is managed by the caller. | |
| TH2 * | CreateHistogram (Option_t *opt="") const |
| Create the histogram used to be painted (for dim=2 TEfficiency) The return object is managed by the caller. | |
| virtual Int_t | DistancetoPrimitive (Int_t px, Int_t py) |
| Compute distance from point px,py to a graph. | |
| void | Draw (Option_t *opt="") |
| Draws the current TEfficiency object. | |
| virtual void | ExecuteEvent (Int_t event, Int_t px, Int_t py) |
| Execute action corresponding to one event. | |
| void | Fill (Bool_t bPassed, Double_t x, Double_t y=0, Double_t z=0) |
| This function is used for filling the two histograms. | |
| void | FillWeighted (Bool_t bPassed, Double_t weight, Double_t x, Double_t y=0, Double_t z=0) |
| This function is used for filling the two histograms with a weight. | |
| Int_t | FindFixBin (Double_t x, Double_t y=0, Double_t z=0) const |
| Returns the global bin number containing the given values. | |
| TFitResultPtr | Fit (TF1 *f1, Option_t *opt="") |
| Fits the efficiency using the TBinomialEfficiencyFitter class. | |
| Double_t | GetBetaAlpha (Int_t bin=-1) const |
| Double_t | GetBetaBeta (Int_t bin=-1) const |
| Double_t | GetConfidenceLevel () const |
| TH1 * | GetCopyPassedHisto () const |
| Returns a cloned version of fPassedHistogram. | |
| TH1 * | GetCopyTotalHisto () const |
| Returns a cloned version of fTotalHistogram. | |
| Int_t | GetDimension () const |
| returns the dimension of the current TEfficiency object | |
| TDirectory * | GetDirectory () const |
| Double_t | GetEfficiency (Int_t bin) const |
| Returns the efficiency in the given global bin. | |
| Double_t | GetEfficiencyErrorLow (Int_t bin) const |
| Returns the lower error on the efficiency in the given global bin. | |
| Double_t | GetEfficiencyErrorUp (Int_t bin) const |
| Returns the upper error on the efficiency in the given global bin. | |
| Int_t | GetGlobalBin (Int_t binx, Int_t biny=0, Int_t binz=0) const |
| Returns the global bin number which can be used as argument for the following functions: | |
| TList * | GetListOfFunctions () |
| TGraphAsymmErrors * | GetPaintedGraph () const |
| TH2 * | GetPaintedHistogram () const |
| const TH1 * | GetPassedHistogram () const |
| EStatOption | GetStatisticOption () const |
| const TH1 * | GetTotalHistogram () const |
| Double_t | GetWeight () const |
| Long64_t | Merge (TCollection *list) |
| Merges the TEfficiency objects in the given list to the given TEfficiency object using the operator+=(TEfficiency&) | |
| TEfficiency & | operator+= (const TEfficiency &rhs) |
| Adds the histograms of another TEfficiency object to current histograms. | |
| TEfficiency & | operator= (const TEfficiency &rhs) |
| Assignment operator. | |
| void | Paint (Option_t *opt) |
| Paints this TEfficiency object. | |
| void | SavePrimitive (std::ostream &out, Option_t *opt="") |
| Have histograms fixed bins along each axis? | |
| void | SetBetaAlpha (Double_t alpha) |
| Sets the shape parameter α. | |
| void | SetBetaBeta (Double_t beta) |
| Sets the shape parameter β. | |
| void | SetBetaBinParameters (Int_t bin, Double_t alpha, Double_t beta) |
| Sets different shape parameter α and β for the prior distribution for each bin. | |
| Bool_t | SetBins (Int_t nx, const Double_t *xBins) |
| Set the bins for the underlined passed and total histograms If the class have been already filled the previous contents will be lost. | |
| Bool_t | SetBins (Int_t nx, const Double_t *xBins, Int_t ny, const Double_t *yBins) |
| Set the bins for the underlined passed and total histograms If the class have been already filled the previous contents will be lost. | |
| Bool_t | SetBins (Int_t nx, const Double_t *xBins, Int_t ny, const Double_t *yBins, Int_t nz, const Double_t *zBins) |
| Set the bins for the underlined passed and total histograms If the class have been already filled the previous contents will be lost. | |
| Bool_t | SetBins (Int_t nx, Double_t xmin, Double_t xmax) |
| Set the bins for the underlined passed and total histograms If the class have been already filled the previous contents will be lost. | |
| Bool_t | SetBins (Int_t nx, Double_t xmin, Double_t xmax, Int_t ny, Double_t ymin, Double_t ymax) |
| Set the bins for the underlined passed and total histograms If the class have been already filled the previous contents will be lost. | |
| Bool_t | SetBins (Int_t nx, Double_t xmin, Double_t xmax, Int_t ny, Double_t ymin, Double_t ymax, Int_t nz, Double_t zmin, Double_t zmax) |
| Set the bins for the underlined passed and total histograms If the class have been already filled the previous contents will be lost. | |
| void | SetCentralInterval (Bool_t on=true) |
| void | SetConfidenceLevel (Double_t level) |
| Sets the confidence level (0 < level < 1) The default value is 1-sigma :~ 0.683. | |
| void | SetDirectory (TDirectory *dir) |
| Sets the directory holding this TEfficiency object. | |
| void | SetName (const char *name) |
| Sets the name. | |
| Bool_t | SetPassedEvents (Int_t bin, Int_t events) |
| Sets the number of passed events in the given global bin. | |
| Bool_t | SetPassedHistogram (const TH1 &rPassed, Option_t *opt) |
| Sets the histogram containing the passed events. | |
| void | SetPosteriorAverage (Bool_t on=true) |
| void | SetPosteriorMode (Bool_t on=true) |
| void | SetShortestInterval (Bool_t on=true) |
| void | SetStatisticOption (EStatOption option) |
| Sets the statistic option which affects the calculation of the confidence interval. | |
| void | SetTitle (const char *title) |
| Sets the title. | |
| Bool_t | SetTotalEvents (Int_t bin, Int_t events) |
| Sets the number of total events in the given global bin. | |
| Bool_t | SetTotalHistogram (const TH1 &rTotal, Option_t *opt) |
| Sets the histogram containing all events. | |
| void | SetUseWeightedEvents (Bool_t on=kTRUE) |
| void | SetWeight (Double_t weight) |
| Sets the global weight for this TEfficiency object. | |
| Bool_t | UsesBayesianStat () const |
| Bool_t | UsesCentralInterval () const |
| Bool_t | UsesPosteriorAverage () const |
| Bool_t | UsesPosteriorMode () const |
| Bool_t | UsesShortestInterval () const |
| Bool_t | UsesWeights () const |
 Public Member Functions inherited from TNamed Public Member Functions inherited from TNamed | |
| TNamed () | |
| TNamed (const char *name, const char *title) | |
| TNamed (const TNamed &named) | |
| TNamed copy ctor. | |
| TNamed (const TString &name, const TString &title) | |
| virtual | ~TNamed () |
| TNamed destructor. | |
| virtual void | Clear (Option_t *option="") |
| Set name and title to empty strings (""). | |
| virtual TObject * | Clone (const char *newname="") const |
| Make a clone of an object using the Streamer facility. | |
| virtual Int_t | Compare (const TObject *obj) const |
| Compare two TNamed objects. | |
| virtual void | Copy (TObject &named) const |
| Copy this to obj. | |
| virtual void | FillBuffer (char *&buffer) |
| Encode TNamed into output buffer. | |
| virtual const char * | GetName () const |
| Returns name of object. | |
| virtual const char * | GetTitle () const |
| Returns title of object. | |
| virtual ULong_t | Hash () const |
| Return hash value for this object. | |
| virtual Bool_t | IsSortable () const |
| virtual void | ls (Option_t *option="") const |
| List TNamed name and title. | |
| TNamed & | operator= (const TNamed &rhs) |
| TNamed assignment operator. | |
| virtual void | Print (Option_t *option="") const |
| Print TNamed name and title. | |
| virtual void | SetNameTitle (const char *name, const char *title) |
| Set all the TNamed parameters (name and title). | |
| virtual Int_t | Sizeof () const |
| Return size of the TNamed part of the TObject. | |
 Public Member Functions inherited from TObject Public Member Functions inherited from TObject | |
| TObject () | |
| TObject constructor. | |
| TObject (const TObject &object) | |
| TObject copy ctor. | |
| virtual | ~TObject () |
| TObject destructor. | |
| void | AbstractMethod (const char *method) const |
| Use this method to implement an "abstract" method that you don't want to leave purely abstract. | |
| virtual void | AppendPad (Option_t *option="") |
| Append graphics object to current pad. | |
| ULong_t | CheckedHash () |
| Check and record whether this class has a consistent Hash/RecursiveRemove setup (*) and then return the regular Hash value for this object. | |
| virtual const char * | ClassName () const |
| Returns name of class to which the object belongs. | |
| virtual void | Delete (Option_t *option="") |
| Delete this object. | |
| virtual void | DrawClass () const |
| Draw class inheritance tree of the class to which this object belongs. | |
| virtual TObject * | DrawClone (Option_t *option="") const |
Draw a clone of this object in the current selected pad for instance with: gROOT->SetSelectedPad(gPad). | |
| virtual void | Dump () const |
| Dump contents of object on stdout. | |
| virtual void | Error (const char *method, const char *msgfmt,...) const |
| Issue error message. | |
| virtual void | Execute (const char *method, const char *params, Int_t *error=0) |
| Execute method on this object with the given parameter string, e.g. | |
| virtual void | Execute (TMethod *method, TObjArray *params, Int_t *error=0) |
| Execute method on this object with parameters stored in the TObjArray. | |
| virtual void | Fatal (const char *method, const char *msgfmt,...) const |
| Issue fatal error message. | |
| virtual TObject * | FindObject (const char *name) const |
| Must be redefined in derived classes. | |
| virtual TObject * | FindObject (const TObject *obj) const |
| Must be redefined in derived classes. | |
| virtual Option_t * | GetDrawOption () const |
| Get option used by the graphics system to draw this object. | |
| virtual const char * | GetIconName () const |
| Returns mime type name of object. | |
| virtual char * | GetObjectInfo (Int_t px, Int_t py) const |
| Returns string containing info about the object at position (px,py). | |
| virtual Option_t * | GetOption () const |
| virtual UInt_t | GetUniqueID () const |
| Return the unique object id. | |
| virtual Bool_t | HandleTimer (TTimer *timer) |
| Execute action in response of a timer timing out. | |
| Bool_t | HasInconsistentHash () const |
| Return true is the type of this object is known to have an inconsistent setup for Hash and RecursiveRemove (i.e. | |
| virtual void | Info (const char *method, const char *msgfmt,...) const |
| Issue info message. | |
| virtual Bool_t | InheritsFrom (const char *classname) const |
| Returns kTRUE if object inherits from class "classname". | |
| virtual Bool_t | InheritsFrom (const TClass *cl) const |
| Returns kTRUE if object inherits from TClass cl. | |
| virtual void | Inspect () const |
| Dump contents of this object in a graphics canvas. | |
| void | InvertBit (UInt_t f) |
| Bool_t | IsDestructed () const |
| IsDestructed. | |
| virtual Bool_t | IsEqual (const TObject *obj) const |
| Default equal comparison (objects are equal if they have the same address in memory). | |
| virtual Bool_t | IsFolder () const |
| Returns kTRUE in case object contains browsable objects (like containers or lists of other objects). | |
| R__ALWAYS_INLINE Bool_t | IsOnHeap () const |
| R__ALWAYS_INLINE Bool_t | IsZombie () const |
| void | MayNotUse (const char *method) const |
| Use this method to signal that a method (defined in a base class) may not be called in a derived class (in principle against good design since a child class should not provide less functionality than its parent, however, sometimes it is necessary). | |
| virtual Bool_t | Notify () |
| This method must be overridden to handle object notification. | |
| void | Obsolete (const char *method, const char *asOfVers, const char *removedFromVers) const |
| Use this method to declare a method obsolete. | |
| void | operator delete (void *ptr) |
| Operator delete. | |
| void | operator delete[] (void *ptr) |
| Operator delete []. | |
| void * | operator new (size_t sz) |
| void * | operator new (size_t sz, void *vp) |
| void * | operator new[] (size_t sz) |
| void * | operator new[] (size_t sz, void *vp) |
| TObject & | operator= (const TObject &rhs) |
| TObject assignment operator. | |
| virtual void | Pop () |
| Pop on object drawn in a pad to the top of the display list. | |
| virtual Int_t | Read (const char *name) |
| Read contents of object with specified name from the current directory. | |
| virtual void | RecursiveRemove (TObject *obj) |
| Recursively remove this object from a list. | |
| void | ResetBit (UInt_t f) |
| virtual void | SaveAs (const char *filename="", Option_t *option="") const |
| Save this object in the file specified by filename. | |
| void | SetBit (UInt_t f) |
| void | SetBit (UInt_t f, Bool_t set) |
| Set or unset the user status bits as specified in f. | |
| virtual void | SetDrawOption (Option_t *option="") |
| Set drawing option for object. | |
| virtual void | SetUniqueID (UInt_t uid) |
| Set the unique object id. | |
| virtual void | SysError (const char *method, const char *msgfmt,...) const |
| Issue system error message. | |
| R__ALWAYS_INLINE Bool_t | TestBit (UInt_t f) const |
| Int_t | TestBits (UInt_t f) const |
| virtual void | UseCurrentStyle () |
| Set current style settings in this object This function is called when either TCanvas::UseCurrentStyle or TROOT::ForceStyle have been invoked. | |
| virtual void | Warning (const char *method, const char *msgfmt,...) const |
| Issue warning message. | |
| virtual Int_t | Write (const char *name=0, Int_t option=0, Int_t bufsize=0) |
| Write this object to the current directory. | |
| virtual Int_t | Write (const char *name=0, Int_t option=0, Int_t bufsize=0) const |
| Write this object to the current directory. | |
 Public Member Functions inherited from TAttLine Public Member Functions inherited from TAttLine | |
| TAttLine () | |
| AttLine default constructor. | |
| TAttLine (Color_t lcolor, Style_t lstyle, Width_t lwidth) | |
| AttLine normal constructor. | |
| virtual | ~TAttLine () |
| AttLine destructor. | |
| void | Copy (TAttLine &attline) const |
| Copy this line attributes to a new TAttLine. | |
| Int_t | DistancetoLine (Int_t px, Int_t py, Double_t xp1, Double_t yp1, Double_t xp2, Double_t yp2) |
| Compute distance from point px,py to a line. | |
| virtual Color_t | GetLineColor () const |
| Return the line color. | |
| virtual Style_t | GetLineStyle () const |
| Return the line style. | |
| virtual Width_t | GetLineWidth () const |
| Return the line width. | |
| virtual void | Modify () |
| Change current line attributes if necessary. | |
| virtual void | ResetAttLine (Option_t *option="") |
| Reset this line attributes to default values. | |
| virtual void | SaveLineAttributes (std::ostream &out, const char *name, Int_t coldef=1, Int_t stydef=1, Int_t widdef=1) |
| Save line attributes as C++ statement(s) on output stream out. | |
| virtual void | SetLineAttributes () |
| Invoke the DialogCanvas Line attributes. | |
| virtual void | SetLineColor (Color_t lcolor) |
| Set the line color. | |
| virtual void | SetLineColorAlpha (Color_t lcolor, Float_t lalpha) |
| Set a transparent line color. | |
| virtual void | SetLineStyle (Style_t lstyle) |
| Set the line style. | |
| virtual void | SetLineWidth (Width_t lwidth) |
| Set the line width. | |
 Public Member Functions inherited from TAttFill Public Member Functions inherited from TAttFill | |
| TAttFill () | |
| AttFill default constructor. | |
| TAttFill (Color_t fcolor, Style_t fstyle) | |
| AttFill normal constructor. | |
| virtual | ~TAttFill () |
| AttFill destructor. | |
| void | Copy (TAttFill &attfill) const |
| Copy this fill attributes to a new TAttFill. | |
| virtual Color_t | GetFillColor () const |
| Return the fill area color. | |
| virtual Style_t | GetFillStyle () const |
| Return the fill area style. | |
| virtual Bool_t | IsTransparent () const |
| virtual void | Modify () |
| Change current fill area attributes if necessary. | |
| virtual void | ResetAttFill (Option_t *option="") |
| Reset this fill attributes to default values. | |
| virtual void | SaveFillAttributes (std::ostream &out, const char *name, Int_t coldef=1, Int_t stydef=1001) |
| Save fill attributes as C++ statement(s) on output stream out. | |
| virtual void | SetFillAttributes () |
| Invoke the DialogCanvas Fill attributes. | |
| virtual void | SetFillColor (Color_t fcolor) |
| Set the fill area color. | |
| virtual void | SetFillColorAlpha (Color_t fcolor, Float_t falpha) |
| Set a transparent fill color. | |
| virtual void | SetFillStyle (Style_t fstyle) |
| Set the fill area style. | |
 Public Member Functions inherited from TAttMarker Public Member Functions inherited from TAttMarker | |
| TAttMarker () | |
| TAttMarker default constructor. | |
| TAttMarker (Color_t color, Style_t style, Size_t msize) | |
| TAttMarker normal constructor. | |
| virtual | ~TAttMarker () |
| TAttMarker destructor. | |
| void | Copy (TAttMarker &attmarker) const |
| Copy this marker attributes to a new TAttMarker. | |
| virtual Color_t | GetMarkerColor () const |
| Return the marker color. | |
| virtual Size_t | GetMarkerSize () const |
| Return the marker size. | |
| virtual Style_t | GetMarkerStyle () const |
| Return the marker style. | |
| virtual void | Modify () |
| Change current marker attributes if necessary. | |
| virtual void | ResetAttMarker (Option_t *toption="") |
| Reset this marker attributes to the default values. | |
| virtual void | SaveMarkerAttributes (std::ostream &out, const char *name, Int_t coldef=1, Int_t stydef=1, Int_t sizdef=1) |
| Save line attributes as C++ statement(s) on output stream out. | |
| virtual void | SetMarkerAttributes () |
| Invoke the DialogCanvas Marker attributes. | |
| virtual void | SetMarkerColor (Color_t mcolor=1) |
| Set the marker color. | |
| virtual void | SetMarkerColorAlpha (Color_t mcolor, Float_t malpha) |
| Set a transparent marker color. | |
| virtual void | SetMarkerSize (Size_t msize=1) |
| Set the marker size. | |
| virtual void | SetMarkerStyle (Style_t mstyle=1) |
| Set the marker style. | |
Static Public Member Functions | |
| static Double_t | AgrestiCoull (Double_t total, Double_t passed, Double_t level, Bool_t bUpper) |
| Calculates the boundaries for the frequentist Agresti-Coull interval. | |
| static Double_t | Bayesian (Double_t total, Double_t passed, Double_t level, Double_t alpha, Double_t beta, Bool_t bUpper, Bool_t bShortest=false) |
| Calculates the boundaries for a Bayesian confidence interval (shortest or central interval depending on the option) | |
| static Double_t | BetaCentralInterval (Double_t level, Double_t alpha, Double_t beta, Bool_t bUpper) |
| Calculates the boundaries for a central confidence interval for a Beta distribution. | |
| static Double_t | BetaMean (Double_t alpha, Double_t beta) |
| Compute the mean (average) of the beta distribution. | |
| static Double_t | BetaMode (Double_t alpha, Double_t beta) |
| Compute the mode of the beta distribution. | |
| static Bool_t | BetaShortestInterval (Double_t level, Double_t alpha, Double_t beta, Double_t &lower, Double_t &upper) |
| Calculates the boundaries for a shortest confidence interval for a Beta distribution. | |
| static Bool_t | CheckBinning (const TH1 &pass, const TH1 &total) |
| Checks binning for each axis. | |
| static Bool_t | CheckConsistency (const TH1 &pass, const TH1 &total, Option_t *opt="") |
| Checks the consistence of the given histograms. | |
| static Bool_t | CheckEntries (const TH1 &pass, const TH1 &total, Option_t *opt="") |
| Checks whether bin contents are compatible with binomial statistics. | |
| static Bool_t | CheckWeights (const TH1 &pass, const TH1 &total) |
| Check if both histogram are weighted. | |
| static Double_t | ClopperPearson (Double_t total, Double_t passed, Double_t level, Bool_t bUpper) |
| Calculates the boundaries for the frequentist Clopper-Pearson interval. | |
| static Double_t | Combine (Double_t &up, Double_t &low, Int_t n, const Int_t *pass, const Int_t *total, Double_t alpha, Double_t beta, Double_t level=0.683, const Double_t *w=0, Option_t *opt="") |
| static TGraphAsymmErrors * | Combine (TCollection *pList, Option_t *opt="", Int_t n=0, const Double_t *w=0) |
| Combines a list of 1-dimensional TEfficiency objects. | |
| static Double_t | FeldmanCousins (Double_t total, Double_t passed, Double_t level, Bool_t bUpper) |
| Calculates the boundaries for the frequentist Feldman-Cousins interval. | |
| static Bool_t | FeldmanCousinsInterval (Double_t total, Double_t passed, Double_t level, Double_t &lower, Double_t &upper) |
| Calculates the interval boundaries using the frequentist methods of Feldman-Cousins. | |
| static Double_t | MidPInterval (Double_t total, Double_t passed, Double_t level, Bool_t bUpper) |
| Calculates the boundaries using the mid-P binomial interval (Lancaster method) from B. | |
| static Double_t | Normal (Double_t total, Double_t passed, Double_t level, Bool_t bUpper) |
| Returns the confidence limits for the efficiency supposing that the efficiency follows a normal distribution with the rms below. | |
| static Double_t | Wilson (Double_t total, Double_t passed, Double_t level, Bool_t bUpper) |
| Calculates the boundaries for the frequentist Wilson interval. | |
 Static Public Member Functions inherited from TObject Static Public Member Functions inherited from TObject | |
| static Longptr_t | GetDtorOnly () |
| Return destructor only flag. | |
| static Bool_t | GetObjectStat () |
| Get status of object stat flag. | |
| static void | SetDtorOnly (void *obj) |
| Set destructor only flag. | |
| static void | SetObjectStat (Bool_t stat) |
| Turn on/off tracking of objects in the TObjectTable. | |
 Static Public Member Functions inherited from TAttMarker Static Public Member Functions inherited from TAttMarker | |
| static Width_t | GetMarkerLineWidth (Style_t style) |
| Internal helper function that returns the line width of the given marker style (0 = filled marker) | |
| static Style_t | GetMarkerStyleBase (Style_t style) |
| Internal helper function that returns the corresponding marker style with line width 1 for the given style. | |
Protected Types | |
| enum | EStatusBits { kIsBayesian = BIT(14) , kPosteriorMode = BIT(15) , kShortestInterval = BIT(16) , kUseBinPrior = BIT(17) , kUseWeights = BIT(18) } |
 Protected Types inherited from TObject Protected Types inherited from TObject | |
| enum | { kOnlyPrepStep = BIT(3) } |
Protected Member Functions | |
| void | Build (const char *name, const char *title) |
| Building standard data structure of a TEfficiency object. | |
| void | FillGraph (TGraphAsymmErrors *graph, Option_t *opt) const |
| Fill the graph to be painted with information from TEfficiency Internal method called by TEfficiency::Paint or TEfficiency::CreateGraph. | |
| void | FillHistogram (TH2 *h2) const |
| Fill the 2d histogram to be painted with information from TEfficiency 2D Internal method called by TEfficiency::Paint or TEfficiency::CreatePaintingGraph. | |
 Protected Member Functions inherited from TObject Protected Member Functions inherited from TObject | |
| virtual void | DoError (int level, const char *location, const char *fmt, va_list va) const |
| Interface to ErrorHandler (protected). | |
| void | MakeZombie () |
Protected Attributes | |
| Double_t | fBeta_alpha |
| Global parameter for prior beta distribution (default = 1) | |
| Double_t | fBeta_beta |
| Global parameter for prior beta distribution (default = 1) | |
| std::vector< std::pair< Double_t, Double_t > > | fBeta_bin_params |
| Parameter for prior beta distribution different bin by bin (default vector is empty) | |
| Double_t(* | fBoundary )(Double_t, Double_t, Double_t, Bool_t) |
| ! Pointer to a method calculating the boundaries of confidence intervals | |
| Double_t | fConfLevel |
| Confidence level (default = 0.683, 1 sigma) | |
| TDirectory * | fDirectory |
| ! Pointer to directory holding this TEfficiency object | |
| TList * | fFunctions |
| ->Pointer to list of functions | |
| TGraphAsymmErrors * | fPaintGraph |
| ! Temporary graph for painting | |
| TH2 * | fPaintHisto |
| ! Temporary histogram for painting | |
| TH1 * | fPassedHistogram |
| Histogram for events which passed certain criteria. | |
| EStatOption | fStatisticOption |
| Defines how the confidence intervals are determined. | |
| TH1 * | fTotalHistogram |
| Histogram for total number of events. | |
| Double_t | fWeight |
| Weight for all events (default = 1) | |
 Protected Attributes inherited from TNamed Protected Attributes inherited from TNamed | |
| TString | fName |
| TString | fTitle |
 Protected Attributes inherited from TAttLine Protected Attributes inherited from TAttLine | |
| Color_t | fLineColor |
| Line color. | |
| Style_t | fLineStyle |
| Line style. | |
| Width_t | fLineWidth |
| Line width. | |
 Protected Attributes inherited from TAttFill Protected Attributes inherited from TAttFill | |
| Color_t | fFillColor |
| Fill area color. | |
| Style_t | fFillStyle |
| Fill area style. | |
 Protected Attributes inherited from TAttMarker Protected Attributes inherited from TAttMarker | |
| Color_t | fMarkerColor |
| Marker color. | |
| Size_t | fMarkerSize |
| Marker size. | |
| Style_t | fMarkerStyle |
| Marker style. | |
#include <TEfficiency.h>
Enumeration type for different statistic options for calculating confidence intervals kF* ... frequentist methods; kB* ... bayesian methods.
Definition at line 32 of file TEfficiency.h.
|
protected |
Definition at line 61 of file TEfficiency.h.
| TEfficiency::TEfficiency | ( | ) |
Constructor using two existing histograms as input.
Input: passed - contains the events fulfilling some criteria total - contains all investigated events
Notes: - both histograms have to fulfill the conditions of CheckConsistency
Definition at line 657 of file TEfficiency.cxx.
| TEfficiency::TEfficiency | ( | const char * | name, |
| const char * | title, | ||
| Int_t | nbins, | ||
| const Double_t * | xbins | ||
| ) |
Create 1-dimensional TEfficiency object with variable bin size.
Constructor creates two new and empty histograms with a given binning
Input:
name: the common part of the name for both histograms (no blanks) fTotalHistogram has name: name + "_total" fPassedHistogram has name: name + "_passed"title: the common part of the title for both histogram fTotalHistogram has title: title + " (total)" fPassedHistogram has title: title + " (passed)" It is possible to label the axis by passing a title with the following format: "title;xlabel;ylabel".nbins: number of bins on the x-axisxbins: array of length (nbins + 1) with low-edges for each bin xbins[nbinsx] ... lower edge for overflow bin Definition at line 723 of file TEfficiency.cxx.
| TEfficiency::TEfficiency | ( | const char * | name, |
| const char * | title, | ||
| Int_t | nbinsx, | ||
| Double_t | xlow, | ||
| Double_t | xup | ||
| ) |
Create 1-dimensional TEfficiency object with fixed bins size.
Constructor creates two new and empty histograms with a fixed binning.
Input:
name: the common part of the name for both histograms(no blanks) fTotalHistogram has name: name + "_total" fPassedHistogram has name: name + "_passed"title: the common part of the title for both histogram fTotalHistogram has title: title + " (total)" fPassedHistogram has title: title + " (passed)" It is possible to label the axis by passing a title with the following format: "title;xlabel;ylabel".nbinsx: number of bins on the x-axisxlow: lower edge of first binxup: upper edge of last bin Definition at line 764 of file TEfficiency.cxx.
| TEfficiency::TEfficiency | ( | const char * | name, |
| const char * | title, | ||
| Int_t | nbinsx, | ||
| Double_t | xlow, | ||
| Double_t | xup, | ||
| Int_t | nbinsy, | ||
| Double_t | ylow, | ||
| Double_t | yup | ||
| ) |
Create 2-dimensional TEfficiency object with fixed bin size.
Constructor creates two new and empty histograms with a fixed binning.
Input:
name: the common part of the name for both histograms(no blanks) fTotalHistogram has name: name + "_total" fPassedHistogram has name: name + "_passed"title: the common part of the title for both histogram fTotalHistogram has title: title + " (total)" fPassedHistogram has title: title + " (passed)" It is possible to label the axis by passing a title with the following format: "title;xlabel;ylabel;zlabel".nbinsx: number of bins on the x-axisxlow: lower edge of first x-binxup: upper edge of last x-binnbinsy: number of bins on the y-axisylow: lower edge of first y-binyup: upper edge of last y-bin Definition at line 806 of file TEfficiency.cxx.
| TEfficiency::TEfficiency | ( | const char * | name, |
| const char * | title, | ||
| Int_t | nbinsx, | ||
| const Double_t * | xbins, | ||
| Int_t | nbinsy, | ||
| const Double_t * | ybins | ||
| ) |
Create 2-dimensional TEfficiency object with variable bin size.
Constructor creates two new and empty histograms with a given binning.
Input:
name: the common part of the name for both histograms(no blanks) fTotalHistogram has name: name + "_total" fPassedHistogram has name: name + "_passed"title: the common part of the title for both histogram fTotalHistogram has title: title + " (total)" fPassedHistogram has title: title + " (passed)" It is possible to label the axis by passing a title with the following format: "title;xlabel;ylabel;zlabel".nbinsx: number of bins on the x-axisxbins: array of length (nbins + 1) with low-edges for each bin xbins[nbinsx] ... lower edge for overflow x-binnbinsy: number of bins on the y-axisybins: array of length (nbins + 1) with low-edges for each bin ybins[nbinsy] ... lower edge for overflow y-bin Definition at line 849 of file TEfficiency.cxx.
| TEfficiency::TEfficiency | ( | const char * | name, |
| const char * | title, | ||
| Int_t | nbinsx, | ||
| Double_t | xlow, | ||
| Double_t | xup, | ||
| Int_t | nbinsy, | ||
| Double_t | ylow, | ||
| Double_t | yup, | ||
| Int_t | nbinsz, | ||
| Double_t | zlow, | ||
| Double_t | zup | ||
| ) |
Create 3-dimensional TEfficiency object with fixed bin size.
Constructor creates two new and empty histograms with a fixed binning.
Input:
name: the common part of the name for both histograms(no blanks) fTotalHistogram has name: name + "_total" fPassedHistogram has name: name + "_passed"title: the common part of the title for both histogram fTotalHistogram has title: title + " (total)" fPassedHistogram has title: title + " (passed)" It is possible to label the axis by passing a title with the following format: "title;xlabel;ylabel;zlabel".nbinsx: number of bins on the x-axisxlow: lower edge of first x-binxup: upper edge of last x-binnbinsy: number of bins on the y-axisylow: lower edge of first y-binyup: upper edge of last y-binnbinsz: number of bins on the z-axiszlow: lower edge of first z-binzup: upper edge of last z-bin Definition at line 895 of file TEfficiency.cxx.
| TEfficiency::TEfficiency | ( | const char * | name, |
| const char * | title, | ||
| Int_t | nbinsx, | ||
| const Double_t * | xbins, | ||
| Int_t | nbinsy, | ||
| const Double_t * | ybins, | ||
| Int_t | nbinsz, | ||
| const Double_t * | zbins | ||
| ) |
Create 3-dimensional TEfficiency object with variable bin size.
Constructor creates two new and empty histograms with a given binning.
Input:
name: the common part of the name for both histograms(no blanks) fTotalHistogram has name: name + "_total" fPassedHistogram has name: name + "_passed"title: the common part of the title for both histogram fTotalHistogram has title: title + " (total)" fPassedHistogram has title: title + " (passed)" It is possible to label the axis by passing a title with the following format: "title;xlabel;ylabel;zlabel".nbinsx: number of bins on the x-axisxbins: array of length (nbins + 1) with low-edges for each bin xbins[nbinsx] ... lower edge for overflow x-binnbinsy: number of bins on the y-axisybins: array of length (nbins + 1) with low-edges for each bin xbins[nbinsx] ... lower edge for overflow y-binnbinsz: number of bins on the z-axiszbins: array of length (nbins + 1) with low-edges for each bin xbins[nbinsx] ... lower edge for overflow z-bin Definition at line 942 of file TEfficiency.cxx.
| TEfficiency::TEfficiency | ( | const TEfficiency & | rEff | ) |
Copy constructor.
The list of associated objects (e.g. fitted functions) is not copied.
Note:
Definition at line 981 of file TEfficiency.cxx.
| TEfficiency::~TEfficiency | ( | ) |
default destructor
Definition at line 1026 of file TEfficiency.cxx.
|
inline |
Definition at line 94 of file TEfficiency.h.
|
static |
Calculates the boundaries for the frequentist Agresti-Coull interval.
| total | number of total events |
| passed | 0 <= number of passed events <= total |
| level | confidence level |
| bUpper | true - upper boundary is returned false - lower boundary is returned |
\begin{eqnarray*} \alpha &=& 1 - \frac{level}{2} \\ \kappa &=& \Phi^{-1}(1 - \alpha,1)\ ... normal\ quantile\ function\\ mode &=& \frac{passed + \frac{\kappa^{2}}{2}}{total + \kappa^{2}}\\ \Delta &=& \kappa * \sqrt{\frac{mode * (1 - mode)}{total + \kappa^{2}}}\\ return &=& max(0,mode - \Delta)\ or\ min(1,mode + \Delta) \end{eqnarray*}
Definition at line 1076 of file TEfficiency.cxx.
|
static |
Calculates the boundaries for a Bayesian confidence interval (shortest or central interval depending on the option)
| [in] | total | number of total events |
| [in] | passed | 0 <= number of passed events <= total |
| [in] | level | confidence level |
| [in] | alpha | shape parameter > 0 for the prior distribution (fBeta_alpha) |
| [in] | beta | shape parameter > 0 for the prior distribution (fBeta_beta) |
| [in] | bUpper |
|
| [in] | bShortest | ?? |
Note: In the case central confidence interval is calculated. when passed = 0 (or passed = total) the lower (or upper) interval values will be larger than 0 (or smaller than 1).
Calculation:
The posterior probability in bayesian statistics is given by:
\[ P(\varepsilon |k,N) \propto L(\varepsilon|k,N) \times Prior(\varepsilon) \]
As an efficiency can be interpreted as probability of a positive outcome of a Bernoullli trial the likelihood function is given by the binomial distribution:
\[ L(\varepsilon|k,N) = Binomial(N,k) \varepsilon ^{k} (1 - \varepsilon)^{N-k} \]
At the moment only beta distributions are supported as prior probabilities of the efficiency ( \( B(\alpha,\beta)\) is the beta function):
\[ Prior(\varepsilon) = \frac{1}{B(\alpha,\beta)} \varepsilon ^{\alpha - 1} (1 - \varepsilon)^{\beta - 1} \]
The posterior probability is therefore again given by a beta distribution:
\[ P(\varepsilon |k,N) \propto \varepsilon ^{k + \alpha - 1} (1 - \varepsilon)^{N - k + \beta - 1} \]
In case of central intervals the lower boundary for the equal-tailed confidence interval is given by the inverse cumulative (= quantile) function for the quantile \( \frac{1 - level}{2} \). The upper boundary for the equal-tailed confidence interval is given by the inverse cumulative (= quantile) function for the quantile \( \frac{1 + level}{2} \). Hence it is the solution \( \varepsilon \) of the following equation:
\[ I_{\varepsilon}(k + \alpha,N - k + \beta) = \frac{1}{norm} \int_{0}^{\varepsilon} dt t^{k + \alpha - 1} (1 - t)^{N - k + \beta - 1} = \frac{1 \pm level}{2} \]
In the case of shortest interval the minimum interval around the mode is found by minimizing the length of all intervals width the given probability content. See TEfficiency::BetaShortestInterval
Definition at line 1251 of file TEfficiency.cxx.
|
static |
Calculates the boundaries for a central confidence interval for a Beta distribution.
| [in] | level | confidence level |
| [in] | a | parameter > 0 for the beta distribution (for a posterior is passed + prior_alpha |
| [in] | b | parameter > 0 for the beta distribution (for a posterior is (total-passed) + prior_beta |
| [in] | bUpper | true - upper boundary is returned false - lower boundary is returned |
Definition at line 1275 of file TEfficiency.cxx.
Compute the mean (average) of the beta distribution.
| [in] | a | parameter > 0 for the beta distribution (for a posterior is passed + prior_alpha |
| [in] | b | parameter > 0 for the beta distribution (for a posterior is (total-passed) + prior_beta |
Definition at line 1385 of file TEfficiency.cxx.
Compute the mode of the beta distribution.
| [in] | a | parameter > 0 for the beta distribution (for a posterior is passed + prior_alpha |
| [in] | b | parameter > 0 for the beta distribution (for a posterior is (total-passed) + prior_beta |
note the mode is defined for a Beta(a,b) only if (a,b)>1 (a = passed+alpha; b = total-passed+beta) return then the following in case (a,b) < 1:
Definition at line 1408 of file TEfficiency.cxx.
|
static |
Calculates the boundaries for a shortest confidence interval for a Beta distribution.
| [in] | level | confidence level |
| [in] | a | parameter > 0 for the beta distribution (for a posterior is passed + prior_alpha |
| [in] | b | parameter > 0 for the beta distribution (for a posterior is (total-passed) + prior_beta |
| [out] | upper | upper boundary is returned |
| [out] | lower | lower boundary is returned |
The lower/upper boundary are then obtained by finding the shortest interval of the beta distribution contained the desired probability level. The length of all possible intervals is minimized in order to find the shortest one
Definition at line 1331 of file TEfficiency.cxx.
Browse object. May be overridden for another default action.
Reimplemented from TObject.
Definition at line 95 of file TEfficiency.h.
|
protected |
Building standard data structure of a TEfficiency object.
Notes:
Definition at line 1432 of file TEfficiency.cxx.
Checks binning for each axis.
It is assumed that the passed histograms have the same dimension.
Definition at line 1454 of file TEfficiency.cxx.
|
static |
Checks the consistence of the given histograms.
The histograms are considered as consistent if:
Definition at line 1503 of file TEfficiency.cxx.
|
static |
Checks whether bin contents are compatible with binomial statistics.
The following inequality has to be valid for each bin i: total.GetBinContent(i) >= pass.GetBinContent(i)
Note:
Definition at line 1535 of file TEfficiency.cxx.
Check if both histogram are weighted.
If they are weighted a true is returned
Definition at line 1565 of file TEfficiency.cxx.
|
static |
Calculates the boundaries for the frequentist Clopper-Pearson interval.
This interval is recommended by the PDG.
| [in] | total | number of total events |
| [in] | passed | 0 <= number of passed events <= total |
| [in] | level | confidence level |
| [in] | bUpper | true - upper boundary is returned ;false - lower boundary is returned |
Calculation:
The lower boundary of the Clopper-Pearson interval is the "exact" inversion of the test:
\begin{eqnarray*} P(x \geq passed; total) &=& \frac{1 - level}{2}\\ P(x \geq passed; total) &=& 1 - P(x \leq passed - 1; total)\\ &=& 1 - \frac{1}{norm} * \int_{0}^{1 - \varepsilon} t^{total - passed} (1 - t)^{passed - 1} dt\\ &=& 1 - \frac{1}{norm} * \int_{\varepsilon}^{1} t^{passed - 1} (1 - t)^{total - passed} dt\\ &=& \frac{1}{norm} * \int_{0}^{\varepsilon} t^{passed - 1} (1 - t)^{total - passed} dt\\ &=& I_{\varepsilon}(passed,total - passed + 1) \end{eqnarray*}
The lower boundary is therefore given by the \( \frac{1 - level}{2}\) quantile of the beta distribution.
The upper boundary of the Clopper-Pearson interval is the "exact" inversion of the test:
\begin{eqnarray*} P(x \leq passed; total) &=& \frac{1 - level}{2}\\ P(x \leq passed; total) &=& \frac{1}{norm} * \int_{0}^{1 - \varepsilon} t^{total - passed - 1} (1 - t)^{passed} dt\\ &=& \frac{1}{norm} * \int_{\varepsilon}^{1} t^{passed} (1 - t)^{total - passed - 1} dt\\ &=& 1 - \frac{1}{norm} * \int_{0}^{\varepsilon} t^{passed} (1 - t)^{total - passed - 1} dt\\ \Rightarrow 1 - \frac{1 - level}{2} &=& \frac{1}{norm} * \int_{0}^{\varepsilon} t^{passed} (1 - t)^{total - passed -1} dt\\ \frac{1 + level}{2} &=& I_{\varepsilon}(passed + 1,total - passed) \end{eqnarray*}
The upper boundary is therefore given by the \(\frac{1 + level}{2}\) quantile of the beta distribution.
Note: The connection between the binomial distribution and the regularized incomplete beta function \( I_{\varepsilon}(\alpha,\beta)\) has been used.
Definition at line 1823 of file TEfficiency.cxx.
|
static |
Calculates the combined efficiency and its uncertainties
This method does a bayesian combination of the given samples.
\param[in] up contains the upper limit of the confidence interval afterwards
\param[in] low contains the lower limit of the confidence interval afterwards
\param[in] n number of samples which are combined
\param[in] pass array of length n containing the number of passed events
\param[in] total array of length n containing the corresponding numbers of total events
\param[in] alpha shape parameters for the beta distribution as prior
\param[in] beta shape parameters for the beta distribution as prior
\param[in] level desired confidence level
\param[in] w weights for each sample; if not given, all samples get the weight 1
The weights do not need to be normalized, since they are internally renormalized
to the number of effective entries.
\param[in] opt
- mode : The mode is returned instead of the mean of the posterior as best value
When using the mode the shortest interval is also computed instead of the central one
- shortest: compute shortest interval (done by default if mode option is set)
- central: compute central interval (done by default if mode option is NOT set)
Calculation:
The combined posterior distributions is calculated from the Bayes theorem assuming a common prior Beta distribution.
It is easy to proof that the combined posterior is then:
\begin{eqnarray*} P_{comb}(\epsilon |{w_{i}}; {k_{i}}; {N_{i}}) &=& B(\epsilon, \sum_{i}{ w_{i} k_{i}} + \alpha, \sum_{i}{ w_{i}(n_{i}-k_{i})}+\beta)\\ w_{i} &=& weight\ for\ each\ sample\ renormalized\ to\ the\ effective\ entries\\ w^{'}_{i} &=& w_{i} \frac{ \sum_{i} {w_{i} } } { \sum_{i} {w_{i}^{2} } } \end{eqnarray*}
The estimated efficiency is the mode (or the mean) of the obtained posterior distribution
The boundaries of the confidence interval for a confidence level (1 - a) are given by the a/2 and 1-a/2 quantiles of the resulting cumulative distribution.
Example (uniform prior distribution):

Definition at line 1919 of file TEfficiency.cxx.
|
static |
Combines a list of 1-dimensional TEfficiency objects.
A TGraphAsymmErrors object is returned which contains the estimated efficiency and its uncertainty for each bin. If the combination fails, a zero pointer is returned.
At the moment the combining is only implemented for bayesian statistics.
| [in] | pList | list containing TEfficiency objects which should be combined only one-dimensional efficiencies are taken into account |
| [in] | option |
|
| [in] | n | number of weights (has to be the number of one-dimensional TEfficiency objects in pList) If no weights are passed, the internal weights GetWeight() of the given TEfficiency objects are used. |
| [in] | w | array of length n with weights for each TEfficiency object in pList (w[0] correspond to pList->First ... w[n-1] -> pList->Last) The weights do not have to be normalised. |
For each bin the calculation is done by the Combine(double&, double& ...) method.
Definition at line 2009 of file TEfficiency.cxx.
| TGraphAsymmErrors * TEfficiency::CreateGraph | ( | Option_t * | opt = "" | ) | const |
Create the graph used be painted (for dim=1 TEfficiency) The return object is managed by the caller.
Definition at line 1594 of file TEfficiency.cxx.
Create the histogram used to be painted (for dim=2 TEfficiency) The return object is managed by the caller.
Definition at line 1699 of file TEfficiency.cxx.
Compute distance from point px,py to a graph.
Compute the closest distance of approach from point px,py to this line. The distance is computed in pixels units.
Forward the call to the painted graph
Reimplemented from TObject.
Definition at line 2194 of file TEfficiency.cxx.
Draws the current TEfficiency object.
| [in] | opt |
|
Specific TEfficiency drawing options:
Reimplemented from TObject.
Definition at line 2215 of file TEfficiency.cxx.
Execute action corresponding to one event.
This member function is called when the drawn class is clicked with the locator If Left button clicked on one of the line end points, this point follows the cursor until button is released.
if Middle button clicked, the line is moved parallel to itself until the button is released. Forward the call to the underlying graph
Reimplemented from TObject.
Definition at line 2249 of file TEfficiency.cxx.
|
static |
Calculates the boundaries for the frequentist Feldman-Cousins interval.
| total | number of total events |
| passed | 0 <= number of passed events <= total |
| level | confidence level |
| bUpper | true - upper boundary is returned false - lower boundary is returned |
Definition at line 1099 of file TEfficiency.cxx.
|
static |
Calculates the interval boundaries using the frequentist methods of Feldman-Cousins.
| [in] | total | number of total events |
| [in] | passed | 0 <= number of passed events <= total |
| [in] | level | confidence level |
| [out] | lower | lower boundary returned on exit |
| [out] | upper | lower boundary returned on exit |
Calculation:
The Feldman-Cousins is a frequentist method where the interval is estimated using a Neyman construction where the ordering is based on the likelihood ratio:
\[ LR = \frac{Binomial(k | N, \epsilon)}{Binomial(k | N, \hat{\epsilon} ) } \]
See G. J. Feldman and R. D. Cousins, Phys. Rev. D57 (1998) 3873 and R. D. Cousins, K. E. Hymes, J. Tucker, Nuclear Instruments and Methods in Physics Research A 612 (2010) 388
Implemented using classes developed by Jordan Tucker and Luca Lista See File hist/hist/src/TEfficiencyHelper.h
Definition at line 1132 of file TEfficiency.cxx.
This function is used for filling the two histograms.
| [in] | bPassed | flag whether the current event passed the selection
|
| [in] | x | x-value |
| [in] | y | y-value (use default=0 for 1-D efficiencies) |
| [in] | z | z-value (use default=0 for 2-D or 1-D efficiencies) |
Definition at line 2265 of file TEfficiency.cxx.
|
protected |
Fill the graph to be painted with information from TEfficiency Internal method called by TEfficiency::Paint or TEfficiency::CreateGraph.
Definition at line 1615 of file TEfficiency.cxx.
Fill the 2d histogram to be painted with information from TEfficiency 2D Internal method called by TEfficiency::Paint or TEfficiency::CreatePaintingGraph.
Definition at line 1737 of file TEfficiency.cxx.
| void TEfficiency::FillWeighted | ( | Bool_t | bPassed, |
| Double_t | weight, | ||
| Double_t | x, | ||
| Double_t | y = 0, |
||
| Double_t | z = 0 |
||
| ) |
This function is used for filling the two histograms with a weight.
| [in] | bPassed | flag whether the current event passed the selection
|
| [in] | weight | weight for the event |
| [in] | x | x-value |
| [in] | y | y-value (use default=0 for 1-D efficiencies) |
| [in] | z | z-value (use default=0 for 2-D or 1-D efficiencies) |
Note: - this function will call SetUseWeightedEvents if it was not called by the user before
Definition at line 2299 of file TEfficiency.cxx.
Returns the global bin number containing the given values.
Note:
Definition at line 2335 of file TEfficiency.cxx.
| TFitResultPtr TEfficiency::Fit | ( | TF1 * | f1, |
| Option_t * | opt = "" |
||
| ) |
Fits the efficiency using the TBinomialEfficiencyFitter class.
The resulting fit function is added to the list of associated functions.
Options:
Definition at line 2359 of file TEfficiency.cxx.
Definition at line 106 of file TEfficiency.h.
Definition at line 107 of file TEfficiency.h.
|
inline |
Definition at line 108 of file TEfficiency.h.
| TH1 * TEfficiency::GetCopyPassedHisto | ( | ) | const |
Returns a cloned version of fPassedHistogram.
Notes:
Definition at line 2420 of file TEfficiency.cxx.
| TH1 * TEfficiency::GetCopyTotalHisto | ( | ) | const |
Returns a cloned version of fTotalHistogram.
Notes:
Definition at line 2450 of file TEfficiency.cxx.
| Int_t TEfficiency::GetDimension | ( | ) | const |
returns the dimension of the current TEfficiency object
Definition at line 2462 of file TEfficiency.cxx.
|
inline |
Definition at line 112 of file TEfficiency.h.
Returns the efficiency in the given global bin.
Note:
Definition at line 2484 of file TEfficiency.cxx.
Returns the lower error on the efficiency in the given global bin.
The result depends on the current confidence level fConfLevel and the chosen statistic option fStatisticOption. See SetStatisticOption(Int_t) for more details.
Note: If the histograms are filled with weights, only bayesian methods and the normal approximation are supported.
Definition at line 2535 of file TEfficiency.cxx.
Returns the upper error on the efficiency in the given global bin.
The result depends on the current confidence level fConfLevel and the chosen statistic option fStatisticOption. See SetStatisticOption(Int_t) for more details.
Note: If the histograms are filled with weights, only bayesian methods and the normal approximation are supported.
Definition at line 2615 of file TEfficiency.cxx.
Returns the global bin number which can be used as argument for the following functions:
see TH1::GetBin() for conventions on numbering bins
Definition at line 2693 of file TEfficiency.cxx.
| TList * TEfficiency::GetListOfFunctions | ( | ) |
Definition at line 2700 of file TEfficiency.cxx.
|
inline |
Definition at line 117 of file TEfficiency.h.
|
inline |
Definition at line 118 of file TEfficiency.h.
|
inline |
Definition at line 120 of file TEfficiency.h.
|
inline |
Definition at line 121 of file TEfficiency.h.
|
inline |
Definition at line 122 of file TEfficiency.h.
|
inline |
Definition at line 123 of file TEfficiency.h.
| Long64_t TEfficiency::Merge | ( | TCollection * | pList | ) |
Merges the TEfficiency objects in the given list to the given TEfficiency object using the operator+=(TEfficiency&)
The merged result is stored in the current object. The statistic options and the confidence level are taken from the current object.
This function should be used when all TEfficiency objects correspond to the same process.
The new weight is set according to: \( \frac{1}{w_{new}} = \sum_{i} \frac{1}{w_{i}} \)
Definition at line 2718 of file TEfficiency.cxx.
|
static |
Calculates the boundaries using the mid-P binomial interval (Lancaster method) from B.
Cousing and J. Tucker. See http://arxiv.org/abs/0905.3831 for a description and references for the method
Modify equal_tailed to get the kind of interval you want. Can also be converted to interval on ratio of poisson means X/Y by the substitutions
Definition at line 1157 of file TEfficiency.cxx.
|
static |
Returns the confidence limits for the efficiency supposing that the efficiency follows a normal distribution with the rms below.
| [in] | total | number of total events |
| [in] | passed | 0 <= number of passed events <= total |
| [in] | level | confidence level |
| [in] | bUpper |
|
Calculation:
\begin{eqnarray*} \hat{\varepsilon} &=& \frac{passed}{total}\\ \sigma_{\varepsilon} &=& \sqrt{\frac{\hat{\varepsilon} (1 - \hat{\varepsilon})}{total}}\\ \varepsilon_{low} &=& \hat{\varepsilon} \pm \Phi^{-1}(\frac{level}{2},\sigma_{\varepsilon}) \end{eqnarray*}
Definition at line 2755 of file TEfficiency.cxx.
| TEfficiency & TEfficiency::operator+= | ( | const TEfficiency & | rhs | ) |
Adds the histograms of another TEfficiency object to current histograms.
The statistic options and the confidence level remain unchanged.
fTotalHistogram += rhs.fTotalHistogram; fPassedHistogram += rhs.fPassedHistogram;
calculates a new weight: current weight of this TEfficiency object = \( w_{1} \) weight of rhs = \( w_{2} \) \( w_{new} = \frac{w_{1} \times w_{2}}{w_{1} + w_{2}} \)
Definition at line 2782 of file TEfficiency.cxx.
| TEfficiency & TEfficiency::operator= | ( | const TEfficiency & | rhs | ) |
Assignment operator.
The histograms, statistic option, confidence level, weight and paint styles of rhs are copied to the this TEfficiency object.
Note: - The list of associated functions is not copied. After this operation the list of associated functions is empty.
Definition at line 2824 of file TEfficiency.cxx.
Paints this TEfficiency object.
For details on the possible option see Draw(Option_t*)
Note for 1D classes In 1D the TEfficiency uses a TGraphAsymmErrors for drawing The TGraph is created only the first time Paint is used. The user can manipulate the TGraph via the method TEfficiency::GetPaintedGraph() The TGraph creates behing an histogram for the axis. The histogram is created also only the first time. If the axis needs to be updated because in the meantime the class changed use this trick which will trigger a re-calculation of the axis of the graph TEfficiency::GetPaintedGraph()->Set(0)
Note that in order to access the painted graph via GetPaintedGraph() you need either to call Paint or better gPad->Update();
Reimplemented from TObject.
Definition at line 2882 of file TEfficiency.cxx.
Have histograms fixed bins along each axis?
Reimplemented from TObject.
Definition at line 2939 of file TEfficiency.cxx.
Sets the shape parameter α.
The prior probability of the efficiency is given by the beta distribution:
\[ f(\varepsilon;\alpha;\beta) = \frac{1}{B(\alpha,\beta)} \varepsilon^{\alpha-1} (1 - \varepsilon)^{\beta-1} \]
Note: - both shape parameters have to be positive (i.e. > 0)
Definition at line 3113 of file TEfficiency.cxx.
Sets the shape parameter β.
The prior probability of the efficiency is given by the beta distribution:
\[ f(\varepsilon;\alpha,\beta) = \frac{1}{B(\alpha,\beta)} \varepsilon^{\alpha-1} (1 - \varepsilon)^{\beta-1} \]
Note: - both shape parameters have to be positive (i.e. > 0)
Definition at line 3131 of file TEfficiency.cxx.
Sets different shape parameter α and β for the prior distribution for each bin.
By default the global parameter are used if they are not set for the specific bin The prior probability of the efficiency is given by the beta distribution:
\[ f(\varepsilon;\alpha;\beta) = \frac{1}{B(\alpha,\beta)} \varepsilon^{\alpha-1} (1 - \varepsilon)^{\beta-1} \]
Note:
Definition at line 3152 of file TEfficiency.cxx.
Set the bins for the underlined passed and total histograms If the class have been already filled the previous contents will be lost.
Definition at line 3193 of file TEfficiency.cxx.
Set the bins for the underlined passed and total histograms If the class have been already filled the previous contents will be lost.
Definition at line 3233 of file TEfficiency.cxx.
| Bool_t TEfficiency::SetBins | ( | Int_t | nx, |
| const Double_t * | xBins, | ||
| Int_t | ny, | ||
| const Double_t * | yBins, | ||
| Int_t | nz, | ||
| const Double_t * | zBins | ||
| ) |
Set the bins for the underlined passed and total histograms If the class have been already filled the previous contents will be lost.
Definition at line 3274 of file TEfficiency.cxx.
Set the bins for the underlined passed and total histograms If the class have been already filled the previous contents will be lost.
Definition at line 3173 of file TEfficiency.cxx.
| Bool_t TEfficiency::SetBins | ( | Int_t | nx, |
| Double_t | xmin, | ||
| Double_t | xmax, | ||
| Int_t | ny, | ||
| Double_t | ymin, | ||
| Double_t | ymax | ||
| ) |
Set the bins for the underlined passed and total histograms If the class have been already filled the previous contents will be lost.
Definition at line 3213 of file TEfficiency.cxx.
| Bool_t TEfficiency::SetBins | ( | Int_t | nx, |
| Double_t | xmin, | ||
| Double_t | xmax, | ||
| Int_t | ny, | ||
| Double_t | ymin, | ||
| Double_t | ymax, | ||
| Int_t | nz, | ||
| Double_t | zmin, | ||
| Double_t | zmax | ||
| ) |
Set the bins for the underlined passed and total histograms If the class have been already filled the previous contents will be lost.
Definition at line 3253 of file TEfficiency.cxx.
Definition at line 140 of file TEfficiency.h.
Sets the confidence level (0 < level < 1) The default value is 1-sigma :~ 0.683.
Definition at line 3295 of file TEfficiency.cxx.
| void TEfficiency::SetDirectory | ( | TDirectory * | dir | ) |
Sets the directory holding this TEfficiency object.
A reference to this TEfficiency object is removed from the current directory (if it exists) and a new reference to this TEfficiency object is added to the given directory.
Notes: - If the given directory is 0, the TEfficiency object does not belong to any directory and will not be written to file during the next TFile::Write() command.
Definition at line 3314 of file TEfficiency.cxx.
|
virtual |
Sets the name.
Note: The names of the internal histograms are set to "name + _total" and "name + _passed" respectively.
Reimplemented from TNamed.
Definition at line 3331 of file TEfficiency.cxx.
Sets the number of passed events in the given global bin.
returns "true" if the number of passed events has been updated otherwise "false" ist returned
Note: - requires: 0 <= events <= fTotalHistogram->GetBinContent(bin)
Definition at line 3350 of file TEfficiency.cxx.
Sets the histogram containing the passed events.
The given histogram is cloned and stored internally as histogram containing the passed events. The given histogram has to be consistent with the current fTotalHistogram (see CheckConsistency(const TH1&,const TH1&)). The method returns whether the fPassedHistogram has been replaced (true) or not (false).
Note: The list of associated functions fFunctions is cleared.
Option:
Definition at line 3381 of file TEfficiency.cxx.
Definition at line 138 of file TEfficiency.h.
Definition at line 137 of file TEfficiency.h.
Definition at line 139 of file TEfficiency.h.
| void TEfficiency::SetStatisticOption | ( | EStatOption | option | ) |
Sets the statistic option which affects the calculation of the confidence interval.
Options:
Definition at line 3446 of file TEfficiency.cxx.
|
virtual |
Sets the title.
Notes:
Example: Setting the title to "My Efficiency" and label the axis pEff->SetTitle("My Efficiency;x label;eff");
Reimplemented from TNamed.
Definition at line 3510 of file TEfficiency.cxx.
Sets the number of total events in the given global bin.
returns "true" if the number of total events has been updated otherwise "false" ist returned
Note: - requires: fPassedHistogram->GetBinContent(bin) <= events
Definition at line 3544 of file TEfficiency.cxx.
Sets the histogram containing all events.
The given histogram is cloned and stored internally as histogram containing all events. The given histogram has to be consistent with the current fPassedHistogram (see CheckConsistency(const TH1&,const TH1&)). The method returns whether the fTotalHistogram has been replaced (true) or not (false).
Note: The list of associated functions fFunctions is cleared.
Option:
Definition at line 3575 of file TEfficiency.cxx.
Definition at line 3609 of file TEfficiency.cxx.
Sets the global weight for this TEfficiency object.
Note: - weight has to be positive ( > 0)
Definition at line 3627 of file TEfficiency.cxx.
|
inline |
Definition at line 156 of file TEfficiency.h.
|
inline |
Definition at line 160 of file TEfficiency.h.
|
inline |
Definition at line 159 of file TEfficiency.h.
|
inline |
Definition at line 157 of file TEfficiency.h.
|
inline |
Definition at line 158 of file TEfficiency.h.
|
inline |
Definition at line 161 of file TEfficiency.h.
|
static |
Calculates the boundaries for the frequentist Wilson interval.
| [in] | total | number of total events |
| [in] | passed | 0 <= number of passed events <= total |
| [in] | level | confidence level |
| [in] | bUpper |
|
Calculation:
\begin{eqnarray*} \alpha &=& 1 - \frac{level}{2}\\ \kappa &=& \Phi^{-1}(1 - \alpha,1) ...\ normal\ quantile\ function\\ mode &=& \frac{passed + \frac{\kappa^{2}}{2}}{total + \kappa^{2}}\\ \Delta &=& \frac{\kappa}{total + \kappa^{2}} * \sqrt{passed (1 - \frac{passed}{total}) + \frac{\kappa^{2}}{4}}\\ return &=& max(0,mode - \Delta)\ or\ min(1,mode + \Delta) \end{eqnarray*}
Definition at line 3657 of file TEfficiency.cxx.
|
protected |
Global parameter for prior beta distribution (default = 1)
Definition at line 46 of file TEfficiency.h.
|
protected |
Global parameter for prior beta distribution (default = 1)
Definition at line 47 of file TEfficiency.h.
Parameter for prior beta distribution different bin by bin (default vector is empty)
Definition at line 48 of file TEfficiency.h.
! Pointer to a method calculating the boundaries of confidence intervals
Definition at line 50 of file TEfficiency.h.
|
protected |
Confidence level (default = 0.683, 1 sigma)
Definition at line 51 of file TEfficiency.h.
|
protected |
! Pointer to directory holding this TEfficiency object
Definition at line 52 of file TEfficiency.h.
|
protected |
->Pointer to list of functions
Definition at line 53 of file TEfficiency.h.
|
protected |
! Temporary graph for painting
Definition at line 54 of file TEfficiency.h.
|
protected |
! Temporary histogram for painting
Definition at line 55 of file TEfficiency.h.
|
protected |
Histogram for events which passed certain criteria.
Definition at line 56 of file TEfficiency.h.
|
protected |
Defines how the confidence intervals are determined.
Definition at line 57 of file TEfficiency.h.
|
protected |
Histogram for total number of events.
Definition at line 58 of file TEfficiency.h.
|
protected |
Weight for all events (default = 1)
Definition at line 59 of file TEfficiency.h.