TSpectrum3 Class Reference

Advanced 3-dimensional spectra processing functions.

Author

Miroslav Morhac

This class contains advanced spectra processing functions.

• Three-dimensional background estimation functions
• Three-dimensional smoothing functions
• Three-dimensional deconvolution functions
• Three-dimensional peak search functions

The algorithms in this class have been published in the following references:

[1] M.Morhac et al.: Background elimination methods for multidimensional coincidence gamma-ray spectra. Nuclear Instruments and Methods in Physics Research A 401 (1997) 113-132.

[2] M.Morhac et al.: Efficient one- and two-dimensional Gold deconvolution and its application to gamma-ray spectra decomposition. Nuclear Instruments and Methods in Physics Research A 401 (1997) 385-408.

[3] M. Morhac et al.: Efficient algorithm of multidimensional deconvolution and its application to nuclear data processing. Digital Signal Processing, Vol. 13, No. 1, (2003), 144-171.

[4] M.Morhac et al.: Identification of peaks in multidimensional coincidence gamma-ray spectra. Nuclear Instruments and Methods in Research Physics A 443(2000), 108-125.

These NIM papers are also available as Postscript files from:

• SpectrumDec.ps.gz
• SpectrumSrc.ps.gz
• SpectrumBck.ps.gz

See also the online documentation and tutorials.

Definition at line 18 of file TSpectrum3.h.

Public Types
enum	{ kBackIncreasingWindow =0 , kBackDecreasingWindow =1 , kBackSuccessiveFiltering =0 , kBackOneStepFiltering =1 }
Public Types inherited from TObject
enum	{   kIsOnHeap = 0x01000000 , kNotDeleted = 0x02000000 , kZombie = 0x04000000 , kInconsistent = 0x08000000 ,   kBitMask = 0x00ffffff }
enum	{ kSingleKey = BIT(0) , kOverwrite = BIT(1) , kWriteDelete = BIT(2) }
enum	EDeprecatedStatusBits { kObjInCanvas = BIT(3) }
enum	EStatusBits {   kCanDelete = BIT(0) , kMustCleanup = BIT(3) , kIsReferenced = BIT(4) , kHasUUID = BIT(5) ,   kCannotPick = BIT(6) , kNoContextMenu = BIT(8) , kInvalidObject = BIT(13) }

Public Member Functions
	TSpectrum3 ()
	Constructor.
	TSpectrum3 (Int_t maxpositions, Double_t resolution=1)
virtual	~TSpectrum3 ()
	Destructor.
virtual const char *	Background (const TH1 *hist, Int_t niter, Option_t *option="goff")
	This function calculates background spectrum from source in h.
const char *	Background (Double_t ***spectrum, Int_t ssizex, Int_t ssizey, Int_t ssizez, Int_t numberIterationsX, Int_t numberIterationsY, Int_t numberIterationsZ, Int_t direction, Int_t filterType)
	This function calculates background spectrum from source spectrum.
const char *	Deconvolution (Double_t ***source, const Double_t ***resp, Int_t ssizex, Int_t ssizey, Int_t ssizez, Int_t numberIterations, Int_t numberRepetitions, Double_t boost)
	This function calculates deconvolution from source spectrum according to response spectrum The result is placed in the cube pointed by source pointer.
TH1 *	GetHistogram () const
Int_t	GetNPeaks () const
Double_t *	GetPositionX () const
Double_t *	GetPositionY () const
Double_t *	GetPositionZ () const
virtual void	Print (Option_t *option="") const
	Print the array of positions.
virtual Int_t	Search (const TH1 *hist, Double_t sigma=2, Option_t *option="goff", Double_t threshold=0.05)
	This function searches for peaks in source spectrum in hin The number of found peaks and their positions are written into the members fNpeaks and fPositionX.
Int_t	SearchFast (const Double_t ***source, Double_t ***dest, Int_t ssizex, Int_t ssizey, Int_t ssizez, Double_t sigma, Double_t threshold, Bool_t markov, Int_t averWindow)
	THREE-DIMENSIONAL CLASSICAL PEAK SEARCH FUNCTION This function searches for peaks in source spectrum using the algorithm based on smoothed second differences.
Int_t	SearchHighRes (const Double_t ***source, Double_t ***dest, Int_t ssizex, Int_t ssizey, Int_t ssizez, Double_t sigma, Double_t threshold, Bool_t backgroundRemove, Int_t deconIterations, Bool_t markov, Int_t averWindow)
	This function searches for peaks in source spectrum It is based on deconvolution method.
void	SetResolution (Double_t resolution=1)
	NOT USED resolution: determines resolution of the neighbouring peaks default value is 1 correspond to 3 sigma distance between peaks.
const char *	SmoothMarkov (Double_t ***source, Int_t ssizex, Int_t ssizey, Int_t ssizez, Int_t averWindow)
	This function calculates smoothed spectrum from source spectrum based on Markov chain method.
Public Member Functions inherited from TNamed
	TNamed ()
	TNamed (const char *name, const char *title)
	TNamed (const TNamed &named)
	TNamed copy ctor.
	TNamed (const TString &name, const TString &title)
virtual	~TNamed ()
	TNamed destructor.
virtual void	Clear (Option_t *option="")
	Set name and title to empty strings ("").
virtual TObject *	Clone (const char *newname="") const
	Make a clone of an object using the Streamer facility.
virtual Int_t	Compare (const TObject *obj) const
	Compare two TNamed objects.
virtual void	Copy (TObject &named) const
	Copy this to obj.
virtual void	FillBuffer (char *&buffer)
	Encode TNamed into output buffer.
virtual const char *	GetName () const
	Returns name of object.
virtual const char *	GetTitle () const
	Returns title of object.
virtual ULong_t	Hash () const
	Return hash value for this object.
virtual Bool_t	IsSortable () const
virtual void	ls (Option_t *option="") const
	List TNamed name and title.
TNamed &	operator= (const TNamed &rhs)
	TNamed assignment operator.
virtual void	SetName (const char *name)
	Set the name of the TNamed.
virtual void	SetNameTitle (const char *name, const char *title)
	Set all the TNamed parameters (name and title).
virtual void	SetTitle (const char *title="")
	Set the title of the TNamed.
virtual Int_t	Sizeof () const
	Return size of the TNamed part of the TObject.
Public Member Functions inherited from TObject
	TObject ()
	TObject constructor.
	TObject (const TObject &object)
	TObject copy ctor.
virtual	~TObject ()
	TObject destructor.
void	AbstractMethod (const char *method) const
	Use this method to implement an "abstract" method that you don't want to leave purely abstract.
virtual void	AppendPad (Option_t *option="")
	Append graphics object to current pad.
virtual void	Browse (TBrowser *b)
	Browse object. May be overridden for another default action.
ULong_t	CheckedHash ()
	Check and record whether this class has a consistent Hash/RecursiveRemove setup (*) and then return the regular Hash value for this object.
virtual const char *	ClassName () const
	Returns name of class to which the object belongs.
virtual void	Delete (Option_t *option="")
	Delete this object.
virtual Int_t	DistancetoPrimitive (Int_t px, Int_t py)
	Computes distance from point (px,py) to the object.
virtual void	Draw (Option_t *option="")
	Default Draw method for all objects.
virtual void	DrawClass () const
	Draw class inheritance tree of the class to which this object belongs.
virtual TObject *	DrawClone (Option_t *option="") const
	Draw a clone of this object in the current selected pad for instance with: gROOT->SetSelectedPad(gPad).
virtual void	Dump () const
	Dump contents of object on stdout.
virtual void	Error (const char *method, const char *msgfmt,...) const
	Issue error message.
virtual void	Execute (const char *method, const char *params, Int_t *error=0)
	Execute method on this object with the given parameter string, e.g.
virtual void	Execute (TMethod *method, TObjArray *params, Int_t *error=0)
	Execute method on this object with parameters stored in the TObjArray.
virtual void	ExecuteEvent (Int_t event, Int_t px, Int_t py)
	Execute action corresponding to an event at (px,py).
virtual void	Fatal (const char *method, const char *msgfmt,...) const
	Issue fatal error message.
virtual TObject *	FindObject (const char *name) const
	Must be redefined in derived classes.
virtual TObject *	FindObject (const TObject *obj) const
	Must be redefined in derived classes.
virtual Option_t *	GetDrawOption () const
	Get option used by the graphics system to draw this object.
virtual const char *	GetIconName () const
	Returns mime type name of object.
virtual char *	GetObjectInfo (Int_t px, Int_t py) const
	Returns string containing info about the object at position (px,py).
virtual Option_t *	GetOption () const
virtual UInt_t	GetUniqueID () const
	Return the unique object id.
virtual Bool_t	HandleTimer (TTimer *timer)
	Execute action in response of a timer timing out.
Bool_t	HasInconsistentHash () const
	Return true is the type of this object is known to have an inconsistent setup for Hash and RecursiveRemove (i.e.
virtual void	Info (const char *method, const char *msgfmt,...) const
	Issue info message.
virtual Bool_t	InheritsFrom (const char *classname) const
	Returns kTRUE if object inherits from class "classname".
virtual Bool_t	InheritsFrom (const TClass *cl) const
	Returns kTRUE if object inherits from TClass cl.
virtual void	Inspect () const
	Dump contents of this object in a graphics canvas.
void	InvertBit (UInt_t f)
virtual Bool_t	IsEqual (const TObject *obj) const
	Default equal comparison (objects are equal if they have the same address in memory).
virtual Bool_t	IsFolder () const
	Returns kTRUE in case object contains browsable objects (like containers or lists of other objects).
R__ALWAYS_INLINE Bool_t	IsOnHeap () const
R__ALWAYS_INLINE Bool_t	IsZombie () const
void	MayNotUse (const char *method) const
	Use this method to signal that a method (defined in a base class) may not be called in a derived class (in principle against good design since a child class should not provide less functionality than its parent, however, sometimes it is necessary).
virtual Bool_t	Notify ()
	This method must be overridden to handle object notification.
void	Obsolete (const char *method, const char *asOfVers, const char *removedFromVers) const
	Use this method to declare a method obsolete.
void	operator delete (void *ptr)
	Operator delete.
void	operator delete[] (void *ptr)
	Operator delete [].
void *	operator new (size_t sz)
void *	operator new (size_t sz, void *vp)
void *	operator new[] (size_t sz)
void *	operator new[] (size_t sz, void *vp)
TObject &	operator= (const TObject &rhs)
	TObject assignment operator.
virtual void	Paint (Option_t *option="")
	This method must be overridden if a class wants to paint itself.
virtual void	Pop ()
	Pop on object drawn in a pad to the top of the display list.
virtual Int_t	Read (const char *name)
	Read contents of object with specified name from the current directory.
virtual void	RecursiveRemove (TObject *obj)
	Recursively remove this object from a list.
void	ResetBit (UInt_t f)
virtual void	SaveAs (const char *filename="", Option_t *option="") const
	Save this object in the file specified by filename.
virtual void	SavePrimitive (std::ostream &out, Option_t *option="")
	Save a primitive as a C++ statement(s) on output stream "out".
void	SetBit (UInt_t f)
void	SetBit (UInt_t f, Bool_t set)
	Set or unset the user status bits as specified in f.
virtual void	SetDrawOption (Option_t *option="")
	Set drawing option for object.
virtual void	SetUniqueID (UInt_t uid)
	Set the unique object id.
virtual void	SysError (const char *method, const char *msgfmt,...) const
	Issue system error message.
R__ALWAYS_INLINE Bool_t	TestBit (UInt_t f) const
Int_t	TestBits (UInt_t f) const
virtual void	UseCurrentStyle ()
	Set current style settings in this object This function is called when either TCanvas::UseCurrentStyle or TROOT::ForceStyle have been invoked.
virtual void	Warning (const char *method, const char *msgfmt,...) const
	Issue warning message.
virtual Int_t	Write (const char *name=0, Int_t option=0, Int_t bufsize=0)
	Write this object to the current directory.
virtual Int_t	Write (const char *name=0, Int_t option=0, Int_t bufsize=0) const
	Write this object to the current directory.

Protected Attributes
TH1 *	fHistogram
	resulting histogram
Int_t	fMaxPeaks
	Maximum number of peaks to be found.
Int_t	fNPeaks
	number of peaks found
Double_t *	fPosition
	[fNPeaks] array of current peak positions
Double_t *	fPositionX
	[fNPeaks] X positions of peaks
Double_t *	fPositionY
	[fNPeaks] Y positions of peaks
Double_t *	fPositionZ
	[fNPeaks] Z positions of peaks
Double_t	fResolution
	NOT USED resolution of the neighboring peaks
Protected Attributes inherited from TNamed
TString	fName
TString	fTitle

Additional Inherited Members
Static Public Member Functions inherited from TObject
static Long_t	GetDtorOnly ()
	Return destructor only flag.
static Bool_t	GetObjectStat ()
	Get status of object stat flag.
static void	SetDtorOnly (void *obj)
	Set destructor only flag.
static void	SetObjectStat (Bool_t stat)
	Turn on/off tracking of objects in the TObjectTable.
Protected Types inherited from TObject
enum	{ kOnlyPrepStep = BIT(3) }
Protected Member Functions inherited from TObject
virtual void	DoError (int level, const char *location, const char *fmt, va_list va) const
	Interface to ErrorHandler (protected).
void	MakeZombie ()

#include <TSpectrum3.h>

Inheritance diagram for TSpectrum3:

Member Enumeration Documentation

anonymous enum

anonymous enum

Enumerator
kBackIncreasingWindow
kBackDecreasingWindow
kBackSuccessiveFiltering
kBackOneStepFiltering

Definition at line 30 of file TSpectrum3.h.

Constructor & Destructor Documentation

TSpectrum3() [1/2]

TSpectrum3::TSpectrum3

(

)

Constructor.

Definition at line 58 of file TSpectrum3.cxx.

TSpectrum3() [2/2]

TSpectrum3::TSpectrum3	(	Int_t	maxpositions,
		Double_t	resolution = 1
	)

• maxpositions: maximum number of peaks
• resolution: NOT USED determines resolution of the neighbouring peaks default value is 1 correspond to 3 sigma distance between peaks. Higher values allow higher resolution (smaller distance between peaks. May be set later through SetResolution.

Definition at line 80 of file TSpectrum3.cxx.

~TSpectrum3()

TSpectrum3::~TSpectrum3 ( )

virtual

Destructor.

Definition at line 97 of file TSpectrum3.cxx.

Member Function Documentation

Background() [1/2]

const char * TSpectrum3::Background ( const TH1 *  h, Int_t  number_of_iterations, Option_t *  option = "goff"  )

virtual

This function calculates background spectrum from source in h.

The result is placed in the vector pointed by spectrum pointer.

Function parameters:

• spectrum: pointer to the vector of source spectrum
• size: length of spectrum and working space vectors
• number_of_iterations, for details we refer to manual

Definition at line 115 of file TSpectrum3.cxx.

Background() [2/2]

const char * TSpectrum3::Background	(	Double_t ***	spectrum,
		Int_t	ssizex,
		Int_t	ssizey,
		Int_t	ssizez,
		Int_t	numberIterationsX,
		Int_t	numberIterationsY,
		Int_t	numberIterationsZ,
		Int_t	direction,
		Int_t	filterType
	)

This function calculates background spectrum from source spectrum.

The result is placed to the array pointed by spectrum pointer.

Function parameters:

• spectrum-pointer to the array of source spectrum
• ssizex-x length of spectrum
• ssizey-y length of spectrum
• ssizez-z length of spectrum
• numberIterationsX-maximal x width of clipping window
• numberIterationsY-maximal y width of clipping window
• numberIterationsZ-maximal z width of clipping window for details we refer to manual
• direction- direction of change of clipping window
  • possible values=kBackIncreasingWindow, kBackDecreasingWindow
• filterType-determines the algorithm of the filtering -possible values=kBackSuccessiveFiltering, kBackOneStepFiltering

Background estimation

Goal: Separation of useful information (peaks) from useless information (background)

• method is based on Sensitive Nonlinear Iterative Peak (SNIP) clipping algorithm [1]
• there exist two algorithms for the estimation of new value in the channel \(i_1, i_2, i_3\)

Algorithm based on Successive Comparisons

It is an extension of one-dimensional SNIP algorithm to another dimension. For details we refer to [2].

Algorithm based on One Step Filtering

The algorithm is analogous to that for 2-dimensional data. For details we refer to TSpectrum2. New value in the estimated channel is calculated as \( a = \nu_{p-1}(i_1, i_2, i_3)\)

\[ \nu_p(i_1, i_2, i_3) = min (a,b) \]

where p = 1, 2, ..., number_of_iterations.

References:

[1] C. G Ryan et al.: SNIP, a statistics-sensitive background treatment for the quantitative analysis of PIXE spectra in geoscience applications. NIM, B34 (1988), 396-402./

[2] M.Morhac, J. Kliman, V. Matouoek, M. Veselsky, I. Turzo.: Background elimination methods for multidimensional gamma-ray spectra. NIM, A401 (1997) 113-132.

Example 1- script Back3.c :

Fig. 1 Original three-dimensional gamma-gamma-gamma-ray spectrum

Fig. 2 Background estimated from data from Fig. 1 using decreasing clipping window with widths 5, 5, 5 and algorithm based on successive comparisons. The estimate includes not only continuously changing background but also one- and two-dimensional ridges.

Fig. 3 Resulting peaks after subtraction of the estimated background (Fig. 2) from original three-dimensional gamma-gamma-gamma-ray spectrum (Fig. 1).

Script:

Example to illustrate the background estimator (class TSpectrum3). To execute this example, do:

root > .x Back3.C

  void Back3() {
     Int_t i, j, k;
     Int_t nbinsx = 64;
     Int_t nbinsy = 64;
     Int_t nbinsz = 64;
     Int_t xmin = 0;
     Int_t xmax = nbinsx;
     Int_t ymin = 0;
     Int_t ymax = nbinsy;
     Int_t zmin = 0;
     Int_t zmax = nbinsz;
     Double_t*** source = new Double_t**[nbinsx];
     Double_t*** dest = new Double_t**[nbinsx];
     for(i=0;i<nbinsx;i++){
        source[i]=new Double_t*[nbinsy];
        for(j=0;j<nbinsy;j++)
           source[i][j]=new Double_t[nbinsz];
     }
     for(i=0;i<nbinsx;i++){
        dest[i]=new Double_t*[nbinsy];
        for(j=0;j<nbinsy;j++)
           dest[i][j]=new Double_t[nbinsz];
     }
     TH3F *back = new TH3F("back","Background estimation",nbinsx,xmin,xmax,nbinsy,ymin,ymax,nbinsz,zmin,zmax);
     TFile *f = new TFile("TSpectrum3.root");
     back=(TH3F*)f->Get("back;1");
     TCanvas *Background = new TCanvas("Background","Estimation of background with decreasing window",10,10,1000,700);
     TSpectrum3 *s = new TSpectrum3();
     for (i = 0; i < nbinsx; i++){
        for (j = 0; j < nbinsy; j++){
              for (k = 0; k < nbinsz; k++){
                 source[i][j][k] = back->GetBinContent(i + 1,j + 1,k + 1);
                 dest[i][j][k] = back->GetBinContent(i + 1,j + 1,k + 1);
              }
        }
     }
     s->Background(dest,nbinsx,nbinsy,nbinsz,5,5,5,s->kBackDecreasingWindow,s->kBackSuccessiveFiltering);
     for (i = 0; i < nbinsx; i++){
        for (j = 0; j < nbinsy; j++){
           for (k = 0; k < nbinsz; k++){
              back->SetBinContent(i + 1,j + 1,k + 1, dest[i][j][k]);
           }
        }
     }
     FILE *out;
     char PATH[80];
     strcpy(PATH,"spectra3/back_output_5ds.spe");
     out=fopen(PATH,"wb");
     for(i=0;i<nbinsx;i++){
        for(j=0;j<nbinsy;j++){
           fwrite(dest[i][j], sizeof(dest[0][0][0]),nbinsz,out);
        }
     }
     fclose(out);
     for (i = 0; i < nbinsx; i++){
        for (j = 0; j <nbinsy; j++){
           for (k = 0; k <nbinsz; k++){
              source[i][j][k] = source[i][j][k] - dest[i][j][k];
           }
        }
     }
     for (i = 0; i < nbinsx; i++){
        for (j = 0; j < nbinsy; j++){
           for (k = 0; k < nbinsz; k++){
              back->SetBinContent(i + 1,j + 1,k + 1, source[i][j][k]);
           }
        }
     }
     strcpy(PATH,"spectra3/back_peaks_5ds.spe");
     out=fopen(PATH,"wb");
     for(i=0;i<nbinsx;i++){
        for(j=0;j<nbinsy;j++){
           fwrite(source[i][j], sizeof(source[0][0][0]),nbinsz,out);
        }
     }
     fclose(out);
     back->Draw("");
}

Definition at line 384 of file TSpectrum3.cxx.

Deconvolution()

const char * TSpectrum3::Deconvolution	(	Double_t ***	source,
		const Double_t ***	resp,
		Int_t	ssizex,
		Int_t	ssizey,
		Int_t	ssizez,
		Int_t	numberIterations,
		Int_t	numberRepetitions,
		Double_t	boost
	)

This function calculates deconvolution from source spectrum according to response spectrum The result is placed in the cube pointed by source pointer.

Function parameters:

• source-pointer to the cube of source spectrum
• resp-pointer to the cube of response spectrum
• ssizex-x length of source and response spectra
• ssizey-y length of source and response spectra
• ssizey-y length of source and response spectra
• numberIterations, for details we refer to manual
• numberRepetitions, for details we refer to manual
• boost, boosting factor, for details we refer to manual

Deconvolution

Goal: Improvement of the resolution in spectra, decomposition of multiplets

Mathematical formulation of the 3-dimensional convolution system is

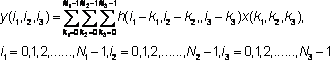
where h(i,j,k) is the impulse response function, x, y are input and output fields, respectively, \( N_1, N_2, N3\), are the lengths of x and h fields

• let us assume that we know the response and the output fields (spectra) of the above given system.
• the deconvolution represents solution of the overdetermined system of linear equations, i.e., the calculation of the field -x.
• from numerical stability point of view the operation of deconvolution is extremely critical (ill-posed problem) as well as time consuming operation.
• the Gold deconvolution algorithm proves to work very well even for 2-dimensional systems. Generalization of the algorithm for 2-dimensional systems was presented in [1], and for multidimensional systems in [2].
• for Gold deconvolution algorithm as well as for boosted deconvolution algorithm we refer also to TSpectrum and TSpectrum2

References:

[1] M.Morhac, J. Kliman, V. Matouoek, M. Veselsky, I. Turzo.: Efficient one- and two-dimensional Gold deconvolution and its application to gamma-ray spectra decomposition. NIM, A401 (1997) 385-408.

[2] Morhac M., Matouoek V., Kliman J., Efficient algorithm of multidimensional deconvolution and its application to nuclear data processing, Digital Signal Processing 13 (2003) 144.

Example 1 - script Decon.c :

response function (usually peak) should be shifted to the beginning of the coordinate system (see Fig. 1)

Fig. 1 Three-dimensional response spectrum

Fig. 2 Three-dimensional input spectrum (before deconvolution)

Fig. 3 Spectrum from Fig. 2 after deconvolution (100 iterations)

Script:

Example to illustrate the Gold deconvolution (class TSpectrum3). To execute this example, do:

root > .x Decon3.C

#include <TSpectrum3>
void Decon3() {
   Int_t i, j, k;
   Int_t nbinsx = 32;
   Int_t nbinsy = 32;
   Int_t nbinsz = 32;
   Int_t xmin = 0;
   Int_t xmax = nbinsx;
   Int_t ymin = 0;
   Int_t ymax = nbinsy;
   Int_t zmin = 0;
   Int_t zmax = nbinsz;
   Double_t*** source = newDouble_t**[nbinsx];
   Double_t*** resp = new Double_t**[nbinsx];
   for(i=0;i<nbinsx;i++){
      source[i]=new Double_t* [nbinsy];
      for(j=0;j<nbinsy;j++)
         source[i][j]=new Double_t[nbinsz];
   }
   for(i=0;i<nbinsx;i++){
      resp[i]=new Double_t*[nbinsy];
      for(j=0;j<nbinsy;j++)
         resp[i][j]=new Double_t[nbinsz];
   }
   TH3F *decon_in = new TH3F("decon_in","Deconvolution",nbinsx,xmin,xmax,nbinsy,ymin,ymax,nbinsz,zmin,zmax);
   TH3F *decon_resp = new TH3F("decon_resp","Deconvolution",nbinsx,xmin,xmax,nbinsy,ymin,ymax,nbinsz,zmin,zmax);
   TFile *f = new TFile("TSpectrum3.root");
   decon_in=(TH3F*) f->Get("decon_in;1");
   decon_resp=(TH3F*) f->Get("decon_resp;1");
   TCanvas *Deconvolution = new TCanvas("Deconvolution","Deconvolution of 3-dimensional spectra",10,10,1000,700);
   TSpectrum3 *s = new TSpectrum3();
   for (i = 0; i < nbinsx; i++){
      for (j = 0; j < nbinsy; j++){
            for (k = 0; k < nbinsz; k++){
               source[i][j][k] = decon_in->GetBinContent(i + 1,j + 1,k + 1);
               resp[i][j][k] = decon_resp->GetBinContent(i + 1,j + 1,k + 1);
            }
      }
   }
   s->Deconvolution(source,resp,nbinsx,nbinsy,nbinsz,100,1,1);
   for (i = 0; i < nbinsx; i++){
      for (j = 0; j < nbinsy; j++){
         for (k = 0; k < nbinsz; k++){
            decon_in->SetBinContent(i + 1,j + 1,k + 1, source[i][j][k]);
         }
      }
   }
   decon_in->Draw("");
}

Example 2 - script Decon_hr.c :

This example illustrates repeated Gold deconvolution with boosting. After every 10 iterations we apply power function with exponent = 2 to the spectrum given in Fig. 2.

Fig. 4 Spectrum from Fig. 2 after boosted deconvolution (10 iterations repeated 10 times). It decomposes completely cluster of peaks from Fig 2.

Script:

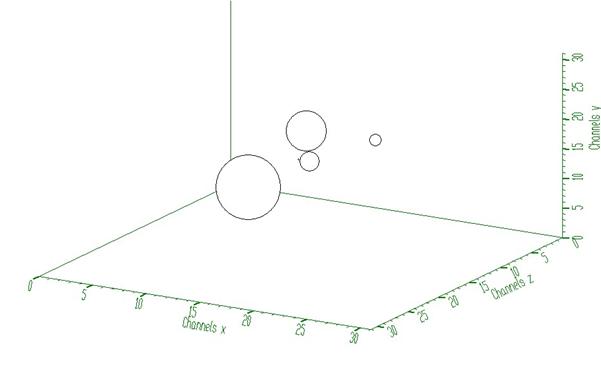
Example to illustrate the Gold deconvolution (class TSpectrum3). To execute this example, do:

root > .x Decon3_hr.C

void Decon3_hr() {
   Int_t i, j, k;
   Int_t nbinsx = 32;
   Int_t nbinsy = 32;
   Int_t nbinsz = 32;
   Int_t xmin = 0;
   Int_t xmax = nbinsx;
   Int_t ymin = 0;
   Int_t ymax = nbinsy;
   Int_t zmin = 0;
   Int_t zmax = nbinsz;
   Double_t*** source = new Double_t**[nbinsx];
   Double_t*** resp = new Double_t**[nbinsx];
   for(i=0;i<nbinsx;i++){
      source[i]=new Double_t*[nbinsy];
      for(j=0;j<nbinsy;j++)
         source[i][j]=new Double_t[nbinsz];
   }
   for(i=0;i<nbinsx;i++){
      resp[i]=new Double_t*[nbinsy];
      for(j=0;j<nbinsy;j++)
         resp[i][j]=new Double_t[nbinsz];
   }
   TH3F *decon_in = new TH3F("decon_in","Deconvolution",nbinsx,xmin,xmax,nbinsy,ymin,ymax,nbinsz,zmin,zmax);
   TH3F *decon_resp = new TH3F("decon_resp","Deconvolution",nbinsx,xmin,xmax,nbinsy,ymin,ymax,nbinsz,zmin,zmax);
   TFile *f = new TFile("TSpectrum3.root");
   decon_in=(TH3F*)f->Get("decon_in;1");
   decon_resp=(TH3F*)f->Get("decon_resp;1");
   TCanvas *Deconvolution = new TCanvas("Deconvolution","High resolution deconvolution of 3-dimensional spectra",10,10,1000,700);
   TSpectrum3 *s = new TSpectrum3();
   for (i = 0; i < nbinsx; i++){
      for (j = 0; j < nbinsy; j++){
         for (k = 0; k < nbinsz; k++){
            source[i][j][k] = decon_in->GetBinContent(i + 1,j + 1,k + 1);
            resp[i][j][k] = decon_resp->GetBinContent(i + 1,j + 1,k + 1);
         }
      }
   }
   s->Deconvolution(source,resp,nbinsx,nbinsy,nbinsz,10,10,2);
   for (i = 0; i < nbinsx; i++){
      for (j = 0; j < nbinsy; j++){
         for (k = 0; k < nbinsz; k++){
            decon_in->SetBinContent(i + 1,j + 1,k + 1, source[i][j][k]);
         }
      }
   }
   decon_in->Draw("");
}

Definition at line 1597 of file TSpectrum3.cxx.

GetHistogram()

TH1 * TSpectrum3::GetHistogram ( ) const

inline

Definition at line 43 of file TSpectrum3.h.

GetNPeaks()

Int_t TSpectrum3::GetNPeaks ( ) const

inline

Definition at line 44 of file TSpectrum3.h.

GetPositionX()

Double_t * TSpectrum3::GetPositionX ( ) const

inline

Definition at line 45 of file TSpectrum3.h.

GetPositionY()

Double_t * TSpectrum3::GetPositionY ( ) const

inline

Definition at line 46 of file TSpectrum3.h.

GetPositionZ()

Double_t * TSpectrum3::GetPositionZ ( ) const

inline

Definition at line 47 of file TSpectrum3.h.

Print()

void TSpectrum3::Print ( Option_t *  option = "" ) const

virtual

Print the array of positions.

Reimplemented from TNamed.

Definition at line 126 of file TSpectrum3.cxx.

Search()

Int_t TSpectrum3::Search ( const TH1 *  hin, Double_t  sigma = 2, Option_t *  option = "goff", Double_t  threshold = 0.05  )

virtual

This function searches for peaks in source spectrum in hin The number of found peaks and their positions are written into the members fNpeaks and fPositionX.

Function parameters:

• hin: pointer to the histogram of source spectrum
• sigma: sigma of searched peaks, for details we refer to manual Note that sigma is in number of bins

• threshold: (default=0.05) peaks with amplitude less than threshold*highest_peak are discarded.

  if option is not equal to "goff" (goff is the default), then a polymarker object is created and added to the list of functions of the histogram. The histogram is drawn with the specified option and the polymarker object drawn on top of the histogram. The polymarker coordinates correspond to the npeaks peaks found in the histogram. A pointer to the polymarker object can be retrieved later via:

  TList *functions = hin->GetListOfFunctions();
  TPolyMarker *pm = (TPolyMarker*)functions->FindObject("TPolyMarker")

Definition at line 160 of file TSpectrum3.cxx.

SearchFast()

Int_t TSpectrum3::SearchFast	(	const Double_t ***	source,
		Double_t ***	dest,
		Int_t	ssizex,
		Int_t	ssizey,
		Int_t	ssizez,
		Double_t	sigma,
		Double_t	threshold,
		Bool_t	markov,
		Int_t	averWindow
	)

THREE-DIMENSIONAL CLASSICAL PEAK SEARCH FUNCTION This function searches for peaks in source spectrum using the algorithm based on smoothed second differences.

Function parameters:

• source-pointer to the matrix of source spectrum
• ssizex-x length of source spectrum
• ssizey-y length of source spectrum
• ssizez-z length of source spectrum
• sigma-sigma of searched peaks, for details we refer to manual
• threshold-threshold value in % for selected peaks, peaks with amplitude less than threshold*highest_peak/100 are ignored, see manual
• markov-logical variable, if it is true, first the source spectrum is replaced by new spectrum calculated using Markov chains method.
• averWindow-averaging window of searched peaks, for details we refer to manual (applies only for Markov method)

Definition at line 3174 of file TSpectrum3.cxx.

SearchHighRes()

Int_t TSpectrum3::SearchHighRes	(	const Double_t ***	source,
		Double_t ***	dest,
		Int_t	ssizex,
		Int_t	ssizey,
		Int_t	ssizez,
		Double_t	sigma,
		Double_t	threshold,
		Bool_t	backgroundRemove,
		Int_t	deconIterations,
		Bool_t	markov,
		Int_t	averWindow
	)

This function searches for peaks in source spectrum It is based on deconvolution method.

First the background is removed (if desired), then Markov spectrum is calculated (if desired), then the response function is generated according to given sigma and deconvolution is carried out. It returns number of found peaks.

Function parameters:

• source-pointer to the matrix of source spectrum
• dest-pointer to the matrix of resulting deconvolved spectrum
• ssizex-x length of source spectrum
• ssizey-y length of source spectrum
• ssizez-z length of source spectrum
• sigma-sigma of searched peaks, for details we refer to manual
• threshold-threshold value in % for selected peaks, peaks with amplitude less than threshold*highest_peak/100 are ignored, see manual
• backgroundRemove-logical variable, set if the removal of background before deconvolution is desired
• deconIterations-number of iterations in deconvolution operation
• markov-logical variable, if it is true, first the source spectrum is replaced by new spectrum calculated using Markov chains method.
• averWindow-averaging window of searched peaks, for details we refer to manual (applies only for Markov method)

Peaks searching

Goal: to identify automatically the peaks in spectrum with the presence of the continuous background, one- and two-fold coincidences (ridges) and statistical fluctuations - noise.

The common problems connected with correct peak identification in three-dimensional coincidence spectra are

• non-sensitivity to noise, i.e., only statistically relevant peaks should be identified
• non-sensitivity of the algorithm to continuous background
• non-sensitivity to one-fold coincidences (coincidences peak - peak - background in all dimensions) and their crossings
• non-sensitivity to two-fold coincidences (coincidences peak - background - background in all dimensions) and their crossings
• ability to identify peaks close to the edges of the spectrum region
• resolution, decomposition of doublets and multiplets. The algorithm should be able to recognise close positioned peaks.

References:

[1] M.A. Mariscotti: A method for identification of peaks in the presence of background and its application to spectrum analysis. NIM 50 (1967), 309-320.

[2] M.Morhac, J. Kliman, V. Matouoek, M. Veselsky, I. Turzo.:Identification of peaks in multidimensional coincidence gamma-ray spectra. NIM, A443 (2000) 108-125.

[3] Z.K. Silagadze, A new algorithm for automatic photo-peak searches. NIM A 376 (1996), 451.

Example of peak searching method

SearchHighRes function provides users with the possibility to vary the input parameters and with the access to the output deconvolved data in the destination spectrum. Based on the output data one can tune the parameters.

Example 1 - script Search3.c:

Fig. 1 Three-dimensional spectrum with 5 peaks (sigma=2, threshold=5%, 3 iterations steps in the deconvolution)

Fig. 2 Spectrum from Fig. 1 after background elimination and deconvolution

Script:

Example to illustrate high resolution peak searching function (class TSpectrum3). To execute this example, do:

root > .x Search3.C

void Search3() {
   Int_t i, j, k, nfound;
   Int_t nbinsx = 32;
   Int_t nbinsy = 32;
   Int_t nbinsz = 32;
   Int_t xmin = 0;
   Int_t xmax = nbinsx;
   Int_t ymin = 0;
   Int_t ymax = nbinsy;
   Int_t zmin = 0;
   Int_t zmax = nbinsz;
   Double_t*** source = new Double_t**[nbinsx];
   Double_t*** dest = new Double_t**[nbinsx];
   for(i=0;i<nbinsx;i++){
      source[i]=new Double_t*[nbinsy];
      for(j=0;j<nbinsy;j++)
         source[i][j]=new Double_t[nbinsz];
    }
   for(i=0;i<nbinsx;i++){
      dest[i]=new Double_t*[nbinsy];
      for(j=0;j<nbinsy;j++)
         dest[i][j]=new Double_t [nbinsz];
   }
   TH3F *search = new TH3F("Search","Peak searching",nbinsx,xmin,xmax,nbinsy,ymin,ymax,nbinsz,zmin,zmax);
   TFile *f = new TFile("TSpectrum3.root");
   search=(TH3F*)f->Get("search2;1");
   TCanvas *Search = new TCanvas("Search","Peak searching",10,10,1000,700);
   TSpectrum3 *s = new TSpectrum3();
   for (i = 0; i < nbinsx; i++){
      for (j = 0; j < nbinsy; j++){
         for (k = 0; k < nbinsz; k++){
            source[i][j][k] = search->GetBinContent(i + 1,j + 1,k + 1);
         }
      }
   }
   nfound = s->SearchHighRes(source, dest, nbinsx, nbinsy, nbinsz, 2, 5, kTRUE, 3, kFALSE, 3);
   printf("Found %d candidate peaks\n",nfound);
   for (i = 0; i < nbinsx; i++){
      for (j = 0; j < nbinsy; j++){
         for (k = 0; k < nbinsz; k++){
            search->SetBinContent(i + 1,j + 1,k + 1, dest[i][j][k]);
         }
      }
   }
   Double_t *PosX = new Double_t[nfound];
   Double_t *PosY = new Double_t[nfound];
   Double_t *PosZ = new Double_t[nfound];
   PosX = s->GetPositionX();
   PosY = s->GetPositionY();
   PosZ = s->GetPositionZ();
   for(i=0;i<nfound;i++)
         printf("posx= %d, posy= %d, posz=%d\n",(Int_t)(PosX[i]+0.5), (Int_t)(PosY[i]+0.5),(Int_t)(PosZ[i]+0.5));
   search->Draw("");
}

Definition at line 1946 of file TSpectrum3.cxx.

SetResolution()

void TSpectrum3::SetResolution

(

Double_t

resolution = 1

)

NOT USED resolution: determines resolution of the neighbouring peaks default value is 1 correspond to 3 sigma distance between peaks.

Higher values allow higher resolution (smaller distance between peaks. May be set later through SetResolution.

Definition at line 227 of file TSpectrum3.cxx.

SmoothMarkov()

const char * TSpectrum3::SmoothMarkov	(	Double_t ***	source,
		Int_t	ssizex,
		Int_t	ssizey,
		Int_t	ssizez,
		Int_t	averWindow
	)

This function calculates smoothed spectrum from source spectrum based on Markov chain method.

The result is placed in the array pointed by spectrum pointer.

Function parameters:

• source-pointer to the array of source spectrum
• working_space-pointer to the working array
• ssizex-x length of spectrum and working space arrays
• ssizey-y length of spectrum and working space arrays
• ssizey-z length of spectrum and working space arrays
• averWindow-width of averaging smoothing window

Smoothing

Goal: Suppression of statistical fluctuations the algorithm is based on discrete Markov chain, which has very simple invariant distribution

\[ U_2 = \frac{p_{1.2}}{p_{2,1}}U_1, U_3 = \frac{p_{2,3}}{p_{3,2}}U_2 U_1, ... , U_n = \frac{p_{n-1,n}}{p_{n,n-1}}U_{n-1} ... U_2 U_1 \]

\(U_1\) being defined from the normalization condition \( \sum_{i=1}^{n} U_i = 1\) n is the length of the smoothed spectrum and

\[ p_{i,i\pm1} = A_i \sum_{k=1}^{m} exp\left[\frac{y(i\pm k)-y(i)}{y(i\pm k)+y(i)}\right] \]

is the probability of the change of the peak position from channel i to the channel i+1. \(A_i\) is the normalization constant so that \( p_{i,i-1}+p_{i,i+1}=1\) and m is a width of smoothing window. We have extended this algorithm to three dimensions.

Reference:

[1] Z.K. Silagadze, A new algorithm for automatic photo-peak searches. NIM A 376 (1996), 451-.

Example 1 - script SmootMarkov3.c :

Fig. 1 Original noisy spectrum.

Fig. 2 Smoothed spectrum with averaging window m=3.

Script:

Example to illustrate the Markov smoothing (class TSpectrum3). To execute this example, do:

root > .x SmoothMarkov3.C

void SmoothMarkov3() {
   Int_t i, j, k;
   Int_t nbinsx = 64;
   Int_t nbinsy = 64;
   Int_t nbinsz = 64;
   Int_t xmin = 0;
   Int_t xmax = nbinsx;
   Int_t ymin = 0;
   Int_t ymax = nbinsy;
   Int_t zmin = 0;
   Int_t zmax = nbinsz;
   Double_t*** source = new Double_t**[nbinsx];
   for(i=0;i<nbinsx;i++){
      source[i]=new Double_t*[nbinsy];
      for(j=0;j<nbinsy;j++)
         source[i][j]=new Double_t[nbinsz];
   }
   TH3F *sm = new TH3F("Smoothing","Markov smoothing",nbinsx,xmin,xmax,nbinsy,ymin,ymax,nbinsz,zmin,zmax);
   TFile *f = new TFile("TSpectrum3.root");
   sm=(TH3F*)f->Get("back;1");
   TCanvas *Background = new TCanvas("Smoothing","Markov smoothing",10,10,1000,700);
   TSpectrum3 *s = new TSpectrum3();
   for (i = 0; i < nbinsx; i++){
      for (j = 0; j < nbinsy; j++){
            for (k = 0; k < nbinsz; k++){
               source[i][j][k] = sm->GetBinContent(i + 1,j + 1,k + 1);
            }
      }
   }
   s->SmoothMarkov(source,nbinsx,nbinsy,nbinsz,3);
   for (i = 0; i < nbinsx; i++){
      for (j = 0; j < nbinsy; j++){
         for (k = 0; k < nbinsz; k++){
            sm->SetBinContent(i + 1,j + 1,k + 1, source[i][j][k]);
         }
      }
   }
   sm->Draw("");
}

Definition at line 859 of file TSpectrum3.cxx.

Member Data Documentation

fHistogram

TH1* TSpectrum3::fHistogram

protected

resulting histogram

Definition at line 27 of file TSpectrum3.h.

fMaxPeaks

Int_t TSpectrum3::fMaxPeaks

protected

Maximum number of peaks to be found.

Definition at line 20 of file TSpectrum3.h.

fNPeaks

Int_t TSpectrum3::fNPeaks

protected

number of peaks found

Definition at line 21 of file TSpectrum3.h.

fPosition

Double_t* TSpectrum3::fPosition

protected

[fNPeaks] array of current peak positions

Definition at line 22 of file TSpectrum3.h.

fPositionX

Double_t* TSpectrum3::fPositionX

protected

[fNPeaks] X positions of peaks

Definition at line 23 of file TSpectrum3.h.

fPositionY

Double_t* TSpectrum3::fPositionY

protected

[fNPeaks] Y positions of peaks

Definition at line 24 of file TSpectrum3.h.

fPositionZ

Double_t* TSpectrum3::fPositionZ

protected

[fNPeaks] Z positions of peaks

Definition at line 25 of file TSpectrum3.h.

fResolution

Double_t TSpectrum3::fResolution

protected

NOT USED resolution of the neighboring peaks

Definition at line 26 of file TSpectrum3.h.

Libraries for TSpectrum3:

---

The documentation for this class was generated from the following files:

• hist/spectrum/inc/TSpectrum3.h
• hist/spectrum/src/TSpectrum3.cxx