TH1 Class Reference

TH1 is the base class of all histogram classes in ROOT.

It provides the common interface for operations such as binning, filling, drawing, which will be detailed below.

1. Creating histograms
   • Labelling axes
2. Binning
   • Fix or variable bin size
   • Convention for numbering bins
   • Alphanumeric Bin Labels
   • Histograms with automatic bins
   • Rebinning
3. Filling histograms
   • Associated errors
   • Associated functions
   • Projections of histograms
   • Random Numbers and histograms
   • Making a copy of an histogram
   • Normalizing histograms
4. Drawing histograms
   • Setting Drawing histogram contour levels (2-D hists only)
   • Setting histogram graphics attributes
   • Customising how axes are drawn
5. Saving/reading histograms to/from a ROOT file
6. Operations on histograms
   • Fitting histograms
7. Miscellaneous operations

ROOT supports the following histogram types:

• 1-D histograms:
  • TH1C : histograms with one byte per channel. Maximum bin content = 127
  • TH1S : histograms with one short per channel. Maximum bin content = 32767
  • TH1I : histograms with one int per channel. Maximum bin content = INT_MAX (*)
  • TH1F : histograms with one float per channel. Maximum precision 7 digits
  • TH1D : histograms with one double per channel. Maximum precision 14 digits
• 2-D histograms:
  • TH2C : histograms with one byte per channel. Maximum bin content = 127
  • TH2S : histograms with one short per channel. Maximum bin content = 32767
  • TH2I : histograms with one int per channel. Maximum bin content = INT_MAX (*)
  • TH2F : histograms with one float per channel. Maximum precision 7 digits
  • TH2D : histograms with one double per channel. Maximum precision 14 digits
• 3-D histograms:
  • TH3C : histograms with one byte per channel. Maximum bin content = 127
  • TH3S : histograms with one short per channel. Maximum bin content = 32767
  • TH3I : histograms with one int per channel. Maximum bin content = INT_MAX (*)
  • TH3F : histograms with one float per channel. Maximum precision 7 digits
  • TH3D : histograms with one double per channel. Maximum precision 14 digits
• Profile histograms: See classes TProfile, TProfile2D and TProfile3D. Profile histograms are used to display the mean value of Y and its standard deviation for each bin in X. Profile histograms are in many cases an elegant replacement of two-dimensional histograms : the inter-relation of two measured quantities X and Y can always be visualized by a two-dimensional histogram or scatter-plot; If Y is an unknown (but single-valued) approximate function of X, this function is displayed by a profile histogram with much better precision than by a scatter-plot.

^{(*) INT_MAX = 2147483647 is the maximum value for a variable of type int.}

The inheritance hierarchy looks as follows:

Creating histograms

Histograms are created by invoking one of the constructors, e.g.

TH1F *h1 = new TH1F("h1", "h1 title", 100, 0, 4.4);
TH2F *h2 = new TH2F("h2", "h2 title", 40, 0, 4, 30, -3, 3);

Histograms may also be created by:

• calling the Clone function, see below
• making a projection from a 2-D or 3-D histogram, see below
• reading an histogram from a file

When a histogram is created, a reference to it is automatically added to the list of in-memory objects for the current file or directory. This default behaviour can be changed by:

h->SetDirectory(0);          // for the current histogram h
TH1::AddDirectory(kFALSE);   // sets a global switch disabling the referencing

When the histogram is deleted, the reference to it is removed from the list of objects in memory. When a file is closed, all histograms in memory associated with this file are automatically deleted.

Labelling axes

Axis titles can be specified in the title argument of the constructor. They must be separated by ";":

TH1F* h=new TH1F("h", "Histogram title;X Axis;Y Axis", 100, 0, 1);

The histogram title and the axis titles can be any TLatex string, and are persisted if a histogram is written to a file.

Any title can be omitted:

TH1F* h=new TH1F("h", "Histogram title;;Y Axis", 100, 0, 1);
TH1F* h=new TH1F("h", ";;Y Axis", 100, 0, 1);

The method SetTitle() has the same syntax:

h->SetTitle("Histogram title;Another X title Axis");

Alternatively, the title of each axis can be set directly:

h->GetXaxis()->SetTitle("X axis title");
h->GetYaxis()->SetTitle("Y axis title");

For bin labels see binning.

Binning

Fix or variable bin size

All histogram types support either fix or variable bin sizes. 2-D histograms may have fix size bins along X and variable size bins along Y or vice-versa. The functions to fill, manipulate, draw or access histograms are identical in both cases.

Each histogram always contains 3 axis objects of type TAxis: fXaxis, fYaxis and fZaxis. To access the axis parameters, use:

TAxis *xaxis = h->GetXaxis(); etc.
Double_t binCenter = xaxis->GetBinCenter(bin), etc.

See class TAxis for a description of all the access functions. The axis range is always stored internally in double precision.

Convention for numbering bins

For all histogram types: nbins, xlow, xup

bin = 0;       underflow bin
bin = 1;       first bin with low-edge xlow INCLUDED
bin = nbins;   last bin with upper-edge xup EXCLUDED
bin = nbins+1; overflow bin

In case of 2-D or 3-D histograms, a "global bin" number is defined. For example, assuming a 3-D histogram with (binx, biny, binz), the function

Int_t gbin = h->GetBin(binx, biny, binz);

returns a global/linearized gbin number. This global gbin is useful to access the bin content/error information independently of the dimension. Note that to access the information other than bin content and errors one should use the TAxis object directly with e.g.:

Double_t xcenter = h3->GetZaxis()->GetBinCenter(27);

returns the center along z of bin number 27 (not the global bin) in the 3-D histogram h3.

Alphanumeric Bin Labels

By default, an histogram axis is drawn with its numeric bin labels. One can specify alphanumeric labels instead with:

• call TAxis::SetBinLabel(bin, label); This can always be done before or after filling. When the histogram is drawn, bin labels will be automatically drawn. See examples labels1.C and labels2.C
• call to a Fill function with one of the arguments being a string, e.g.

  hist1->Fill(somename, weight);
  hist2->Fill(x, somename, weight);
  hist2->Fill(somename, y, weight);
  hist2->Fill(somenamex, somenamey, weight);

  See examples hlabels1.C and hlabels2.C
• via TTree::Draw. see for example cernstaff.C

  tree.Draw("Nation::Division");

  where "Nation" and "Division" are two branches of a Tree.

When using the options 2 or 3 above, the labels are automatically added to the list (THashList) of labels for a given axis. By default, an axis is drawn with the order of bins corresponding to the filling sequence. It is possible to reorder the axis

• alphabetically
• by increasing or decreasing values

The reordering can be triggered via the TAxis context menu by selecting the menu item "LabelsOption" or by calling directly TH1::LabelsOption(option, axis) where

• axis may be "X", "Y" or "Z"
• option may be:
  • "a" sort by alphabetic order
  • ">" sort by decreasing values
  • "<" sort by increasing values
  • "h" draw labels horizontal
  • "v" draw labels vertical
  • "u" draw labels up (end of label right adjusted)
  • "d" draw labels down (start of label left adjusted)

When using the option 2 above, new labels are added by doubling the current number of bins in case one label does not exist yet. When the Filling is terminated, it is possible to trim the number of bins to match the number of active labels by calling

TH1::LabelsDeflate(axis) with axis = "X", "Y" or "Z"

This operation is automatic when using TTree::Draw. Once bin labels have been created, they become persistent if the histogram is written to a file or when generating the C++ code via SavePrimitive.

Histograms with automatic bins

When an histogram is created with an axis lower limit greater or equal to its upper limit, the SetBuffer is automatically called with an argument fBufferSize equal to fgBufferSize (default value=1000). fgBufferSize may be reset via the static function TH1::SetDefaultBufferSize. The axis limits will be automatically computed when the buffer will be full or when the function BufferEmpty is called.

Rebinning

At any time, an histogram can be rebinned via TH1::Rebin. This function returns a new histogram with the rebinned contents. If bin errors were stored, they are recomputed during the rebinning.

Filling histograms

An histogram is typically filled with statements like:

h1->Fill(x);
h1->Fill(x, w); //fill with weight
h2->Fill(x, y)
h2->Fill(x, y, w)
h3->Fill(x, y, z)
h3->Fill(x, y, z, w)

or via one of the Fill functions accepting names described above. The Fill functions compute the bin number corresponding to the given x, y or z argument and increment this bin by the given weight. The Fill functions return the bin number for 1-D histograms or global bin number for 2-D and 3-D histograms. If TH1::Sumw2 has been called before filling, the sum of squares of weights is also stored. One can also increment directly a bin number via TH1::AddBinContent or replace the existing content via TH1::SetBinContent. To access the bin content of a given bin, do:

Double_t binContent = h->GetBinContent(bin);

By default, the bin number is computed using the current axis ranges. If the automatic binning option has been set via

h->SetCanExtend(TH1::kAllAxes);

then, the Fill Function will automatically extend the axis range to accomodate the new value specified in the Fill argument. The method used is to double the bin size until the new value fits in the range, merging bins two by two. This automatic binning options is extensively used by the TTree::Draw function when histogramming Tree variables with an unknown range. This automatic binning option is supported for 1-D, 2-D and 3-D histograms.

During filling, some statistics parameters are incremented to compute the mean value and Root Mean Square with the maximum precision.

In case of histograms of type TH1C, TH1S, TH2C, TH2S, TH3C, TH3S a check is made that the bin contents do not exceed the maximum positive capacity (127 or 32767). Histograms of all types may have positive or/and negative bin contents.

Associated errors

By default, for each bin, the sum of weights is computed at fill time. One can also call TH1::Sumw2 to force the storage and computation of the sum of the square of weights per bin. If Sumw2 has been called, the error per bin is computed as the sqrt(sum of squares of weights), otherwise the error is set equal to the sqrt(bin content). To return the error for a given bin number, do:

Double_t error = h->GetBinError(bin);

Associated functions

One or more object (typically a TF1*) can be added to the list of functions (fFunctions) associated to each histogram. When TH1::Fit is invoked, the fitted function is added to this list. Given an histogram h, one can retrieve an associated function with:

TF1 *myfunc = h->GetFunction("myfunc");

Operations on histograms

Many types of operations are supported on histograms or between histograms

• Addition of an histogram to the current histogram.
• Additions of two histograms with coefficients and storage into the current histogram.
• Multiplications and Divisions are supported in the same way as additions.
• The Add, Divide and Multiply functions also exist to add, divide or multiply an histogram by a function.

If an histogram has associated error bars (TH1::Sumw2 has been called), the resulting error bars are also computed assuming independent histograms. In case of divisions, Binomial errors are also supported. One can mark a histogram to be an "average" histogram by setting its bit kIsAverage via myhist.SetBit(TH1::kIsAverage); When adding (see TH1::Add) average histograms, the histograms are averaged and not summed.

Fitting histograms

Histograms (1-D, 2-D, 3-D and Profiles) can be fitted with a user specified function via TH1::Fit. When an histogram is fitted, the resulting function with its parameters is added to the list of functions of this histogram. If the histogram is made persistent, the list of associated functions is also persistent. Given a pointer (see above) to an associated function myfunc, one can retrieve the function/fit parameters with calls such as:

Double_t chi2 = myfunc->GetChisquare();
Double_t par0 = myfunc->GetParameter(0); value of 1st parameter
Double_t err0 = myfunc->GetParError(0);  error on first parameter

Projections of histograms

One can:

• make a 1-D projection of a 2-D histogram or Profile see functions TH2::ProjectionX,Y, TH2::ProfileX,Y, TProfile::ProjectionX
• make a 1-D, 2-D or profile out of a 3-D histogram see functions TH3::ProjectionZ, TH3::Project3D.

One can fit these projections via:

TH2::FitSlicesX,Y, TH3::FitSlicesZ.

Random Numbers and histograms

TH1::FillRandom can be used to randomly fill an histogram using the contents of an existing TF1 function or another TH1 histogram (for all dimensions). For example the following two statements create and fill an histogram 10000 times with a default gaussian distribution of mean 0 and sigma 1:

TH1F h1("h1", "histo from a gaussian", 100, -3, 3);
h1.FillRandom("gaus", 10000);

TH1::GetRandom can be used to return a random number distributed according the contents of an histogram.

Making a copy of an histogram

Like for any other ROOT object derived from TObject, one can use the Clone() function. This makes an identical copy of the original histogram including all associated errors and functions, e.g.:

TH1F *hnew = (TH1F*)h->Clone("hnew");

Normalizing histograms

One can scale an histogram such that the bins integral is equal to the normalization parameter via TH1::Scale(Double_t norm), where norm is the desired normalization divided by the integral of the histogram.

Drawing histograms

Histograms are drawn via the THistPainter class. Each histogram has a pointer to its own painter (to be usable in a multithreaded program). Many drawing options are supported. See THistPainter::Paint() for more details.

The same histogram can be drawn with different options in different pads. When an histogram drawn in a pad is deleted, the histogram is automatically removed from the pad or pads where it was drawn. If an histogram is drawn in a pad, then filled again, the new status of the histogram will be automatically shown in the pad next time the pad is updated. One does not need to redraw the histogram. To draw the current version of an histogram in a pad, one can use

h->DrawCopy();

This makes a clone (see Clone below) of the histogram. Once the clone is drawn, the original histogram may be modified or deleted without affecting the aspect of the clone.

One can use TH1::SetMaximum() and TH1::SetMinimum() to force a particular value for the maximum or the minimum scale on the plot. (For 1-D histograms this means the y-axis, while for 2-D histograms these functions affect the z-axis).

TH1::UseCurrentStyle() can be used to change all histogram graphics attributes to correspond to the current selected style. This function must be called for each histogram. In case one reads and draws many histograms from a file, one can force the histograms to inherit automatically the current graphics style by calling before gROOT->ForceStyle().

Setting Drawing histogram contour levels (2-D hists only)

By default contours are automatically generated at equidistant intervals. A default value of 20 levels is used. This can be modified via TH1::SetContour() or TH1::SetContourLevel(). the contours level info is used by the drawing options "cont", "surf", and "lego".

Setting histogram graphics attributes

The histogram classes inherit from the attribute classes: TAttLine, TAttFill, and TAttMarker. See the member functions of these classes for the list of options.

Customising how axes are drawn

Use the functions of TAxis, such as

histogram.GetXaxis()->SetTicks("+");
histogram.GetYaxis()->SetRangeUser(1., 5.);

Saving/reading histograms to/from a ROOT file

The following statements create a ROOT file and store an histogram on the file. Because TH1 derives from TNamed, the key identifier on the file is the histogram name:

TFile f("histos.root", "new");
TH1F h1("hgaus", "histo from a gaussian", 100, -3, 3);
h1.FillRandom("gaus", 10000);
h1->Write();

To read this histogram in another Root session, do:

TFile f("histos.root");
TH1F *h = (TH1F*)f.Get("hgaus");

One can save all histograms in memory to the file by:

file->Write();

Miscellaneous operations

TH1::KolmogorovTest(): statistical test of compatibility in shape
                     between two histograms
TH1::Smooth() smooths the bin contents of a 1-d histogram
TH1::Integral() returns the integral of bin contents in a given bin range
TH1::GetMean(int axis) returns the mean value along axis
TH1::GetStdDev(int axis)  returns the sigma distribution along axis
TH1::GetEntries() returns the number of entries
TH1::Reset() resets the bin contents and errors of an histogram

IMPORTANT NOTE: The returned values for GetMean and GetStdDev depend on how the histogram statistics are calculated. By default, if no range has been set, the returned values are the (unbinned) ones calculated at fill time. If a range has been set, however, the values are calculated using the bins in range; THIS IS TRUE EVEN IF THE RANGE INCLUDES ALL BINS–use TAxis::SetRange(0, 0) to unset the range. To ensure that the returned values are always those of the binned data stored in the histogram, call TH1::ResetStats. See TH1::GetStats.

Definition at line 58 of file TH1.h.

Public Types
enum	{   kNoAxis = 0 , kXaxis = BIT(0) , kYaxis = BIT(1) , kZaxis = BIT(2) ,   kAllAxes = kXaxis | kYaxis | kZaxis }
enum	{ kNstat = 13 }
enum	EBinErrorOpt { kNormal = 0 , kPoisson = 1 , kPoisson2 = 2 }
enum	EStatOverflows { kIgnore = 0 , kConsider = 1 , kNeutral = 2 }
	Enumeration specifying the way to treat statoverflow. More...
enum	EStatusBits {   kNoStats = BIT(9) , kUserContour = BIT(10) , kLogX = BIT(15) , kIsZoomed = BIT(16) ,   kNoTitle = BIT(17) , kIsAverage = BIT(18) , kIsNotW = BIT(19) , kAutoBinPTwo = BIT(20) ,   kIsHighlight = BIT(21) }
Public Types inherited from TObject
enum	{   kIsOnHeap = 0x01000000 , kNotDeleted = 0x02000000 , kZombie = 0x04000000 , kInconsistent = 0x08000000 ,   kBitMask = 0x00ffffff }
enum	{ kSingleKey = BIT(0) , kOverwrite = BIT(1) , kWriteDelete = BIT(2) }
enum	EDeprecatedStatusBits { kObjInCanvas = BIT(3) }
enum	EStatusBits {   kCanDelete = BIT(0) , kMustCleanup = BIT(3) , kIsReferenced = BIT(4) , kHasUUID = BIT(5) ,   kCannotPick = BIT(6) , kNoContextMenu = BIT(8) , kInvalidObject = BIT(13) }

Public Member Functions
virtual	~TH1 ()
	Histogram default destructor.
virtual Bool_t	Add (const TH1 *h, const TH1 *h2, Double_t c1=1, Double_t c2=1)
	Replace contents of this histogram by the addition of h1 and h2.
virtual Bool_t	Add (const TH1 *h1, Double_t c1=1)
	Performs the operation: this = this + c1*h1 If errors are defined (see TH1::Sumw2), errors are also recalculated.
virtual Bool_t	Add (TF1 *h1, Double_t c1=1, Option_t *option="")
	Performs the operation: this = this + c1*f1 if errors are defined (see TH1::Sumw2), errors are also recalculated.
virtual void	AddBinContent (Int_t bin)
	Increment bin content by 1.
virtual void	AddBinContent (Int_t bin, Double_t w)
	Increment bin content by a weight w.
virtual Double_t	AndersonDarlingTest (const TH1 *h2, Double_t &advalue) const
	Same function as above but returning also the test statistic value.
virtual Double_t	AndersonDarlingTest (const TH1 *h2, Option_t *option="") const
	Statistical test of compatibility in shape between this histogram and h2, using the Anderson-Darling 2 sample test.
virtual void	Browse (TBrowser *b)
	Browse the Histogram object.
virtual Int_t	BufferEmpty (Int_t action=0)
	Fill histogram with all entries in the buffer.
virtual Bool_t	CanExtendAllAxes () const
	Returns true if all axes are extendable.
virtual Double_t	Chi2Test (const TH1 *h2, Option_t *option="UU", Double_t *res=0) const
	\( \chi^{2} \) test for comparing weighted and unweighted histograms
virtual Double_t	Chi2TestX (const TH1 *h2, Double_t &chi2, Int_t &ndf, Int_t &igood, Option_t *option="UU", Double_t *res=0) const
	The computation routine of the Chisquare test.
virtual Double_t	Chisquare (TF1 *f1, Option_t *option="") const
	Compute and return the chisquare of this histogram with respect to a function The chisquare is computed by weighting each histogram point by the bin error By default the full range of the histogram is used.
virtual void	ClearUnderflowAndOverflow ()
	Remove all the content from the underflow and overflow bins, without changing the number of entries After calling this method, every undeflow and overflow bins will have content 0.0 The Sumw2 is also cleared, since there is no more content in the bins.
TObject *	Clone (const char *newname=0) const
	Make a complete copy of the underlying object.
virtual Double_t	ComputeIntegral (Bool_t onlyPositive=false)
	Compute integral (cumulative sum of bins) The result stored in fIntegral is used by the GetRandom functions.
virtual void	Copy (TObject &hnew) const
	Copy this histogram structure to newth1.
virtual void	DirectoryAutoAdd (TDirectory *)
	Perform the automatic addition of the histogram to the given directory.
virtual Int_t	DistancetoPrimitive (Int_t px, Int_t py)
	Compute distance from point px,py to a line.
virtual Bool_t	Divide (const TH1 *h1)
	Divide this histogram by h1.
virtual Bool_t	Divide (const TH1 *h1, const TH1 *h2, Double_t c1=1, Double_t c2=1, Option_t *option="")
	Replace contents of this histogram by the division of h1 by h2.
virtual Bool_t	Divide (TF1 *f1, Double_t c1=1)
	Performs the operation: this = this/(c1*f1) if errors are defined (see TH1::Sumw2), errors are also recalculated.
virtual void	Draw (Option_t *option="")
	Draw this histogram with options.
virtual TH1 *	DrawCopy (Option_t *option="", const char *name_postfix="_copy") const
	Copy this histogram and Draw in the current pad.
virtual TH1 *	DrawNormalized (Option_t *option="", Double_t norm=1) const
	Draw a normalized copy of this histogram.
virtual void	DrawPanel ()
	Display a panel with all histogram drawing options.
virtual void	Eval (TF1 *f1, Option_t *option="")
	Evaluate function f1 at the center of bins of this histogram.
virtual void	ExecuteEvent (Int_t event, Int_t px, Int_t py)
	Execute action corresponding to one event.
virtual void	ExtendAxis (Double_t x, TAxis *axis)
	Histogram is resized along axis such that x is in the axis range.
virtual TH1 *	FFT (TH1 *h_output, Option_t *option)
	This function allows to do discrete Fourier transforms of TH1 and TH2.
virtual Int_t	Fill (const char *name, Double_t w)
	Increment bin with namex with a weight w.
virtual Int_t	Fill (Double_t x)
	Increment bin with abscissa X by 1.
virtual Int_t	Fill (Double_t x, Double_t w)
	Increment bin with abscissa X with a weight w.
virtual void	FillN (Int_t ntimes, const Double_t *x, const Double_t *w, Int_t stride=1)
	Fill this histogram with an array x and weights w.
virtual void	FillN (Int_t, const Double_t *, const Double_t *, const Double_t *, Int_t)
virtual void	FillRandom (const char *fname, Int_t ntimes=5000, TRandom *rng=nullptr)
	Fill histogram following distribution in function fname.
virtual void	FillRandom (TH1 *h, Int_t ntimes=5000, TRandom *rng=nullptr)
	Fill histogram following distribution in histogram h.
virtual Int_t	FindBin (Double_t x, Double_t y=0, Double_t z=0)
	Return Global bin number corresponding to x,y,z.
virtual Int_t	FindFirstBinAbove (Double_t threshold=0, Int_t axis=1, Int_t firstBin=1, Int_t lastBin=-1) const
	Find first bin with content > threshold for axis (1=x, 2=y, 3=z) if no bins with content > threshold is found the function returns -1.
virtual Int_t	FindFixBin (Double_t x, Double_t y=0, Double_t z=0) const
	Return Global bin number corresponding to x,y,z.
virtual Int_t	FindLastBinAbove (Double_t threshold=0, Int_t axis=1, Int_t firstBin=1, Int_t lastBin=-1) const
	Find last bin with content > threshold for axis (1=x, 2=y, 3=z) if no bins with content > threshold is found the function returns -1.
virtual TObject *	FindObject (const char *name) const
	Search object named name in the list of functions.
virtual TObject *	FindObject (const TObject *obj) const
	Search object obj in the list of functions.
virtual TFitResultPtr	Fit (const char *formula, Option_t *option="", Option_t *goption="", Double_t xmin=0, Double_t xmax=0)
	Fit histogram with function fname.
virtual TFitResultPtr	Fit (TF1 *f1, Option_t *option="", Option_t *goption="", Double_t xmin=0, Double_t xmax=0)
	Fit histogram with function f1.
virtual void	FitPanel ()
	Display a panel with all histogram fit options.
TH1 *	GetAsymmetry (TH1 *h2, Double_t c2=1, Double_t dc2=0)
	Return an histogram containing the asymmetry of this histogram with h2, where the asymmetry is defined as:
virtual Color_t	GetAxisColor (Option_t *axis="X") const
	Return the number of divisions for "axis".
virtual Float_t	GetBarOffset () const
virtual Float_t	GetBarWidth () const
virtual Int_t	GetBin (Int_t binx, Int_t biny=0, Int_t binz=0) const
	Return Global bin number corresponding to binx,y,z.
virtual Double_t	GetBinCenter (Int_t bin) const
	Return bin center for 1D histogram.
virtual Double_t	GetBinContent (Int_t bin) const
	Return content of bin number bin.
virtual Double_t	GetBinContent (Int_t bin, Int_t) const
virtual Double_t	GetBinContent (Int_t bin, Int_t, Int_t) const
virtual Double_t	GetBinError (Int_t bin) const
	Return value of error associated to bin number bin.
virtual Double_t	GetBinError (Int_t binx, Int_t biny) const
virtual Double_t	GetBinError (Int_t binx, Int_t biny, Int_t binz) const
virtual Double_t	GetBinErrorLow (Int_t bin) const
	Return lower error associated to bin number bin.
virtual EBinErrorOpt	GetBinErrorOption () const
virtual Double_t	GetBinErrorUp (Int_t bin) const
	Return upper error associated to bin number bin.
virtual Double_t	GetBinLowEdge (Int_t bin) const
	Return bin lower edge for 1D histogram.
virtual Double_t	GetBinWidth (Int_t bin) const
	Return bin width for 1D histogram.
virtual Double_t	GetBinWithContent (Double_t c, Int_t &binx, Int_t firstx=0, Int_t lastx=0, Double_t maxdiff=0) const
	Compute first binx in the range [firstx,lastx] for which diff = abs(bin_content-c) <= maxdiff.
virtual void	GetBinXYZ (Int_t binglobal, Int_t &binx, Int_t &biny, Int_t &binz) const
	Return binx, biny, binz corresponding to the global bin number globalbin see TH1::GetBin function above.
const Double_t *	GetBuffer () const
Int_t	GetBufferLength () const
Int_t	GetBufferSize () const
virtual Double_t	GetCellContent (Int_t binx, Int_t biny) const
virtual Double_t	GetCellError (Int_t binx, Int_t biny) const
virtual void	GetCenter (Double_t *center) const
	Fill array with center of bins for 1D histogram Better to use h1.GetXaxis()->GetCenter(center)
virtual Int_t	GetContour (Double_t *levels=0)
	Return contour values into array levels if pointer levels is non zero.
virtual Double_t	GetContourLevel (Int_t level) const
	Return value of contour number level.
virtual Double_t	GetContourLevelPad (Int_t level) const
	Return the value of contour number "level" in Pad coordinates.
TH1 *	GetCumulative (Bool_t forward=kTRUE, const char *suffix="_cumulative") const
	Return a pointer to an histogram containing the cumulative content.
virtual Int_t	GetDimension () const
TDirectory *	GetDirectory () const
virtual Double_t	GetEffectiveEntries () const
	Number of effective entries of the histogram.
virtual Double_t	GetEntries () const
	Return the current number of entries.
virtual TF1 *	GetFunction (const char *name) const
	Return pointer to function with name.
virtual Double_t *	GetIntegral ()
	Return a pointer to the array of bins integral.
virtual Double_t	GetKurtosis (Int_t axis=1) const
virtual Color_t	GetLabelColor (Option_t *axis="X") const
	Return the "axis" label color.
virtual Style_t	GetLabelFont (Option_t *axis="X") const
	Return the "axis" label font.
virtual Float_t	GetLabelOffset (Option_t *axis="X") const
	Return the "axis" label offset.
virtual Float_t	GetLabelSize (Option_t *axis="X") const
	Return the "axis" label size.
TList *	GetListOfFunctions () const
virtual void	GetLowEdge (Double_t *edge) const
	Fill array with low edge of bins for 1D histogram Better to use h1.GetXaxis()->GetLowEdge(edge)
virtual Double_t	GetMaximum (Double_t maxval=FLT_MAX) const
	Return maximum value smaller than maxval of bins in the range, unless the value has been overridden by TH1::SetMaximum, in which case it returns that value.
virtual Int_t	GetMaximumBin () const
	Return location of bin with maximum value in the range.
virtual Int_t	GetMaximumBin (Int_t &locmax, Int_t &locmay, Int_t &locmaz) const
	Return location of bin with maximum value in the range.
virtual Double_t	GetMaximumStored () const
virtual Double_t	GetMean (Int_t axis=1) const
	For axis = 1,2 or 3 returns the mean value of the histogram along X,Y or Z axis.
virtual Double_t	GetMeanError (Int_t axis=1) const
	Return standard error of mean of this histogram along the X axis.
virtual Double_t	GetMinimum (Double_t minval=-FLT_MAX) const
	Return minimum value larger than minval of bins in the range, unless the value has been overridden by TH1::SetMinimum, in which case it returns that value.
virtual void	GetMinimumAndMaximum (Double_t &min, Double_t &max) const
	Retrieve the minimum and maximum values in the histogram.
virtual Int_t	GetMinimumBin () const
	Return location of bin with minimum value in the range.
virtual Int_t	GetMinimumBin (Int_t &locmix, Int_t &locmiy, Int_t &locmiz) const
	Return location of bin with minimum value in the range.
virtual Double_t	GetMinimumStored () const
virtual Int_t	GetNbinsX () const
virtual Int_t	GetNbinsY () const
virtual Int_t	GetNbinsZ () const
virtual Int_t	GetNcells () const
virtual Int_t	GetNdivisions (Option_t *axis="X") const
	Return the number of divisions for "axis".
virtual Double_t	GetNormFactor () const
virtual char *	GetObjectInfo (Int_t px, Int_t py) const
	Redefines TObject::GetObjectInfo.
Option_t *	GetOption () const
TVirtualHistPainter *	GetPainter (Option_t *option="")
	Return pointer to painter.
virtual Int_t	GetQuantiles (Int_t nprobSum, Double_t *q, const Double_t *probSum=0)
	Compute Quantiles for this histogram Quantile x_q of a probability distribution Function F is defined as.
virtual Double_t	GetRandom (TRandom *rng=nullptr) const
	Return a random number distributed according the histogram bin contents.
Double_t	GetRMS (Int_t axis=1) const
Double_t	GetRMSError (Int_t axis=1) const
virtual Double_t	GetSkewness (Int_t axis=1) const
EStatOverflows	GetStatOverflows () const
virtual void	GetStats (Double_t *stats) const
	fill the array stats from the contents of this histogram The array stats must be correctly dimensioned in the calling program.
virtual Double_t	GetStdDev (Int_t axis=1) const
	Returns the Standard Deviation (Sigma).
virtual Double_t	GetStdDevError (Int_t axis=1) const
	Return error of standard deviation estimation for Normal distribution.
virtual Double_t	GetSumOfWeights () const
	Return the sum of weights excluding under/overflows.
virtual TArrayD *	GetSumw2 ()
virtual const TArrayD *	GetSumw2 () const
virtual Int_t	GetSumw2N () const
virtual Float_t	GetTickLength (Option_t *axis="X") const
	Return the "axis" tick length.
virtual Style_t	GetTitleFont (Option_t *axis="X") const
	Return the "axis" title font.
virtual Float_t	GetTitleOffset (Option_t *axis="X") const
	Return the "axis" title offset.
virtual Float_t	GetTitleSize (Option_t *axis="X") const
	Return the "axis" title size.
TAxis *	GetXaxis ()
	Get the behaviour adopted by the object about the statoverflows. See EStatOverflows for more information.
const TAxis *	GetXaxis () const
TAxis *	GetYaxis ()
const TAxis *	GetYaxis () const
TAxis *	GetZaxis ()
const TAxis *	GetZaxis () const
virtual Double_t	Integral (Int_t binx1, Int_t binx2, Option_t *option="") const
	Return integral of bin contents in range [binx1,binx2].
virtual Double_t	Integral (Option_t *option="") const
	Return integral of bin contents.
virtual Double_t	IntegralAndError (Int_t binx1, Int_t binx2, Double_t &err, Option_t *option="") const
	Return integral of bin contents in range [binx1,binx2] and its error.
virtual Double_t	Interpolate (Double_t x) const
	Given a point x, approximates the value via linear interpolation based on the two nearest bin centers.
virtual Double_t	Interpolate (Double_t x, Double_t y) const
	2d Interpolation. Not yet implemented.
virtual Double_t	Interpolate (Double_t x, Double_t y, Double_t z) const
	3d Interpolation. Not yet implemented.
Bool_t	IsBinOverflow (Int_t bin, Int_t axis=0) const
	Return true if the bin is overflow.
Bool_t	IsBinUnderflow (Int_t bin, Int_t axis=0) const
	Return true if the bin is underflow.
virtual Bool_t	IsHighlight () const
virtual Double_t	KolmogorovTest (const TH1 *h2, Option_t *option="") const
	Statistical test of compatibility in shape between this histogram and h2, using Kolmogorov test.
virtual void	LabelsDeflate (Option_t *axis="X")
	Reduce the number of bins for the axis passed in the option to the number of bins having a label.
virtual void	LabelsInflate (Option_t *axis="X")
	Double the number of bins for axis.
virtual void	LabelsOption (Option_t *option="h", Option_t *axis="X")
	Sort bins with labels or set option(s) to draw axis with labels.
virtual Long64_t	Merge (TCollection *list)
Long64_t	Merge (TCollection *list, Option_t *option)
	Add all histograms in the collection to this histogram.
virtual Bool_t	Multiply (const TH1 *h1)
	Multiply this histogram by h1.
virtual Bool_t	Multiply (const TH1 *h1, const TH1 *h2, Double_t c1=1, Double_t c2=1, Option_t *option="")
	Replace contents of this histogram by multiplication of h1 by h2.
virtual Bool_t	Multiply (TF1 *f1, Double_t c1=1)
	Performs the operation:
virtual void	Paint (Option_t *option="")
	Control routine to paint any kind of histograms.
virtual void	Print (Option_t *option="") const
	Print some global quantities for this histogram.
virtual void	PutStats (Double_t *stats)
	Replace current statistics with the values in array stats.
virtual TH1 *	Rebin (Int_t ngroup=2, const char *newname="", const Double_t *xbins=0)
	Rebin this histogram.
virtual void	RebinAxis (Double_t x, TAxis *axis)
virtual TH1 *	RebinX (Int_t ngroup=2, const char *newname="")
virtual void	Rebuild (Option_t *option="")
	Using the current bin info, recompute the arrays for contents and errors.
virtual void	RecursiveRemove (TObject *obj)
	Recursively remove object from the list of functions.
virtual void	Reset (Option_t *option="")
	Reset this histogram: contents, errors, etc.
virtual void	ResetStats ()
	Reset the statistics including the number of entries and replace with values calculated from bin content.
virtual void	SavePrimitive (std::ostream &out, Option_t *option="")
	Save primitive as a C++ statement(s) on output stream out.
virtual void	Scale (Double_t c1=1, Option_t *option="")
	Multiply this histogram by a constant c1.
virtual void	SetAxisColor (Color_t color=1, Option_t *axis="X")
	Set color to draw the axis line and tick marks.
virtual void	SetAxisRange (Double_t xmin, Double_t xmax, Option_t *axis="X")
	Set the "axis" range.
virtual void	SetBarOffset (Float_t offset=0.25)
	Set the bar offset as fraction of the bin width for drawing mode "B".
virtual void	SetBarWidth (Float_t width=0.5)
	Set the width of bars as fraction of the bin width for drawing mode "B".
virtual void	SetBinContent (Int_t bin, Double_t content)
	Set bin content see convention for numbering bins in TH1::GetBin In case the bin number is greater than the number of bins and the timedisplay option is set or CanExtendAllAxes(), the number of bins is automatically doubled to accommodate the new bin.
virtual void	SetBinContent (Int_t bin, Int_t, Double_t content)
virtual void	SetBinContent (Int_t bin, Int_t, Int_t, Double_t content)
virtual void	SetBinError (Int_t bin, Double_t error)
	Set the bin Error Note that this resets the bin eror option to be of Normal Type and for the non-empty bin the bin error is set by default to the square root of their content.
virtual void	SetBinError (Int_t binx, Int_t biny, Double_t error)
	See convention for numbering bins in TH1::GetBin.
virtual void	SetBinError (Int_t binx, Int_t biny, Int_t binz, Double_t error)
	See convention for numbering bins in TH1::GetBin.
virtual void	SetBinErrorOption (EBinErrorOpt type)
virtual void	SetBins (Int_t nx, const Double_t *xBins)
	Redefine x axis parameters with variable bin sizes.
virtual void	SetBins (Int_t nx, const Double_t *xBins, Int_t ny, const Double_t *yBins)
	Redefine x and y axis parameters with variable bin sizes.
virtual void	SetBins (Int_t nx, const Double_t *xBins, Int_t ny, const Double_t *yBins, Int_t nz, const Double_t *zBins)
	Redefine x, y and z axis parameters with variable bin sizes.
virtual void	SetBins (Int_t nx, Double_t xmin, Double_t xmax)
	Redefine x axis parameters.
virtual void	SetBins (Int_t nx, Double_t xmin, Double_t xmax, Int_t ny, Double_t ymin, Double_t ymax)
	Redefine x and y axis parameters.
virtual void	SetBins (Int_t nx, Double_t xmin, Double_t xmax, Int_t ny, Double_t ymin, Double_t ymax, Int_t nz, Double_t zmin, Double_t zmax)
	Redefine x, y and z axis parameters.
virtual void	SetBinsLength (Int_t=-1)
virtual void	SetBuffer (Int_t buffersize, Option_t *option="")
	Set the maximum number of entries to be kept in the buffer.
virtual UInt_t	SetCanExtend (UInt_t extendBitMask)
	Make the histogram axes extendable / not extendable according to the bit mask returns the previous bit mask specifying which axes are extendable.
virtual void	SetCellContent (Int_t binx, Int_t biny, Double_t content)
virtual void	SetCellError (Int_t binx, Int_t biny, Double_t content)
virtual void	SetContent (const Double_t *content)
	Replace bin contents by the contents of array content.
virtual void	SetContour (Int_t nlevels, const Double_t *levels=0)
	Set the number and values of contour levels.
virtual void	SetContourLevel (Int_t level, Double_t value)
	Set value for one contour level.
virtual void	SetDirectory (TDirectory *dir)
	By default when an histogram is created, it is added to the list of histogram objects in the current directory in memory.
virtual void	SetEntries (Double_t n)
virtual void	SetError (const Double_t *error)
	Replace bin errors by values in array error.
virtual void	SetHighlight (Bool_t set=kTRUE)
	Set highlight (enable/disable) mode for the histogram by default highlight mode is disable.
virtual void	SetLabelColor (Color_t color=1, Option_t *axis="X")
	Set axis labels color.
virtual void	SetLabelFont (Style_t font=62, Option_t *axis="X")
	Set font number used to draw axis labels.
virtual void	SetLabelOffset (Float_t offset=0.005, Option_t *axis="X")
	Set offset between axis and axis' labels.
virtual void	SetLabelSize (Float_t size=0.02, Option_t *axis="X")
	Set size of axis' labels.
virtual void	SetMaximum (Double_t maximum=-1111)
virtual void	SetMinimum (Double_t minimum=-1111)
virtual void	SetName (const char *name)
	Change the name of this histogram.
virtual void	SetNameTitle (const char *name, const char *title)
	Change the name and title of this histogram.
virtual void	SetNdivisions (Int_t n=510, Option_t *axis="X")
	Set the number of divisions to draw an axis.
virtual void	SetNormFactor (Double_t factor=1)
virtual void	SetOption (Option_t *option=" ")
void	SetStatOverflows (EStatOverflows statOverflows)
virtual void	SetStats (Bool_t stats=kTRUE)
	Set statistics option on/off.
virtual void	SetTickLength (Float_t length=0.02, Option_t *axis="X")
	Set the axis' tick marks length.
virtual void	SetTitle (const char *title)
	See GetStatOverflows for more information.
virtual void	SetTitleFont (Style_t font=62, Option_t *axis="X")
	Set the axis' title font.
virtual void	SetTitleOffset (Float_t offset=1, Option_t *axis="X")
	Specify a parameter offset to control the distance between the axis and the axis' title.
virtual void	SetTitleSize (Float_t size=0.02, Option_t *axis="X")
	Set the axis' title size.
virtual void	SetXTitle (const char *title)
virtual void	SetYTitle (const char *title)
virtual void	SetZTitle (const char *title)
virtual TH1 *	ShowBackground (Int_t niter=20, Option_t *option="same")
	This function calculates the background spectrum in this histogram.
virtual Int_t	ShowPeaks (Double_t sigma=2, Option_t *option="", Double_t threshold=0.05)
	Interface to TSpectrum::Search.
virtual void	Smooth (Int_t ntimes=1, Option_t *option="")
	Smooth bin contents of this histogram.
virtual void	Sumw2 (Bool_t flag=kTRUE)
	Create structure to store sum of squares of weights.
void	UseCurrentStyle ()
	Copy current attributes from/to current style.
Public Member Functions inherited from TNamed
	TNamed ()
	TNamed (const char *name, const char *title)
	TNamed (const TNamed &named)
	TNamed copy ctor.
	TNamed (const TString &name, const TString &title)
virtual	~TNamed ()
	TNamed destructor.
virtual void	Clear (Option_t *option="")
	Set name and title to empty strings ("").
virtual Int_t	Compare (const TObject *obj) const
	Compare two TNamed objects.
virtual void	FillBuffer (char *&buffer)
	Encode TNamed into output buffer.
virtual const char *	GetName () const
	Returns name of object.
virtual const char *	GetTitle () const
	Returns title of object.
virtual ULong_t	Hash () const
	Return hash value for this object.
virtual Bool_t	IsSortable () const
virtual void	ls (Option_t *option="") const
	List TNamed name and title.
TNamed &	operator= (const TNamed &rhs)
	TNamed assignment operator.
virtual Int_t	Sizeof () const
	Return size of the TNamed part of the TObject.
Public Member Functions inherited from TObject
	TObject ()
	TObject constructor.
	TObject (const TObject &object)
	TObject copy ctor.
virtual	~TObject ()
	TObject destructor.
void	AbstractMethod (const char *method) const
	Use this method to implement an "abstract" method that you don't want to leave purely abstract.
virtual void	AppendPad (Option_t *option="")
	Append graphics object to current pad.
ULong_t	CheckedHash ()
	Check and record whether this class has a consistent Hash/RecursiveRemove setup (*) and then return the regular Hash value for this object.
virtual const char *	ClassName () const
	Returns name of class to which the object belongs.
virtual void	Delete (Option_t *option="")
	Delete this object.
virtual void	DrawClass () const
	Draw class inheritance tree of the class to which this object belongs.
virtual TObject *	DrawClone (Option_t *option="") const
	Draw a clone of this object in the current selected pad for instance with: gROOT->SetSelectedPad(gPad).
virtual void	Dump () const
	Dump contents of object on stdout.
virtual void	Error (const char *method, const char *msgfmt,...) const
	Issue error message.
virtual void	Execute (const char *method, const char *params, Int_t *error=0)
	Execute method on this object with the given parameter string, e.g.
virtual void	Execute (TMethod *method, TObjArray *params, Int_t *error=0)
	Execute method on this object with parameters stored in the TObjArray.
virtual void	Fatal (const char *method, const char *msgfmt,...) const
	Issue fatal error message.
virtual Option_t *	GetDrawOption () const
	Get option used by the graphics system to draw this object.
virtual const char *	GetIconName () const
	Returns mime type name of object.
virtual UInt_t	GetUniqueID () const
	Return the unique object id.
virtual Bool_t	HandleTimer (TTimer *timer)
	Execute action in response of a timer timing out.
Bool_t	HasInconsistentHash () const
	Return true is the type of this object is known to have an inconsistent setup for Hash and RecursiveRemove (i.e.
virtual void	Info (const char *method, const char *msgfmt,...) const
	Issue info message.
virtual Bool_t	InheritsFrom (const char *classname) const
	Returns kTRUE if object inherits from class "classname".
virtual Bool_t	InheritsFrom (const TClass *cl) const
	Returns kTRUE if object inherits from TClass cl.
virtual void	Inspect () const
	Dump contents of this object in a graphics canvas.
void	InvertBit (UInt_t f)
virtual Bool_t	IsEqual (const TObject *obj) const
	Default equal comparison (objects are equal if they have the same address in memory).
virtual Bool_t	IsFolder () const
	Returns kTRUE in case object contains browsable objects (like containers or lists of other objects).
R__ALWAYS_INLINE Bool_t	IsOnHeap () const
R__ALWAYS_INLINE Bool_t	IsZombie () const
void	MayNotUse (const char *method) const
	Use this method to signal that a method (defined in a base class) may not be called in a derived class (in principle against good design since a child class should not provide less functionality than its parent, however, sometimes it is necessary).
virtual Bool_t	Notify ()
	This method must be overridden to handle object notification.
void	Obsolete (const char *method, const char *asOfVers, const char *removedFromVers) const
	Use this method to declare a method obsolete.
void	operator delete (void *ptr)
	Operator delete.
void	operator delete[] (void *ptr)
	Operator delete [].
void *	operator new (size_t sz)
void *	operator new (size_t sz, void *vp)
void *	operator new[] (size_t sz)
void *	operator new[] (size_t sz, void *vp)
TObject &	operator= (const TObject &rhs)
	TObject assignment operator.
virtual void	Pop ()
	Pop on object drawn in a pad to the top of the display list.
virtual Int_t	Read (const char *name)
	Read contents of object with specified name from the current directory.
void	ResetBit (UInt_t f)
virtual void	SaveAs (const char *filename="", Option_t *option="") const
	Save this object in the file specified by filename.
void	SetBit (UInt_t f)
void	SetBit (UInt_t f, Bool_t set)
	Set or unset the user status bits as specified in f.
virtual void	SetDrawOption (Option_t *option="")
	Set drawing option for object.
virtual void	SetUniqueID (UInt_t uid)
	Set the unique object id.
virtual void	SysError (const char *method, const char *msgfmt,...) const
	Issue system error message.
R__ALWAYS_INLINE Bool_t	TestBit (UInt_t f) const
Int_t	TestBits (UInt_t f) const
virtual void	Warning (const char *method, const char *msgfmt,...) const
	Issue warning message.
virtual Int_t	Write (const char *name=0, Int_t option=0, Int_t bufsize=0)
	Write this object to the current directory.
virtual Int_t	Write (const char *name=0, Int_t option=0, Int_t bufsize=0) const
	Write this object to the current directory.
Public Member Functions inherited from TAttLine
	TAttLine ()
	AttLine default constructor.
	TAttLine (Color_t lcolor, Style_t lstyle, Width_t lwidth)
	AttLine normal constructor.
virtual	~TAttLine ()
	AttLine destructor.
void	Copy (TAttLine &attline) const
	Copy this line attributes to a new TAttLine.
Int_t	DistancetoLine (Int_t px, Int_t py, Double_t xp1, Double_t yp1, Double_t xp2, Double_t yp2)
	Compute distance from point px,py to a line.
virtual Color_t	GetLineColor () const
	Return the line color.
virtual Style_t	GetLineStyle () const
	Return the line style.
virtual Width_t	GetLineWidth () const
	Return the line width.
virtual void	Modify ()
	Change current line attributes if necessary.
virtual void	ResetAttLine (Option_t *option="")
	Reset this line attributes to default values.
virtual void	SaveLineAttributes (std::ostream &out, const char *name, Int_t coldef=1, Int_t stydef=1, Int_t widdef=1)
	Save line attributes as C++ statement(s) on output stream out.
virtual void	SetLineAttributes ()
	Invoke the DialogCanvas Line attributes.
virtual void	SetLineColor (Color_t lcolor)
	Set the line color.
virtual void	SetLineColorAlpha (Color_t lcolor, Float_t lalpha)
	Set a transparent line color.
virtual void	SetLineStyle (Style_t lstyle)
	Set the line style.
virtual void	SetLineWidth (Width_t lwidth)
	Set the line width.
Public Member Functions inherited from TAttFill
	TAttFill ()
	AttFill default constructor.
	TAttFill (Color_t fcolor, Style_t fstyle)
	AttFill normal constructor.
virtual	~TAttFill ()
	AttFill destructor.
void	Copy (TAttFill &attfill) const
	Copy this fill attributes to a new TAttFill.
virtual Color_t	GetFillColor () const
	Return the fill area color.
virtual Style_t	GetFillStyle () const
	Return the fill area style.
virtual Bool_t	IsTransparent () const
virtual void	Modify ()
	Change current fill area attributes if necessary.
virtual void	ResetAttFill (Option_t *option="")
	Reset this fill attributes to default values.
virtual void	SaveFillAttributes (std::ostream &out, const char *name, Int_t coldef=1, Int_t stydef=1001)
	Save fill attributes as C++ statement(s) on output stream out.
virtual void	SetFillAttributes ()
	Invoke the DialogCanvas Fill attributes.
virtual void	SetFillColor (Color_t fcolor)
	Set the fill area color.
virtual void	SetFillColorAlpha (Color_t fcolor, Float_t falpha)
	Set a transparent fill color.
virtual void	SetFillStyle (Style_t fstyle)
	Set the fill area style.
Public Member Functions inherited from TAttMarker
	TAttMarker ()
	TAttMarker default constructor.
	TAttMarker (Color_t color, Style_t style, Size_t msize)
	TAttMarker normal constructor.
virtual	~TAttMarker ()
	TAttMarker destructor.
void	Copy (TAttMarker &attmarker) const
	Copy this marker attributes to a new TAttMarker.
virtual Color_t	GetMarkerColor () const
	Return the marker color.
virtual Size_t	GetMarkerSize () const
	Return the marker size.
virtual Style_t	GetMarkerStyle () const
	Return the marker style.
virtual void	Modify ()
	Change current marker attributes if necessary.
virtual void	ResetAttMarker (Option_t *toption="")
	Reset this marker attributes to the default values.
virtual void	SaveMarkerAttributes (std::ostream &out, const char *name, Int_t coldef=1, Int_t stydef=1, Int_t sizdef=1)
	Save line attributes as C++ statement(s) on output stream out.
virtual void	SetMarkerAttributes ()
	Invoke the DialogCanvas Marker attributes.
virtual void	SetMarkerColor (Color_t mcolor=1)
	Set the marker color.
virtual void	SetMarkerColorAlpha (Color_t mcolor, Float_t malpha)
	Set a transparent marker color.
virtual void	SetMarkerSize (Size_t msize=1)
	Set the marker size.
virtual void	SetMarkerStyle (Style_t mstyle=1)
	Set the marker style.

Static Public Member Functions
static void	AddDirectory (Bool_t add=kTRUE)
	Sets the flag controlling the automatic add of histograms in memory.
static Bool_t	AddDirectoryStatus ()
	Static function: cannot be inlined on Windows/NT.
static Int_t	FitOptionsMake (Option_t *option, Foption_t &Foption)
	Decode string choptin and fill fitOption structure.
static Int_t	GetDefaultBufferSize ()
	Static function return the default buffer size for automatic histograms the parameter fgBufferSize may be changed via SetDefaultBufferSize.
static Bool_t	GetDefaultSumw2 ()
	Return kTRUE if TH1::Sumw2 must be called when creating new histograms.
static void	SetDefaultBufferSize (Int_t buffersize=1000)
	Static function to set the default buffer size for automatic histograms.
static void	SetDefaultSumw2 (Bool_t sumw2=kTRUE)
	When this static function is called with sumw2=kTRUE, all new histograms will automatically activate the storage of the sum of squares of errors, ie TH1::Sumw2 is automatically called.
static void	SmoothArray (Int_t NN, Double_t *XX, Int_t ntimes=1)
	Smooth array xx, translation of Hbook routine hsmoof.F based on algorithm 353QH twice presented by J.
static void	StatOverflows (Bool_t flag=kTRUE)
	if flag=kTRUE, underflows and overflows are used by the Fill functions in the computation of statistics (mean value, StdDev).
static TH1 *	TransformHisto (TVirtualFFT *fft, TH1 *h_output, Option_t *option)
	For a given transform (first parameter), fills the histogram (second parameter) with the transform output data, specified in the third parameter If the 2nd parameter h_output is empty, a new histogram (TH1D or TH2D) is created and the user is responsible for deleting it.
Static Public Member Functions inherited from TObject
static Long_t	GetDtorOnly ()
	Return destructor only flag.
static Bool_t	GetObjectStat ()
	Get status of object stat flag.
static void	SetDtorOnly (void *obj)
	Set destructor only flag.
static void	SetObjectStat (Bool_t stat)
	Turn on/off tracking of objects in the TObjectTable.
Static Public Member Functions inherited from TAttMarker
static Width_t	GetMarkerLineWidth (Style_t style)
	Internal helper function that returns the line width of the given marker style (0 = filled marker)
static Style_t	GetMarkerStyleBase (Style_t style)
	Internal helper function that returns the corresponding marker style with line width 1 for the given style.

Protected Member Functions
	TH1 ()
	Histogram default constructor.
	TH1 (const char *name, const char *title, Int_t nbinsx, const Double_t *xbins)
	Normal constructor for variable bin size histograms.
	TH1 (const char *name, const char *title, Int_t nbinsx, const Float_t *xbins)
	Normal constructor for variable bin size histograms.
	TH1 (const char *name, const char *title, Int_t nbinsx, Double_t xlow, Double_t xup)
	Normal constructor for fix bin size histograms.
virtual Int_t	AutoP2FindLimits (Double_t min, Double_t max)
	Buffer-based estimate of the histogram range using the power of 2 algorithm.
Int_t	AxisChoice (Option_t *axis) const
	Choose an axis according to "axis".
virtual Int_t	BufferFill (Double_t x, Double_t w)
	accumulate arguments in buffer.
virtual void	DoFillN (Int_t ntimes, const Double_t *x, const Double_t *w, Int_t stride=1)
	Internal method to fill histogram content from a vector called directly by TH1::BufferEmpty.
virtual Double_t	DoIntegral (Int_t ix1, Int_t ix2, Int_t iy1, Int_t iy2, Int_t iz1, Int_t iz2, Double_t &err, Option_t *opt, Bool_t doerr=kFALSE) const
	Internal function compute integral and optionally the error between the limits specified by the bin number values working for all histograms (1D, 2D and 3D)
virtual Bool_t	FindNewAxisLimits (const TAxis *axis, const Double_t point, Double_t &newMin, Double_t &newMax)
	finds new limits for the axis so that point is within the range and the limits are compatible with the previous ones (see TH1::Merge).
UInt_t	GetAxisLabelStatus () const
	Internal function used in TH1::Fill to see which axis is full alphanumeric i.e.
virtual Double_t	GetBinErrorSqUnchecked (Int_t bin) const
Bool_t	GetStatOverflowsBehaviour () const
Bool_t	IsEmpty () const
	Check if an histogram is empty (this a protected method used mainly by TH1Merger )
virtual Double_t	RetrieveBinContent (Int_t bin) const
	Raw retrieval of bin content on internal data structure see convention for numbering bins in TH1::GetBin.
virtual void	SavePrimitiveHelp (std::ostream &out, const char *hname, Option_t *option="")
	Helper function for the SavePrimitive functions from TH1 or classes derived from TH1, eg TProfile, TProfile2D.
virtual void	UpdateBinContent (Int_t bin, Double_t content)
	Raw update of bin content on internal data structure see convention for numbering bins in TH1::GetBin.
Protected Member Functions inherited from TObject
virtual void	DoError (int level, const char *location, const char *fmt, va_list va) const
	Interface to ErrorHandler (protected).
void	MakeZombie ()

Static Protected Member Functions
static Int_t	AutoP2GetBins (Int_t n)
	Auxiliary function to get the next power of 2 integer value larger then n.
static Double_t	AutoP2GetPower2 (Double_t x, Bool_t next=kTRUE)
	Auxiliary function to get the power of 2 next (larger) or previous (smaller) a given x.
static bool	CheckAxisLimits (const TAxis *a1, const TAxis *a2)
	Check that the axis limits of the histograms are the same.
static bool	CheckBinLabels (const TAxis *a1, const TAxis *a2)
	Check that axis have same labels.
static bool	CheckBinLimits (const TAxis *a1, const TAxis *a2)
	Check bin limits.
static bool	CheckConsistency (const TH1 *h1, const TH1 *h2)
	Check histogram compatibility.
static bool	CheckConsistentSubAxes (const TAxis *a1, Int_t firstBin1, Int_t lastBin1, const TAxis *a2, Int_t firstBin2=0, Int_t lastBin2=0)
	Check that two sub axis are the same.
static bool	CheckEqualAxes (const TAxis *a1, const TAxis *a2)
	Check that the axis are the same.
static Bool_t	RecomputeAxisLimits (TAxis &destAxis, const TAxis &anAxis)
	Finds new limits for the axis for the Merge function.
static Bool_t	SameLimitsAndNBins (const TAxis &axis1, const TAxis &axis2)
	Same limits and bins.

Protected Attributes
Short_t	fBarOffset
	(1000*offset) for bar charts or legos
Short_t	fBarWidth
	(1000*width) for bar charts or legos
EBinErrorOpt	fBinStatErrOpt
	option for bin statistical errors
Double_t *	fBuffer
	[fBufferSize] entry buffer
Int_t	fBufferSize
	fBuffer size
TArrayD	fContour
	Array to display contour levels.
Int_t	fDimension
	!Histogram dimension (1, 2 or 3 dim)
TDirectory *	fDirectory
	!Pointer to directory holding this histogram
Double_t	fEntries
	Number of entries.
TList *	fFunctions
	->Pointer to list of functions (fits and user)
Double_t *	fIntegral
	!Integral of bins used by GetRandom
Double_t	fMaximum
	Maximum value for plotting.
Double_t	fMinimum
	Minimum value for plotting.
Int_t	fNcells
	number of bins(1D), cells (2D) +U/Overflows
Double_t	fNormFactor
	Normalization factor.
TString	fOption
	histogram options
TVirtualHistPainter *	fPainter
	!pointer to histogram painter
EStatOverflows	fStatOverflows
	per object flag to use under/overflows in statistics
TArrayD	fSumw2
	Array of sum of squares of weights.
Double_t	fTsumw
	Total Sum of weights.
Double_t	fTsumw2
	Total Sum of squares of weights.
Double_t	fTsumwx
	Total Sum of weight*X.
Double_t	fTsumwx2
	Total Sum of weight*X*X.
TAxis	fXaxis
	X axis descriptor.
TAxis	fYaxis
	Y axis descriptor.
TAxis	fZaxis
	Z axis descriptor.
Protected Attributes inherited from TNamed
TString	fName
TString	fTitle
Protected Attributes inherited from TAttLine
Color_t	fLineColor
	Line color.
Style_t	fLineStyle
	Line style.
Width_t	fLineWidth
	Line width.
Protected Attributes inherited from TAttFill
Color_t	fFillColor
	Fill area color.
Style_t	fFillStyle
	Fill area style.
Protected Attributes inherited from TAttMarker
Color_t	fMarkerColor
	Marker color.
Size_t	fMarkerSize
	Marker size.
Style_t	fMarkerStyle
	Marker style.

Static Protected Attributes
static Bool_t	fgAddDirectory = kTRUE
	!flag to add histograms to the directory
static Int_t	fgBufferSize = 1000
	!default buffer size for automatic histograms
static Bool_t	fgDefaultSumw2 = kFALSE
	!flag to call TH1::Sumw2 automatically at histogram creation time
static Bool_t	fgStatOverflows = kFALSE
	!flag to use under/overflows in statistics

Private Member Functions
	TH1 (const TH1 &)
	Copy constructor.
void	Build ()
	Creates histogram basic data structure.
TH1 &	operator= (const TH1 &)

Friends
class	TH1Merger

Additional Inherited Members
Protected Types inherited from TObject
enum	{ kOnlyPrepStep = BIT(3) }

#include <TH1.h>

Inheritance diagram for TH1:

Member Enumeration Documentation

anonymous enum

anonymous enum

Enumerator
kNoAxis	NOTE: Must always be 0 !!!
kXaxis
kYaxis
kZaxis
kAllAxes

Definition at line 70 of file TH1.h.

anonymous enum

anonymous enum

Enumerator
kNstat

Definition at line 182 of file TH1.h.

EBinErrorOpt

enum TH1::EBinErrorOpt

Enumerator
kNormal	errors with Normal (Wald) approximation: errorUp=errorLow= sqrt(N)
kPoisson	errors from Poisson interval at 68.3% (1 sigma)
kPoisson2	errors from Poisson interval at 95% CL (~ 2 sigma)

Definition at line 63 of file TH1.h.

EStatOverflows

enum TH1::EStatOverflows

Enumeration specifying the way to treat statoverflow.

Enumerator
kIgnore	Override global flag ignoring the overflows.
kConsider	Override global flag considering the overflows.
kNeutral	Adapt to the global flag.

Definition at line 79 of file TH1.h.

EStatusBits

enum TH1::EStatusBits

Enumerator
kNoStats	don't draw stats box
kUserContour	user specified contour levels
kLogX	X-axis in log scale.
kIsZoomed	bit set when zooming on Y axis
kNoTitle	don't draw the histogram title
kIsAverage	Bin contents are average (used by Add)
kIsNotW	Histogram is forced to be not weighted even when the histogram is filled with weighted different than 1.
kAutoBinPTwo	Use Power(2)-based algorithm for autobinning.
kIsHighlight	bit set if histo is highlight

Definition at line 163 of file TH1.h.

Constructor & Destructor Documentation

TH1() [1/5]

TH1::TH1 ( const TH1 &  h )

private

Copy constructor.

The list of functions is not copied. (Use Clone if needed)

Definition at line 742 of file TH1.cxx.

TH1() [2/5]

TH1::TH1 ( )

protected

Histogram default constructor.

Definition at line 595 of file TH1.cxx.

TH1() [3/5]

TH1::TH1 ( const char *  name, const char *  title, Int_t  nbins, Double_t  xlow, Double_t  xup  )

protected

Normal constructor for fix bin size histograms.

Creates the main histogram structure.

Parameters

[in]	name	name of histogram (avoid blanks)
[in]	title	histogram title. If title is of the form stringt;stringx;stringy;stringz, the histogram title is set to stringt, the x axis title to stringx, the y axis title to stringy, etc.
[in]	nbins	number of bins
[in]	xlow	low edge of first bin
[in]	xup	upper edge of last bin (not included in last bin)

When an histogram is created, it is automatically added to the list of special objects in the current directory. To find the pointer to this histogram in the current directory by its name, do:

TH1F *h1 = (TH1F*)gDirectory->FindObject(name);

Definition at line 684 of file TH1.cxx.

TH1() [4/5]

TH1::TH1 ( const char *  name, const char *  title, Int_t  nbins, const Float_t *  xbins  )

protected

Normal constructor for variable bin size histograms.

Creates the main histogram structure.

Parameters

[in]	name	name of histogram (avoid blanks)
[in]	title	histogram title. If title is of the form stringt;stringx;stringy;stringz the histogram title is set to stringt, the x axis title to stringx, the y axis title to stringy, etc.
[in]	nbins	number of bins
[in]	xbins	array of low-edges for each bin. This is an array of size nbins+1

Definition at line 706 of file TH1.cxx.

TH1() [5/5]

TH1::TH1 ( const char *  name, const char *  title, Int_t  nbins, const Double_t *  xbins  )

protected

Normal constructor for variable bin size histograms.

Parameters

[in]	name	name of histogram (avoid blanks)
[in]	title	histogram title. If title is of the form stringt;stringx;stringy;stringz the histogram title is set to stringt, the x axis title to stringx, the y axis title to stringy, etc.
[in]	nbins	number of bins
[in]	xbins	array of low-edges for each bin. This is an array of size nbins+1

Definition at line 728 of file TH1.cxx.

~TH1()

TH1::~TH1 ( )

virtual

Histogram default destructor.

Definition at line 623 of file TH1.cxx.

Member Function Documentation

Add() [1/3]

Bool_t TH1::Add ( const TH1 *  h1, const TH1 *  h2, Double_t  c1 = 1, Double_t  c2 = 1  )

virtual

Replace contents of this histogram by the addition of h1 and h2.

this = c1*h1 + c2*h2 if errors are defined (see TH1::Sumw2), errors are also recalculated

Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this if not already set.

Note also that adding histogram with labels is not supported, histogram will be added merging them by bin number independently of the labels. For adding histogram ith labels one should use TH1::Merge

SPECIAL CASE (Average/Efficiency histograms) For histograms representing averages or efficiencies, one should compute the average of the two histograms and not the sum. One can mark a histogram to be an average histogram by setting its bit kIsAverage with myhist.SetBit(TH1::kIsAverage); Note that the two histograms must have their kIsAverage bit set

IMPORTANT NOTE: If you intend to use the errors of this histogram later you should call Sumw2 before making this operation. This is particularly important if you fit the histogram after TH1::Add

IMPORTANT NOTE2: You should be careful about the statistics of the returned histogram, whose statistics may be binned or unbinned, depending on whether c1 is negative, whether TAxis::kAxisRange is true, and whether TH1::ResetStats has been called on either this or h1. See TH1::GetStats.

ANOTHER SPECIAL CASE : h1 = h2 and c2 < 0 do a scaling this = c1 * h1 / (bin Volume)

The function returns kFALSE if the Add operation failed

Reimplemented in TH2Poly, TProfile, TProfile2D, and TProfile3D.

Definition at line 1080 of file TH1.cxx.

Add() [2/3]

Bool_t TH1::Add ( const TH1 *  h1, Double_t  c1 = 1  )

virtual

Performs the operation: this = this + c1*h1 If errors are defined (see TH1::Sumw2), errors are also recalculated.

Note that if h1 has Sumw2 set, Sumw2 is automatically called for this if not already set.

Note also that adding histogram with labels is not supported, histogram will be added merging them by bin number independently of the labels. For adding histogram with labels one should use TH1::Merge

SPECIAL CASE (Average/Efficiency histograms) For histograms representing averages or efficiencies, one should compute the average of the two histograms and not the sum. One can mark a histogram to be an average histogram by setting its bit kIsAverage with myhist.SetBit(TH1::kIsAverage); Note that the two histograms must have their kIsAverage bit set

IMPORTANT NOTE1: If you intend to use the errors of this histogram later you should call Sumw2 before making this operation. This is particularly important if you fit the histogram after TH1::Add

IMPORTANT NOTE2: if h1 has a normalisation factor, the normalisation factor is used , ie this = this + c1*factor*h1 Use the other TH1::Add function if you do not want this feature

IMPORTANT NOTE3: You should be careful about the statistics of the returned histogram, whose statistics may be binned or unbinned, depending on whether c1 is negative, whether TAxis::kAxisRange is true, and whether TH1::ResetStats has been called on either this or h1. See TH1::GetStats.

The function return kFALSE if the Add operation failed

Reimplemented in TH2Poly, TProfile, TProfile2D, and TProfile3D.

Definition at line 913 of file TH1.cxx.

Add() [3/3]

Bool_t TH1::Add ( TF1 *  f1, Double_t  c1 = 1, Option_t *  option = ""  )

virtual

Performs the operation: this = this + c1*f1 if errors are defined (see TH1::Sumw2), errors are also recalculated.

By default, the function is computed at the centre of the bin. if option "I" is specified (1-d histogram only), the integral of the function in each bin is used instead of the value of the function at the centre of the bin.

Only bins inside the function range are recomputed.

IMPORTANT NOTE: If you intend to use the errors of this histogram later you should call Sumw2 before making this operation. This is particularly important if you fit the histogram after TH1::Add

The function return kFALSE if the Add operation failed

Reimplemented in TH2Poly, TProfile, TProfile2D, and TProfile3D.

Definition at line 822 of file TH1.cxx.

AddBinContent() [1/2]

void TH1::AddBinContent ( Int_t  bin )

virtual

Increment bin content by 1.

Reimplemented in TH1C, TH1S, TH1I, TH1F, TH1D, TH2C, TH2S, TH2I, TH2F, TH2D, TH3C, TH3S, TH3I, TH3F, and TH3D.

Definition at line 1257 of file TH1.cxx.

AddBinContent() [2/2]

void TH1::AddBinContent ( Int_t  bin, Double_t  w  )

virtual

Increment bin content by a weight w.

Reimplemented in TH1C, TH1S, TH1I, TH1F, TH1D, TH2C, TH2S, TH2I, TH2F, TH2D, TH3C, TH3S, TH3I, TH3F, and TH3D.

Definition at line 1265 of file TH1.cxx.

AddDirectory()

void TH1::AddDirectory ( Bool_t  add = kTRUE )

static

Sets the flag controlling the automatic add of histograms in memory.

By default (fAddDirectory = kTRUE), histograms are automatically added to the list of objects in memory. Note that one histogram can be removed from its support directory by calling h->SetDirectory(0) or h->SetDirectory(dir) to add it to the list of objects in the directory dir.

NOTE that this is a static function. To call it, use; TH1::AddDirectory

Definition at line 1282 of file TH1.cxx.

AddDirectoryStatus()

Bool_t TH1::AddDirectoryStatus ( )

static

Static function: cannot be inlined on Windows/NT.

Definition at line 750 of file TH1.cxx.

AndersonDarlingTest() [1/2]

Double_t TH1::AndersonDarlingTest ( const TH1 *  h2, Double_t &  advalue  ) const

virtual

Same function as above but returning also the test statistic value.

Definition at line 7972 of file TH1.cxx.

AndersonDarlingTest() [2/2]

Double_t TH1::AndersonDarlingTest ( const TH1 *  h2, Option_t *  option = ""  ) const

virtual

Statistical test of compatibility in shape between this histogram and h2, using the Anderson-Darling 2 sample test.

The AD 2 sample test formula are derived from the paper F.W Scholz, M.A. Stephens "k-Sample Anderson-Darling Test".

The test is implemented in root in the ROOT::Math::GoFTest class It is the same formula ( (6) in the paper), and also shown in this preprint

Binned data are considered as un-binned data with identical observation happening in the bin center.

Parameters

[in]

option

is a character string to specify options "D" Put out a line of "Debug" printout "T" Return the normalized A-D test statistic

• Note1: Underflow and overflow are not considered in the test
• Note2: The test works only for un-weighted histogram (i.e. representing counts)
• Note3: The histograms are not required to have the same X axis
• Note4: The test works only for 1-dimensional histograms

Definition at line 7954 of file TH1.cxx.

AutoP2FindLimits()

Int_t TH1::AutoP2FindLimits ( Double_t  xmi, Double_t  xma  )

protectedvirtual

Buffer-based estimate of the histogram range using the power of 2 algorithm.

Used by the autobin power of 2 algorithm.

Works on arguments (min and max from fBuffer) and internal inputs: fXmin, fXmax, NBinsX (from fXaxis), ... Result save internally in fXaxis.

Overloaded by TH2 and TH3.

Return -1 if internal inputs are inconsistent, 0 otherwise.

Definition at line 1331 of file TH1.cxx.

AutoP2GetBins()

Int_t TH1::AutoP2GetBins ( Int_t  n )

inlinestaticprotected

Auxiliary function to get the next power of 2 integer value larger then n.

Used by the autobin power of 2 algorithm

Definition at line 1309 of file TH1.cxx.

AutoP2GetPower2()

Double_t TH1::AutoP2GetPower2 ( Double_t  x, Bool_t  next = kTRUE  )

inlinestaticprotected

Auxiliary function to get the power of 2 next (larger) or previous (smaller) a given x.

next = kTRUE : next larger next = kFALSE : previous smaller

Used by the autobin power of 2 algorithm

Definition at line 1296 of file TH1.cxx.

AxisChoice()

Int_t TH1::AxisChoice ( Option_t *  axis ) const

protected

Choose an axis according to "axis".

Definition at line 14 of file Haxis.cxx.

Browse()

void TH1::Browse ( TBrowser *  b )

virtual

Browse the Histogram object.

Reimplemented from TObject.

Definition at line 758 of file TH1.cxx.

BufferEmpty()

Int_t TH1::BufferEmpty ( Int_t  action = 0 )

virtual

Fill histogram with all entries in the buffer.

• action = -1 histogram is reset and refilled from the buffer (called by THistPainter::Paint)
• action = 0 histogram is reset and filled from the buffer. When the histogram is filled from the buffer the value fBuffer[0] is set to a negative number (= - number of entries) When calling with action == 0 the histogram is NOT refilled when fBuffer[0] is < 0 While when calling with action = -1 the histogram is reset and ALWAYS refilled independently if the histogram was filled before. This is needed when drawing the histogram
• action = 1 histogram is filled and buffer is deleted The buffer is automatically deleted when filling the histogram and the entries is larger than the buffer size

Reimplemented in TH2, TH3, TProfile, TProfile2D, and TProfile3D.

Definition at line 1402 of file TH1.cxx.

BufferFill()

Int_t TH1::BufferFill ( Double_t  x, Double_t  w  )

protectedvirtual

accumulate arguments in buffer.

When buffer is full, empty the buffer

• fBuffer[0] = number of entries in buffer
• fBuffer[1] = w of first entry
• fBuffer[2] = x of first entry

Reimplemented in TH2, TH3, TProfile, TProfile2D, and TProfile3D.

Definition at line 1492 of file TH1.cxx.

Build()

void TH1::Build ( )

private

Creates histogram basic data structure.

Definition at line 767 of file TH1.cxx.

CanExtendAllAxes()

Bool_t TH1::CanExtendAllAxes ( ) const

virtual

Returns true if all axes are extendable.

Definition at line 6596 of file TH1.cxx.

CheckAxisLimits()

bool TH1::CheckAxisLimits ( const TAxis *  a1, const TAxis *  a2  )

staticprotected

Check that the axis limits of the histograms are the same.

If a first and last bin is passed the axis is compared between the given range

Definition at line 1588 of file TH1.cxx.

CheckBinLabels()

bool TH1::CheckBinLabels ( const TAxis *  a1, const TAxis *  a2  )

staticprotected

Check that axis have same labels.

Definition at line 1556 of file TH1.cxx.

CheckBinLimits()

bool TH1::CheckBinLimits ( const TAxis *  a1, const TAxis *  a2  )

staticprotected

Check bin limits.

Definition at line 1527 of file TH1.cxx.

CheckConsistency()

bool TH1::CheckConsistency ( const TH1 *  h1, const TH1 *  h2  )

staticprotected

Check histogram compatibility.

Definition at line 1676 of file TH1.cxx.

CheckConsistentSubAxes()

bool TH1::CheckConsistentSubAxes ( const TAxis *  a1, Int_t  firstBin1, Int_t  lastBin1, const TAxis *  a2, Int_t  firstBin2 = 0, Int_t  lastBin2 = 0  )

staticprotected

Check that two sub axis are the same.

The limits are defined by first bin and last bin N.B. no check is done in this case for variable bins

Definition at line 1639 of file TH1.cxx.

CheckEqualAxes()

bool TH1::CheckEqualAxes ( const TAxis *  a1, const TAxis *  a2  )

staticprotected

Check that the axis are the same.

Definition at line 1603 of file TH1.cxx.

Chi2Test()

Double_t TH1::Chi2Test ( const TH1 *  h2, Option_t *  option = "UU", Double_t *  res = 0  ) const

virtual

\( \chi^{2} \) test for comparing weighted and unweighted histograms

Function: Returns p-value. Other return values are specified by the 3rd parameter

Parameters

[in]	h2	the second histogram
[in]	option	"UU" = experiment experiment comparison (unweighted-unweighted) "UW" = experiment MC comparison (unweighted-weighted). Note that the first histogram should be unweighted "WW" = MC MC comparison (weighted-weighted) "NORM" = to be used when one or both of the histograms is scaled but the histogram originally was unweighted by default underflows and overflows are not included: "OF" = overflows included "UF" = underflows included "P" = print chi2, ndf, p_value, igood "CHI2" = returns chi2 instead of p-value "CHI2/NDF" = returns \( \chi^{2} \)/ndf
[in]	res	not empty - computes normalized residuals and returns them in this array

The current implementation is based on the papers \( \chi^{2} \) test for comparison of weighted and unweighted histograms" in Proceedings of PHYSTAT05 and "Comparison weighted and unweighted histograms", arXiv:physics/0605123 by N.Gagunashvili. This function has been implemented by Daniel Haertl in August 2006.

Introduction:

A frequently used technique in data analysis is the comparison of histograms. First suggested by Pearson [1] the \( \chi^{2} \) test of homogeneity is used widely for comparing usual (unweighted) histograms. This paper describes the implementation modified \( \chi^{2} \) tests for comparison of weighted and unweighted histograms and two weighted histograms [2] as well as usual Pearson's \( \chi^{2} \) test for comparison two usual (unweighted) histograms.

Overview:

Comparison of two histograms expect hypotheses that two histograms represent identical distributions. To make a decision p-value should be calculated. The hypotheses of identity is rejected if the p-value is lower then some significance level. Traditionally significance levels 0.1, 0.05 and 0.01 are used. The comparison procedure should include an analysis of the residuals which is often helpful in identifying the bins of histograms responsible for a significant overall \( \chi^{2} \) value. Residuals are the difference between bin contents and expected bin contents. Most convenient for analysis are the normalized residuals. If hypotheses of identity are valid then normalized residuals are approximately independent and identically distributed random variables having N(0,1) distribution. Analysis of residuals expect test of above mentioned properties of residuals. Notice that indirectly the analysis of residuals increase the power of \( \chi^{2} \) test.

Methods of comparison:

\( \chi^{2} \) test for comparison two (unweighted) histograms: Let us consider two histograms with the same binning and the number of bins equal to r. Let us denote the number of events in the ith bin in the first histogram as ni and as mi in the second one. The total number of events in the first histogram is equal to:

\[ N = \sum_{i=1}^{r} n_{i} \]

and

\[ M = \sum_{i=1}^{r} m_{i} \]

in the second histogram. The hypothesis of identity (homogeneity) [3] is that the two histograms represent random values with identical distributions. It is equivalent that there exist r constants p1,...,pr, such that

\[ \sum_{i=1}^{r} p_{i}=1 \]

and the probability of belonging to the ith bin for some measured value in both experiments is equal to pi. The number of events in the ith bin is a random variable with a distribution approximated by a Poisson probability distribution

\[ \frac{e^{-Np_{i}}(Np_{i})^{n_{i}}}{n_{i}!} \]

for the first histogram and with distribution

\[ \frac{e^{-Mp_{i}}(Mp_{i})^{m_{i}}}{m_{i}!} \]

for the second histogram. If the hypothesis of homogeneity is valid, then the maximum likelihood estimator of pi, i=1,...,r, is

\[ \hat{p}_{i}= \frac{n_{i}+m_{i}}{N+M} \]

and then

\[ X^{2} = \sum_{i=1}^{r}\frac{(n_{i}-N\hat{p}_{i})^{2}}{N\hat{p}_{i}} + \sum_{i=1}^{r}\frac{(m_{i}-M\hat{p}_{i})^{2}}{M\hat{p}_{i}} =\frac{1}{MN} \sum_{i=1}^{r}\frac{(Mn_{i}-Nm_{i})^{2}}{n_{i}+m_{i}} \]

has approximately a \( \chi^{2}_{(r-1)} \) distribution [3]. The comparison procedure can include an analysis of the residuals which is often helpful in identifying the bins of histograms responsible for a significant overall \( \chi^{2} \) value. Most convenient for analysis are the adjusted (normalized) residuals [4]

\[ r_{i} = \frac{n_{i}-N\hat{p}_{i}}{\sqrt{N\hat{p}_{i}}\sqrt{(1-N/(N+M))(1-(n_{i}+m_{i})/(N+M))}} \]

If hypotheses of homogeneity are valid then residuals ri are approximately independent and identically distributed random variables having N(0,1) distribution. The application of the \( \chi^{2} \) test has restrictions related to the value of the expected frequencies Npi, Mpi, i=1,...,r. A conservative rule formulated in [5] is that all the expectations must be 1 or greater for both histograms. In practical cases when expected frequencies are not known the estimated expected frequencies \( M\hat{p}_{i}, N\hat{p}_{i}, i=1,...,r \) can be used.

Unweighted and weighted histograms comparison:

A simple modification of the ideas described above can be used for the comparison of the usual (unweighted) and weighted histograms. Let us denote the number of events in the ith bin in the unweighted histogram as ni and the common weight of events in the ith bin of the weighted histogram as wi. The total number of events in the unweighted histogram is equal to

\[ N = \sum_{i=1}^{r} n_{i} \]

and the total weight of events in the weighted histogram is equal to

\[ W = \sum_{i=1}^{r} w_{i} \]

Let us formulate the hypothesis of identity of an unweighted histogram to a weighted histogram so that there exist r constants p1,...,pr, such that

\[ \sum_{i=1}^{r} p_{i} = 1 \]

for the unweighted histogram. The weight wi is a random variable with a distribution approximated by the normal probability distribution \( N(Wp_{i},\sigma_{i}^{2}) \) where \( \sigma_{i}^{2} \) is the variance of the weight wi. If we replace the variance \( \sigma_{i}^{2} \) with estimate \( s_{i}^{2} \) (sum of squares of weights of events in the ith bin) and the hypothesis of identity is valid, then the maximum likelihood estimator of pi,i=1,...,r, is

\[ \hat{p}_{i} = \frac{Ww_{i}-Ns_{i}^{2}+\sqrt{(Ww_{i}-Ns_{i}^{2})^{2}+4W^{2}s_{i}^{2}n_{i}}}{2W^{2}} \]

We may then use the test statistic

\[ X^{2} = \sum_{i=1}^{r} \frac{(n_{i}-N\hat{p}_{i})^{2}}{N\hat{p}_{i}} + \sum_{i=1}^{r} \frac{(w_{i}-W\hat{p}_{i})^{2}}{s_{i}^{2}} \]

and it has approximately a \( \sigma^{2}_{(r-1)} \) distribution [2]. This test, as well as the original one [3], has a restriction on the expected frequencies. The expected frequencies recommended for the weighted histogram is more than 25. The value of the minimal expected frequency can be decreased down to 10 for the case when the weights of the events are close to constant. In the case of a weighted histogram if the number of events is unknown, then we can apply this recommendation for the equivalent number of events as

\[ n_{i}^{equiv} = \frac{ w_{i}^{2} }{ s_{i}^{2} } \]

The minimal expected frequency for an unweighted histogram must be 1. Notice that any usual (unweighted) histogram can be considered as a weighted histogram with events that have constant weights equal to 1. The variance \( z_{i}^{2} \) of the difference between the weight wi and the estimated expectation value of the weight is approximately equal to:

\[ z_{i}^{2} = Var(w_{i}-W\hat{p}_{i}) = N\hat{p}_{i}(1-N\hat{p}_{i})\left(\frac{Ws_{i}^{2}}{\sqrt{(Ns_{i}^{2}-w_{i}W)^{2}+4W^{2}s_{i}^{2}n_{i}}}\right)^{2}+\frac{s_{i}^{2}}{4}\left(1+\frac{Ns_{i}^{2}-w_{i}W}{\sqrt{(Ns_{i}^{2}-w_{i}W)^{2}+4W^{2}s_{i}^{2}n_{i}}}\right)^{2} \]

The residuals

\[ r_{i} = \frac{w_{i}-W\hat{p}_{i}}{z_{i}} \]

have approximately a normal distribution with mean equal to 0 and standard deviation equal to 1.

Two weighted histograms comparison:

Let us denote the common weight of events of the ith bin in the first histogram as w1i and as w2i in the second one. The total weight of events in the first histogram is equal to

\[ W_{1} = \sum_{i=1}^{r} w_{1i} \]

and

\[ W_{2} = \sum_{i=1}^{r} w_{2i} \]

in the second histogram. Let us formulate the hypothesis of identity of weighted histograms so that there exist r constants p1,...,pr, such that

\[ \sum_{i=1}^{r} p_{i} = 1 \]

and also expectation value of weight w1i equal to W1pi and expectation value of weight w2i equal to W2pi. Weights in both the histograms are random variables with distributions which can be approximated by a normal probability distribution \( N(W_{1}p_{i},\sigma_{1i}^{2}) \) for the first histogram and by a distribution \( N(W_{2}p_{i},\sigma_{2i}^{2}) \) for the second. Here \( \sigma_{1i}^{2} \) and \( \sigma_{2i}^{2} \) are the variances of w1i and w2i with estimators \( s_{1i}^{2} \) and \( s_{2i}^{2} \) respectively. If the hypothesis of identity is valid, then the maximum likelihood and Least Square Method estimator of pi,i=1,...,r, is

\[ \hat{p}_{i} = \frac{w_{1i}W_{1}/s_{1i}^{2}+w_{2i}W_{2} /s_{2i}^{2}}{W_{1}^{2}/s_{1i}^{2}+W_{2}^{2}/s_{2i}^{2}} \]

We may then use the test statistic

\[ X^{2} = \sum_{i=1}^{r} \frac{(w_{1i}-W_{1}\hat{p}_{i})^{2}}{s_{1i}^{2}} + \sum_{i=1}^{r} \frac{(w_{2i}-W_{2}\hat{p}_{i})^{2}}{s_{2i}^{2}} = \sum_{i=1}^{r} \frac{(W_{1}w_{2i}-W_{2}w_{1i})^{2}}{W_{1}^{2}s_{2i}^{2}+W_{2}^{2}s_{1i}^{2}} \]

and it has approximately a \( \chi^{2}_{(r-1)} \) distribution [2]. The normalized or studentised residuals [6]

\[ r_{i} = \frac{w_{1i}-W_{1}\hat{p}_{i}}{s_{1i}\sqrt{1 - \frac{1}{(1+W_{2}^{2}s_{1i}^{2}/W_{1}^{2}s_{2i}^{2})}}} \]

have approximately a normal distribution with mean equal to 0 and standard deviation 1. A recommended minimal expected frequency is equal to 10 for the proposed test.

Numerical examples:

The method described herein is now illustrated with an example. We take a distribution

\[ \phi(x) = \frac{2}{(x-10)^{2}+1} + \frac{1}{(x-14)^{2}+1} (1) \]

defined on the interval [4,16]. Events distributed according to the formula (1) are simulated to create the unweighted histogram. Uniformly distributed events are simulated for the weighted histogram with weights calculated by formula (1). Each histogram has the same number of bins: 20. Fig.1 shows the result of comparison of the unweighted histogram with 200 events (minimal expected frequency equal to one) and the weighted histogram with 500 events (minimal expected frequency equal to 25)

///

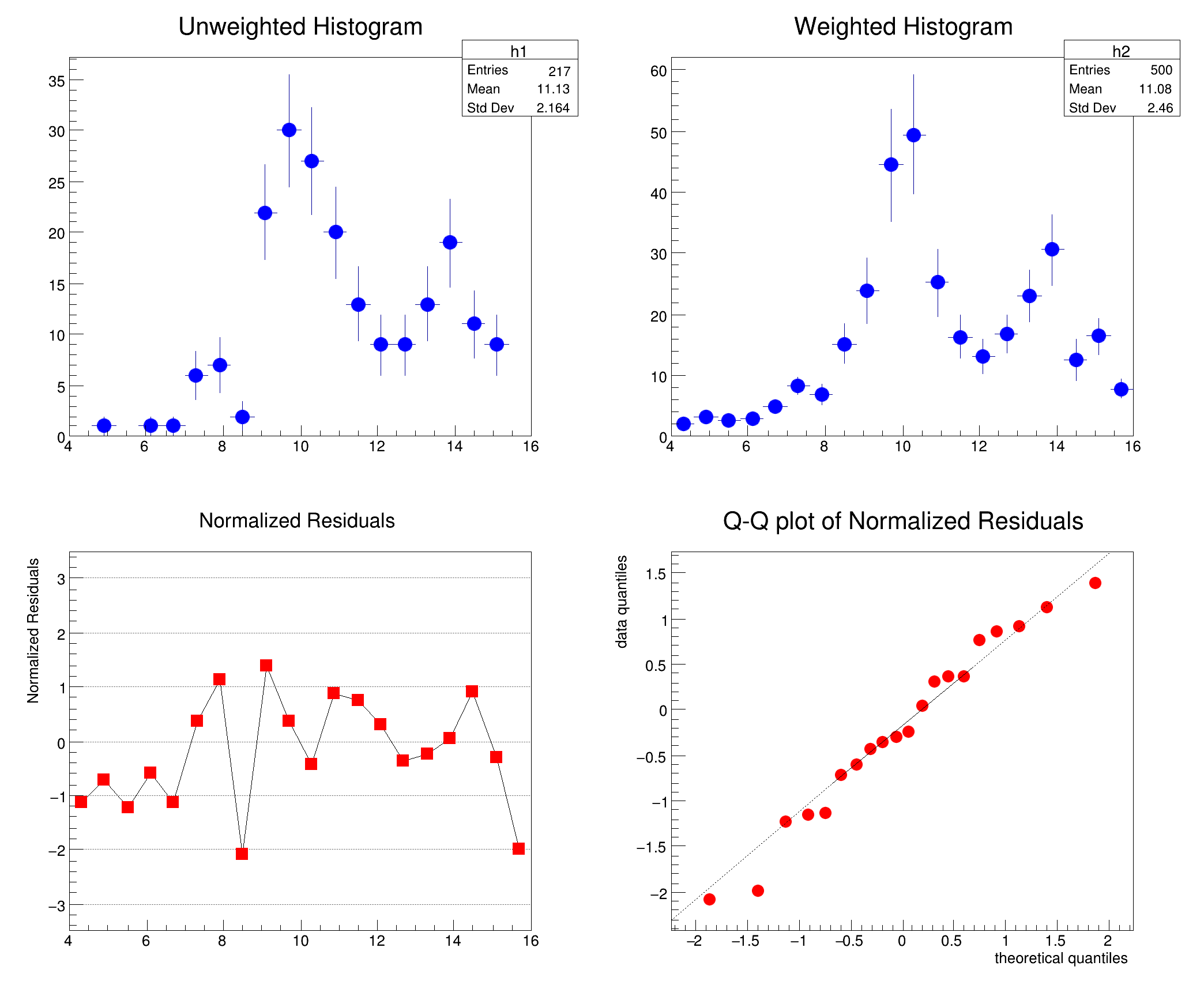
Fig 1. An example of comparison of the unweighted histogram with 200 events and the weighted histogram with 500 events:

1. unweighted histogram;
2. weighted histogram;
3. normalized residuals plot;
4. normal Q-Q plot of residuals.

The value of the test statistic \( \chi^{2} \) is equal to 21.09 with p-value equal to 0.33, therefore the hypothesis of identity of the two histograms can be accepted for 0.05 significant level. The behavior of the normalized residuals plot (see Fig. 1c) and the normal Q-Q plot (see Fig. 1d) of residuals are regular and we cannot identify the outliers or bins with a big influence on \( \chi^{2} \).

The second example presents the same two histograms but 17 events was added to content of bin number 15 in unweighted histogram. Fig.2 shows the result of comparison of the unweighted histogram with 217 events (minimal expected frequency equal to one) and the weighted histogram with 500 events (minimal expected frequency equal to 25)

///

Fig 2. An example of comparison of the unweighted histogram with 217 events and the weighted histogram with 500 events:

1. unweighted histogram;
2. weighted histogram;
3. normalized residuals plot;
4. normal Q-Q plot of residuals.

The value of the test statistic \( \chi^{2} \) is equal to 32.33 with p-value equal to 0.029, therefore the hypothesis of identity of the two histograms is rejected for 0.05 significant level. The behavior of the normalized residuals plot (see Fig. 2c) and the normal Q-Q plot (see Fig. 2d) of residuals are not regular and we can identify the outlier or bin with a big influence on \( \chi^{2} \).

References:

• [1] Pearson, K., 1904. On the Theory of Contingency and Its Relation to Association and Normal Correlation. Drapers' Co. Memoirs, Biometric Series No. 1, London.
• [2] Gagunashvili, N., 2006. \( \sigma^{2} \) test for comparison of weighted and unweighted histograms. Statistical Problems in Particle Physics, Astrophysics and Cosmology, Proceedings of PHYSTAT05, Oxford, UK, 12-15 September 2005, Imperial College Press, London, 43-44. Gagunashvili,N., Comparison of weighted and unweighted histograms, arXiv:physics/0605123, 2006.
• [3] Cramer, H., 1946. Mathematical methods of statistics. Princeton University Press, Princeton.
• [4] Haberman, S.J., 1973. The analysis of residuals in cross-classified tables. Biometrics 29, 205-220.
• [5] Lewontin, R.C. and Felsenstein, J., 1965. The robustness of homogeneity test in 2xN tables. Biometrics 21, 19-33.
• [6] Seber, G.A.F., Lee, A.J., 2003, Linear Regression Analysis. John Wiley & Sons Inc., New York.

Definition at line 2005 of file TH1.cxx.

Chi2TestX()

Double_t TH1::Chi2TestX ( const TH1 *  h2, Double_t &  chi2, Int_t &  ndf, Int_t &  igood, Option_t *  option = "UU", Double_t *  res = 0  ) const

virtual

The computation routine of the Chisquare test.

For the method description, see Chi2Test() function.

Returns

p-value

Parameters

[in]	h2	the second histogram
[in]	option	"UU" = experiment experiment comparison (unweighted-unweighted) "UW" = experiment MC comparison (unweighted-weighted). Note that the first histogram should be unweighted "WW" = MC MC comparison (weighted-weighted) "NORM" = if one or both histograms is scaled "OF" = overflows included "UF" = underflows included by default underflows and overflows are not included
[out]	igood	test output igood=0 - no problems For unweighted unweighted comparison igood=1'There is a bin in the 1st histogram with less than 1 event' igood=2'There is a bin in the 2nd histogram with less than 1 event' igood=3'when the conditions for igood=1 and igood=2 are satisfied' For unweighted weighted comparison igood=1'There is a bin in the 1st histogram with less then 1 event' igood=2'There is a bin in the 2nd histogram with less then 10 effective number of events' igood=3'when the conditions for igood=1 and igood=2 are satisfied' For weighted weighted comparison igood=1'There is a bin in the 1st histogram with less then 10 effective number of events' igood=2'There is a bin in the 2nd histogram with less then 10 effective number of events' igood=3'when the conditions for igood=1 and igood=2 are satisfied'
[out]	chi2	chisquare of the test
[out]	ndf	number of degrees of freedom (important, when both histograms have the same empty bins)
[out]	res	normalized residuals for further analysis

Definition at line 2064 of file TH1.cxx.

Chisquare()

Double_t TH1::Chisquare ( TF1 *  func, Option_t *  option = ""  ) const

virtual

Compute and return the chisquare of this histogram with respect to a function The chisquare is computed by weighting each histogram point by the bin error By default the full range of the histogram is used.

Use option "R" for restricting the chisquare calculation to the given range of the function Use option "L" for using the chisquare based on the poisson likelihood (Baker-Cousins Chisquare)

Definition at line 2492 of file TH1.cxx.

ClearUnderflowAndOverflow()

void TH1::ClearUnderflowAndOverflow ( )

virtual

Remove all the content from the underflow and overflow bins, without changing the number of entries After calling this method, every undeflow and overflow bins will have content 0.0 The Sumw2 is also cleared, since there is no more content in the bins.

Definition at line 2511 of file TH1.cxx.

Clone()

TObject * TH1::Clone ( const char *  newname = 0 ) const

virtual

Make a complete copy of the underlying object.

If 'newname' is set, the copy's name will be set to that name.

Reimplemented from TNamed.

Reimplemented in TH2Poly.

Definition at line 2740 of file TH1.cxx.

ComputeIntegral()

Double_t TH1::ComputeIntegral ( Bool_t  onlyPositive = false )

virtual

Compute integral (cumulative sum of bins) The result stored in fIntegral is used by the GetRandom functions.

This function is automatically called by GetRandom when the fIntegral array does not exist or when the number of entries in the histogram has changed since the previous call to GetRandom. The resulting integral is normalized to 1 If the routine is called with the onlyPositive flag set an error will be produced in case of negative bin content and a NaN value returned

Reimplemented in TH2Poly.

Definition at line 2530 of file TH1.cxx.

Copy()

void TH1::Copy ( TObject &  obj ) const

virtual

Copy this histogram structure to newth1.

Note that this function does not copy the list of associated functions. Use TObject::Clone to make a full copy of an histogram.

Note also that the histogram it will be created in gDirectory (if AddDirectoryStatus()=true) or will not be added to any directory if AddDirectoryStatus()=false independently of the current directory stored in the original histogram

Reimplemented from TNamed.

Reimplemented in TH1C, TH1S, TH1I, TH1F, TH1D, TH2, TH2C, TH2S, TH2I, TH2F, TH2D, TH3, TH3C, TH3S, TH3I, TH3F, TH3D, TProfile, TProfile2D, TProfile3D, and TH1K.

Definition at line 2663 of file TH1.cxx.

DirectoryAutoAdd()

void TH1::DirectoryAutoAdd ( TDirectory *  dir )

virtual

Perform the automatic addition of the histogram to the given directory.

Note this function is called in place when the semantic requires this object to be added to a directory (I.e. when being read from a TKey or being Cloned)

Definition at line 2789 of file TH1.cxx.

DistancetoPrimitive()

Int_t TH1::DistancetoPrimitive ( Int_t  px, Int_t  py  )

virtual

Compute distance from point px,py to a line.

Compute the closest distance of approach from point px,py to elements of an histogram. The distance is computed in pixels units.

Algorithm:

Currently, this simple model computes the distance from the mouse to the histogram contour only.

Reimplemented from TObject.

Reimplemented in TGLTH3Composition.

Definition at line 2811 of file TH1.cxx.

Divide() [1/3]

Bool_t TH1::Divide ( const TH1 *  h1 )

virtual

Divide this histogram by h1.

this = this/h1 if errors are defined (see TH1::Sumw2), errors are also recalculated. Note that if h1 has Sumw2 set, Sumw2 is automatically called for this if not already set. The resulting errors are calculated assuming uncorrelated histograms. See the other TH1::Divide that gives the possibility to optionally compute binomial errors.

IMPORTANT NOTE: If you intend to use the errors of this histogram later you should call Sumw2 before making this operation. This is particularly important if you fit the histogram after TH1::Scale

The function return kFALSE if the divide operation failed

Reimplemented in TProfile, TProfile2D, and TProfile3D.

Definition at line 2896 of file TH1.cxx.

Divide() [2/3]

Bool_t TH1::Divide ( const TH1 *  h1, const TH1 *  h2, Double_t  c1 = 1, Double_t  c2 = 1, Option_t *  option = ""  )

virtual

Replace contents of this histogram by the division of h1 by h2.

this = c1*h1/(c2*h2)

If errors are defined (see TH1::Sumw2), errors are also recalculated Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this if not already set. The resulting errors are calculated assuming uncorrelated histograms. However, if option ="B" is specified, Binomial errors are computed. In this case c1 and c2 do not make real sense and they are ignored.

IMPORTANT NOTE: If you intend to use the errors of this histogram later you should call Sumw2 before making this operation. This is particularly important if you fit the histogram after TH1::Divide

Please note also that in the binomial case errors are calculated using standard binomial statistics, which means when b1 = b2, the error is zero. If you prefer to have efficiency errors not going to zero when the efficiency is 1, you must use the function TGraphAsymmErrors::BayesDivide, which will return an asymmetric and non-zero lower error for the case b1=b2.

The function return kFALSE if the divide operation failed

Reimplemented in TProfile, TProfile2D, and TProfile3D.

Definition at line 2963 of file TH1.cxx.

Divide() [3/3]

Bool_t TH1::Divide ( TF1 *  f1, Double_t  c1 = 1  )

virtual

Performs the operation: this = this/(c1*f1) if errors are defined (see TH1::Sumw2), errors are also recalculated.

Only bins inside the function range are recomputed. IMPORTANT NOTE: If you intend to use the errors of this histogram later you should call Sumw2 before making this operation. This is particularly important if you fit the histogram after TH1::Divide

The function return kFALSE if the divide operation failed

Reimplemented in TH2Poly, TProfile, TProfile2D, and TProfile3D.

Definition at line 2828 of file TH1.cxx.

DoFillN()

void TH1::DoFillN ( Int_t  ntimes, const Double_t *  x, const Double_t *  w, Int_t  stride = 1  )

protectedvirtual

Internal method to fill histogram content from a vector called directly by TH1::BufferEmpty.

Definition at line 3479 of file TH1.cxx.

DoIntegral()

Double_t TH1::DoIntegral ( Int_t  ix1, Int_t  ix2, Int_t  iy1, Int_t  iy2, Int_t  iz1, Int_t  iz2, Double_t &  err, Option_t *  opt, Bool_t  doerr = kFALSE  ) const

protectedvirtual

Internal function compute integral and optionally the error between the limits specified by the bin number values working for all histograms (1D, 2D and 3D)

Definition at line 7870 of file TH1.cxx.

Draw()

void TH1::Draw ( Option_t *  option = "" )

virtual

Draw this histogram with options.

Histograms are drawn via the THistPainter class. Each histogram has a pointer to its own painter (to be usable in a multithreaded program). The same histogram can be drawn with different options in different pads. When an histogram drawn in a pad is deleted, the histogram is automatically removed from the pad or pads where it was drawn. If an histogram is drawn in a pad, then filled again, the new status of the histogram will be automatically shown in the pad next time the pad is updated. One does not need to redraw the histogram. To draw the current version of an histogram in a pad, one can use h->DrawCopy(); This makes a clone of the histogram. Once the clone is drawn, the original histogram may be modified or deleted without affecting the aspect of the clone. By default, TH1::Draw clears the current pad.

One can use TH1::SetMaximum and TH1::SetMinimum to force a particular value for the maximum or the minimum scale on the plot.

TH1::UseCurrentStyle can be used to change all histogram graphics attributes to correspond to the current selected style. This function must be called for each histogram. In case one reads and draws many histograms from a file, one can force the histograms to inherit automatically the current graphics style by calling before gROOT->ForceStyle();

See the THistPainter class for a description of all the drawing options.

Reimplemented from TObject.

Definition at line 3073 of file TH1.cxx.

DrawCopy()

TH1 * TH1::DrawCopy ( Option_t *  option = "", const char *  name_postfix = "_copy"  ) const

virtual

Copy this histogram and Draw in the current pad.

Once the histogram is drawn into the pad, any further modification using graphics input will be made on the copy of the histogram, and not to the original object. By default a postfix "_copy" is added to the histogram name. Pass an empty postfix in case you want to draw an histogram with the same name

See Draw for the list of options

Definition at line 3120 of file TH1.cxx.

DrawNormalized()

TH1 * TH1::DrawNormalized ( Option_t *  option = "", Double_t  norm = 1  ) const

virtual

Draw a normalized copy of this histogram.

A clone of this histogram is normalized to norm and drawn with option. A pointer to the normalized histogram is returned. The contents of the histogram copy are scaled such that the new sum of weights (excluding under and overflow) is equal to norm. Note that the returned normalized histogram is not added to the list of histograms in the current directory in memory. It is the user's responsibility to delete this histogram. The kCanDelete bit is set for the returned object. If a pad containing this copy is cleared, the histogram will be automatically deleted.

See Draw for the list of options

Definition at line 3150 of file TH1.cxx.

DrawPanel()

void TH1::DrawPanel ( )

virtual

Display a panel with all histogram drawing options.

See class TDrawPanelHist for example

Definition at line 3181 of file TH1.cxx.

Eval()

void TH1::Eval ( TF1 *  f1, Option_t *  option = ""  )

virtual

Evaluate function f1 at the center of bins of this histogram.

• If option "R" is specified, the function is evaluated only for the bins included in the function range.
• If option "A" is specified, the value of the function is added to the existing bin contents
• If option "S" is specified, the value of the function is used to generate a value, distributed according to the Poisson distribution, with f1 as the mean.

Definition at line 3198 of file TH1.cxx.

ExecuteEvent()

void TH1::ExecuteEvent ( Int_t  event, Int_t  px, Int_t  py  )

virtual

Execute action corresponding to one event.

This member function is called when a histogram is clicked with the locator

If Left button clicked on the bin top value, then the content of this bin is modified according to the new position of the mouse when it is released.

Reimplemented from TObject.

Reimplemented in TGLTH3Composition.

Definition at line 3246 of file TH1.cxx.

ExtendAxis()

void TH1::ExtendAxis ( Double_t  x, TAxis *  axis  )

virtual

Histogram is resized along axis such that x is in the axis range.

The new axis limits are recomputed by doubling iteratively the current axis range until the specified value x is within the limits. The algorithm makes a copy of the histogram, then loops on all bins of the old histogram to fill the extended histogram. Takes into account errors (Sumw2) if any. The algorithm works for 1-d, 2-D and 3-D histograms. The axis must be extendable before invoking this function. Ex:

h->GetXaxis()->SetCanExtend(kTRUE);

Reimplemented in TProfile, TProfile2D, and TProfile3D.

Definition at line 6464 of file TH1.cxx.

FFT()

TH1 * TH1::FFT ( TH1 *  h_output, Option_t *  option  )

virtual

This function allows to do discrete Fourier transforms of TH1 and TH2.

Available transform types and flags are described below.

To extract more information about the transform, use the function TVirtualFFT::GetCurrentTransform() to get a pointer to the current transform object.

Parameters

[out]	h_output	histogram for the output. If a null pointer is passed, a new histogram is created and returned, otherwise, the provided histogram is used and should be big enough
[in]	option	option parameters consists of 3 parts: option on what to return "RE" - returns a histogram of the real part of the output "IM" - returns a histogram of the imaginary part of the output "MAG"- returns a histogram of the magnitude of the output "PH" - returns a histogram of the phase of the output option of transform type "R2C" - real to complex transforms - default "R2HC" - real to halfcomplex (special format of storing output data, results the same as for R2C) "DHT" - discrete Hartley transform real to real transforms (sine and cosine): "R2R_0", "R2R_1", "R2R_2", "R2R_3" - discrete cosine transforms of types I-IV "R2R_4", "R2R_5", "R2R_6", "R2R_7" - discrete sine transforms of types I-IV To specify the type of each dimension of a 2-dimensional real to real transform, use options of form "R2R_XX", for example, "R2R_02" for a transform, which is of type "R2R_0" in 1st dimension and "R2R_2" in the 2nd. option of transform flag "ES" (from "estimate") - no time in preparing the transform, but probably sub-optimal performance "M" (from "measure") - some time spend in finding the optimal way to do the transform "P" (from "patient") - more time spend in finding the optimal way to do the transform "EX" (from "exhaustive") - the most optimal way is found This option should be chosen depending on how many transforms of the same size and type are going to be done. Planning is only done once, for the first transform of this size and type. Default is "ES".

Examples of valid options: "Mag R2C M" "Re R2R_11" "Im R2C ES" "PH R2HC EX"

Reimplemented in TH2Poly.

Definition at line 3290 of file TH1.cxx.

Fill() [1/3]

Int_t TH1::Fill ( const char *  namex, Double_t  w  )

virtual

Increment bin with namex with a weight w.

if x is less than the low-edge of the first bin, the Underflow bin is incremented if x is equal to or greater than the upper edge of last bin, the Overflow bin is incremented

If the weight is not equal to 1, the storage of the sum of squares of weights is automatically triggered and the sum of the squares of weights is incremented by \( w^2 \) in the bin corresponding to x.

The function returns the corresponding bin number which has its content incremented by w.

Reimplemented in TH2, TH3, TProfile2D, TProfile3D, TH1K, TH2Poly, TProfile2Poly, and TProfile.

Definition at line 3418 of file TH1.cxx.

Fill() [2/3]

Int_t TH1::Fill ( Double_t  x )

virtual

Increment bin with abscissa X by 1.

if x is less than the low-edge of the first bin, the Underflow bin is incremented if x is equal to or greater than the upper edge of last bin, the Overflow bin is incremented

If the storage of the sum of squares of weights has been triggered, via the function Sumw2, then the sum of the squares of weights is incremented by 1 in the bin corresponding to x.

The function returns the corresponding bin number which has its content incremented by 1

Reimplemented in TH1K, TH2, TH2Poly, TH3, TProfile, TProfile2D, TProfile2Poly, and TProfile3D.

Definition at line 3350 of file TH1.cxx.

Fill() [3/3]

Int_t TH1::Fill ( Double_t  x, Double_t  w  )

virtual

Increment bin with abscissa X with a weight w.

if x is less than the low-edge of the first bin, the Underflow bin is incremented if x is equal to or greater than the upper edge of last bin, the Overflow bin is incremented

If the weight is not equal to 1, the storage of the sum of squares of weights is automatically triggered and the sum of the squares of weights is incremented by \( w^2 \) in the bin corresponding to x.

The function returns the corresponding bin number which has its content incremented by w

Reimplemented in TH1K, TH2, TH2Poly, TProfile, TProfile2D, TProfile2Poly, TH3, TProfile2D, and TProfile3D.

Definition at line 3382 of file TH1.cxx.

FillN() [1/2]

void TH1::FillN ( Int_t  ntimes, const Double_t *  x, const Double_t *  w, Int_t  stride = 1  )

virtual

Fill this histogram with an array x and weights w.

Parameters

[in]	ntimes	number of entries in arrays x and w (array size must be ntimes*stride)
[in]	x	array of values to be histogrammed
[in]	w	array of weighs
[in]	stride	step size through arrays x and w

If the weight is not equal to 1, the storage of the sum of squares of weights is automatically triggered and the sum of the squares of weights is incremented by \( w^2 \) in the bin corresponding to x. if w is NULL each entry is assumed a weight=1

Reimplemented in TH2, TH2Poly, and TProfile.

Definition at line 3453 of file TH1.cxx.

FillN() [2/2]

virtual void TH1::FillN ( Int_t  , const Double_t *  , const Double_t *  , const Double_t *  , Int_t    )

inlinevirtual

Reimplemented in TH2, TH2Poly, and TProfile.

Definition at line 223 of file TH1.h.

FillRandom() [1/2]

void TH1::FillRandom ( const char *  fname, Int_t  ntimes = 5000, TRandom *  rng = nullptr  )

virtual

Fill histogram following distribution in function fname.

Parameters

fname	: Function name used for filling the histogram
ntimes	: number of times the histogram is filled
rng	: (optional) Random number generator used to sample

The distribution contained in the function fname (TF1) is integrated over the channel contents for the bin range of this histogram. It is normalized to 1.

Getting one random number implies:

• Generating a random number between 0 and 1 (say r1)
• Look in which bin in the normalized integral r1 corresponds to
• Fill histogram channel ntimes random numbers are generated

One can also call TF1::GetRandom to get a random variate from a function.

Reimplemented in TH2, and TH3.

Definition at line 3525 of file TH1.cxx.

FillRandom() [2/2]

void TH1::FillRandom ( TH1 *  h, Int_t  ntimes = 5000, TRandom *  rng = nullptr  )

virtual

Fill histogram following distribution in histogram h.

Parameters

h	: Histogram pointer used for sampling random number
ntimes	: number of times the histogram is filled
rng	: (optional) Random number generator used for sampling

The distribution contained in the histogram h (TH1) is integrated over the channel contents for the bin range of this histogram. It is normalized to 1.

Getting one random number implies:

• Generating a random number between 0 and 1 (say r1)
• Look in which bin in the normalized integral r1 corresponds to
• Fill histogram channel ntimes random numbers are generated

SPECIAL CASE when the target histogram has the same binning as the source. in this case we simply use a poisson distribution where the mean value per bin = bincontent/integral.

Reimplemented in TH2, and TH3.

Definition at line 3596 of file TH1.cxx.

FindBin()

Int_t TH1::FindBin ( Double_t  x, Double_t  y = 0, Double_t  z = 0  )

virtual

Return Global bin number corresponding to x,y,z.

2-D and 3-D histograms are represented with a one dimensional structure. This has the advantage that all existing functions, such as GetBinContent, GetBinError, GetBinFunction work for all dimensions. This function tries to extend the axis if the given point belongs to an under-/overflow bin AND if CanExtendAllAxes() is true.

See also TH1::GetBin, TAxis::FindBin and TAxis::FindFixBin

Reimplemented in TH2Poly.

Definition at line 3680 of file TH1.cxx.

FindFirstBinAbove()

Int_t TH1::FindFirstBinAbove ( Double_t  threshold = 0, Int_t  axis = 1, Int_t  firstBin = 1, Int_t  lastBin = -1  ) const

virtual

Find first bin with content > threshold for axis (1=x, 2=y, 3=z) if no bins with content > threshold is found the function returns -1.

The search will occur between the specified first and last bin. Specifying the value of the last bin to search to less than zero will search until the last defined bin.

Definition at line 3742 of file TH1.cxx.

FindFixBin()

Int_t TH1::FindFixBin ( Double_t  x, Double_t  y = 0, Double_t  z = 0  ) const

virtual

Return Global bin number corresponding to x,y,z.

2-D and 3-D histograms are represented with a one dimensional structure. This has the advantage that all existing functions, such as GetBinContent, GetBinError, GetBinFunction work for all dimensions. This function DOES NOT try to extend the axis if the given point belongs to an under-/overflow bin.

See also TH1::GetBin, TAxis::FindBin and TAxis::FindFixBin

Definition at line 3713 of file TH1.cxx.

FindLastBinAbove()

Int_t TH1::FindLastBinAbove ( Double_t  threshold = 0, Int_t  axis = 1, Int_t  firstBin = 1, Int_t  lastBin = -1  ) const

virtual

Find last bin with content > threshold for axis (1=x, 2=y, 3=z) if no bins with content > threshold is found the function returns -1.

The search will occur between the specified first and last bin. Specifying the value of the last bin to search to less than zero will search until the last defined bin.

Definition at line 3805 of file TH1.cxx.

FindNewAxisLimits()

Bool_t TH1::FindNewAxisLimits ( const TAxis *  axis, const Double_t  point, Double_t &  newMin, Double_t &  newMax  )

protectedvirtual

finds new limits for the axis so that point is within the range and the limits are compatible with the previous ones (see TH1::Merge).

new limits are put into newMin and newMax variables. axis - axis whose limits are to be recomputed point - point that should fit within the new axis limits newMin - new minimum will be stored here newMax - new maximum will be stored here. false if failed (e.g. if the initial axis limits are wrong or the new range is more than \( 2^{64} \) times the old one).

Definition at line 6407 of file TH1.cxx.

FindObject() [1/2]

TObject * TH1::FindObject ( const char *  name ) const

virtual

Search object named name in the list of functions.

Reimplemented from TObject.

Definition at line 3865 of file TH1.cxx.

FindObject() [2/2]

TObject * TH1::FindObject ( const TObject *  obj ) const

virtual

Search object obj in the list of functions.

Reimplemented from TObject.

Definition at line 3874 of file TH1.cxx.

Fit() [1/2]

TFitResultPtr TH1::Fit ( const char *  fname, Option_t *  option = "", Option_t *  goption = "", Double_t  xxmin = 0, Double_t  xxmax = 0  )

virtual

Fit histogram with function fname.

fname is the name of an already predefined function created by TF1 or TF2 Predefined functions such as gaus, expo and poln are automatically created by ROOT. fname can also be a formula, accepted by the linear fitter (linear parts divided by "++" sign), for example "x++sin(x)" for fitting "[0]*x+[1]*sin(x)"

This function finds a pointer to the TF1 object with name fname and calls TH1::Fit(TF1 *f1,...)

Definition at line 3892 of file TH1.cxx.

Fit() [2/2]

TFitResultPtr TH1::Fit ( TF1 *  f1, Option_t *  option = "", Option_t *  goption = "", Double_t  xxmin = 0, Double_t  xxmax = 0  )

virtual

Fit histogram with function f1.

Parameters

[in]	option	fit options is given in parameter option. "W" Ignore the bin uncertainties when fitting using the default least square (chi2) method but skip empty bins "WW" Ignore the bin uncertainties when fitting using the default least square (chi2) method and include also the empty bins "I" Use integral of function in bin, normalized by the bin volume, instead of value at bin center "L" Use Loglikelihood method (default is chisquare method) "WL" Use Loglikelihood method and bin contents are not integer, i.e. histogram is weighted (must have Sumw2() set) -"MULTI" Use Loglikelihood method based on multi-nomial distribution. In this case function must be normalized and one fits only the function shape (a not extended binned likelihood fit) "P" Use Pearson chi2 (using expected errors instead of observed errors) "U" Use a User specified fitting algorithm (via SetFCN) "Q" Quiet mode (minimum printing) "V" Verbose mode (default is between Q and V) "E" Perform better Errors estimation using Minos technique "B" User defined parameter settings are used for predefined functions like "gaus", "expo", "poln", "landau". Use this option when you want to fix one or more parameters for these functions. "M" More. Improve fit results. It uses the IMPROVE command of TMinuit (see TMinuit::mnimpr). This algorithm attempts to improve the found local minimum by searching for a better one. "R" Use the Range specified in the function range "N" Do not store the graphics function, do not draw "0" Do not plot the result of the fit. By default the fitted function is drawn unless the option"N" above is specified. "+" Add this new fitted function to the list of fitted functions (by default, any previous function is deleted) "C" In case of linear fitting, don't calculate the chisquare (saves time) "F" If fitting a polN, switch to minuit fitter "S" The result of the fit is returned in the TFitResultPtr (see below Access to the Fit Result)
[in]	goption	specify a list of graphics options. See TH1::Draw for a complete list of these options.
[in]	xxmin	range
[in]	xxmax	range

In order to use the Range option, one must first create a function with the expression to be fitted. For example, if your histogram has a defined range between -4 and 4 and you want to fit a gaussian only in the interval 1 to 3, you can do:

TF1 *f1 = new TF1("f1", "gaus", 1, 3);
histo->Fit("f1", "R");

Setting initial conditions

Parameters must be initialized before invoking the Fit function. The setting of the parameter initial values is automatic for the predefined functions : poln, expo, gaus, landau. One can however disable this automatic computation by specifying the option "B". Note that if a predefined function is defined with an argument, eg, gaus(0), expo(1), you must specify the initial values for the parameters. You can specify boundary limits for some or all parameters via

f1->SetParLimits(p_number, parmin, parmax);

if parmin>=parmax, the parameter is fixed Note that you are not forced to fix the limits for all parameters. For example, if you fit a function with 6 parameters, you can do:

func->SetParameters(0, 3.1, 1.e-6, -8, 0, 100);
func->SetParLimits(3, -10, -4);
func->FixParameter(4, 0);
func->SetParLimits(5, 1, 1);

With this setup, parameters 0->2 can vary freely Parameter 3 has boundaries [-10,-4] with initial value -8 Parameter 4 is fixed to 0 Parameter 5 is fixed to 100. When the lower limit and upper limit are equal, the parameter is fixed. However to fix a parameter to 0, one must call the FixParameter function.

Changing the fitting objective function

By default a chi square function is used for fitting. When option "L" (or "LL") is used a Poisson likelihood function (see note below) is used. Using option "MULTI" a multinomial likelihood fit is used. In this case the function normalization is not fitted but only the function shape. Therefore the provided function must be normalized. The functions are defined in the header Fit/Chi2Func.h or Fit/PoissonLikelihoodFCN and they are implemented using the routines FitUtil::EvaluateChi2 or FitUtil::EvaluatePoissonLogL in the file math/mathcore/src/FitUtil.cxx. To specify a User defined fitting function, specify option "U" and call the following functions:

TVirtualFitter::Fitter(myhist)->SetFCN(MyFittingFunction)

where MyFittingFunction is of type:

extern void MyFittingFunction(Int_t &npar, Double_t *gin, Double_t &f, Double_t *u, Int_t flag);

Chi2 Fits

By default a chi2 (least-square) fit is performed on the histogram. The so-called modified least-square method is used where the residual for each bin is computed using as error the observed value (the bin error)

\[ Chi2 = \sum{ \left(\frac{y(i) - f(x(i) | p )}{e(i)} \right)^2 } \]

where y(i) is the bin content for each bin i, x(i) is the bin center and e(i) is the bin error (sqrt(y(i) for an un-weighted histogram. Bins with zero errors are excluded from the fit. See also later the note on the treatment of empty bins. When using option "I" the residual is computed not using the function value at the bin center, f (x(i) | p), but the integral of the function in the bin, Integral{ f(x|p)dx } divided by the bin volume

Likelihood Fits

When using option "L" a likelihood fit is used instead of the default chi2 square fit. The likelihood is built assuming a Poisson probability density function for each bin. The negative log-likelihood to be minimized is

\[ NLL = \sum{ log Poisson ( y(i) | f(x(i) | p ) ) } \]

The exact likelihood used is the Poisson likelihood described in this paper: S. Baker and R. D. Cousins, “Clarification of the use of chi-square and likelihood functions in fits to histograms,” Nucl. Instrum. Meth. 221 (1984) 437.

This method can then be used only when the bin content represents counts (i.e. errors are sqrt(N) ). The likelihood method has the advantage of treating correctly bins with low statistics. In case of high statistics/bin the distribution of the bin content becomes a normal distribution and the likelihood and chi2 fit give the same result.

The likelihood method, although a bit slower, it is therefore the recommended method in case of low bin statistics, where the chi2 method may give incorrect results, in particular when there are several empty bins (see also below). In case of a weighted histogram, it is possible to perform a likelihood fit by using the option "WL". Note a weighted histogram is an histogram which has been filled with weights and it contains the sum of the weight square ( TH1::Sumw2() has been called). The bin error for a weighted histogram is the square root of the sum of the weight square.

Treatment of Empty Bins

Empty bins, which have the content equal to zero AND error equal to zero, are excluded by default from the chisquare fit, but they are considered in the likelihood fit. since they affect the likelihood if the function value in these bins is not negligible. When using option "WW" these bins will be considered in the chi2 fit with an error of 1. Note that if the histogram is having bins with zero content and non zero-errors they are considered as any other bins in the fit. Instead bins with zero error and non-zero content are excluded in the chi2 fit. A likelihood fit should also not be performed on such an histogram, since we are assuming a wrong pdf for each bin. In general, one should not fit an histogram with non-empty bins and zero errors, apart if all the bins have zero errors. In this case one could use the option "w", which gives a weight=1 for each bin (unweighted least-square fit). Note that in case of histogram with no errors (chi2 fit with option W or W1) the resulting fitted parameter errors are corrected by the obtained chi2 value using this expression: errorp *= sqrt(chisquare/(ndf-1))

Fitting a histogram of dimension N with a function of dimension N-1

It is possible to fit a TH2 with a TF1 or a TH3 with a TF2. In this case the option "Integral" is not allowed and each cell has equal weight. Also in this case the obtained parameter error are corrected as in the case when the option "W" is used (see above)

Associated functions

One or more object (typically a TF1*) can be added to the list of functions (fFunctions) associated to each histogram. When TH1::Fit is invoked, the fitted function is added to this list. Given an histogram h, one can retrieve an associated function with:

TF1 *myfunc = h->GetFunction("myfunc");

Access to the fit result

The function returns a TFitResultPtr which can hold a pointer to a TFitResult object. By default the TFitResultPtr contains only the status of the fit which is return by an automatic conversion of the TFitResultPtr to an integer. One can write in this case directly:

Int_t fitStatus =  h->Fit(myFunc)

If the option "S" is instead used, TFitResultPtr contains the TFitResult and behaves as a smart pointer to it. For example one can do:

TFitResultPtr r = h->Fit(myFunc,"S");
TMatrixDSym cov = r->GetCovarianceMatrix();  //  to access the covariance matrix
Double_t chi2   = r->Chi2(); // to retrieve the fit chi2
Double_t par0   = r->Parameter(0); // retrieve the value for the parameter 0
Double_t err0   = r->ParError(0); // retrieve the error for the parameter 0
r->Print("V");     // print full information of fit including covariance matrix
r->Write();        // store the result in a file

The fit parameters, error and chi2 (but not covariance matrix) can be retrieved also from the fitted function. If the histogram is made persistent, the list of associated functions is also persistent. Given a pointer (see above) to an associated function myfunc, one can retrieve the function/fit parameters with calls such as:

Double_t chi2 = myfunc->GetChisquare();
Double_t par0 = myfunc->GetParameter(0); //value of 1st parameter
Double_t err0 = myfunc->GetParError(0);  //error on first parameter

Access to the fit status

The status of the fit can be obtained converting the TFitResultPtr to an integer independently if the fit option "S" is used or not:

TFitResultPtr r = h->Fit(myFunc,opt);
Int_t fitStatus = r;

The fitStatus is 0 if the fit is OK (i.e no error occurred). The value of the fit status code is negative in case of an error not connected with the minimization procedure, for example when a wrong function is used. Otherwise the return value is the one returned from the minimization procedure. When TMinuit (default case) or Minuit2 are used as minimizer the status returned is : fitStatus = migradResult + 10*minosResult + 100*hesseResult + 1000*improveResult. TMinuit will return 0 (for migrad, minos, hesse or improve) in case of success and 4 in case of error (see the documentation of TMinuit::mnexcm). So for example, for an error only in Minos but not in Migrad a fitStatus of 40 will be returned. Minuit2 will return also 0 in case of success and different values in migrad minos or hesse depending on the error. See in this case the documentation of Minuit2Minimizer::Minimize for the migradResult, Minuit2Minimizer::GetMinosError for the minosResult and Minuit2Minimizer::Hesse for the hesseResult. If other minimizers are used see their specific documentation for the status code returned. For example in the case of Fumili, for the status returned see TFumili::Minimize.

Excluding points

Use TF1::RejectPoint inside your fitting function to exclude points within a certain range from the fit. Example:

Double_t fline(Double_t *x, Double_t *par)
{
   if (x[0] > 2.5 && x[0] < 3.5) {
      TF1::RejectPoint();
      return 0;
   }
   return par[0] + par[1]*x[0];
}
 
void exclude() {
   TF1 *f1 = new TF1("f1", "[0] +[1]*x +gaus(2)", 0, 5);
   f1->SetParameters(6, -1,5, 3, 0.2);
   TH1F *h = new TH1F("h", "background + signal", 100, 0, 5);
   h->FillRandom("f1", 2000);
   TF1 *fline = new TF1("fline", fline, 0, 5, 2);
   fline->SetParameters(2, -1);
   h->Fit("fline", "l");
}

Warning when using the option "0"

When selecting the option "0", the fitted function is added to the list of functions of the histogram, but it is not drawn. You can undo what you disabled in the following way:

h.Fit("myFunction", "0"); // fit, store function but do not draw
h.Draw(); function is not drawn
const Int_t kNotDraw = 1<<9;
h.GetFunction("myFunction")->ResetBit(kNotDraw);
h.Draw();  // function is visible again

Access to the Minimizer information during fitting

This function calls, the ROOT::Fit::FitObject function implemented in HFitImpl.cxx which uses the ROOT::Fit::Fitter class. The Fitter class creates the objective function (e.g. chi2 or likelihood) and uses an implementation of the Minimizer interface for minimizing the function. The default minimizer is Minuit (class TMinuitMinimizer which calls TMinuit). The default can be set in the resource file in etc/system.rootrc. For example

Root.Fitter:      Minuit2

A different fitter can also be set via ROOT::Math::MinimizerOptions::SetDefaultMinimizer (or TVirtualFitter::SetDefaultFitter). For example ROOT::Math::MinimizerOptions::SetDefaultMinimizer("GSLMultiMin","BFGS"); will set the usage of the BFGS algorithm of the GSL multi-dimensional minimization (implemented in libMathMore). ROOT::Math::MinimizerOptions can be used also to set other default options, like maximum number of function calls, minimization tolerance or print level. See the documentation of this class.

For fitting linear functions (containing the "++" sign" and polN functions, the linear fitter is automatically initialized.

Definition at line 4225 of file TH1.cxx.

FitOptionsMake()

Int_t TH1::FitOptionsMake ( Option_t *  option, Foption_t &  Foption  )

static

Decode string choptin and fill fitOption structure.

Definition at line 4584 of file TH1.cxx.

FitPanel()

void TH1::FitPanel ( )

virtual

Display a panel with all histogram fit options.

See class TFitPanel for example

Definition at line 4247 of file TH1.cxx.

GetAsymmetry()

TH1 * TH1::GetAsymmetry	(	TH1 *	h2,
		Double_t	c2 = 1,
		Double_t	dc2 = 0
	)

Return an histogram containing the asymmetry of this histogram with h2, where the asymmetry is defined as:

Asymmetry = (h1 - h2)/(h1 + h2)  where h1 = this

works for 1D, 2D, etc. histograms c2 is an optional argument that gives a relative weight between the two histograms, and dc2 is the error on this weight. This is useful, for example, when forming an asymmetry between two histograms from 2 different data sets that need to be normalized to each other in some way. The function calculates the errors assuming Poisson statistics on h1 and h2 (that is, dh = sqrt(h)).

example: assuming 'h1' and 'h2' are already filled

h3 = h1->GetAsymmetry(h2)

then 'h3' is created and filled with the asymmetry between 'h1' and 'h2'; h1 and h2 are left intact.

Note that it is the user's responsibility to manage the created histogram. The name of the returned histogram will be Asymmetry_nameOfh1-nameOfh2

code proposed by Jason Seely (seely.nosp@m.@mit.nosp@m..edu) and adapted by R.Brun

clone the histograms so top and bottom will have the correct dimensions: Sumw2 just makes sure the errors will be computed properly when we form sums and ratios below.

Definition at line 4302 of file TH1.cxx.

GetAxisColor()

Color_t TH1::GetAxisColor ( Option_t *  axis = "X" ) const

virtual

Return the number of divisions for "axis".

Definition at line 40 of file Haxis.cxx.

GetAxisLabelStatus()

UInt_t TH1::GetAxisLabelStatus ( ) const

protected

Internal function used in TH1::Fill to see which axis is full alphanumeric i.e.

can be extended and is alphanumeric

Definition at line 6635 of file TH1.cxx.

GetBarOffset()

virtual Float_t TH1::GetBarOffset ( ) const

inlinevirtual

Definition at line 255 of file TH1.h.

GetBarWidth()

virtual Float_t TH1::GetBarWidth ( ) const

inlinevirtual

Definition at line 256 of file TH1.h.

GetBin()

Int_t TH1::GetBin ( Int_t  binx, Int_t  biny = 0, Int_t  binz = 0  ) const

virtual

Return Global bin number corresponding to binx,y,z.

2-D and 3-D histograms are represented with a one dimensional structure. This has the advantage that all existing functions, such as GetBinContent, GetBinError, GetBinFunction work for all dimensions.

In case of a TH1x, returns binx directly. see TH1::GetBinXYZ for the inverse transformation.

Convention for numbering bins

For all histogram types: nbins, xlow, xup

• bin = 0; underflow bin
• bin = 1; first bin with low-edge xlow INCLUDED
• bin = nbins; last bin with upper-edge xup EXCLUDED
• bin = nbins+1; overflow bin

In case of 2-D or 3-D histograms, a "global bin" number is defined. For example, assuming a 3-D histogram with binx,biny,binz, the function

Int_t bin = h->GetBin(binx,biny,binz);

returns a global/linearized bin number. This global bin is useful to access the bin information independently of the dimension.

Reimplemented in TH3, and TH2.

Definition at line 4893 of file TH1.cxx.

GetBinCenter()

Double_t TH1::GetBinCenter ( Int_t  bin ) const

virtual

Return bin center for 1D histogram.

Better to use h1.GetXaxis()->GetBinCenter(bin)

Definition at line 8981 of file TH1.cxx.

GetBinContent() [1/3]

Double_t TH1::GetBinContent ( Int_t  bin ) const

virtual

Return content of bin number bin.

Implemented in TH1C,S,F,D

Convention for numbering bins

For all histogram types: nbins, xlow, xup

• bin = 0; underflow bin
• bin = 1; first bin with low-edge xlow INCLUDED
• bin = nbins; last bin with upper-edge xup EXCLUDED
• bin = nbins+1; overflow bin

In case of 2-D or 3-D histograms, a "global bin" number is defined. For example, assuming a 3-D histogram with binx,biny,binz, the function

Int_t bin = h->GetBin(binx,biny,binz);

returns a global/linearized bin number. This global bin is useful to access the bin information independently of the dimension.

Reimplemented in TH1K, TH2, TH2Poly, TH3, TProfile, TProfile2D, TProfile2Poly, TProfile3D, and TProfile2Poly.

Definition at line 4993 of file TH1.cxx.

GetBinContent() [2/3]

virtual Double_t TH1::GetBinContent ( Int_t  bin, Int_t    ) const

inlinevirtual

Reimplemented in TH1K, TH3, TProfile, TH2, TProfile2D, TH2Poly, TProfile2Poly, and TProfile3D.

Definition at line 265 of file TH1.h.

GetBinContent() [3/3]

virtual Double_t TH1::GetBinContent ( Int_t  bin, Int_t  , Int_t    ) const

inlinevirtual

Reimplemented in TH1K, TProfile, TH3, TProfile3D, TH2, TProfile2D, TH2Poly, and TProfile2Poly.

Definition at line 266 of file TH1.h.

GetBinError() [1/3]

Double_t TH1::GetBinError ( Int_t  bin ) const

virtual

Return value of error associated to bin number bin.

if the sum of squares of weights has been defined (via Sumw2), this function returns the sqrt(sum of w2). otherwise it returns the sqrt(contents) for this bin.

Reimplemented in TH1K, TH2Poly, TProfile, TProfile2D, TProfile2Poly, TProfile3D, and TProfile2Poly.

Definition at line 8903 of file TH1.cxx.

GetBinError() [2/3]

virtual Double_t TH1::GetBinError ( Int_t  binx, Int_t  biny  ) const

inlinevirtual

Reimplemented in TH1K, TProfile, TProfile2D, TH2Poly, TProfile2Poly, and TProfile3D.

Definition at line 268 of file TH1.h.

GetBinError() [3/3]

virtual Double_t TH1::GetBinError ( Int_t  binx, Int_t  biny, Int_t  binz  ) const

inlinevirtual

Reimplemented in TH1K, TProfile, TProfile3D, TProfile2D, TH2Poly, and TProfile2Poly.

Definition at line 269 of file TH1.h.

GetBinErrorLow()

Double_t TH1::GetBinErrorLow ( Int_t  bin ) const

virtual

Return lower error associated to bin number bin.

The error will depend on the statistic option used will return the binContent - lower interval value

Reimplemented in TH2, and TH3.

Definition at line 8919 of file TH1.cxx.

GetBinErrorOption()

virtual EBinErrorOpt TH1::GetBinErrorOption ( ) const

inlinevirtual

Definition at line 272 of file TH1.h.

GetBinErrorSqUnchecked()

virtual Double_t TH1::GetBinErrorSqUnchecked ( Int_t  bin ) const

inlineprotectedvirtual

Reimplemented in TProfile, TProfile2D, and TProfile3D.

Definition at line 443 of file TH1.h.

GetBinErrorUp()

Double_t TH1::GetBinErrorUp ( Int_t  bin ) const

virtual

Return upper error associated to bin number bin.

The error will depend on the statistic option used will return the binContent - upper interval value

Reimplemented in TH2, and TH3.

Definition at line 8950 of file TH1.cxx.

GetBinLowEdge()

Double_t TH1::GetBinLowEdge ( Int_t  bin ) const

virtual

Return bin lower edge for 1D histogram.

Better to use h1.GetXaxis()->GetBinLowEdge(bin)

Definition at line 8992 of file TH1.cxx.

GetBinWidth()

Double_t TH1::GetBinWidth ( Int_t  bin ) const

virtual

Return bin width for 1D histogram.

Better to use h1.GetXaxis()->GetBinWidth(bin)

Definition at line 9003 of file TH1.cxx.

GetBinWithContent()

Double_t TH1::GetBinWithContent ( Double_t  c, Int_t &  binx, Int_t  firstx = 0, Int_t  lastx = 0, Double_t  maxdiff = 0  ) const

virtual

Compute first binx in the range [firstx,lastx] for which diff = abs(bin_content-c) <= maxdiff.

In case several bins in the specified range with diff=0 are found the first bin found is returned in binx. In case several bins in the specified range satisfy diff <=maxdiff the bin with the smallest difference is returned in binx. In all cases the function returns the smallest difference.

NOTE1: if firstx <= 0, firstx is set to bin 1 if (lastx < firstx then firstx is set to the number of bins ie if firstx=0 and lastx=0 (default) the search is on all bins.

NOTE2: if maxdiff=0 (default), the first bin with content=c is returned.

Definition at line 5018 of file TH1.cxx.

GetBinXYZ()

void TH1::GetBinXYZ ( Int_t  binglobal, Int_t &  binx, Int_t &  biny, Int_t &  binz  ) const

virtual

Return binx, biny, binz corresponding to the global bin number globalbin see TH1::GetBin function above.

Definition at line 4906 of file TH1.cxx.

GetBuffer()

const Double_t * TH1::GetBuffer ( ) const

inline

Definition at line 238 of file TH1.h.

GetBufferLength()

Int_t TH1::GetBufferLength ( ) const

inline

Definition at line 236 of file TH1.h.

GetBufferSize()

Int_t TH1::GetBufferSize ( ) const

inline

Definition at line 237 of file TH1.h.

GetCellContent()

virtual Double_t TH1::GetCellContent ( Int_t  binx, Int_t  biny  ) const

inlinevirtual

Definition at line 427 of file TH1.h.

GetCellError()

virtual Double_t TH1::GetCellError ( Int_t  binx, Int_t  biny  ) const

inlinevirtual

Definition at line 429 of file TH1.h.

GetCenter()

void TH1::GetCenter ( Double_t *  center ) const

virtual

Fill array with center of bins for 1D histogram Better to use h1.GetXaxis()->GetCenter(center)

Definition at line 9014 of file TH1.cxx.

GetContour()

Int_t TH1::GetContour ( Double_t *  levels = 0 )

virtual

Return contour values into array levels if pointer levels is non zero.

The function returns the number of contour levels. see GetContourLevel to return one contour only

Definition at line 8259 of file TH1.cxx.

GetContourLevel()

Double_t TH1::GetContourLevel ( Int_t  level ) const

virtual

Return value of contour number level.

Use GetContour to return the array of all contour levels

Definition at line 8278 of file TH1.cxx.

GetContourLevelPad()

Double_t TH1::GetContourLevelPad ( Int_t  level ) const

virtual

Return the value of contour number "level" in Pad coordinates.

ie: if the Pad is in log scale along Z it returns le log of the contour level value. See GetContour to return the array of all contour levels

Definition at line 8288 of file TH1.cxx.

GetCumulative()

TH1 * TH1::GetCumulative	(	Bool_t	forward = kTRUE,
		const char *	suffix = "_cumulative"
	)		const

Return a pointer to an histogram containing the cumulative content.

The cumulative can be computed both in the forward (default) or backward direction; the name of the new histogram is constructed from the name of this histogram with the suffix "suffix" appended provided by the user. If not provided a default suffix="_cumulative" is used.

The cumulative distribution is formed by filling each bin of the resulting histogram with the sum of that bin and all previous (forward == kTRUE) or following (forward = kFALSE) bins.

Note: while cumulative distributions make sense in one dimension, you may not be getting what you expect in more than 1D because the concept of a cumulative distribution is much trickier to define; make sure you understand the order of summation before you use this method with histograms of dimension >= 2.

Note 2: By default the cumulative is computed from bin 1 to Nbins If an axis range is set, values between the minimum and maximum of the range are set. Setting an axis range can also be used for including underflow and overflow in the cumulative (e.g. by setting h->GetXaxis()->SetRange(0, h->GetNbinsX()+1); )

Definition at line 2608 of file TH1.cxx.

GetDefaultBufferSize()

Int_t TH1::GetDefaultBufferSize ( )

static

Static function return the default buffer size for automatic histograms the parameter fgBufferSize may be changed via SetDefaultBufferSize.

Definition at line 4369 of file TH1.cxx.

GetDefaultSumw2()

Bool_t TH1::GetDefaultSumw2 ( )

static

Return kTRUE if TH1::Sumw2 must be called when creating new histograms.

see TH1::SetDefaultSumw2.

Definition at line 4378 of file TH1.cxx.

GetDimension()

virtual Int_t TH1::GetDimension ( ) const

inlinevirtual

Definition at line 282 of file TH1.h.

GetDirectory()

TDirectory * TH1::GetDirectory ( ) const

inline

Definition at line 278 of file TH1.h.

GetEffectiveEntries()

Double_t TH1::GetEffectiveEntries ( ) const

virtual

Number of effective entries of the histogram.

\[ neff = \frac{(\sum Weights )^2}{(\sum Weight^2 )} \]

In case of an unweighted histogram this number is equivalent to the number of entries of the histogram. For a weighted histogram, this number corresponds to the hypothetical number of unweighted entries a histogram would need to have the same statistical power as this weighted histogram. Note: The underflow/overflow are included if one has set the TH1::StatOverFlows flag and if the statistics has been computed at filling time. If a range is set in the histogram the number is computed from the given range.

Definition at line 4411 of file TH1.cxx.

GetEntries()

Double_t TH1::GetEntries ( ) const

virtual

Return the current number of entries.

Definition at line 4386 of file TH1.cxx.

GetFunction()

TF1 * TH1::GetFunction ( const char *  name ) const

virtual

Return pointer to function with name.

Functions such as TH1::Fit store the fitted function in the list of functions of this histogram.

Definition at line 8891 of file TH1.cxx.

GetIntegral()

Double_t * TH1::GetIntegral ( )

virtual

Return a pointer to the array of bins integral.

if the pointer fIntegral is null, TH1::ComputeIntegral is called The array dimension is the number of bins in the histograms including underflow and overflow (fNCells) the last value integral[fNCells] is set to the number of entries of the histogram

Definition at line 2578 of file TH1.cxx.

GetKurtosis()

Double_t TH1::GetKurtosis ( Int_t  axis = 1 ) const

virtual

• For axis =1, 2 or 3 returns kurtosis of the histogram along x, y or z axis. Kurtosis(gaussian(0, 1)) = 0.
• For axis =11, 12 or 13 returns the approximate standard error of kurtosis of the histogram along x, y or z axis

Note, that since third and fourth moment are not calculated at the fill time, kurtosis and its standard error are computed bin by bin

IMPORTANT NOTE: The returned value depends on how the histogram statistics are calculated. See TH1::GetMean and TH1::GetStdDev.

Definition at line 7637 of file TH1.cxx.

GetLabelColor()

Color_t TH1::GetLabelColor ( Option_t *  axis = "X" ) const

virtual

Return the "axis" label color.

Definition at line 53 of file Haxis.cxx.

GetLabelFont()

Style_t TH1::GetLabelFont ( Option_t *  axis = "X" ) const

virtual

Return the "axis" label font.

Definition at line 66 of file Haxis.cxx.

GetLabelOffset()

Float_t TH1::GetLabelOffset ( Option_t *  axis = "X" ) const

virtual

Return the "axis" label offset.

Definition at line 79 of file Haxis.cxx.

GetLabelSize()

Float_t TH1::GetLabelSize ( Option_t *  axis = "X" ) const

virtual

Return the "axis" label size.

Definition at line 92 of file Haxis.cxx.

GetListOfFunctions()

TList * TH1::GetListOfFunctions ( ) const

inline

Definition at line 243 of file TH1.h.

GetLowEdge()

void TH1::GetLowEdge ( Double_t *  edge ) const

virtual

Fill array with low edge of bins for 1D histogram Better to use h1.GetXaxis()->GetLowEdge(edge)

Definition at line 9027 of file TH1.cxx.

GetMaximum()

Double_t TH1::GetMaximum ( Double_t  maxval = FLT_MAX ) const

virtual

Return maximum value smaller than maxval of bins in the range, unless the value has been overridden by TH1::SetMaximum, in which case it returns that value.

(This happens, for example, when the histogram is drawn and the y or z axis limits are changed

To get the maximum value of bins in the histogram regardless of whether the value has been overridden, use

h->GetBinContent(h->GetMaximumBin())

Reimplemented in TH2Poly.

Definition at line 8390 of file TH1.cxx.

GetMaximumBin() [1/2]

Int_t TH1::GetMaximumBin ( ) const

virtual

Return location of bin with maximum value in the range.

Definition at line 8420 of file TH1.cxx.

GetMaximumBin() [2/2]

Int_t TH1::GetMaximumBin ( Int_t &  locmax, Int_t &  locmay, Int_t &  locmaz  ) const

virtual

Return location of bin with maximum value in the range.

Definition at line 8429 of file TH1.cxx.

GetMaximumStored()

virtual Double_t TH1::GetMaximumStored ( ) const

inlinevirtual

Definition at line 288 of file TH1.h.

GetMean()

Double_t TH1::GetMean ( Int_t  axis = 1 ) const

virtual

For axis = 1,2 or 3 returns the mean value of the histogram along X,Y or Z axis.

For axis = 11, 12, 13 returns the standard error of the mean value of the histogram along X, Y or Z axis

Note that the mean value/StdDev is computed using the bins in the currently defined range (see TAxis::SetRange). By default the range includes all bins from 1 to nbins included, excluding underflows and overflows. To force the underflows and overflows in the computation, one must call the static function TH1::StatOverflows(kTRUE) before filling the histogram.

IMPORTANT NOTE: The returned value depends on how the histogram statistics are calculated. By default, if no range has been set, the returned mean is the (unbinned) one calculated at fill time. If a range has been set, however, the mean is calculated using the bins in range, as described above; THIS IS TRUE EVEN IF THE RANGE INCLUDES ALL BINS–use TAxis::SetRange(0, 0) to unset the range. To ensure that the returned mean (and all other statistics) is always that of the binned data stored in the histogram, call TH1::ResetStats. See TH1::GetStats.

Return mean value of this histogram along the X axis.

Note that the mean value/StdDev is computed using the bins in the currently defined range (see TAxis::SetRange). By default the range includes all bins from 1 to nbins included, excluding underflows and overflows. To force the underflows and overflows in the computation, one must call the static function TH1::StatOverflows(kTRUE) before filling the histogram.

Definition at line 7428 of file TH1.cxx.

GetMeanError()

Double_t TH1::GetMeanError ( Int_t  axis = 1 ) const

virtual

Return standard error of mean of this histogram along the X axis.

Note that the mean value/StdDev is computed using the bins in the currently defined range (see TAxis::SetRange). By default the range includes all bins from 1 to nbins included, excluding underflows and overflows. To force the underflows and overflows in the computation, one must call the static function TH1::StatOverflows(kTRUE) before filling the histogram.

Also note, that although the definition of standard error doesn't include the assumption of normality, many uses of this feature implicitly assume it.

IMPORTANT NOTE: The returned value depends on how the histogram statistics are calculated. By default, if no range has been set, the returned value is the (unbinned) one calculated at fill time. If a range has been set, however, the value is calculated using the bins in range, as described above; THIS IS TRUE EVEN IF THE RANGE INCLUDES ALL BINS–use TAxis::SetRange(0, 0) to unset the range. To ensure that the returned value (and all other statistics) is always that of the binned data stored in the histogram, call TH1::ResetStats. See TH1::GetStats.

Definition at line 7468 of file TH1.cxx.

GetMinimum()

Double_t TH1::GetMinimum ( Double_t  minval = -FLT_MAX ) const

virtual

Return minimum value larger than minval of bins in the range, unless the value has been overridden by TH1::SetMinimum, in which case it returns that value.

(This happens, for example, when the histogram is drawn and the y or z axis limits are changed

To get the minimum value of bins in the histogram regardless of whether the value has been overridden, use

h->GetBinContent(h->GetMinimumBin())

Reimplemented in TH2Poly.

Definition at line 8475 of file TH1.cxx.

GetMinimumAndMaximum()

void TH1::GetMinimumAndMaximum ( Double_t &  min, Double_t &  max  ) const

virtual

Retrieve the minimum and maximum values in the histogram.

This will not return a cached value and will always search the histogram for the min and max values. The user can condition whether or not to call this with the GetMinimumStored() and GetMaximumStored() methods. If the cache is empty, then the value will be -1111. Users can then use the SetMinimum() or SetMaximum() methods to cache the results. For example, the following recipe will make efficient use of this method and the cached minimum and maximum values.

Double_t currentMin = pHist->GetMinimumStored();
Double_t currentMax = pHist->GetMaximumStored();
if ((currentMin == -1111) || (currentMax == -1111)) {
   pHist->GetMinimumAndMaximum(currentMin, currentMax);
   pHist->SetMinimum(currentMin);
   pHist->SetMaximum(currentMax);
}

Parameters

min	reference to variable that will hold found minimum value
max	reference to variable that will hold found maximum value

Definition at line 8571 of file TH1.cxx.

GetMinimumBin() [1/2]

Int_t TH1::GetMinimumBin ( ) const

virtual

Return location of bin with minimum value in the range.

Definition at line 8505 of file TH1.cxx.

GetMinimumBin() [2/2]

Int_t TH1::GetMinimumBin ( Int_t &  locmix, Int_t &  locmiy, Int_t &  locmiz  ) const

virtual

Return location of bin with minimum value in the range.

Definition at line 8514 of file TH1.cxx.

GetMinimumStored()

virtual Double_t TH1::GetMinimumStored ( ) const

inlinevirtual

Definition at line 292 of file TH1.h.

GetNbinsX()

virtual Int_t TH1::GetNbinsX ( ) const

inlinevirtual

Definition at line 296 of file TH1.h.

GetNbinsY()

virtual Int_t TH1::GetNbinsY ( ) const

inlinevirtual

Definition at line 297 of file TH1.h.

GetNbinsZ()

virtual Int_t TH1::GetNbinsZ ( ) const

inlinevirtual

Definition at line 298 of file TH1.h.

GetNcells()

virtual Int_t TH1::GetNcells ( ) const

inlinevirtual

Definition at line 299 of file TH1.h.

GetNdivisions()

Int_t TH1::GetNdivisions ( Option_t *  axis = "X" ) const

virtual

Return the number of divisions for "axis".

Definition at line 27 of file Haxis.cxx.

GetNormFactor()

virtual Double_t TH1::GetNormFactor ( ) const

inlinevirtual

Definition at line 300 of file TH1.h.

GetObjectInfo()

char * TH1::GetObjectInfo ( Int_t  px, Int_t  py  ) const

virtual

Redefines TObject::GetObjectInfo.

Displays the histogram info (bin number, contents, integral up to bin corresponding to cursor position px,py

Reimplemented from TObject.

Reimplemented in TGLTH3Composition.

Definition at line 4443 of file TH1.cxx.

GetOption()

Option_t * TH1::GetOption ( ) const

inlinevirtual

Reimplemented from TObject.

Definition at line 302 of file TH1.h.

GetPainter()

TVirtualHistPainter * TH1::GetPainter

(

Option_t *

option = ""

)

Return pointer to painter.

If painter does not exist, it is created

Definition at line 4452 of file TH1.cxx.

GetQuantiles()

Int_t TH1::GetQuantiles ( Int_t  nprobSum, Double_t *  q, const Double_t *  probSum = 0  )

virtual

Compute Quantiles for this histogram Quantile x_q of a probability distribution Function F is defined as.

F(x_q) = q with 0 <= q <= 1.

For instance the median x_0.5 of a distribution is defined as that value of the random variable for which the distribution function equals 0.5:

F(x_0.5) = Probability(x < x_0.5) = 0.5

code from Eddy Offermann, Renaissance

Parameters

[in]	nprobSum	maximum size of array q and size of array probSum (if given)
[in]	probSum	array of positions where quantiles will be computed. if probSum is null, probSum will be computed internally and will have a size = number of bins + 1 in h. it will correspond to the quantiles calculated at the lowest edge of the histogram (quantile=0) and all the upper edges of the bins. if probSum is not null, it is assumed to contain at least nprobSum values.
[out]	q	array q filled with nq quantiles

Returns

value nq (<=nprobSum) with the number of quantiles computed

Note that the Integral of the histogram is automatically recomputed if the number of entries is different of the number of entries when the integral was computed last time. In case you do not use the Fill functions to fill your histogram, but SetBinContent, you must call TH1::ComputeIntegral before calling this function.

Getting quantiles q from two histograms and storing results in a TGraph, a so-called QQ-plot

TGraph *gr = new TGraph(nprob);
h1->GetQuantiles(nprob,gr->GetX());
h2->GetQuantiles(nprob,gr->GetY());
gr->Draw("alp");

Example:

void quantiles() {
   // demo for quantiles
   const Int_t nq = 20;
   TH1F *h = new TH1F("h","demo quantiles",100,-3,3);
   h->FillRandom("gaus",5000);
 
   Double_t xq[nq];  // position where to compute the quantiles in [0,1]
   Double_t yq[nq];  // array to contain the quantiles
   for (Int_t i=0;i<nq;i++) xq[i] = Float_t(i+1)/nq;
   h->GetQuantiles(nq,yq,xq);
 
   //show the original histogram in the top pad
   TCanvas *c1 = new TCanvas("c1","demo quantiles",10,10,700,900);
   c1->Divide(1,2);
   c1->cd(1);
   h->Draw();
 
   // show the quantiles in the bottom pad
   c1->cd(2);
   gPad->SetGrid();
   TGraph *gr = new TGraph(nq,xq,yq);
   gr->SetMarkerStyle(21);
   gr->Draw("alp");
}

Definition at line 4543 of file TH1.cxx.

GetRandom()

Double_t TH1::GetRandom ( TRandom *  rng = nullptr ) const

virtual

Return a random number distributed according the histogram bin contents.

This function checks if the bins integral exists. If not, the integral is evaluated, normalized to one.

Parameters

rng	(optional) Random number generator pointer used (default is gRandom)

The integral is automatically recomputed if the number of entries is not the same then when the integral was computed. NB Only valid for 1-d histograms. Use GetRandom2 or 3 otherwise. If the histogram has a bin with negative content a NaN is returned

Definition at line 4942 of file TH1.cxx.

GetRMS()

Double_t TH1::GetRMS ( Int_t  axis = 1 ) const

inline

Definition at line 315 of file TH1.h.

GetRMSError()

Double_t TH1::GetRMSError ( Int_t  axis = 1 ) const

inline

Definition at line 316 of file TH1.h.

GetSkewness()

Double_t TH1::GetSkewness ( Int_t  axis = 1 ) const

virtual

• For axis = 1, 2 or 3 returns skewness of the histogram along x, y or z axis.
• For axis = 11, 12 or 13 returns the approximate standard error of skewness of the histogram along x, y or z axis

Note, that since third and fourth moment are not calculated at the fill time, skewness and its standard error are computed bin by bin

IMPORTANT NOTE: The returned value depends on how the histogram statistics are calculated. See TH1::GetMean and TH1::GetStdDev.

Definition at line 7564 of file TH1.cxx.

GetStatOverflows()

EStatOverflows TH1::GetStatOverflows ( ) const

inline

Definition at line 319 of file TH1.h.

GetStatOverflowsBehaviour()

Bool_t TH1::GetStatOverflowsBehaviour ( ) const

inlineprotected

Definition at line 152 of file TH1.h.

GetStats()

void TH1::GetStats ( Double_t *  stats ) const

virtual

fill the array stats from the contents of this histogram The array stats must be correctly dimensioned in the calling program.

stats[0] = sumw
stats[1] = sumw2
stats[2] = sumwx
stats[3] = sumwx2

If no axis-subrange is specified (via TAxis::SetRange), the array stats is simply a copy of the statistics quantities computed at filling time. If a sub-range is specified, the function recomputes these quantities from the bin contents in the current axis range.

IMPORTANT NOTE: This means that the returned statistics are context-dependent. If TAxis::kAxisRange, the returned statistics are dependent on the binning; otherwise, they are a copy of the histogram statistics computed at fill time, which are unbinned by default (calling TH1::ResetStats forces them to use binned statistics). You can reset TAxis::kAxisRange using TAxis::SetRange(0, 0).

Note that the mean value/StdDev is computed using the bins in the currently defined range (see TAxis::SetRange). By default the range includes all bins from 1 to nbins included, excluding underflows and overflows. To force the underflows and overflows in the computation, one must call the static function TH1::StatOverflows(kTRUE) before filling the histogram.

Reimplemented in TH2, TH2Poly, TH3, TProfile, TProfile2D, TProfile3D, and TProfile2Poly.

Definition at line 7726 of file TH1.cxx.

GetStdDev()

Double_t TH1::GetStdDev ( Int_t  axis = 1 ) const

virtual

Returns the Standard Deviation (Sigma).

The Sigma estimate is computed as

\[ \sqrt{\frac{1}{N}(\sum(x_i-x_{mean})^2)} \]

For axis = 1,2 or 3 returns the Sigma value of the histogram along X, Y or Z axis For axis = 11, 12 or 13 returns the error of StdDev estimation along X, Y or Z axis for Normal distribution

Note that the mean value/sigma is computed using the bins in the currently defined range (see TAxis::SetRange). By default the range includes all bins from 1 to nbins included, excluding underflows and overflows. To force the underflows and overflows in the computation, one must call the static function TH1::StatOverflows(kTRUE) before filling the histogram.

IMPORTANT NOTE: The returned value depends on how the histogram statistics are calculated. By default, if no range has been set, the returned standard deviation is the (unbinned) one calculated at fill time. If a range has been set, however, the standard deviation is calculated using the bins in range, as described above; THIS IS TRUE EVEN IF THE RANGE INCLUDES ALL BINS–use TAxis::SetRange(0, 0) to unset the range. To ensure that the returned standard deviation (and all other statistics) is always that of the binned data stored in the histogram, call TH1::ResetStats. See TH1::GetStats.

Definition at line 7500 of file TH1.cxx.

GetStdDevError()

Double_t TH1::GetStdDevError ( Int_t  axis = 1 ) const

virtual

Return error of standard deviation estimation for Normal distribution.

Note that the mean value/StdDev is computed using the bins in the currently defined range (see TAxis::SetRange). By default the range includes all bins from 1 to nbins included, excluding underflows and overflows. To force the underflows and overflows in the computation, one must call the static function TH1::StatOverflows(kTRUE) before filling the histogram.

Value returned is standard deviation of sample standard deviation. Note that it is an approximated value which is valid only in the case that the original data distribution is Normal. The correct one would require the 4-th momentum value, which cannot be accurately estimated from an histogram since the x-information for all entries is not kept.

IMPORTANT NOTE: The returned value depends on how the histogram statistics are calculated. By default, if no range has been set, the returned value is the (unbinned) one calculated at fill time. If a range has been set, however, the value is calculated using the bins in range, as described above; THIS IS TRUE EVEN IF THE RANGE INCLUDES ALL BINS–use TAxis::SetRange(0, 0) to unset the range. To ensure that the returned value (and all other statistics) is always that of the binned data stored in the histogram, call TH1::ResetStats. See TH1::GetStats.

Definition at line 7548 of file TH1.cxx.

GetSumOfWeights()

Double_t TH1::GetSumOfWeights ( ) const

virtual

Return the sum of weights excluding under/overflows.

Definition at line 7810 of file TH1.cxx.

GetSumw2() [1/2]

virtual TArrayD * TH1::GetSumw2 ( )

inlinevirtual

Definition at line 312 of file TH1.h.

GetSumw2() [2/2]

virtual const TArrayD * TH1::GetSumw2 ( ) const

inlinevirtual

Definition at line 313 of file TH1.h.

GetSumw2N()

virtual Int_t TH1::GetSumw2N ( ) const

inlinevirtual

Definition at line 314 of file TH1.h.

GetTickLength()

Float_t TH1::GetTickLength ( Option_t *  axis = "X" ) const

virtual

Return the "axis" tick length.

Definition at line 105 of file Haxis.cxx.

GetTitleFont()

Style_t TH1::GetTitleFont ( Option_t *  axis = "X" ) const

virtual

Return the "axis" title font.

Definition at line 118 of file Haxis.cxx.

GetTitleOffset()

Float_t TH1::GetTitleOffset ( Option_t *  axis = "X" ) const

virtual

Return the "axis" title offset.

Definition at line 131 of file Haxis.cxx.

GetTitleSize()

Float_t TH1::GetTitleSize ( Option_t *  axis = "X" ) const

virtual

Return the "axis" title size.

Definition at line 144 of file Haxis.cxx.

GetXaxis() [1/2]

TAxis * TH1::GetXaxis ( )

inline

Get the behaviour adopted by the object about the statoverflows. See EStatOverflows for more information.

Definition at line 320 of file TH1.h.

GetXaxis() [2/2]

const TAxis * TH1::GetXaxis ( ) const

inline

Definition at line 323 of file TH1.h.

GetYaxis() [1/2]

TAxis * TH1::GetYaxis ( )

inline

Definition at line 321 of file TH1.h.

GetYaxis() [2/2]

const TAxis * TH1::GetYaxis ( ) const

inline

Definition at line 324 of file TH1.h.

GetZaxis() [1/2]

TAxis * TH1::GetZaxis ( )

inline

Definition at line 322 of file TH1.h.

GetZaxis() [2/2]

const TAxis * TH1::GetZaxis ( ) const

inline

Definition at line 325 of file TH1.h.

Integral() [1/2]

Double_t TH1::Integral ( Int_t  binx1, Int_t  binx2, Option_t *  option = ""  ) const

virtual

Return integral of bin contents in range [binx1,binx2].

By default the integral is computed as the sum of bin contents in the range. if option "width" is specified, the integral is the sum of the bin contents multiplied by the bin width in x.

Reimplemented in TH2, and TH3.

Definition at line 7846 of file TH1.cxx.

Integral() [2/2]

Double_t TH1::Integral ( Option_t *  option = "" ) const

virtual

Return integral of bin contents.

Only bins in the bins range are considered.

By default the integral is computed as the sum of bin contents in the range. if option "width" is specified, the integral is the sum of the bin contents multiplied by the bin width in x.

Reimplemented in TH2, TH2, TH2Poly, TH3, and TH3.

Definition at line 7834 of file TH1.cxx.

IntegralAndError()

Double_t TH1::IntegralAndError ( Int_t  binx1, Int_t  binx2, Double_t &  error, Option_t *  option = ""  ) const

virtual

Return integral of bin contents in range [binx1,binx2] and its error.

By default the integral is computed as the sum of bin contents in the range. if option "width" is specified, the integral is the sum of the bin contents multiplied by the bin width in x. the error is computed using error propagation from the bin errors assuming that all the bins are uncorrelated

Reimplemented in TH2, and TH3.

Definition at line 7861 of file TH1.cxx.

Interpolate() [1/3]

Double_t TH1::Interpolate ( Double_t  x ) const

virtual

Given a point x, approximates the value via linear interpolation based on the two nearest bin centers.

Andy Mastbaum 10/21/08

Reimplemented in TH2, TH2Poly, and TH3.

Definition at line 5047 of file TH1.cxx.

Interpolate() [2/3]

Double_t TH1::Interpolate ( Double_t  x, Double_t  y  ) const

virtual

2d Interpolation. Not yet implemented.

Reimplemented in TH2, TH2Poly, and TH3.

Definition at line 5077 of file TH1.cxx.

Interpolate() [3/3]

Double_t TH1::Interpolate ( Double_t  x, Double_t  y, Double_t  z  ) const

virtual

3d Interpolation. Not yet implemented.

Reimplemented in TH2, TH2Poly, and TH3.

Definition at line 5086 of file TH1.cxx.

IsBinOverflow()

Bool_t TH1::IsBinOverflow	(	Int_t	bin,
		Int_t	axis = 0
	)		const

Return true if the bin is overflow.

Definition at line 5114 of file TH1.cxx.

IsBinUnderflow()

Bool_t TH1::IsBinUnderflow	(	Int_t	bin,
		Int_t	iaxis = 0
	)		const

Return true if the bin is underflow.

If iaxis = 0 make OR with all axes otherwise check only for the given axis

Definition at line 5146 of file TH1.cxx.

IsEmpty()

Bool_t TH1::IsEmpty ( ) const

protected

Check if an histogram is empty (this a protected method used mainly by TH1Merger )

Definition at line 5096 of file TH1.cxx.

IsHighlight()

virtual Bool_t TH1::IsHighlight ( ) const

inlinevirtual

Definition at line 334 of file TH1.h.

KolmogorovTest()

Double_t TH1::KolmogorovTest ( const TH1 *  h2, Option_t *  option = ""  ) const

virtual

Statistical test of compatibility in shape between this histogram and h2, using Kolmogorov test.

Note that the KolmogorovTest (KS) test should in theory be used only for unbinned data and not for binned data as in the case of the histogram (see NOTE 3 below). So, before using this method blindly, read the NOTE 3.

Default: Ignore under- and overflow bins in comparison

Parameters

[in]	h2	histogram
[in]	option	is a character string to specify options "U" include Underflows in test (also for 2-dim) "O" include Overflows (also valid for 2-dim) "N" include comparison of normalizations "D" Put out a line of "Debug" printout "M" Return the Maximum Kolmogorov distance instead of prob "X" Run the pseudo experiments post-processor with the following procedure: make pseudoexperiments based on random values from the parent distribution, compare the KS distance of the pseudoexperiment to the parent distribution, and count all the KS values above the value obtained from the original data to Monte Carlo distribution. The number of pseudo-experiments nEXPT is currently fixed at 1000. The function returns the probability. (thanks to Ben Kilminster to submit this procedure). Note that this option "X" is much slower.

The returned function value is the probability of test (much less than one means NOT compatible)

Code adapted by Rene Brun from original HBOOK routine HDIFF

NOTE1 A good description of the Kolmogorov test can be seen at: http://www.itl.nist.gov/div898/handbook/eda/section3/eda35g.htm

NOTE2 see also alternative function TH1::Chi2Test The Kolmogorov test is assumed to give better results than Chi2Test in case of histograms with low statistics.

NOTE3 (Jan Conrad, Fred James) "The returned value PROB is calculated such that it will be uniformly distributed between zero and one for compatible histograms, provided the data are not binned (or the number of bins is very large compared with the number of events). Users who have access to unbinned data and wish exact confidence levels should therefore not put their data into histograms, but should call directly TMath::KolmogorovTest. On the other hand, since TH1 is a convenient way of collecting data and saving space, this function has been provided. However, the values of PROB for binned data will be shifted slightly higher than expected, depending on the effects of the binning. For example, when comparing two uniform distributions of 500 events in 100 bins, the values of PROB, instead of being exactly uniformly distributed between zero and one, have a mean value of about 0.56. We can apply a useful rule: As long as the bin width is small compared with any significant physical effect (for example the experimental resolution) then the binning cannot have an important effect. Therefore, we believe that for all practical purposes, the probability value PROB is calculated correctly provided the user is aware that: 1. The value of PROB should not be expected to have exactly the correct distribution for binned data. 2. The user is responsible for seeing to it that the bin widths are small compared with any physical phenomena of interest. 3. The effect of binning (if any) is always to make the value of PROB slightly too big. That is, setting an acceptance criterion of (PROB>0.05 will assure that at most 5% of truly compatible histograms are rejected, and usually somewhat less."

Note also that for GoF test of unbinned data ROOT provides also the class ROOT::Math::GoFTest. The class has also method for doing one sample tests (i.e. comparing the data with a given distribution).

Reimplemented in TH2, and TH3.

Definition at line 8068 of file TH1.cxx.

LabelsDeflate()

void TH1::LabelsDeflate ( Option_t *  ax = "X" )

virtual

Reduce the number of bins for the axis passed in the option to the number of bins having a label.

The method will remove only the extra bins existing after the last "labeled" bin. Note that if there are "un-labeled" bins present between "labeled" bins they will not be removed

Reimplemented in TProfile, TProfile2D, and TProfile3D.

Definition at line 5177 of file TH1.cxx.

LabelsInflate()

void TH1::LabelsInflate ( Option_t *  ax = "X" )

virtual

Double the number of bins for axis.

Refill histogram This function is called by TAxis::FindBin(const char *label)

Reimplemented in TProfile, TProfile2D, and TProfile3D.

Definition at line 5247 of file TH1.cxx.

LabelsOption()

void TH1::LabelsOption ( Option_t *  option = "h", Option_t *  ax = "X"  )

virtual

Sort bins with labels or set option(s) to draw axis with labels.

Parameters

[in]

option

"a" sort by alphabetic order ">" sort by decreasing values "<" sort by increasing values "h" draw labels horizontal "v" draw labels vertical "u" draw labels up (end of label right adjusted) "d" draw labels down (start of label left adjusted)

In case not all bins have labels sorting will work only in the case the first n consecutive bins have all labels and sorting will be performed on those label bins.

Parameters

[in]

ax

axis

Reimplemented in TProfile, TProfile2D, and TProfile3D.

Definition at line 5313 of file TH1.cxx.

Merge() [1/2]

virtual Long64_t TH1::Merge ( TCollection *  list )

inlinevirtual

Reimplemented in TH2Poly, TProfile2Poly, TProfile, TProfile2D, and TProfile3D.

Definition at line 341 of file TH1.h.

Merge() [2/2]

Long64_t TH1::Merge	(	TCollection *	li,
		Option_t *	opt
	)

Add all histograms in the collection to this histogram.

This function computes the min/max for the x axis, compute a new number of bins, if necessary, add bin contents, errors and statistics. If all histograms have bin labels, bins with identical labels will be merged, no matter what their order is. If overflows are present and limits are different the function will fail. The function returns the total number of entries in the result histogram if the merge is successful, -1 otherwise.

Possible option: -NOL : the merger will ignore the labels and merge the histograms bin by bin using bin center values to match bins -NOCHECK: the histogram will not perform a check for duplicate labels in case of axes with labels. The check (enabled by default) slows down the merging

IMPORTANT remark. The axis x may have different number of bins and different limits, BUT the largest bin width must be a multiple of the smallest bin width and the upper limit must also be a multiple of the bin width. Example:

void atest() {
  TH1F *h1 = new TH1F("h1","h1",110,-110,0);
  TH1F *h2 = new TH1F("h2","h2",220,0,110);
  TH1F *h3 = new TH1F("h3","h3",330,-55,55);
  TRandom r;
  for (Int_t i=0;i<10000;i++) {
     h1->Fill(r.Gaus(-55,10));
     h2->Fill(r.Gaus(55,10));
     h3->Fill(r.Gaus(0,10));
  }
 
  TList *list = new TList;
  list->Add(h1);
  list->Add(h2);
  list->Add(h3);
  TH1F *h = (TH1F*)h1->Clone("h");
  h->Reset();
  h->Merge(list);
  h->Draw();
}

Definition at line 5953 of file TH1.cxx.

Multiply() [1/3]

Bool_t TH1::Multiply ( const TH1 *  h1 )

virtual

Multiply this histogram by h1.

this = this*h1

If errors of this are available (TH1::Sumw2), errors are recalculated. Note that if h1 has Sumw2 set, Sumw2 is automatically called for this if not already set.

IMPORTANT NOTE: If you intend to use the errors of this histogram later you should call Sumw2 before making this operation. This is particularly important if you fit the histogram after TH1::Multiply

The function return kFALSE if the Multiply operation failed

Reimplemented in TProfile, TProfile2D, and TProfile3D.

Definition at line 6042 of file TH1.cxx.

Multiply() [2/3]

Bool_t TH1::Multiply ( const TH1 *  h1, const TH1 *  h2, Double_t  c1 = 1, Double_t  c2 = 1, Option_t *  option = ""  )

virtual

Replace contents of this histogram by multiplication of h1 by h2.

this = (c1*h1)*(c2*h2)

If errors of this are available (TH1::Sumw2), errors are recalculated. Note that if h1 or h2 have Sumw2 set, Sumw2 is automatically called for this if not already set.

IMPORTANT NOTE: If you intend to use the errors of this histogram later you should call Sumw2 before making this operation. This is particularly important if you fit the histogram after TH1::Multiply

The function return kFALSE if the Multiply operation failed

Reimplemented in TProfile, TProfile2D, and TProfile3D.

Definition at line 6100 of file TH1.cxx.

Multiply() [3/3]

Bool_t TH1::Multiply ( TF1 *  f1, Double_t  c1 = 1  )

virtual

Performs the operation:

this = this*c1*f1

If errors are defined (see TH1::Sumw2), errors are also recalculated.

Only bins inside the function range are recomputed. IMPORTANT NOTE: If you intend to use the errors of this histogram later you should call Sumw2 before making this operation. This is particularly important if you fit the histogram after TH1::Multiply

The function return kFALSE if the Multiply operation failed

Reimplemented in TH2Poly, TProfile, TProfile2D, and TProfile3D.

Definition at line 5980 of file TH1.cxx.

operator=()

TH1 & TH1::operator= ( const TH1 &  )

private

Paint()

void TH1::Paint ( Option_t *  option = "" )

virtual

Control routine to paint any kind of histograms.

This function is automatically called by TCanvas::Update. (see TH1::Draw for the list of options)

Reimplemented from TObject.

Reimplemented in TGLTH3Composition.

Definition at line 6155 of file TH1.cxx.

Print()

void TH1::Print ( Option_t *  option = "" ) const

virtual

Print some global quantities for this histogram.

Parameters

[in]

option

"base" is given, number of bins and ranges are also printed "range" is given, bin contents and errors are also printed for all bins in the current range (default 1-->nbins) "all" is given, bin contents and errors are also printed for all bins including under and overflows.

Reimplemented from TNamed.

Definition at line 6975 of file TH1.cxx.

PutStats()

void TH1::PutStats ( Double_t *  stats )

virtual

Replace current statistics with the values in array stats.

Reimplemented in TH2, TH3, TProfile, TProfile2D, and TProfile3D.

Definition at line 7777 of file TH1.cxx.

Rebin()

TH1 * TH1::Rebin ( Int_t  ngroup = 2, const char *  newname = "", const Double_t *  xbins = 0  )

virtual

Rebin this histogram.

case 1 xbins=0

If newname is blank (default), the current histogram is modified and a pointer to it is returned.

If newname is not blank, the current histogram is not modified, and a new histogram is returned which is a Clone of the current histogram with its name set to newname.

The parameter ngroup indicates how many bins of this have to be merged into one bin of the result.

If the original histogram has errors stored (via Sumw2), the resulting histograms has new errors correctly calculated.

examples: if h1 is an existing TH1F histogram with 100 bins

h1->Rebin();  //merges two bins in one in h1: previous contents of h1 are lost
h1->Rebin(5); //merges five bins in one in h1
TH1F *hnew = dynamic_cast<TH1F*>(h1->Rebin(5,"hnew")); // creates a new histogram hnew
                                                       // merging 5 bins of h1 in one bin

NOTE: If ngroup is not an exact divider of the number of bins, the top limit of the rebinned histogram is reduced to the upper edge of the last bin that can make a complete group. The remaining bins are added to the overflow bin. Statistics will be recomputed from the new bin contents.

case 2 xbins!=0

A new histogram is created (you should specify newname). The parameter ngroup is the number of variable size bins in the created histogram. The array xbins must contain ngroup+1 elements that represent the low-edges of the bins. If the original histogram has errors stored (via Sumw2), the resulting histograms has new errors correctly calculated.

NOTE: The bin edges specified in xbins should correspond to bin edges in the original histogram. If a bin edge in the new histogram is in the middle of a bin in the original histogram, all entries in the split bin in the original histogram will be transfered to the lower of the two possible bins in the new histogram. This is probably not what you want. A warning message is emitted in this case

examples: if h1 is an existing TH1F histogram with 100 bins

Double_t xbins[25] = {...} array of low-edges (xbins[25] is the upper edge of last bin
h1->Rebin(24,"hnew",xbins);  //creates a new variable bin size histogram hnew

Reimplemented in TH2, and TProfile.

Definition at line 6222 of file TH1.cxx.

RebinAxis()

virtual void TH1::RebinAxis ( Double_t  x, TAxis *  axis  )

inlinevirtual

Definition at line 431 of file TH1.h.

RebinX()

virtual TH1 * TH1::RebinX ( Int_t  ngroup = 2, const char *  newname = ""  )

inlinevirtual

Reimplemented in TH2, TH3, and TProfile2D.

Definition at line 350 of file TH1.h.

Rebuild()

void TH1::Rebuild ( Option_t *  option = "" )

virtual

Using the current bin info, recompute the arrays for contents and errors.

Definition at line 7053 of file TH1.cxx.

RecomputeAxisLimits()

Bool_t TH1::RecomputeAxisLimits ( TAxis &  destAxis, const TAxis &  anAxis  )

staticprotected

Finds new limits for the axis for the Merge function.

returns false if the limits are incompatible

Definition at line 5839 of file TH1.cxx.

RecursiveRemove()

void TH1::RecursiveRemove ( TObject *  obj )

virtual

Recursively remove object from the list of functions.

Reimplemented from TObject.

Definition at line 6536 of file TH1.cxx.

Reset()

void TH1::Reset ( Option_t *  option = "" )

virtual

Reset this histogram: contents, errors, etc.

Parameters

[in]

option

if "ICE" is specified, resets only Integral, Contents and Errors. if "ICES" is specified, resets only Integral, Contents, Errors and Statistics This option is used if "M" is specified, resets also Minimum and Maximum

Reimplemented in TH2Poly, TH1C, TH1S, TH1I, TH1F, TH1D, TH1K, TH2, TH2C, TH2S, TH2I, TH2F, TH2D, TH3, TH3C, TH3S, TH3I, TH3F, TH3D, TProfile, TProfile2D, TProfile3D, and TProfile2Poly.

Definition at line 7069 of file TH1.cxx.

ResetStats()

void TH1::ResetStats ( )

virtual

Reset the statistics including the number of entries and replace with values calculated from bin content.

The number of entries is set to the total bin content or (in case of weighted histogram) to number of effective entries

Note that, by default, before calling this function, statistics are those computed at fill time, which are unbinned. See TH1::GetStats.

Definition at line 7795 of file TH1.cxx.

RetrieveBinContent()

Double_t TH1::RetrieveBinContent ( Int_t  bin ) const

protectedvirtual

Raw retrieval of bin content on internal data structure see convention for numbering bins in TH1::GetBin.

Reimplemented in TH1C, TH1S, TH1I, TH1F, TH1D, TH2C, TH2S, TH2I, TH2F, TH2D, TH2Poly, TH3C, TH3S, TH3I, TH3F, TH3D, TProfile, TProfile2D, and TProfile3D.

Definition at line 9280 of file TH1.cxx.

SameLimitsAndNBins()

Bool_t TH1::SameLimitsAndNBins ( const TAxis &  axis1, const TAxis &  axis2  )

staticprotected

Same limits and bins.

Definition at line 5829 of file TH1.cxx.

SavePrimitive()

void TH1::SavePrimitive ( std::ostream &  out, Option_t *  option = ""  )

virtual

Save primitive as a C++ statement(s) on output stream out.

Reimplemented from TObject.

Reimplemented in TH1K, TH2Poly, TProfile, TProfile2D, and TProfile3D.

Definition at line 7122 of file TH1.cxx.

SavePrimitiveHelp()

void TH1::SavePrimitiveHelp ( std::ostream &  out, const char *  hname, Option_t *  option = ""  )

protectedvirtual

Helper function for the SavePrimitive functions from TH1 or classes derived from TH1, eg TProfile, TProfile2D.

Definition at line 7264 of file TH1.cxx.

Scale()

void TH1::Scale ( Double_t  c1 = 1, Option_t *  option = ""  )

virtual

Multiply this histogram by a constant c1.

this = c1*this

Note that both contents and errors (if any) are scaled. This function uses the services of TH1::Add

IMPORTANT NOTE: Sumw2() is called automatically when scaling. If you are not interested in the histogram statistics you can call Sumw2(kFALSE) or use the option "nosw2"

One can scale an histogram such that the bins integral is equal to the normalization parameter via TH1::Scale(Double_t norm), where norm is the desired normalization divided by the integral of the histogram.

If option contains "width" the bin contents and errors are divided by the bin width.

Reimplemented in TH2Poly, TProfile, TProfile2D, and TProfile3D.

Definition at line 6564 of file TH1.cxx.

SetAxisColor()

void TH1::SetAxisColor ( Color_t  color = 1, Option_t *  axis = "X"  )

virtual

Set color to draw the axis line and tick marks.

axis specifies which axis ("x","y","z"), default = "x" if axis="xyz" set all 3 axes

Definition at line 187 of file Haxis.cxx.

SetAxisRange()

void TH1::SetAxisRange ( Double_t  xmin, Double_t  xmax, Option_t *  axis = "X"  )

virtual

Set the "axis" range.

Definition at line 201 of file Haxis.cxx.

SetBarOffset()

void TH1::SetBarOffset ( Float_t  offset = 0.25 )

inlinevirtual

Set the bar offset as fraction of the bin width for drawing mode "B".

This shifts bars to the right on the x axis, and helps to draw bars next to each other.

See also

THistPainter, SetBarWidth()

Definition at line 359 of file TH1.h.

SetBarWidth()

void TH1::SetBarWidth ( Float_t  width = 0.5 )

inlinevirtual

Set the width of bars as fraction of the bin width for drawing mode "B".

This allows for making bars narrower than the bin width. With SetBarOffset(), this helps to draw multiple bars next to each other.

See also

THistPainter, SetBarOffset()

Definition at line 360 of file TH1.h.

SetBinContent() [1/3]

void TH1::SetBinContent ( Int_t  bin, Double_t  content  )

virtual

Set bin content see convention for numbering bins in TH1::GetBin In case the bin number is greater than the number of bins and the timedisplay option is set or CanExtendAllAxes(), the number of bins is automatically doubled to accommodate the new bin.

Reimplemented in TH2, TH2Poly, and TH3.

Definition at line 9062 of file TH1.cxx.

SetBinContent() [2/3]

virtual void TH1::SetBinContent ( Int_t  bin, Int_t  , Double_t  content  )

inlinevirtual

Reimplemented in TH3, TH2, and TH2Poly.

Definition at line 362 of file TH1.h.

SetBinContent() [3/3]

virtual void TH1::SetBinContent ( Int_t  bin, Int_t  , Int_t  , Double_t  content  )

inlinevirtual

Reimplemented in TH3, TH2, and TH2Poly.

Definition at line 363 of file TH1.h.

SetBinError() [1/3]

void TH1::SetBinError ( Int_t  bin, Double_t  error  )

virtual

Set the bin Error Note that this resets the bin eror option to be of Normal Type and for the non-empty bin the bin error is set by default to the square root of their content.

Note that in case the user sets after calling SetBinError explicitly a new bin content (e.g. using SetBinContent) he needs then to provide also the corresponding bin error (using SetBinError) since the bin error will not be recalculated after setting the content and a default error = 0 will be used for those bins.

See convention for numbering bins in TH1::GetBin

Reimplemented in TH2Poly.

Definition at line 9046 of file TH1.cxx.

SetBinError() [2/3]

void TH1::SetBinError ( Int_t  binx, Int_t  biny, Double_t  error  )

virtual

See convention for numbering bins in TH1::GetBin.

Reimplemented in TH2Poly.

Definition at line 9081 of file TH1.cxx.

SetBinError() [3/3]

void TH1::SetBinError ( Int_t  binx, Int_t  biny, Int_t  binz, Double_t  error  )

virtual

See convention for numbering bins in TH1::GetBin.

Reimplemented in TH2Poly.

Definition at line 9091 of file TH1.cxx.

SetBinErrorOption()

virtual void TH1::SetBinErrorOption ( EBinErrorOpt  type )

inlinevirtual

Definition at line 376 of file TH1.h.

SetBins() [1/6]

void TH1::SetBins ( Int_t  nx, const Double_t *  xBins  )

virtual

Redefine x axis parameters with variable bin sizes.

The X axis parameters are modified. The bins content array is resized if errors (Sumw2) the errors array is resized The previous bin contents are lost To change only the axis limits, see TAxis::SetRange xBins is supposed to be of length nx+1

Reimplemented in TProfile, TProfile2D, and TProfile3D.

Definition at line 8634 of file TH1.cxx.

SetBins() [2/6]

void TH1::SetBins ( Int_t  nx, const Double_t *  xBins, Int_t  ny, const Double_t *  yBins  )

virtual

Redefine x and y axis parameters with variable bin sizes.

The X and Y axis parameters are modified. The bins content array is resized if errors (Sumw2) the errors array is resized The previous bin contents are lost To change only the axis limits, see TAxis::SetRange xBins is supposed to be of length nx+1, yBins is supposed to be of length ny+1

Reimplemented in TProfile2D, TProfile, and TProfile3D.

Definition at line 8688 of file TH1.cxx.

SetBins() [3/6]

void TH1::SetBins ( Int_t  nx, const Double_t *  xBins, Int_t  ny, const Double_t *  yBins, Int_t  nz, const Double_t *  zBins  )

virtual

Redefine x, y and z axis parameters with variable bin sizes.

The X, Y and Z axis parameters are modified. The bins content array is resized if errors (Sumw2) the errors array is resized The previous bin contents are lost To change only the axis limits, see TAxis::SetRange xBins is supposed to be of length nx+1, yBins is supposed to be of length ny+1, zBins is supposed to be of length nz+1

Reimplemented in TProfile3D, TProfile, and TProfile2D.

Definition at line 8745 of file TH1.cxx.

SetBins() [4/6]

void TH1::SetBins ( Int_t  nx, Double_t  xmin, Double_t  xmax  )

virtual

Redefine x axis parameters.

The X axis parameters are modified. The bins content array is resized if errors (Sumw2) the errors array is resized The previous bin contents are lost To change only the axis limits, see TAxis::SetRange

Reimplemented in TProfile, TProfile2D, and TProfile3D.

Definition at line 8607 of file TH1.cxx.

SetBins() [5/6]

void TH1::SetBins ( Int_t  nx, Double_t  xmin, Double_t  xmax, Int_t  ny, Double_t  ymin, Double_t  ymax  )

virtual

Redefine x and y axis parameters.

The X and Y axis parameters are modified. The bins content array is resized if errors (Sumw2) the errors array is resized The previous bin contents are lost To change only the axis limits, see TAxis::SetRange

Reimplemented in TProfile2D, TProfile, and TProfile3D.

Definition at line 8660 of file TH1.cxx.

SetBins() [6/6]

void TH1::SetBins ( Int_t  nx, Double_t  xmin, Double_t  xmax, Int_t  ny, Double_t  ymin, Double_t  ymax, Int_t  nz, Double_t  zmin, Double_t  zmax  )

virtual

Redefine x, y and z axis parameters.

The X, Y and Z axis parameters are modified. The bins content array is resized if errors (Sumw2) the errors array is resized The previous bin contents are lost To change only the axis limits, see TAxis::SetRange

Reimplemented in TProfile3D, TProfile, and TProfile2D.

Definition at line 8715 of file TH1.cxx.

SetBinsLength()

virtual void TH1::SetBinsLength ( Int_t  = -1 )

inlinevirtual

Reimplemented in TH1C, TH1S, TH1I, TH1F, TH1D, TH2C, TH2S, TH2I, TH2F, TH2D, TH3C, TH3S, TH3I, TH3F, TH3D, TProfile, TProfile2D, and TProfile3D.

Definition at line 375 of file TH1.h.

SetBuffer()

void TH1::SetBuffer ( Int_t  buffersize, Option_t *  option = ""  )

virtual

Set the maximum number of entries to be kept in the buffer.

Reimplemented in TProfile3D, TProfile, and TProfile2D.

Definition at line 8306 of file TH1.cxx.

SetCanExtend()

UInt_t TH1::SetCanExtend ( UInt_t  extendBitMask )

virtual

Make the histogram axes extendable / not extendable according to the bit mask returns the previous bit mask specifying which axes are extendable.

Definition at line 6609 of file TH1.cxx.

SetCellContent()

virtual void TH1::SetCellContent ( Int_t  binx, Int_t  biny, Double_t  content  )

inlinevirtual

Definition at line 433 of file TH1.h.

SetCellError()

virtual void TH1::SetCellError ( Int_t  binx, Int_t  biny, Double_t  content  )

inlinevirtual

Definition at line 435 of file TH1.h.

SetContent()

void TH1::SetContent ( const Double_t *  content )

virtual

Replace bin contents by the contents of array content.

Definition at line 8246 of file TH1.cxx.

SetContour()

void TH1::SetContour ( Int_t  nlevels, const Double_t *  levels = 0  )

virtual

Set the number and values of contour levels.

By default the number of contour levels is set to 20. The contours values in the array "levels" should be specified in increasing order.

if argument levels = 0 or missing, equidistant contours are computed

Definition at line 8331 of file TH1.cxx.

SetContourLevel()

void TH1::SetContourLevel ( Int_t  level, Double_t  value  )

virtual

Set value for one contour level.

Definition at line 8370 of file TH1.cxx.

SetDefaultBufferSize()

void TH1::SetDefaultBufferSize ( Int_t  buffersize = 1000 )

static

Static function to set the default buffer size for automatic histograms.

When an histogram is created with one of its axis lower limit greater or equal to its upper limit, the function SetBuffer is automatically called with the default buffer size.

Definition at line 6653 of file TH1.cxx.

SetDefaultSumw2()

void TH1::SetDefaultSumw2 ( Bool_t  sumw2 = kTRUE )

static

When this static function is called with sumw2=kTRUE, all new histograms will automatically activate the storage of the sum of squares of errors, ie TH1::Sumw2 is automatically called.

Definition at line 6663 of file TH1.cxx.

SetDirectory()

void TH1::SetDirectory ( TDirectory *  dir )

virtual

By default when an histogram is created, it is added to the list of histogram objects in the current directory in memory.

Remove reference to this histogram from current directory and add reference to new directory dir. dir can be 0 in which case the histogram does not belong to any directory.

Note that the directory is not a real property of the histogram and it will not be copied when the histogram is copied or cloned. If the user wants to have the copied (cloned) histogram in the same directory, he needs to set again the directory using SetDirectory to the copied histograms

Definition at line 8777 of file TH1.cxx.

SetEntries()

virtual void TH1::SetEntries ( Double_t  n )

inlinevirtual

Definition at line 385 of file TH1.h.

SetError()

void TH1::SetError ( const Double_t *  error )

virtual

Replace bin errors by values in array error.

Definition at line 8791 of file TH1.cxx.

SetHighlight()

void TH1::SetHighlight ( Bool_t  set = kTRUE )

virtual

Set highlight (enable/disable) mode for the histogram by default highlight mode is disable.

Definition at line 4422 of file TH1.cxx.

SetLabelColor()

void TH1::SetLabelColor ( Color_t  color = 1, Option_t *  axis = "X"  )

virtual

Set axis labels color.

axis specifies which axis ("x","y","z"), default = "x" if axis="xyz" set all 3 axes

Definition at line 226 of file Haxis.cxx.

SetLabelFont()

void TH1::SetLabelFont ( Style_t  font = 62, Option_t *  axis = "X"  )

virtual

Set font number used to draw axis labels.

font : Text font code = 10*fontnumber + precision Font numbers must be between 1 and 14 precision = 1 fast hardware fonts (steps in the size) precision = 2 scalable and rotatable hardware fonts

The default font number is 62. axis specifies which axis ("x","y","z"), default = "x" if axis="xyz" set all 3 axes

Definition at line 249 of file Haxis.cxx.

SetLabelOffset()

void TH1::SetLabelOffset ( Float_t  offset = 0.005, Option_t *  axis = "X"  )

virtual

Set offset between axis and axis' labels.

The offset is expressed as a percent of the pad height. axis specifies which axis ("x","y","z"), default = "x" if axis="xyz" set all 3 axes

Definition at line 267 of file Haxis.cxx.

SetLabelSize()

void TH1::SetLabelSize ( Float_t  size = 0.02, Option_t *  axis = "X"  )

virtual

Set size of axis' labels.

The size is expressed as a percent of the pad height. axis specifies which axis ("x","y","z"), default = "x" if axis="xyz" set all 3 axes

Definition at line 285 of file Haxis.cxx.

SetMaximum()

virtual void TH1::SetMaximum ( Double_t  maximum = -1111 )

inlinevirtual

Definition at line 398 of file TH1.h.

SetMinimum()

virtual void TH1::SetMinimum ( Double_t  minimum = -1111 )

inlinevirtual

Definition at line 399 of file TH1.h.

SetName()

void TH1::SetName ( const char *  name )

virtual

Change the name of this histogram.

Reimplemented from TNamed.

Definition at line 8800 of file TH1.cxx.

SetNameTitle()

void TH1::SetNameTitle ( const char *  name, const char *  title  )

virtual

Change the name and title of this histogram.

Reimplemented from TNamed.

Definition at line 8814 of file TH1.cxx.

SetNdivisions()

void TH1::SetNdivisions ( Int_t  n = 510, Option_t *  axis = "X"  )

virtual

Set the number of divisions to draw an axis.

ndiv : Number of divisions.

 n = N1 + 100*N2 + 10000*N3
 N1=number of primary divisions.
 N2=number of secondary divisions.
 N3=number of 3rd divisions.
     e.g.:
     nndi=0 --> no tick marks.
     nndi=2 --> 2 divisions, one tick mark in the middle
                of the axis.

axis specifies which axis ("x","y","z"), default = "x" if axis="xyz" set all 3 axes

Definition at line 170 of file Haxis.cxx.

SetNormFactor()

virtual void TH1::SetNormFactor ( Double_t  factor = 1 )

inlinevirtual

Definition at line 404 of file TH1.h.

SetOption()

virtual void TH1::SetOption ( Option_t *  option = " " )

inlinevirtual

Definition at line 406 of file TH1.h.

SetStatOverflows()

void TH1::SetStatOverflows ( EStatOverflows  statOverflows )

inline

Definition at line 411 of file TH1.h.

SetStats()

void TH1::SetStats ( Bool_t  stats = kTRUE )

virtual

Set statistics option on/off.

By default, the statistics box is drawn. The paint options can be selected via gStyle->SetOptStats. This function sets/resets the kNoStats bit in the histogram object. It has priority over the Style option.

Definition at line 8830 of file TH1.cxx.

SetTickLength()

void TH1::SetTickLength ( Float_t  length = 0.02, Option_t *  axis = "X"  )

virtual

Set the axis' tick marks length.

axis specifies which axis ("x","y","z"), default = "x" if axis="xyz" set all 3 axes

Definition at line 302 of file Haxis.cxx.

SetTitle()

void TH1::SetTitle ( const char *  title )

virtual

See GetStatOverflows for more information.

Change (i.e.

set) the title

if title is in the form stringt;stringx;stringy;stringz the histogram title is set to stringt, the x axis title to stringx, the y axis title to stringy, and the z axis title to stringz.

To insert the character ; in one of the titles, one should use #; or #semicolon.

Reimplemented from TNamed.

Definition at line 6678 of file TH1.cxx.

SetTitleFont()

void TH1::SetTitleFont ( Style_t  font = 62, Option_t *  axis = "X"  )

virtual

Set the axis' title font.

• if axis =="x" set the X axis title font
• if axis =="y" set the Y axis title font
• if axis =="z" set the Z axis title font any other value of axis will set the pad title font

if axis="xyz" set all 3 axes

Definition at line 323 of file Haxis.cxx.

SetTitleOffset()

void TH1::SetTitleOffset ( Float_t  offset = 1, Option_t *  axis = "X"  )

virtual

Specify a parameter offset to control the distance between the axis and the axis' title.

• offset = 1 means : use the default distance
• offset = 1.2 means: the distance will be 1.2*(default distance)
• offset = 0.8 means: the distance will be 0.8*(default distance)

axis specifies which axis ("x","y","z"), default = "x" if axis="xyz" set all 3 axes

Definition at line 345 of file Haxis.cxx.

SetTitleSize()

void TH1::SetTitleSize ( Float_t  size = 0.02, Option_t *  axis = "X"  )

virtual

Set the axis' title size.

• if axis = "x" set the X axis title size
• if axis = "y" set the Y axis title size
• if axis = "z" set the Z axis title size

if axis ="xyz" set all 3 axes

Definition at line 365 of file Haxis.cxx.

SetXTitle()

virtual void TH1::SetXTitle ( const char *  title )

inlinevirtual

Definition at line 413 of file TH1.h.

SetYTitle()

virtual void TH1::SetYTitle ( const char *  title )

inlinevirtual

Definition at line 414 of file TH1.h.

SetZTitle()

virtual void TH1::SetZTitle ( const char *  title )

inlinevirtual

Definition at line 415 of file TH1.h.

ShowBackground()

TH1 * TH1::ShowBackground ( Int_t  niter = 20, Option_t *  option = "same"  )

virtual

This function calculates the background spectrum in this histogram.

The background is returned as a histogram.

Parameters

[in]	niter	number of iterations (default value = 2) Increasing niter make the result smoother and lower.
[in]	option	may contain one of the following options to set the direction parameter "BackDecreasingWindow". By default the direction is BackIncreasingWindow filterOrder-order of clipping filter (default "BackOrder2") possible values= "BackOrder4" "BackOrder6" "BackOrder8" "nosmoothing" - if selected, the background is not smoothed By default the background is smoothed. smoothWindow - width of smoothing window, (default is "BackSmoothing3") possible values= "BackSmoothing5" "BackSmoothing7" "BackSmoothing9" "BackSmoothing11" "BackSmoothing13" "BackSmoothing15" "nocompton" - if selected the estimation of Compton edge will be not be included (by default the compton estimation is set) "same" if this option is specified, the resulting background histogram is superimposed on the picture in the current pad. This option is given by default.

NOTE that the background is only evaluated in the current range of this histogram. i.e., if this has a bin range (set via h->GetXaxis()->SetRange(binmin, binmax), the returned histogram will be created with the same number of bins as this input histogram, but only bins from binmin to binmax will be filled with the estimated background.

Reimplemented in TH2.

Definition at line 9127 of file TH1.cxx.

ShowPeaks()

Int_t TH1::ShowPeaks ( Double_t  sigma = 2, Option_t *  option = "", Double_t  threshold = 0.05  )

virtual

Interface to TSpectrum::Search.

The function finds peaks in this histogram where the width is > sigma and the peak maximum greater than threshold*maximum bin content of this. For more details see TSpectrum::Search. Note the difference in the default value for option compared to TSpectrum::Search option="" by default (instead of "goff").

Reimplemented in TH2.

Definition at line 9142 of file TH1.cxx.

Smooth()

void TH1::Smooth ( Int_t  ntimes = 1, Option_t *  option = ""  )

virtual

Smooth bin contents of this histogram.

if option contains "R" smoothing is applied only to the bins defined in the X axis range (default is to smooth all bins) Bin contents are replaced by their smooth values. Errors (if any) are not modified. the smoothing procedure is repeated ntimes (default=1)

Reimplemented in TH2.

Definition at line 6845 of file TH1.cxx.

SmoothArray()

void TH1::SmoothArray ( Int_t  nn, Double_t *  xx, Int_t  ntimes = 1  )

static

Smooth array xx, translation of Hbook routine hsmoof.F based on algorithm 353QH twice presented by J.

Friedman in Proc.of the 1974 CERN School of Computing, Norway, 11-24 August, 1974.

Definition at line 6727 of file TH1.cxx.

StatOverflows()

void TH1::StatOverflows ( Bool_t  flag = kTRUE )

static

if flag=kTRUE, underflows and overflows are used by the Fill functions in the computation of statistics (mean value, StdDev).

By default, underflows or overflows are not used.

Definition at line 6891 of file TH1.cxx.

Sumw2()

void TH1::Sumw2 ( Bool_t  flag = kTRUE )

virtual

Create structure to store sum of squares of weights.

if histogram is already filled, the sum of squares of weights is filled with the existing bin contents

The error per bin will be computed as sqrt(sum of squares of weight) for each bin.

This function is automatically called when the histogram is created if the static function TH1::SetDefaultSumw2 has been called before. If flag = false the structure containing the sum of the square of weights is rest and it will be empty, but it is not deleted (i.e. GetSumw2()->fN = 0)

Reimplemented in TProfile, TProfile2D, and TProfile3D.

Definition at line 8860 of file TH1.cxx.

TransformHisto()

TH1 * TH1::TransformHisto ( TVirtualFFT *  fft, TH1 *  h_output, Option_t *  option  )

static

For a given transform (first parameter), fills the histogram (second parameter) with the transform output data, specified in the third parameter If the 2nd parameter h_output is empty, a new histogram (TH1D or TH2D) is created and the user is responsible for deleting it.

Available options:

• "RE" - real part of the output
• "IM" - imaginary part of the output
• "MAG" - magnitude of the output
• "PH" - phase of the output

Definition at line 9160 of file TH1.cxx.

UpdateBinContent()

void TH1::UpdateBinContent ( Int_t  bin, Double_t  content  )

protectedvirtual

Raw update of bin content on internal data structure see convention for numbering bins in TH1::GetBin.

Reimplemented in TH1C, TH1S, TH1I, TH1F, TH1D, TH2C, TH2S, TH2I, TH2F, TH2D, TH2Poly, TH3C, TH3S, TH3I, TH3F, and TH3D.

Definition at line 9290 of file TH1.cxx.

UseCurrentStyle()

void TH1::UseCurrentStyle ( )

virtual

Copy current attributes from/to current style.

Reimplemented from TObject.

Definition at line 7355 of file TH1.cxx.

Friends And Related Symbol Documentation

TH1Merger

friend class TH1Merger

friend

Definition at line 85 of file TH1.h.

Member Data Documentation

fBarOffset

Short_t TH1::fBarOffset

protected

(1000*offset) for bar charts or legos

Definition at line 92 of file TH1.h.

fBarWidth

Short_t TH1::fBarWidth

protected

(1000*width) for bar charts or legos

Definition at line 93 of file TH1.h.

fBinStatErrOpt

EBinErrorOpt TH1::fBinStatErrOpt

protected

option for bin statistical errors

Definition at line 112 of file TH1.h.

fBuffer

Double_t* TH1::fBuffer

protected

[fBufferSize] entry buffer

Definition at line 107 of file TH1.h.

fBufferSize

Int_t TH1::fBufferSize

protected

fBuffer size

Definition at line 106 of file TH1.h.

fContour

TArrayD TH1::fContour

protected

Array to display contour levels.

Definition at line 102 of file TH1.h.

fDimension

Int_t TH1::fDimension

protected

!Histogram dimension (1, 2 or 3 dim)

Definition at line 109 of file TH1.h.

fDirectory

TDirectory* TH1::fDirectory

protected

!Pointer to directory holding this histogram

Definition at line 108 of file TH1.h.

fEntries

Double_t TH1::fEntries

protected

Number of entries.

Definition at line 94 of file TH1.h.

fFunctions

TList* TH1::fFunctions

protected

->Pointer to list of functions (fits and user)

Definition at line 105 of file TH1.h.

fgAddDirectory

Bool_t TH1::fgAddDirectory = kTRUE

staticprotected

!flag to add histograms to the directory

Definition at line 115 of file TH1.h.

fgBufferSize

Int_t TH1::fgBufferSize = 1000

staticprotected

!default buffer size for automatic histograms

Definition at line 114 of file TH1.h.

fgDefaultSumw2

Bool_t TH1::fgDefaultSumw2 = kFALSE

staticprotected

!flag to call TH1::Sumw2 automatically at histogram creation time

Definition at line 117 of file TH1.h.

fgStatOverflows

Bool_t TH1::fgStatOverflows = kFALSE

staticprotected

!flag to use under/overflows in statistics

Definition at line 116 of file TH1.h.

fIntegral

Double_t* TH1::fIntegral

protected

!Integral of bins used by GetRandom

Definition at line 110 of file TH1.h.

fMaximum

Double_t TH1::fMaximum

protected

Maximum value for plotting.

Definition at line 99 of file TH1.h.

fMinimum

Double_t TH1::fMinimum

protected

Minimum value for plotting.

Definition at line 100 of file TH1.h.

fNcells

Int_t TH1::fNcells

protected

number of bins(1D), cells (2D) +U/Overflows

Definition at line 88 of file TH1.h.

fNormFactor

Double_t TH1::fNormFactor

protected

Normalization factor.

Definition at line 101 of file TH1.h.

fOption

TString TH1::fOption

protected

histogram options

Definition at line 104 of file TH1.h.

fPainter

TVirtualHistPainter* TH1::fPainter

protected

!pointer to histogram painter

Definition at line 111 of file TH1.h.

fStatOverflows

EStatOverflows TH1::fStatOverflows

protected

per object flag to use under/overflows in statistics

Definition at line 113 of file TH1.h.

fSumw2

TArrayD TH1::fSumw2

protected

Array of sum of squares of weights.

Definition at line 103 of file TH1.h.

fTsumw

Double_t TH1::fTsumw

protected

Total Sum of weights.

Definition at line 95 of file TH1.h.

fTsumw2

Double_t TH1::fTsumw2

protected

Total Sum of squares of weights.

Definition at line 96 of file TH1.h.

fTsumwx

Double_t TH1::fTsumwx

protected

Total Sum of weight*X.

Definition at line 97 of file TH1.h.

fTsumwx2

Double_t TH1::fTsumwx2

protected

Total Sum of weight*X*X.

Definition at line 98 of file TH1.h.

fXaxis

TAxis TH1::fXaxis

protected

X axis descriptor.

Definition at line 89 of file TH1.h.

fYaxis

TAxis TH1::fYaxis

protected

Y axis descriptor.

Definition at line 90 of file TH1.h.

fZaxis

TAxis TH1::fZaxis

protected

Z axis descriptor.

Definition at line 91 of file TH1.h.

Libraries for TH1:

---

The documentation for this class was generated from the following files:

• hist/hist/inc/TH1.h
• hist/hist/src/Haxis.cxx
• hist/hist/src/TH1.cxx