␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m
Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
All rights reserved, please read http://roofit.sourceforge.net/license.txt
RooCFunction1Binding<double,double>::erf[ function=TMath::Erf x=x ] = 0
RooCFunction3PdfBinding<double,double,double,double>::beta[ function=ROOT::Math::beta_pdf x=x2 a=a b=b ] = 0.934689
[#1] INFO:NumericIntegration -- RooRealIntegral::init(beta_Int[x2]) using numeric integrator RooIntegrator1D to calculate Int(x2)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(beta_Int[x2]) using numeric integrator RooIntegrator1D to calculate Int(x2)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(beta_Int[x2]) using numeric integrator RooIntegrator1D to calculate Int(x2)
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
**********
** 1 **SET PRINT 1
**********
**********
** 2 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 a 5.00000e+00 1.00000e+00 0.00000e+00 1.00000e+01
2 b 2.00000e+00 1.00000e+00 0.00000e+00 1.00000e+01
**********
** 3 **SET ERR 0.5
**********
**********
** 4 **SET PRINT 1
**********
**********
** 5 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 6 **MIGRAD 1000 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
FCN=-4851.7 FROM MIGRAD STATUS=INITIATE 10 CALLS 11 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a 5.00000e+00 1.00000e+00 2.01358e-01 -5.86406e+01
2 b 2.00000e+00 1.00000e+00 2.57889e-01 3.98974e+02
ERR DEF= 0.5
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=-4851.9 FROM MIGRAD STATUS=CONVERGED 39 CALLS 40 TOTAL
EDM=4.45664e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a 4.99036e+00 7.12139e-02 3.69873e-04 8.65175e-02
2 b 1.98812e+00 2.63908e-02 1.71677e-04 -1.47761e-01
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
5.072e-03 1.582e-03
1.582e-03 6.965e-04
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.84198 1.000 0.842
2 0.84198 0.842 1.000
**********
** 7 **SET ERR 0.5
**********
**********
** 8 **SET PRINT 1
**********
**********
** 9 **HESSE 1000
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=-4851.9 FROM HESSE STATUS=OK 10 CALLS 50 TOTAL
EDM=4.46009e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 a 4.99036e+00 7.12317e-02 7.39745e-05 -1.92762e-03
2 b 1.98812e+00 2.63974e-02 3.43355e-05 -6.46475e-01
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
5.074e-03 1.583e-03
1.583e-03 6.968e-04
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.84207 1.000 0.842
2 0.84207 0.842 1.000
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(beta_Int[x2]) using numeric integrator RooIntegrator1D to calculate Int(x2)
RooTFnBinding::fa1[ TFn={fa1=sin(x)/x} obs=(x3) ] = -0.0547936
void rf105_funcbinding()
{
RooPlot *frame1 =
x.frame(
Title(
"TMath::Erf bound as RooFit function"));
RooPlot *frame2 =
x2.frame(
Title(
"ROOT::Math::Beta bound as RooFit pdf"));
TF1 *fa1 =
new TF1(
"fa1",
"sin(x)/x", 0, 10);
TCanvas *
c =
new TCanvas(
"rf105_funcbinding",
"rf105_funcbinding", 1200, 400);
gPad->SetLeftMargin(0.15);
gPad->SetLeftMargin(0.15);
gPad->SetLeftMargin(0.15);
}
static const double x2[5]
static const double x3[11]
virtual void Print(Option_t *options=0) const
Print TNamed name and title.
virtual RooPlot * plotOn(RooPlot *frame, const RooCmdArg &arg1=RooCmdArg::none(), const RooCmdArg &arg2=RooCmdArg::none(), const RooCmdArg &arg3=RooCmdArg::none(), const RooCmdArg &arg4=RooCmdArg::none(), const RooCmdArg &arg5=RooCmdArg::none(), const RooCmdArg &arg6=RooCmdArg::none(), const RooCmdArg &arg7=RooCmdArg::none(), const RooCmdArg &arg8=RooCmdArg::none()) const
Calls RooPlot* plotOn(RooPlot* frame, const RooLinkedList& cmdList) const ;.
RooAbsReal is the common abstract base class for objects that represent a real value and implements f...
virtual RooPlot * plotOn(RooPlot *frame, const RooCmdArg &arg1=RooCmdArg(), const RooCmdArg &arg2=RooCmdArg(), const RooCmdArg &arg3=RooCmdArg(), const RooCmdArg &arg4=RooCmdArg(), const RooCmdArg &arg5=RooCmdArg(), const RooCmdArg &arg6=RooCmdArg(), const RooCmdArg &arg7=RooCmdArg(), const RooCmdArg &arg8=RooCmdArg(), const RooCmdArg &arg9=RooCmdArg(), const RooCmdArg &arg10=RooCmdArg()) const
Plot (project) PDF on specified frame.
RooDataSet is a container class to hold unbinned data.
A RooPlot is a plot frame and a container for graphics objects within that frame.
virtual void Draw(Option_t *options=0)
Draw this plot and all of the elements it contains.
RooRealVar represents a fundamental (non-derived) real valued object.
virtual void SetTitleOffset(Float_t offset=1)
Set distance between the axis and the axis title Offset is a correction factor with respect to the "s...
double beta_pdf(double x, double a, double b)
Probability density function of the beta distribution.
double beta(double x, double y)
Calculates the beta function.
Template specialisation used in RooAbsArg:
RooAbsPdf * bindPdf(const char *name, CFUNCD1D func, RooAbsReal &x)
RooAbsReal * bindFunction(const char *name, CFUNCD1D func, RooAbsReal &x)
Double_t Erf(Double_t x)
Computation of the error function erf(x).



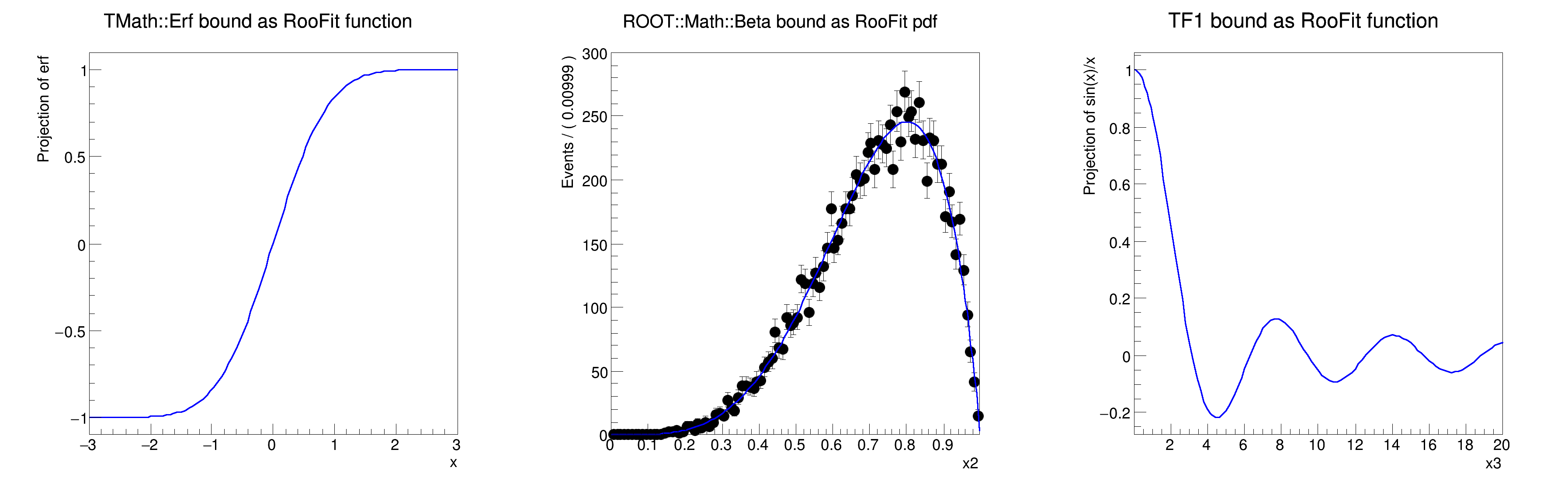
 Basic functionality: binding ROOT math functions as RooFit functions and pdfs
Basic functionality: binding ROOT math functions as RooFit functions and pdfs