mpc = par[1] - mpshift * par[0];
xlow = x[0] - sc * par[3];
xupp = x[0] + sc * par[3];
step = (xupp-xlow) / np;
for(i=1.0; i<=np/2; i++) {
xx = xlow + (i-.5) * step;
xx = xupp - (i-.5) * step;
}
return (par[2] * step * sum * invsq2pi / par[3]);
}
{
sprintf(FunName,
"Fitfcn_%s",his->
GetName());
TF1 *ffitold = (
TF1*)
gROOT->GetListOfFunctions()->FindObject(FunName);
if (ffitold) delete ffitold;
TF1 *ffit =
new TF1(FunName,langaufun,fitrange[0],fitrange[1],4);
for (i=0; i<4; i++) {
}
for (i=0; i<4; i++) {
}
return (ffit);
}
p = params[1] - 0.1 * params[0];
step = 0.05 * params[0];
lold = -2.0;
l = -1.0;
while ( (l != lold) && (i < MAXCALLS) ) {
i++;
x = p + step;
l = langaufun(&x,params);
if (l < lold)
step = -step/10;
p += step;
}
if (i == MAXCALLS)
return (-1);
fy = l/2;
p = maxx + params[0];
step = params[0];
lold = -2.0;
l = -1e300;
i = 0;
while ( (l != lold) && (i < MAXCALLS) ) {
i++;
x = p + step;
if (l > lold)
step = -step/10;
p += step;
}
if (i == MAXCALLS)
return (-2);
p = maxx - 0.5 * params[0];
step = -params[0];
lold = -2.0;
l = -1e300;
i = 0;
while ( (l != lold) && (i < MAXCALLS) ) {
i++;
x = p + step;
if (l > lold)
step = -step/10;
p += step;
}
if (i == MAXCALLS)
return (-3);
FWHM = fxr - fxl;
return (0);
}
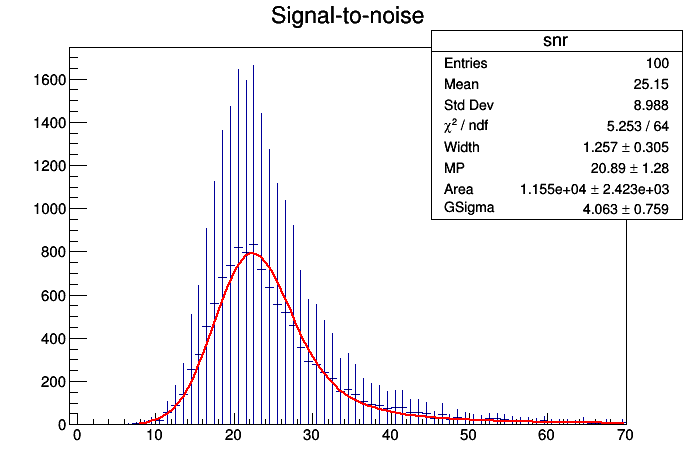
void langaus() {
Int_t data[100] = {0,0,0,0,0,0,2,6,11,18,18,55,90,141,255,323,454,563,681,
737,821,796,832,720,637,558,519,460,357,291,279,241,212,
153,164,139,106,95,91,76,80,80,59,58,51,30,49,23,35,28,23,
22,27,27,24,20,16,17,14,20,12,12,13,10,17,7,6,12,6,12,4,
9,9,10,3,4,5,2,4,1,5,5,1,7,1,6,3,3,3,4,5,4,4,2,2,7,2,4};
TH1F *hSNR =
new TH1F(
"snr",
"Signal-to-noise",400,0,400);
for (
Int_t i=0; i<100; i++) hSNR->
Fill(i,data[i]);
printf("Fitting...\n");
Double_t sv[4], pllo[4], plhi[4], fp[4], fpe[4];
pllo[0]=0.5; pllo[1]=5.0; pllo[2]=1.0; pllo[3]=0.4;
plhi[0]=5.0; plhi[1]=50.0; plhi[2]=1000000.0; plhi[3]=5.0;
sv[0]=1.8; sv[1]=20.0; sv[2]=50000.0; sv[3]=3.0;
TF1 *fitsnr = langaufit(hSNR,fr,sv,pllo,plhi,fp,fpe,&chisqr,&ndf);
langaupro(fp,SNRPeak,SNRFWHM);
printf("Fitting done\nPlotting results...\n");
}



 Convoluted Landau and Gaussian Fitting Function (using ROOT's Landau and Gauss functions)
Convoluted Landau and Gaussian Fitting Function (using ROOT's Landau and Gauss functions)