Example describing the usage of different kinds of Associate Legendre Polynomials To execute the macro type in:
Example describing the usage of different kinds of Associate Legendre Polynomials To execute the macro type in:
root[0] .x LegendreAssoc.C
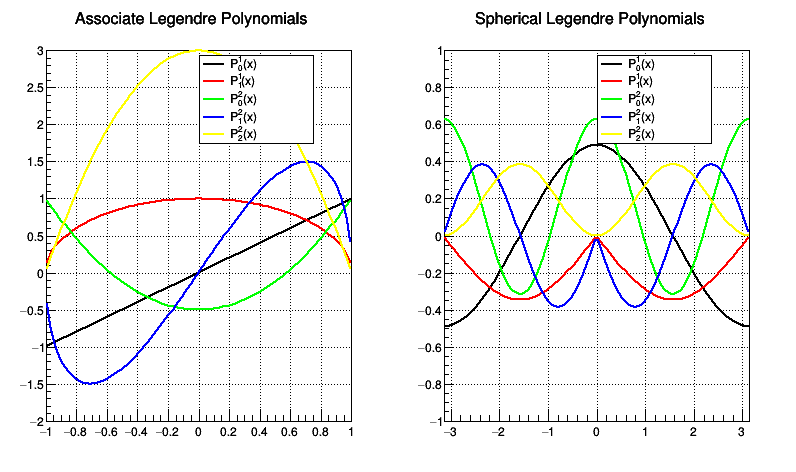
It draws common graphs for first 5 Associate Legendre Polynomials and Spherical Associate Legendre Polynomials Their integrals on the range [-1, 1] are calculated
Processing /mnt/build/workspace/root-makedoc-v612/rootspi/rdoc/src/v6-12-00-patches/tutorials/math/LegendreAssoc.C...
Drawing associate Legendre Polynomials..
Calculating integrals of Associate Legendre Polynomials on [-1, 1]
Integral [-1,1] for Associated Legendre Polynomial of Degree 0 = 0
Integral [-1,1] for Associated Legendre Polynomial of Degree 1 = 1.5708
Integral [-1,1] for Associated Legendre Polynomial of Degree 2 = 5.55112e-17
Integral [-1,1] for Associated Legendre Polynomial of Degree 3 = 0
Integral [-1,1] for Associated Legendre Polynomial of Degree 4 = 4
#include <cmath>
void LegendreAssoc()
{
std::cout <<"Drawing associate Legendre Polynomials.." << std::endl;
TCanvas *Canvas =
new TCanvas(
"DistCanvas",
"Associate Legendre polynomials", 10, 10, 800, 500);
L[0]=
new TF1(
"L_0",
"ROOT::Math::assoc_legendre(1, 0,x)", -1, 1);
L[1]=
new TF1(
"L_1",
"ROOT::Math::assoc_legendre(1, 1,x)", -1, 1);
L[2]=
new TF1(
"L_2",
"ROOT::Math::assoc_legendre(2, 0,x)", -1, 1);
L[3]=
new TF1(
"L_3",
"ROOT::Math::assoc_legendre(2, 1,x)", -1, 1);
L[4]=
new TF1(
"L_4",
"ROOT::Math::assoc_legendre(2, 2,x)", -1, 1);
L[0]->
SetTitle(
"Associate Legendre Polynomials");
for (int nu = 0; nu < 5; nu++) {
}
leg1->
AddEntry(L[0]->DrawCopy(),
" P^{1}_{0}(x)",
"l");
leg1->
AddEntry(L[1]->DrawCopy(
"same"),
" P^{1}_{1}(x)",
"l");
leg1->
AddEntry(L[2]->DrawCopy(
"same"),
" P^{2}_{0}(x)",
"l");
leg1->
AddEntry(L[3]->DrawCopy(
"same"),
" P^{2}_{1}(x)",
"l");
leg1->
AddEntry(L[4]->DrawCopy(
"same"),
" P^{2}_{2}(x)",
"l");
SL[0]->
SetTitle(
"Spherical Legendre Polynomials");
for (int nu = 0; nu < 5; nu++) {
}
leg2->
AddEntry(SL[0]->DrawCopy(),
" P^{1}_{0}(x)",
"l");
leg2->
AddEntry(SL[1]->DrawCopy(
"same"),
" P^{1}_{1}(x)",
"l");
leg2->
AddEntry(SL[2]->DrawCopy(
"same"),
" P^{2}_{0}(x)",
"l");
leg2->
AddEntry(SL[3]->DrawCopy(
"same"),
" P^{2}_{1}(x)",
"l");
leg2->
AddEntry(SL[4]->DrawCopy(
"same"),
" P^{2}_{2}(x)",
"l");
std::cout << "Calculating integrals of Associate Legendre Polynomials on [-1, 1]" << std::endl;
double integral[5];
for (int nu = 0; nu < 5; nu++) {
integral[nu] = L[nu]->
Integral(-1.0, 1.0);
std::cout <<"Integral [-1,1] for Associated Legendre Polynomial of Degree " << nu << "\t = \t" << integral[nu] << std::endl;
}
}
- Author
- Magdalena Slawinska
Definition in file LegendreAssoc.C.



 Example describing the usage of different kinds of Associate Legendre Polynomials To execute the macro type in:
Example describing the usage of different kinds of Associate Legendre Polynomials To execute the macro type in: