Detailed Description

Convolution in cyclical angular observables theta, and construction of p.d.f in terms of transformed angular coordinates, e.g.

cos(theta), the convolution is performed in theta rather than cos(theta)

(require ROOT to be compiled with –enable-fftw3)

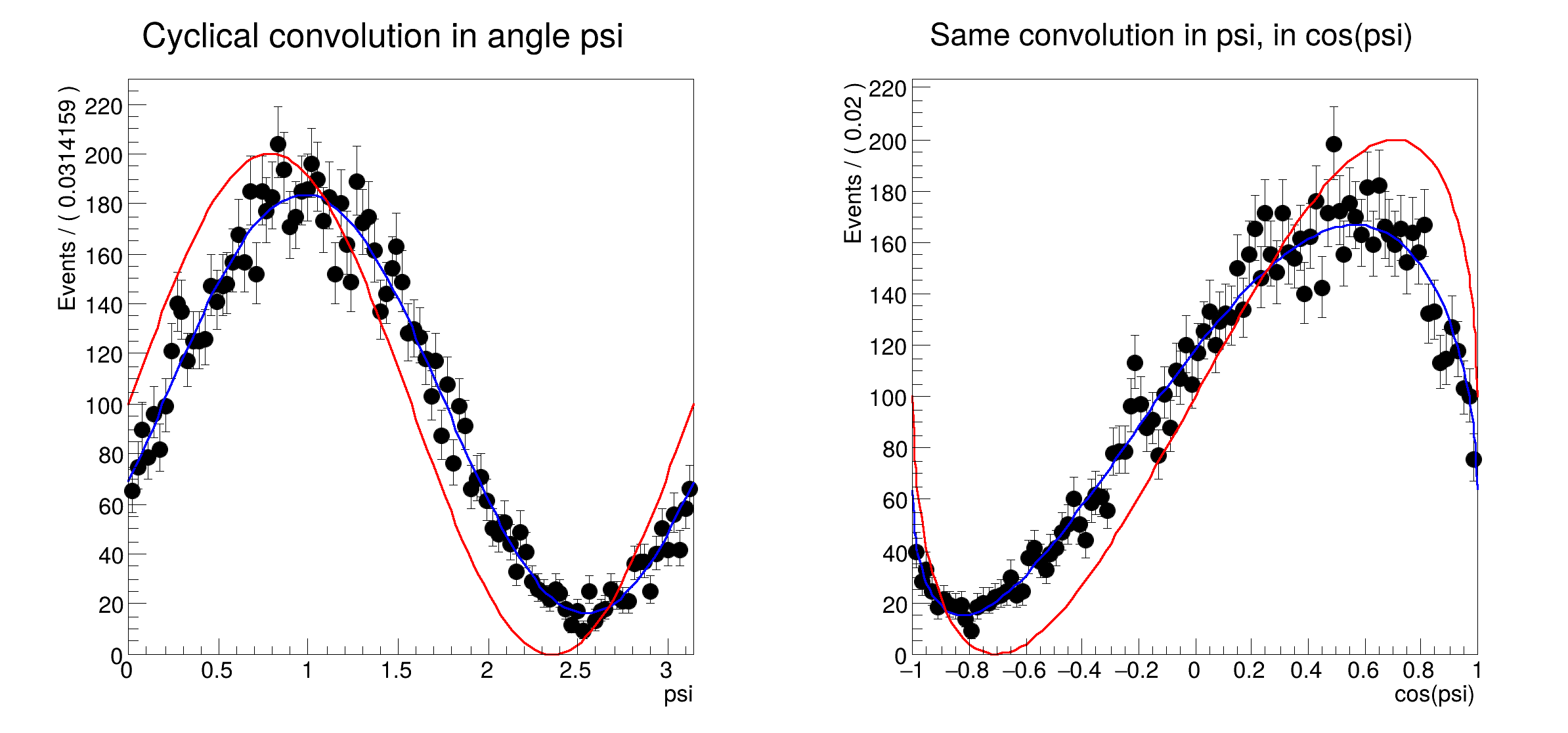
pdf(theta) = ROOT.T(theta) (x) gauss(theta) pdf(cosTheta) = ROOT.T(acos(cosTheta)) (x) gauss(acos(cosTheta))

 
import ROOT
 
# Set up component pdfs
# ---------------------------------------
 
# Define angle psi
psi = ROOT.RooRealVar("psi", "psi", 0, 3.14159268)
 
# Define physics p.d.f T(psi)
Tpsi = ROOT.RooGenericPdf("Tpsi", "1+sin(2*@0)", [psi])
 
# Define resolution R(psi)
gbias = ROOT.RooRealVar("gbias", "gbias", 0.2, 0.0, 1)
greso = ROOT.RooRealVar("greso", "greso", 0.3, 0.1, 1.0)
Rpsi = ROOT.RooGaussian("Rpsi", "Rpsi", psi, gbias, greso)
 
# Define cos(psi) and function psif that calculates psi from cos(psi)
cpsi = ROOT.RooRealVar("cpsi", "cos(psi)", -1, 1)
psif = ROOT.RooFormulaVar("psif", "acos(cpsi)", [cpsi])
 
# Define physics p.d.f. also as function of cos(psi): T(psif(cpsi)) = T(cpsi)
Tcpsi = ROOT.RooGenericPdf("T", "1+sin(2*@0)", [psif])
 
# Construct convolution pdf in psi
# --------------------------------------------------------------
 
# Define convoluted p.d.f. as function of psi: M=[T(x)R](psi) = M(psi)
Mpsi = ROOT.RooFFTConvPdf("Mf", "Mf", psi, Tpsi, Rpsi)
 
# Set the buffer fraction to zero to obtain a ROOT.True cyclical
# convolution
Mpsi.setBufferFraction(0)
 
# Sample, fit and plot convoluted pdf (psi)
# --------------------------------------------------------------------------------
 
# Generate some events in observable psi
data_psi = Mpsi.generate({psi}, 10000)
 
# Fit convoluted model as function of angle psi
Mpsi.fitTo(data_psi, PrintLevel=-1)
 
# Plot cos(psi) frame with Mf(cpsi)
frame1 = psi.frame(Title="Cyclical convolution in angle psi")
data_psi.plotOn(frame1)
Mpsi.plotOn(frame1)
 
# Overlay comparison to unsmeared physics p.d.f ROOT.T(psi)
Tpsi.plotOn(frame1, LineColor="r")
 
# Construct convolution pdf in cos(psi)
# --------------------------------------------------------------------------
 
# Define convoluted p.d.f. as function of cos(psi): M=[T(x)R](psif cpsi)) = M(cpsi:
#
# Need to give both observable psi here (for definition of convolution)
# and function psif here (for definition of observables, in cpsi)
Mcpsi = ROOT.RooFFTConvPdf("Mf", "Mf", psif, psi, Tpsi, Rpsi)
 
# Set the buffer fraction to zero to obtain a ROOT.True cyclical
# convolution
Mcpsi.setBufferFraction(0)
 
# Sample, fit and plot convoluted pdf (cospsi)
# --------------------------------------------------------------------------------
 
# Generate some events
data_cpsi = Mcpsi.generate({cpsi}, 10000)
 
# set psi constant to exclude to be a parameter of the fit
psi.setConstant(True)
 
# Fit convoluted model as function of cos(psi)
Mcpsi.fitTo(data_cpsi, PrintLevel=-1)
 
# Plot cos(psi) frame with Mf(cpsi)
frame2 = cpsi.frame(Title="Same convolution in psi, in cos(psi)")
data_cpsi.plotOn(frame2)
Mcpsi.plotOn(frame2)
 
# Overlay comparison to unsmeared physics p.d.f ROOT.Tf(cpsi)
Tcpsi.plotOn(frame2, LineColor="r")
 
# Draw frame on canvas
c = ROOT.TCanvas("rf210_angularconv", "rf210_angularconv", 800, 400)
c.Divide(2)
c.cd(1)
ROOT.gPad.SetLeftMargin(0.15)
frame1.GetYaxis().SetTitleOffset(1.4)
frame1.Draw()
c.cd(2)
ROOT.gPad.SetLeftMargin(0.15)
frame2.GetYaxis().SetTitleOffset(1.4)
frame2.Draw()
 
c.SaveAs("rf210_angularconv.png")

[#1] INFO:Caching -- Changing internal binning of variable 'psi' in FFT 'Mf' from 100 to 930 to improve the precision of the numerical FFT. This can be done manually by setting an additional binning named 'cache'.
[#1] INFO:Eval -- RooRealVar::setRange(psi) new range named 'refrange_fft_Mf' created with bounds [0,3.14159]
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_Int[psi]) using numeric integrator RooIntegrator1D to calculate Int(psi)
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55638e539780 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[psi]_NORM_psi for nset (psi) with code 0
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55638e729aa0 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[psi]_NORM_psi for nset (psi) with code 0 from preexisting content.
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55638e9e3ce0 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[psi]_NORM_psi for nset (psi) with code 0 from preexisting content.
[#1] INFO:Fitting -- RooAbsPdf::fitTo(Mf_over_Mf_Int[psi]) fixing normalization set for coefficient determination to observables in data
[#1] INFO:Fitting -- using generic CPU library compiled with no vectorizations
[#1] INFO:Fitting -- Creation of NLL object took 1.11386 ms
[#1] INFO:Fitting -- RooAddition::defaultErrorLevel(nll_Mf_over_Mf_Int[psi]_MfData) Summation contains a RooNLLVar, using its error level
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: activating const optimization
[#1] INFO:Minimization -- [fitFCN] No discrete parameters, performing continuous minimization only
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55638ea4a310 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[psi] for nset () with code 1 from preexisting content.
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_Int[psi]) using numeric integrator RooIntegrator1D to calculate Int(psi)
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_Int[psi]) using numeric integrator RooIntegrator1D to calculate Int(psi)
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55638eb9b1b0 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[psi]_NORM_psi for nset (psi) with code 0
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_Int[psi]) using numeric integrator RooIntegrator1D to calculate Int(psi)
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55638ec99430 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[cpsi]_NORM_cpsi for nset (cpsi) with code 0 from preexisting content.
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_CONV_Rpsi_CACHE_Obs[cpsi]_NORM_cpsi_Int[cpsi]) using numeric integrator RooIntegrator1D to calculate Int(cpsi)
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55638ec992c0 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[cpsi]_NORM_cpsi for nset (cpsi) with code 0 from preexisting content.
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_CONV_Rpsi_CACHE_Obs[cpsi]_NORM_cpsi_Int[cpsi]) using numeric integrator RooIntegrator1D to calculate Int(cpsi)
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55638ec365b0 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[cpsi]_NORM_cpsi for nset (cpsi) with code 0 from preexisting content.
[#1] INFO:Fitting -- RooAbsPdf::fitTo(Mf_over_Mf_Int[cpsi]) fixing normalization set for coefficient determination to observables in data
[#1] INFO:Fitting -- Creation of NLL object took 448.972 μs
[#1] INFO:Fitting -- RooAddition::defaultErrorLevel(nll_Mf_over_Mf_Int[cpsi]_MfData) Summation contains a RooNLLVar, using its error level
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: activating const optimization
[#1] INFO:Minimization -- [fitFCN] No discrete parameters, performing continuous minimization only
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55638ec9d8b0 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[cpsi] for nset () with code 1 from preexisting content.
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Mf_Int[cpsi]) using numeric integrator RooIntegrator1D to calculate Int(cpsi)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_Int[psi]) using numeric integrator RooIntegrator1D to calculate Int(psi)
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_Int[psi]) using numeric integrator RooIntegrator1D to calculate Int(psi)
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55638ec9d8b0 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[cpsi]_NORM_cpsi for nset (cpsi) with code 0
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_CONV_Rpsi_CACHE_Obs[cpsi]_NORM_cpsi_Int[cpsi]) using numeric integrator RooIntegrator1D to calculate Int(cpsi)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(T_Int[cpsi]) using numeric integrator RooIntegrator1D to calculate Int(cpsi)

Date: February 2018

Authors: Clemens Lange, Wouter Verkerke (C version)

Definition in file rf210_angularconv.py.