 |
ROOT 6.07/09 Reference Guide |
 |
ROOT 6.07/09 Reference Guide |
Multidimensional Fits in ROOT.
A common problem encountered in different fields of applied science is to find an expression for one physical quantity in terms of several others, which are directly measurable.
An example in high energy physics is the evaluation of the momentum of a charged particle from the observation of its trajectory in a magnetic field. The problem is to relate the momentum of the particle to the observations, which may consists of positional measurements at intervals along the particle trajectory.
The exact functional relationship between the measured quantities (e.g., the space-points) and the dependent quantity (e.g., the momentum) is in general not known, but one possible way of solving the problem, is to find an expression which reliably approximates the dependence of the momentum on the observations.
This explicit function of the observations can be obtained by a least squares fitting procedure applied to a representative sample of the data, for which the dependent quantity (e.g., momentum) and the independent observations are known. The function can then be used to compute the quantity of interest for new observations of the independent variables.
This class TMultiDimFit implements such a procedure in ROOT. It is largely based on the CERNLIB MUDIFI package 2. Though the basic concepts are still sound, and therefore kept, a few implementation details have changed, and this class can take advantage of MINUIT 4 to improve the errors of the fitting, thanks to the class TMinuit.
In 5 and 6 H. Wind demonstrates the utility of this procedure in the context of tracking, magnetic field parameterisation, and so on. The outline of the method used in this class is based on Winds discussion, and I refer these two excellents text for more information.
And example of usage is given in multidimfit.C.
Let \( D \) by the dependent quantity of interest, which depends smoothly on the observable quantities \( x_1, \ldots, x_N \) which we'll denote by \(\mathbf{x}\). Given a training sample of \( M\) tuples of the form, (TMultiDimFit::AddRow)
\[ \left(\mathbf{x}_j, D_j, E_j\right)\quad, \]
where \(\mathbf{x}_j = (x_{1,j},\ldots,x_{N,j})\) are \( N\) independent variables, \( D_j\) is the known, quantity dependent at \(\mathbf{x}_j\) and \( E_j\) is the square error in \( D_j\), the class will try to find the parameterization
\[ D_p(\mathbf{x}) = \sum_{l=1}^{L} c_l \prod_{i=1}^{N} p_{li}\left(x_i\right) = \sum_{l=1}^{L} c_l F_l(\mathbf{x}) \]
such that
\[ S \equiv \sum_{j=1}^{M} \left(D_j - D_p\left(\mathbf{x}_j\right)\right)^2 \]
is minimal. Here \(p_{li}(x_i)\) are monomials, or Chebyshev or Legendre polynomials, labelled \(l = 1, \ldots, L\), in each variable \( x_i\), \( i=1, \ldots, N\).
So what TMultiDimFit does, is to determine the number of terms \( L\), and then \( L\) terms (or functions) \( F_l\), and the \( L\) coefficients \( c_l\), so that \( S\) is minimal (TMultiDimFit::FindParameterization).
Of course it's more than a little unlikely that \( S\) will ever become exact zero as a result of the procedure outlined below. Therefore, the user is asked to provide a minimum relative error \( \epsilon\) (TMultiDimFit::SetMinRelativeError), and \( S\) will be considered minimized when
\[ R = \frac{S}{\sum_{j=1}^M D_j^2} < \epsilon \]
Optionally, the user may impose a functional expression by specifying the powers of each variable in \( L\) specified functions \( F_1, \ldots,F_L\) (TMultiDimFit::SetPowers). In that case, only the coefficients \( c_l\) is calculated by the class.
As always when dealing with fits, there's a real chance of over fitting. As is well-known, it's always possible to fit an \( N-1\) polynomial in \( x\) to \( N\) points \( (x,y)\) with \(\chi^2 = 0\), but the polynomial is not likely to fit new data at all 1. Therefore, the user is asked to provide an upper limit, \( L_{max}\) to the number of terms in \( D_p\) (TMultiDimFit::SetMaxTerms).
However, since there's an infinite number of \( F_l\) to choose from, the user is asked to give the maximum power. \( P_{max,i}\), of each variable \( x_i\) to be considered in the minimization of \( S\) (TMultiDimFit::SetMaxPowers).
One way of obtaining values for the maximum power in variable \( i\), is to perform a regular fit to the dependent quantity \( D\), using a polynomial only in \( x_i\). The maximum power is \( P_{max,i}\) is then the power that does not significantly improve the one-dimensional least-square fit over \( x_i\) to \( D\) 5.
There are still a huge amount of possible choices for \( F_l\); in fact there are \(\prod_{i=1}^{N} (P_{max,i} + 1)\) possible choices. Obviously we need to limit this. To this end, the user is asked to set a power control limit, \( Q\) (TMultiDimFit::SetPowerLimit), and a function \( F_l\) is only accepted if
\[ Q_l = \sum_{i=1}^{N} \frac{P_{li}}{P_{max,i}} < Q \]
where \( P_{li}\) is the leading power of variable \( x_i\) in function \( F_l\) (TMultiDimFit::MakeCandidates). So the number of functions increase with \( Q\) (1, 2 is fine, 5 is way out).
To further reduce the number of functions in the final expression, only those functions that significantly reduce \( S\) is chosen. What `significant' means, is chosen by the user, and will be discussed below (see 2.3).
The functions \( F_l\) are generally not orthogonal, which means one will have to evaluate all possible \( F_l\)'s over all data-points before finding the most significant 1. We can, however, do better then that. By applying the modified Gram-Schmidt orthogonalisation algorithm [5] [3] to the functions \( F_l\), we can evaluate the contribution to the reduction of \( S\) from each function in turn, and we may delay the actual inversion of the curvature-matrix (TMultiDimFit::MakeGramSchmidt).
So we are let to consider an \( M\times L\) matrix \(\mathsf{F}\), an element of which is given by
\[ f_{jl} = F_j\left(x_{1j} , x_{2j}, \ldots, x_{Nj}\right) = F_l(\mathbf{x}_j)\, \quad\mbox{with}~j=1,2,\ldots,M, \]
where \( j\) labels the \( M\) rows in the training sample and \( l\) labels \( L\) functions of \( N\) variables, and \( L \leq M\). That is, \( f_{jl}\) is the term (or function) numbered \( l\) evaluated at the data point \( j\). We have to normalise \(\mathbf{x}_j\) to \( [-1,1]\) for this to succeed [5] (TMultiDimFit::MakeNormalized). We then define a matrix \(\mathsf{W}\) of which the columns \(\mathbf{w}_j\) are given by
\begin{eqnarray*} \mathbf{w}_1 &=& \mathbf{f}_1 = F_1\left(\mathbf x_1\right)\\ \mathbf{w}_l &=& \mathbf{f}_l - \sum^{l-1}_{k=1} \frac{\mathbf{f}_l \bullet \mathbf{w}_k}{\mathbf{w}_k^2}\mathbf{w}_k\,. \end{eqnarray*}
and \(\mathbf{w}_{l}\) is the component of \(\mathbf{f}_{l} \) orthogonal to \(\mathbf{w}_{1}, \ldots, \mathbf{w}_{l-1}\). Hence we obtain [3],
\[ \mathbf{w}_k\bullet\mathbf{w}_l = 0\quad\mbox{if}~k \neq l\quad. \]
We now take as a new model \(\mathsf{W}\mathbf{a}\). We thus want to minimize
\[ S\equiv \left(\mathbf{D} - \mathsf{W}\mathbf{a}\right)^2\quad, \]
where \(\mathbf{D} = \left(D_1,\ldots,D_M\right)\) is a vector of the dependent quantity in the sample. Differentiation with respect to \( a_j\) gives, using 6,
\[ \mathbf{D}\bullet\mathbf{w}_l - a_l\mathbf{w}_l^2 = 0 \]
or
\[ a_l = \frac{\mathbf{D}_l\bullet\mathbf{w}_l}{\mathbf{w}_l^2} \]
Let \( S_j\) be the sum of squares of residuals when taking \( j\) functions into account. Then
\[ S_l = \left[\mathbf{D} - \sum^l_{k=1} a_k\mathbf{w}_k\right]^2 = \mathbf{D}^2 - 2\mathbf{D} \sum^l_{k=1} a_k\mathbf{w}_k + \sum^l_{k=1} a_k^2\mathbf{w}_k^2 \]
Using 9, we see that
\begin{eqnarray*} S_l &=& \mathbf{D}^2 - 2 \sum^l_{k=1} a_k^2\mathbf{w}_k^2 + \sum^j_{k=1} a_k^2\mathbf{w}_k^2\nonumber\\ &=& \mathbf{D}^2 - \sum^l_{k=1} a_k^2\mathbf{w}_k^2\nonumber\\ &=& \mathbf{D}^2 - \sum^l_{k=1} \frac{\left(\mathbf D\bullet \mathbf w_k\right)}{\mathbf w_k^2} \end{eqnarray*}
So for each new function \( F_l\) included in the model, we get a reduction of the sum of squares of residuals of \(a_l^2\mathbf{w}_l^2\), where \(\mathbf{w}_l\) is given by 4 and \( a_l\) by 9. Thus, using the Gram-Schmidt orthogonalisation, we can decide if we want to include this function in the final model, before* the matrix inversion.
Supposing that \( L-1\) steps of the procedure have been performed, the problem now is to consider the \(L^{\mbox{th}}\) function.
The sum of squares of residuals can be written as
\[ S_L = \textbf{D}^T\bullet\textbf{D} - \sum^L_{l=1}a^2_l\left(\textbf{w}_l^T\bullet\textbf{w}_l\right) \]
where the relation 9 have been taken into account. The contribution of the \(L^{\mbox{th}}\) function to the reduction of S, is given by
\[ \Delta S_L = a^2_L\left(\textbf{w}_L^T\bullet\textbf{w}_L\right) \]
Two test are now applied to decide whether this \(L^{\mbox{th}}\) function is to be included in the final expression, or not.
Denoting by \( H_{L-1}\) the subspace spanned by \(\textbf{w}_1,\ldots,\textbf{w}_{L-1}\) the function ${w}_L$ is by construction (see 4) the projection of the function \( F_L\) onto the direction perpendicular to \( H_{L-1}\). Now, if the length of \(\textbf{w}_L\) (given by \(\textbf{w}_L\bullet\textbf{w}_L\)) is very small compared to the length of \(\textbf{f}_L\) this new function can not contribute much to the reduction of the sum of squares of residuals. The test consists then in calculating the angle \( \theta \) between the two vectors \(\textbf{w}_L\) \( \textbf {f}_L\) (see also figure 1) and requiring that it's greater* then a threshold value which the user must set (TMultiDimFit::SetMinAngle).
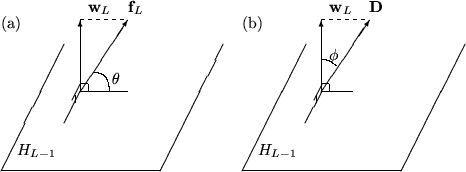
Let \(\textbf{D}\) be the data vector to be fitted. As illustrated in figure 1, the \(L^{\mbox{th}}\) function \(\textbf{w}_L\) will contribute significantly to the reduction of \( S\), if the angle \(\phi^\prime\) between \(\textbf{w}_L\) and \(\textbf{D}\) is smaller than an upper limit \( \phi \), defined by the user (MultiDimFit::SetMaxAngle)
However, the method automatically readjusts the value of this angle while fitting is in progress, in order to make the selection criteria less and less difficult to be fulfilled. The result is that the functions contributing most to the reduction of \( S\) are chosen first (TMultiDimFit::TestFunction).
In case \( \phi \) isn't defined, an alternative method of performing this second test is used: The \(L^{\mbox{th}}\) function \(\textbf{f}_L\) is accepted if (refer also to equation (13))
\[ \Delta S_L > \frac{S_{L-1}}{L_{max}-L} \]
where \( S_{L-1}\) is the sum of the \( L-1\) first residuals from the \( L-1\) functions previously accepted; and \( L_{max}\) is the total number of functions allowed in the final expression of the fit (defined by user).
From this we see, that by restricting \( L_{max}\) – the number of terms in the final model – the fit is more difficult to perform, since the above selection criteria is more limiting.
The more coefficients we evaluate, the more the sum of squares of residuals \( S\) will be reduced. We can evaluate \( S\) before inverting \(\mathsf{B}\) as shown below.
Having found a parameterization, that is the \( F_l\)'s and \( L\), that minimizes \( S\), we still need to determine the coefficients \( c_l\). However, it's a feature of how we choose the significant functions, that the evaluation of the \( c_l\)'s becomes trivial 5. To derive \(\mathbf{c}\), we first note that equation (4) can be written as
\[ \mathsf{F} = \mathsf{W}\mathsf{B} \]
where
\begin{eqnarray*} b_{ij} = \frac{\mathbf{f}_j \bullet \mathbf{w}_i}{\mathbf{w}_i^2} & \mbox{if} & i < j\\ 1 & \mbox{if} & i = j\\ 0 & \mbox{if} & i > j \end{eqnarray*}
Consequently, \(\mathsf{B}\) is an upper triangle matrix, which can be readily inverted. So we now evaluate
\[ \mathsf{F}\mathsf{B}^{-1} = \mathsf{W} \]
The model \(\mathsf{W}\mathbf{a}\) can therefore be written as \((\mathsf{F}\mathsf{B}^{-1})\mathbf{a} = \mathsf{F}(\mathsf{B}^{-1}\mathbf{a})\,.\)
The original model \(\mathsf{F}\mathbf{c}\) is therefore identical with this if
\[ \mathbf{c} = \left(\mathsf{B}^{-1}\mathbf{a}\right) = \left[\mathbf{a}^T\left(\mathsf{B}^{-1}\right)^T\right]^T\,. \]
The reason we use \(\left(\mathsf{B}^{-1}\right)^T\) rather then \(\mathsf{B}^{-1}\) is to save storage, since \(\left(\mathsf{B}^{-1}\right)^T\) can be stored in the same matrix as \(\mathsf{B}\) (TMultiDimFit::MakeCoefficients). The errors in the coefficients is calculated by inverting the curvature matrix of the non-orthogonal functions \( f_{lj}\) [1] (TMultiDimFit::MakeCoefficientErrors).
It's important to realize that the training sample should be representative of the problem at hand, in particular along the borders of the region of interest. This is because the algorithm presented here, is a interpolation, rather then a extrapolation 5.
Also, the independent variables \( x_{i}\) need to be linear independent, since the procedure will perform poorly if they are not 5. One can find an linear transformation from ones original variables \( \xi_{i}\) to a set of linear independent variables \( x_{i}\), using a Principal Components Analysis (see TPrincipal), and then use the transformed variable as input to this class 5.
H. Wind also outlines a method for parameterising a multidimensional dependence over a multidimensional set of variables. An example of the method from 5, is a follows (please refer to 5 for a full discussion):
To process data, using this parameterisation, do
The class also provides functionality for testing the, over the training sample, found parameterization (TMultiDimFit::Fit). This is done by passing the class a test sample of \( M_t\) tuples of the form \((\mathbf{x}_{t,j},D_{t,j}, E_{t,j})\), where \(\mathbf{x}_{t,j}\) are the independent variables, \( D_{t,j}\) the known, dependent quantity, and \( E_{t,j}\) is the square error in \( D_{t,j}\) (TMultiDimFit::AddTestRow).
The parameterization is then evaluated at every \(\mathbf{x}_t\) in the test sample, and
\[ S_t \equiv \sum_{j=1}^{M_t} \left(D_{t,j} - D_p\left(\mathbf{x}_{t,j}\right)\right)^2 \]
is evaluated. The relative error over the test sample
\[ R_t = \frac{S_t}{\sum_{j=1}^{M_t} D_{t,j}^2} \]
should not be to low or high compared to \( R\) from the training sample. Also, multiple correlation coefficient from both samples should be fairly close, otherwise one of the samples is not representative of the problem. A large difference in the reduced \( \chi^2\) over the two samples indicate an over fit, and the maximum number of terms in the parameterisation should be reduced.
It's possible to use 4 to further improve the fit, using the test sample.
Christian Holm
Definition at line 25 of file TMultiDimFit.h.
Public Types | |
| enum | EMDFPolyType { kMonomials, kChebyshev, kLegendre } |
 Public Types inherited from TObject Public Types inherited from TObject | |
| enum | { kIsOnHeap = 0x01000000, kNotDeleted = 0x02000000, kZombie = 0x04000000, kBitMask = 0x00ffffff } |
| enum | { kSingleKey = BIT(0), kOverwrite = BIT(1), kWriteDelete = BIT(2) } |
| enum | EStatusBits { kCanDelete = BIT(0), kMustCleanup = BIT(3), kObjInCanvas = BIT(3), kIsReferenced = BIT(4), kHasUUID = BIT(5), kCannotPick = BIT(6), kNoContextMenu = BIT(8), kInvalidObject = BIT(13) } |
Public Member Functions | |
| TMultiDimFit () | |
| Empty CTOR. Do not use. More... | |
| TMultiDimFit (Int_t dimension, EMDFPolyType type=kMonomials, Option_t *option="") | |
| Constructor Second argument is the type of polynomials to use in parameterisation, one of: TMultiDimFit::kMonomials TMultiDimFit::kChebyshev TMultiDimFit::kLegendre. More... | |
| virtual | ~TMultiDimFit () |
| Destructor. More... | |
| virtual void | AddRow (const Double_t *x, Double_t D, Double_t E=0) |
| Add a row consisting of fNVariables independent variables, the known, dependent quantity, and optionally, the square error in the dependent quantity, to the training sample to be used for the parameterization. More... | |
| virtual void | AddTestRow (const Double_t *x, Double_t D, Double_t E=0) |
| Add a row consisting of fNVariables independent variables, the known, dependent quantity, and optionally, the square error in the dependent quantity, to the test sample to be used for the test of the parameterization. More... | |
| virtual void | Browse (TBrowser *b) |
| Browse the TMultiDimFit object in the TBrowser. More... | |
| virtual void | Clear (Option_t *option="") |
| Clear internal structures and variables. More... | |
| virtual void | Draw (Option_t *="d") |
| Default Draw method for all objects. More... | |
| virtual Double_t | Eval (const Double_t *x, const Double_t *coeff=0) const |
| Evaluate parameterization at point x. More... | |
| virtual Double_t | EvalError (const Double_t *x, const Double_t *coeff=0) const |
| Evaluate parameterization error at point x. More... | |
| virtual void | FindParameterization (Option_t *option="") |
| Find the parameterization. More... | |
| virtual void | Fit (Option_t *option="") |
| Try to fit the found parameterisation to the test sample. More... | |
| Double_t | GetChi2 () const |
| const TVectorD * | GetCoefficients () const |
| const TVectorD * | GetCoefficientsRMS () const |
| const TMatrixD * | GetCorrelationMatrix () const |
| Double_t | GetError () const |
| Int_t * | GetFunctionCodes () const |
| const TMatrixD * | GetFunctions () const |
| virtual TList * | GetHistograms () const |
| Double_t | GetMaxAngle () const |
| Int_t | GetMaxFunctions () const |
| Int_t * | GetMaxPowers () const |
| Double_t | GetMaxQuantity () const |
| Int_t | GetMaxStudy () const |
| Int_t | GetMaxTerms () const |
| const TVectorD * | GetMaxVariables () const |
| Double_t | GetMeanQuantity () const |
| const TVectorD * | GetMeanVariables () const |
| Double_t | GetMinAngle () const |
| Double_t | GetMinQuantity () const |
| Double_t | GetMinRelativeError () const |
| const TVectorD * | GetMinVariables () const |
| Int_t | GetNCoefficients () const |
| Int_t | GetNVariables () const |
| Int_t | GetPolyType () const |
| Int_t * | GetPowerIndex () const |
| Double_t | GetPowerLimit () const |
| const Int_t * | GetPowers () const |
| Double_t | GetPrecision () const |
| const TVectorD * | GetQuantity () const |
| Double_t | GetResidualMax () const |
| Int_t | GetResidualMaxRow () const |
| Double_t | GetResidualMin () const |
| Int_t | GetResidualMinRow () const |
| Double_t | GetResidualSumSq () const |
| Double_t | GetRMS () const |
| Int_t | GetSampleSize () const |
| const TVectorD * | GetSqError () const |
| Double_t | GetSumSqAvgQuantity () const |
| Double_t | GetSumSqQuantity () const |
| Double_t | GetTestError () const |
| Double_t | GetTestPrecision () const |
| const TVectorD * | GetTestQuantity () const |
| Int_t | GetTestSampleSize () const |
| const TVectorD * | GetTestSqError () const |
| const TVectorD * | GetTestVariables () const |
| const TVectorD * | GetVariables () const |
| virtual Bool_t | IsFolder () const |
| Returns kTRUE in case object contains browsable objects (like containers or lists of other objects). More... | |
| virtual Double_t | MakeChi2 (const Double_t *coeff=0) |
| Calculate Chi square over either the test sample. More... | |
| virtual void | MakeCode (const char *functionName="MDF", Option_t *option="") |
| Generate the file <filename> with .C appended if argument doesn't end in .cxx or .C. More... | |
| virtual void | MakeHistograms (Option_t *option="A") |
| Make histograms of the result of the analysis. More... | |
| virtual void | MakeMethod (const Char_t *className="MDF", Option_t *option="") |
| Generate the file <classname>MDF.cxx which contains the implementation of the method: More... | |
| virtual void | Print (Option_t *option="ps") const |
| Print statistics etc. More... | |
| void | SetBinVarX (Int_t nbbinvarx) |
| void | SetBinVarY (Int_t nbbinvary) |
| void | SetMaxAngle (Double_t angle=0) |
| Set the max angle (in degrees) between the initial data vector to be fitted, and the new candidate function to be included in the fit. More... | |
| void | SetMaxFunctions (Int_t n) |
| void | SetMaxPowers (const Int_t *powers) |
| Set the maximum power to be considered in the fit for each variable. More... | |
| void | SetMaxStudy (Int_t n) |
| void | SetMaxTerms (Int_t terms) |
| void | SetMinAngle (Double_t angle=1) |
| Set the min angle (in degrees) between a new candidate function and the subspace spanned by the previously accepted functions. More... | |
| void | SetMinRelativeError (Double_t error) |
| Set the acceptable relative error for when sum of square residuals is considered minimized. More... | |
| void | SetPowerLimit (Double_t limit=1e-3) |
| Set the user parameter for the function selection. More... | |
| virtual void | SetPowers (const Int_t *powers, Int_t terms) |
| Define a user function. More... | |
 Public Member Functions inherited from TNamed Public Member Functions inherited from TNamed | |
| TNamed () | |
| TNamed (const char *name, const char *title) | |
| TNamed (const TString &name, const TString &title) | |
| TNamed (const TNamed &named) | |
| TNamed copy ctor. More... | |
| virtual | ~TNamed () |
| virtual TObject * | Clone (const char *newname="") const |
| Make a clone of an object using the Streamer facility. More... | |
| virtual Int_t | Compare (const TObject *obj) const |
| Compare two TNamed objects. More... | |
| virtual void | Copy (TObject &named) const |
| Copy this to obj. More... | |
| virtual void | FillBuffer (char *&buffer) |
| Encode TNamed into output buffer. More... | |
| virtual const char * | GetName () const |
| Returns name of object. More... | |
| virtual const char * | GetTitle () const |
| Returns title of object. More... | |
| virtual ULong_t | Hash () const |
| Return hash value for this object. More... | |
| virtual Bool_t | IsSortable () const |
| virtual void | ls (Option_t *option="") const |
| List TNamed name and title. More... | |
| TNamed & | operator= (const TNamed &rhs) |
| TNamed assignment operator. More... | |
| virtual void | SetName (const char *name) |
| Set the name of the TNamed. More... | |
| virtual void | SetNameTitle (const char *name, const char *title) |
| Set all the TNamed parameters (name and title). More... | |
| virtual void | SetTitle (const char *title="") |
| Set the title of the TNamed. More... | |
| virtual Int_t | Sizeof () const |
| Return size of the TNamed part of the TObject. More... | |
 Public Member Functions inherited from TObject Public Member Functions inherited from TObject | |
| TObject () | |
| TObject constructor. More... | |
| TObject (const TObject &object) | |
| TObject copy ctor. More... | |
| virtual | ~TObject () |
| TObject destructor. More... | |
| void | AbstractMethod (const char *method) const |
| Use this method to implement an "abstract" method that you don't want to leave purely abstract. More... | |
| virtual void | AppendPad (Option_t *option="") |
| Append graphics object to current pad. More... | |
| virtual const char * | ClassName () const |
| Returns name of class to which the object belongs. More... | |
| virtual void | Delete (Option_t *option="") |
| Delete this object. More... | |
| virtual Int_t | DistancetoPrimitive (Int_t px, Int_t py) |
| Computes distance from point (px,py) to the object. More... | |
| virtual void | DrawClass () const |
| Draw class inheritance tree of the class to which this object belongs. More... | |
| virtual TObject * | DrawClone (Option_t *option="") const |
| Draw a clone of this object in the current pad. More... | |
| virtual void | Dump () const |
| Dump contents of object on stdout. More... | |
| virtual void | Error (const char *method, const char *msgfmt,...) const |
| Issue error message. More... | |
| virtual void | Execute (const char *method, const char *params, Int_t *error=0) |
| Execute method on this object with the given parameter string, e.g. More... | |
| virtual void | Execute (TMethod *method, TObjArray *params, Int_t *error=0) |
| Execute method on this object with parameters stored in the TObjArray. More... | |
| virtual void | ExecuteEvent (Int_t event, Int_t px, Int_t py) |
| Execute action corresponding to an event at (px,py). More... | |
| virtual void | Fatal (const char *method, const char *msgfmt,...) const |
| Issue fatal error message. More... | |
| virtual TObject * | FindObject (const char *name) const |
| Must be redefined in derived classes. More... | |
| virtual TObject * | FindObject (const TObject *obj) const |
| Must be redefined in derived classes. More... | |
| virtual Option_t * | GetDrawOption () const |
| Get option used by the graphics system to draw this object. More... | |
| virtual const char * | GetIconName () const |
| Returns mime type name of object. More... | |
| virtual char * | GetObjectInfo (Int_t px, Int_t py) const |
| Returns string containing info about the object at position (px,py). More... | |
| virtual Option_t * | GetOption () const |
| virtual UInt_t | GetUniqueID () const |
| Return the unique object id. More... | |
| virtual Bool_t | HandleTimer (TTimer *timer) |
| Execute action in response of a timer timing out. More... | |
| virtual void | Info (const char *method, const char *msgfmt,...) const |
| Issue info message. More... | |
| virtual Bool_t | InheritsFrom (const char *classname) const |
| Returns kTRUE if object inherits from class "classname". More... | |
| virtual Bool_t | InheritsFrom (const TClass *cl) const |
| Returns kTRUE if object inherits from TClass cl. More... | |
| virtual void | Inspect () const |
| Dump contents of this object in a graphics canvas. More... | |
| void | InvertBit (UInt_t f) |
| virtual Bool_t | IsEqual (const TObject *obj) const |
| Default equal comparison (objects are equal if they have the same address in memory). More... | |
| Bool_t | IsOnHeap () const |
| Bool_t | IsZombie () const |
| void | MayNotUse (const char *method) const |
| Use this method to signal that a method (defined in a base class) may not be called in a derived class (in principle against good design since a child class should not provide less functionality than its parent, however, sometimes it is necessary). More... | |
| virtual Bool_t | Notify () |
| This method must be overridden to handle object notification. More... | |
| void | Obsolete (const char *method, const char *asOfVers, const char *removedFromVers) const |
| Use this method to declare a method obsolete. More... | |
| void | operator delete (void *ptr) |
| Operator delete. More... | |
| void | operator delete[] (void *ptr) |
| Operator delete []. More... | |
| void * | operator new (size_t sz) |
| void * | operator new (size_t sz, void *vp) |
| void * | operator new[] (size_t sz) |
| void * | operator new[] (size_t sz, void *vp) |
| TObject & | operator= (const TObject &rhs) |
| TObject assignment operator. More... | |
| virtual void | Paint (Option_t *option="") |
| This method must be overridden if a class wants to paint itself. More... | |
| virtual void | Pop () |
| Pop on object drawn in a pad to the top of the display list. More... | |
| virtual Int_t | Read (const char *name) |
| Read contents of object with specified name from the current directory. More... | |
| virtual void | RecursiveRemove (TObject *obj) |
| Recursively remove this object from a list. More... | |
| void | ResetBit (UInt_t f) |
| virtual void | SaveAs (const char *filename="", Option_t *option="") const |
| Save this object in the file specified by filename. More... | |
| virtual void | SavePrimitive (std::ostream &out, Option_t *option="") |
| Save a primitive as a C++ statement(s) on output stream "out". More... | |
| void | SetBit (UInt_t f, Bool_t set) |
| Set or unset the user status bits as specified in f. More... | |
| void | SetBit (UInt_t f) |
| virtual void | SetDrawOption (Option_t *option="") |
| Set drawing option for object. More... | |
| virtual void | SetUniqueID (UInt_t uid) |
| Set the unique object id. More... | |
| virtual void | SysError (const char *method, const char *msgfmt,...) const |
| Issue system error message. More... | |
| Bool_t | TestBit (UInt_t f) const |
| Int_t | TestBits (UInt_t f) const |
| virtual void | UseCurrentStyle () |
| Set current style settings in this object This function is called when either TCanvas::UseCurrentStyle or TROOT::ForceStyle have been invoked. More... | |
| virtual void | Warning (const char *method, const char *msgfmt,...) const |
| Issue warning message. More... | |
| virtual Int_t | Write (const char *name=0, Int_t option=0, Int_t bufsize=0) |
| Write this object to the current directory. More... | |
| virtual Int_t | Write (const char *name=0, Int_t option=0, Int_t bufsize=0) const |
| Write this object to the current directory. More... | |
Static Public Member Functions | |
| static TMultiDimFit * | Instance () |
| Return the static instance. More... | |
 Static Public Member Functions inherited from TObject Static Public Member Functions inherited from TObject | |
| static Long_t | GetDtorOnly () |
| Return destructor only flag. More... | |
| static Bool_t | GetObjectStat () |
| Get status of object stat flag. More... | |
| static void | SetDtorOnly (void *obj) |
| Set destructor only flag. More... | |
| static void | SetObjectStat (Bool_t stat) |
| Turn on/off tracking of objects in the TObjectTable. More... | |
Protected Member Functions | |
| virtual Double_t | EvalControl (const Int_t *powers) const |
| PRIVATE METHOD: Calculate the control parameter from the passed powers. More... | |
| virtual Double_t | EvalFactor (Int_t p, Double_t x) const |
| PRIVATE METHOD: Evaluate function with power p at variable value x. More... | |
| virtual void | MakeCandidates () |
| PRIVATE METHOD: Create list of candidate functions for the parameterisation. More... | |
| virtual void | MakeCoefficientErrors () |
| PRIVATE METHOD: Compute the errors on the coefficients. More... | |
| virtual void | MakeCoefficients () |
| PRIVATE METHOD: Invert the model matrix B, and compute final coefficients. More... | |
| virtual void | MakeCorrelation () |
| PRIVATE METHOD: Compute the correlation matrix. More... | |
| virtual Double_t | MakeGramSchmidt (Int_t function) |
| PRIVATE METHOD: Make Gram-Schmidt orthogonalisation. More... | |
| virtual void | MakeNormalized () |
| PRIVATE METHOD: Normalize data to the interval [-1;1]. More... | |
| virtual void | MakeParameterization () |
| PRIVATE METHOD: Find the parameterization over the training sample. More... | |
| virtual void | MakeRealCode (const char *filename, const char *classname, Option_t *option="") |
| PRIVATE METHOD: This is the method that actually generates the code for the evaluation the parameterization on some point. More... | |
| virtual Bool_t | Select (const Int_t *iv) |
| Selection method. More... | |
| virtual Bool_t | TestFunction (Double_t squareResidual, Double_t dResidur) |
| PRIVATE METHOD: Test whether the currently considered function contributes to the fit. More... | |
 Protected Member Functions inherited from TObject Protected Member Functions inherited from TObject | |
| virtual void | DoError (int level, const char *location, const char *fmt, va_list va) const |
| Interface to ErrorHandler (protected). More... | |
| void | MakeZombie () |
Static Private Attributes | |
| static TMultiDimFit * | fgInstance = 0 |
#include <TMultiDimFit.h>
| Enumerator | |
|---|---|
| kMonomials | |
| kChebyshev | |
| kLegendre | |
Definition at line 28 of file TMultiDimFit.h.
| TMultiDimFit::TMultiDimFit | ( | ) |
Empty CTOR. Do not use.
Definition at line 430 of file TMultiDimFit.cxx.
| TMultiDimFit::TMultiDimFit | ( | Int_t | dimension, |
| EMDFPolyType | type = kMonomials, |
||
| Option_t * | option = "" |
||
| ) |
Constructor Second argument is the type of polynomials to use in parameterisation, one of: TMultiDimFit::kMonomials TMultiDimFit::kChebyshev TMultiDimFit::kLegendre.
Options: K Compute (k)correlation matrix V Be verbose
Default is no options.
Definition at line 505 of file TMultiDimFit.cxx.
|
virtual |
Destructor.
Definition at line 583 of file TMultiDimFit.cxx.
Add a row consisting of fNVariables independent variables, the known, dependent quantity, and optionally, the square error in the dependent quantity, to the training sample to be used for the parameterization.
The mean of the variables and quantity is calculated on the fly, as outlined in TPrincipal::AddRow. This sample should be representative of the problem at hand. Please note, that if no error is given Poisson statistics is assumed and the square error is set to the value of dependent quantity. See also the class description
Definition at line 608 of file TMultiDimFit.cxx.
Add a row consisting of fNVariables independent variables, the known, dependent quantity, and optionally, the square error in the dependent quantity, to the test sample to be used for the test of the parameterization.
This sample needn't be representative of the problem at hand. Please note, that if no error is given Poisson statistics is assumed and the square error is set to the value of dependent quantity. See also the class description
Definition at line 687 of file TMultiDimFit.cxx.
Browse the TMultiDimFit object in the TBrowser.
Reimplemented from TObject.
Definition at line 734 of file TMultiDimFit.cxx.
Clear internal structures and variables.
Reimplemented from TNamed.
Definition at line 786 of file TMultiDimFit.cxx.
Default Draw method for all objects.
Reimplemented from TObject.
Definition at line 144 of file TMultiDimFit.h.
Evaluate parameterization at point x.
Optional argument coeff is a vector of coefficients for the parameterisation, fNCoefficients elements long.
Definition at line 873 of file TMultiDimFit.cxx.
PRIVATE METHOD: Calculate the control parameter from the passed powers.
Definition at line 934 of file TMultiDimFit.cxx.
Evaluate parameterization error at point x.
Optional argument coeff is a vector of coefficients for the parameterisation, fNCoefficients elements long.
Definition at line 901 of file TMultiDimFit.cxx.
PRIVATE METHOD: Evaluate function with power p at variable value x.
Definition at line 949 of file TMultiDimFit.cxx.
Find the parameterization.
Options: None so far
For detailed description of what this entails, please refer to the class description
Definition at line 991 of file TMultiDimFit.cxx.
Try to fit the found parameterisation to the test sample.
Options M use Minuit to improve coefficients
Also, refer to class description
Definition at line 1010 of file TMultiDimFit.cxx.
|
inline |
Definition at line 150 of file TMultiDimFit.h.
|
inline |
Definition at line 152 of file TMultiDimFit.h.
|
inline |
Definition at line 153 of file TMultiDimFit.h.
|
inline |
Definition at line 151 of file TMultiDimFit.h.
|
inline |
Definition at line 154 of file TMultiDimFit.h.
|
inline |
Definition at line 155 of file TMultiDimFit.h.
|
inline |
Definition at line 156 of file TMultiDimFit.h.
|
inlinevirtual |
Definition at line 157 of file TMultiDimFit.h.
|
inline |
Definition at line 158 of file TMultiDimFit.h.
|
inline |
Definition at line 159 of file TMultiDimFit.h.
|
inline |
Definition at line 160 of file TMultiDimFit.h.
|
inline |
Definition at line 161 of file TMultiDimFit.h.
|
inline |
Definition at line 162 of file TMultiDimFit.h.
|
inline |
Definition at line 163 of file TMultiDimFit.h.
|
inline |
Definition at line 164 of file TMultiDimFit.h.
|
inline |
Definition at line 165 of file TMultiDimFit.h.
|
inline |
Definition at line 166 of file TMultiDimFit.h.
|
inline |
Definition at line 167 of file TMultiDimFit.h.
|
inline |
Definition at line 168 of file TMultiDimFit.h.
|
inline |
Definition at line 169 of file TMultiDimFit.h.
|
inline |
Definition at line 170 of file TMultiDimFit.h.
|
inline |
Definition at line 172 of file TMultiDimFit.h.
|
inline |
Definition at line 171 of file TMultiDimFit.h.
|
inline |
Definition at line 173 of file TMultiDimFit.h.
|
inline |
Definition at line 174 of file TMultiDimFit.h.
|
inline |
Definition at line 175 of file TMultiDimFit.h.
|
inline |
Definition at line 176 of file TMultiDimFit.h.
|
inline |
Definition at line 177 of file TMultiDimFit.h.
|
inline |
Definition at line 178 of file TMultiDimFit.h.
|
inline |
Definition at line 179 of file TMultiDimFit.h.
|
inline |
Definition at line 181 of file TMultiDimFit.h.
|
inline |
Definition at line 180 of file TMultiDimFit.h.
|
inline |
Definition at line 182 of file TMultiDimFit.h.
|
inline |
Definition at line 183 of file TMultiDimFit.h.
|
inline |
Definition at line 184 of file TMultiDimFit.h.
|
inline |
Definition at line 185 of file TMultiDimFit.h.
|
inline |
Definition at line 186 of file TMultiDimFit.h.
|
inline |
Definition at line 187 of file TMultiDimFit.h.
|
inline |
Definition at line 188 of file TMultiDimFit.h.
|
inline |
Definition at line 189 of file TMultiDimFit.h.
|
inline |
Definition at line 190 of file TMultiDimFit.h.
|
inline |
Definition at line 191 of file TMultiDimFit.h.
|
inline |
Definition at line 192 of file TMultiDimFit.h.
|
inline |
Definition at line 193 of file TMultiDimFit.h.
|
inline |
Definition at line 194 of file TMultiDimFit.h.
|
inline |
Definition at line 195 of file TMultiDimFit.h.
|
static |
Return the static instance.
Definition at line 1091 of file TMultiDimFit.cxx.
|
inlinevirtual |
Returns kTRUE in case object contains browsable objects (like containers or lists of other objects).
Reimplemented from TObject.
Definition at line 198 of file TMultiDimFit.h.
|
protectedvirtual |
PRIVATE METHOD: Create list of candidate functions for the parameterisation.
See also class description
Definition at line 1102 of file TMultiDimFit.cxx.
Calculate Chi square over either the test sample.
The optional argument coeff is a vector of coefficients to use in the evaluation of the parameterisation. If coeff == 0, then the found coefficients is used. Used my MINUIT for fit (see TMultDimFit::Fit)
Definition at line 1237 of file TMultiDimFit.cxx.
Generate the file <filename> with .C appended if argument doesn't end in .cxx or .C.
The contains the implementation of the function:
Double_t <funcname>(Double_t *x)
which does the same as TMultiDimFit::Eval. Please refer to this method.
Further, the static variables:
Int_t gNVariables Int_t gNCoefficients Double_t gDMean Double_t gXMean[] Double_t gXMin[] Double_t gXMax[] Double_t gCoefficient[] Int_t gPower[]
are initialized. The only ROOT header file needed is Rtypes.h
See TMultiDimFit::MakeRealCode for a list of options
Definition at line 1287 of file TMultiDimFit.cxx.
|
protectedvirtual |
PRIVATE METHOD: Compute the errors on the coefficients.
For this to be done, the curvature matrix of the non-orthogonal functions, is computed.
Definition at line 1304 of file TMultiDimFit.cxx.
|
protectedvirtual |
PRIVATE METHOD: Invert the model matrix B, and compute final coefficients.
For a more thorough discussion of what this means, please refer to the class description
First we invert the lower triangle matrix fOrthCurvatureMatrix and store the inverted matrix in the upper triangle.
Definition at line 1362 of file TMultiDimFit.cxx.
|
protectedvirtual |
PRIVATE METHOD: Compute the correlation matrix.
Definition at line 1442 of file TMultiDimFit.cxx.
PRIVATE METHOD: Make Gram-Schmidt orthogonalisation.
The class description gives a thorough account of this algorithm, as well as references. Please refer to the class description
Definition at line 1501 of file TMultiDimFit.cxx.
Make histograms of the result of the analysis.
This message should be sent after having read all data points, but before finding the parameterization
Options: A All the below X Original independent variables D Original dependent variables N Normalised independent variables S Shifted dependent variables R1 Residuals versus normalised independent variables R2 Residuals versus dependent variable R3 Residuals computed on training sample R4 Residuals computed on test sample
For a description of these quantities, refer to class description
Definition at line 1594 of file TMultiDimFit.cxx.
Generate the file <classname>MDF.cxx which contains the implementation of the method:
Double_t <classname>MDF(Double_t *x)
which does the same as TMultiDimFit::Eval. Please refer to this method.
Further, the public static members:
Int_t <classname>::fgNVariables Int_t <classname>::fgNCoefficients Double_t <classname>::fgDMean Double_t <classname>::fgXMean[] //[fgNVariables] Double_t <classname>::fgXMin[] //[fgNVariables] Double_t <classname>::fgXMax[] //[fgNVariables] Double_t <classname>::fgCoefficient[] //[fgNCoeffficents] Int_t <classname>::fgPower[] //[fgNCoeffficents*fgNVariables]
are initialized, and assumed to exist. The class declaration is assumed to be in <classname>.h and assumed to be provided by the user.
See TMultiDimFit::MakeRealCode for a list of options
The minimal class definition is:
class <classname> { public: Int_t <classname>::fgNVariables; // Number of variables Int_t <classname>::fgNCoefficients; // Number of terms Double_t <classname>::fgDMean; // Mean from training sample Double_t <classname>::fgXMean[]; // Mean from training sample Double_t <classname>::fgXMin[]; // Min from training sample Double_t <classname>::fgXMax[]; // Max from training sample Double_t <classname>::fgCoefficient[]; // Coefficients Int_t <classname>::fgPower[]; // Function powers
Double_t Eval(Double_t *x); };
Whether the method <classname>::Eval should be static or not, is up to the user.
Definition at line 1739 of file TMultiDimFit.cxx.
|
protectedvirtual |
PRIVATE METHOD: Normalize data to the interval [-1;1].
This is needed for the classes method to work.
Definition at line 1751 of file TMultiDimFit.cxx.
|
protectedvirtual |
PRIVATE METHOD: Find the parameterization over the training sample.
A full account of the algorithm is given in the class description
Definition at line 1805 of file TMultiDimFit.cxx.
|
protectedvirtual |
PRIVATE METHOD: This is the method that actually generates the code for the evaluation the parameterization on some point.
It's called by TMultiDimFit::MakeCode and TMultiDimFit::MakeMethod.
The options are: NONE so far
Definition at line 1958 of file TMultiDimFit.cxx.
Print statistics etc.
Options are P Parameters S Statistics C Coefficients R Result of parameterisation F Result of fit K Correlation Matrix M Pretty print formula
Reimplemented from TNamed.
Definition at line 2151 of file TMultiDimFit.cxx.
Selection method.
User can override this method for specialized selection of acceptable functions in fit. Default is to select all. This message is sent during the build-up of the function candidates table once for each set of powers in variables. Notice, that the argument array contains the powers PLUS ONE. For example, to De select the function f = x1^2 * x2^4 * x3^5, this method should return kFALSE if given the argument { 3, 4, 6 }
Definition at line 2358 of file TMultiDimFit.cxx.
Definition at line 205 of file TMultiDimFit.h.
Definition at line 206 of file TMultiDimFit.h.
Set the max angle (in degrees) between the initial data vector to be fitted, and the new candidate function to be included in the fit.
By default it is 0, which automatically chooses another selection criteria. See also class description
Definition at line 2370 of file TMultiDimFit.cxx.
Definition at line 208 of file TMultiDimFit.h.
Set the maximum power to be considered in the fit for each variable.
See also class description
Definition at line 2436 of file TMultiDimFit.cxx.
Definition at line 210 of file TMultiDimFit.h.
Definition at line 211 of file TMultiDimFit.h.
Set the min angle (in degrees) between a new candidate function and the subspace spanned by the previously accepted functions.
See also class description
Definition at line 2386 of file TMultiDimFit.cxx.
Set the acceptable relative error for when sum of square residuals is considered minimized.
For a full account, refer to the class description
Definition at line 2451 of file TMultiDimFit.cxx.
Set the user parameter for the function selection.
The bigger the limit, the more functions are used. The meaning of this variable is defined in the class description
Definition at line 2426 of file TMultiDimFit.cxx.
Define a user function.
The input array must be of the form (p11, ..., p1N, ... ,pL1, ..., pLN) Where N is the dimension of the data sample, L is the number of terms (given in terms) and the first number, labels the term, the second the variable. More information is given in the class description
Definition at line 2406 of file TMultiDimFit.cxx.
PRIVATE METHOD: Test whether the currently considered function contributes to the fit.
See also class description
Definition at line 2463 of file TMultiDimFit.cxx.
|
protected |
Definition at line 108 of file TMultiDimFit.h.
|
protected |
Definition at line 109 of file TMultiDimFit.h.
|
protected |
Definition at line 95 of file TMultiDimFit.h.
|
protected |
Definition at line 92 of file TMultiDimFit.h.
|
protected |
Definition at line 93 of file TMultiDimFit.h.
|
protected |
Definition at line 102 of file TMultiDimFit.h.
|
protected |
Definition at line 103 of file TMultiDimFit.h.
|
protected |
Definition at line 98 of file TMultiDimFit.h.
|
protected |
Definition at line 111 of file TMultiDimFit.h.
|
protected |
Definition at line 70 of file TMultiDimFit.h.
|
protected |
Definition at line 68 of file TMultiDimFit.h.
|
staticprivate |
Definition at line 35 of file TMultiDimFit.h.
|
protected |
Definition at line 107 of file TMultiDimFit.h.
|
protected |
Definition at line 106 of file TMultiDimFit.h.
|
protected |
Definition at line 115 of file TMultiDimFit.h.
|
protected |
Definition at line 116 of file TMultiDimFit.h.
|
protected |
Definition at line 61 of file TMultiDimFit.h.
|
protected |
Definition at line 72 of file TMultiDimFit.h.
|
protected |
Definition at line 69 of file TMultiDimFit.h.
|
protected |
Definition at line 64 of file TMultiDimFit.h.
|
protected |
Definition at line 78 of file TMultiDimFit.h.
|
protected |
Definition at line 41 of file TMultiDimFit.h.
|
protected |
Definition at line 83 of file TMultiDimFit.h.
|
protected |
Definition at line 85 of file TMultiDimFit.h.
|
protected |
Definition at line 71 of file TMultiDimFit.h.
|
protected |
Definition at line 62 of file TMultiDimFit.h.
|
protected |
Definition at line 49 of file TMultiDimFit.h.
|
protected |
Definition at line 40 of file TMultiDimFit.h.
|
protected |
Definition at line 48 of file TMultiDimFit.h.
|
protected |
Definition at line 60 of file TMultiDimFit.h.
|
protected |
Definition at line 42 of file TMultiDimFit.h.
|
protected |
Definition at line 63 of file TMultiDimFit.h.
|
protected |
Definition at line 84 of file TMultiDimFit.h.
|
protected |
Definition at line 86 of file TMultiDimFit.h.
|
protected |
Definition at line 50 of file TMultiDimFit.h.
|
protected |
Definition at line 89 of file TMultiDimFit.h.
|
protected |
Definition at line 47 of file TMultiDimFit.h.
|
protected |
Definition at line 90 of file TMultiDimFit.h.
|
protected |
Definition at line 91 of file TMultiDimFit.h.
|
protected |
Definition at line 75 of file TMultiDimFit.h.
|
protected |
Definition at line 74 of file TMultiDimFit.h.
|
protected |
Definition at line 96 of file TMultiDimFit.h.
|
protected |
Fit object (MINUIT)
Definition at line 113 of file TMultiDimFit.h.
|
protected |
Definition at line 80 of file TMultiDimFit.h.
|
protected |
Definition at line 65 of file TMultiDimFit.h.
|
protected |
Definition at line 79 of file TMultiDimFit.h.
|
protected |
Definition at line 100 of file TMultiDimFit.h.
|
protected |
Definition at line 38 of file TMultiDimFit.h.
|
protected |
Definition at line 82 of file TMultiDimFit.h.
|
protected |
Definition at line 94 of file TMultiDimFit.h.
|
protected |
Definition at line 52 of file TMultiDimFit.h.
|
protected |
Definition at line 114 of file TMultiDimFit.h.
|
protected |
Definition at line 39 of file TMultiDimFit.h.
|
protected |
Definition at line 44 of file TMultiDimFit.h.
|
protected |
Definition at line 43 of file TMultiDimFit.h.
|
protected |
Definition at line 87 of file TMultiDimFit.h.
|
protected |
Definition at line 104 of file TMultiDimFit.h.
|
protected |
Definition at line 99 of file TMultiDimFit.h.
|
protected |
Definition at line 101 of file TMultiDimFit.h.
|
protected |
Definition at line 54 of file TMultiDimFit.h.
|
protected |
Definition at line 58 of file TMultiDimFit.h.
|
protected |
Definition at line 55 of file TMultiDimFit.h.
|
protected |
Definition at line 56 of file TMultiDimFit.h.
|
protected |
Definition at line 46 of file TMultiDimFit.h.