class ROOT::Math::RichardsonDerivator
User class for calculating the derivatives of a function. It can calculate first (method Derivative1), second (method Derivative2) and third (method Derivative3) of a function. It uses the Richardson extrapolation method for function derivation in a given interval. The method use 2 derivative estimates (one computed with step h and one computed with step h/2) to compute a third, more accurate estimation. It is equivalent to the <a href = http://en.wikipedia.org/wiki/Five-point_stencil>5-point method</a>, which can be obtained with a Taylor expansion. A step size should be given, depending on x and f(x). An optimal step size value minimizes the truncation error of the expansion and the rounding error in evaluating x+h and f(x+h). A too small h will yield a too large rounding error while a too large h will give a large truncation error in the derivative approximation. A good discussion can be found in discussed in <a href=http://www.nrbook.com/a/bookcpdf/c5-7.pdf>Chapter 5.7</a> of Numerical Recipes in C. By default a value of 0.001 is uses, acceptable in many cases. This class is implemented using code previosuly in TF1::Derivate{,2,3}(). Now TF1 uses this class. @ingroup Deriv
Function Members (Methods)
public:
| ~RichardsonDerivator() | |
| double | Derivative1(double x) |
| double | Derivative1(const ROOT::Math::IGenFunction& f, double x, double h) |
| double | Derivative2(double x) |
| double | Derivative2(const ROOT::Math::IGenFunction& f, double x, double h) |
| double | Derivative3(double x) |
| double | Derivative3(const ROOT::Math::IGenFunction& f, double x, double h) |
| double | Error() const |
| double | operator()(double x) |
| ROOT::Math::RichardsonDerivator& | operator=(const ROOT::Math::RichardsonDerivator& rhs) |
| ROOT::Math::RichardsonDerivator | RichardsonDerivator(double h = 0.001) |
| ROOT::Math::RichardsonDerivator | RichardsonDerivator(const ROOT::Math::RichardsonDerivator& rhs) |
| ROOT::Math::RichardsonDerivator | RichardsonDerivator(const ROOT::Math::IGenFunction& f, double h = 0.001, bool copyFunc = false) |
| void | SetFunction(const ROOT::Math::IGenFunction& f) |
| void | SetStepSize(double h) |
Data Members
protected:
| const ROOT::Math::IGenFunction* | fFunction | pointer to function |
| bool | fFunctionCopied | flag to control if function is copied in the class |
| double | fLastError | error estimate of last derivative calculation |
| double | fStepSize | step size used for derivative calculation |
Class Charts

Function documentation
RichardsonDerivator(double h = 0.001)
Default Constructor.
Give optionally the step size for derivation. By default is 0.001, which is fine for x ~ 1
Increase if x is in averga larger or decrease if x is smaller
RichardsonDerivator(const ROOT::Math::IGenFunction& f, double h = 0.001, bool copyFunc = false)
Construct from function and step size
double Error() const
Returns the estimate of the absolute Error of the last derivative calculation.
{ return fLastError; }double Derivative1(double x)
Returns the first derivative of the function at point x,
computed by Richardson's extrapolation method (use 2 derivative estimates
to compute a third, more accurate estimation)
first, derivatives with steps h and h/2 are computed by central difference formulas
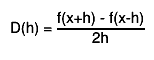 the final estimate
the final estimate 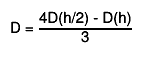 "Numerical Methods for Scientists and Engineers", H.M.Antia, 2nd edition"
the argument eps may be specified to control the step size (precision).
the step size is taken as eps*(xmax-xmin).
the default value (0.001) should be good enough for the vast majority
of functions. Give a smaller value if your function has many changes
of the second derivative in the function range.
Getting the error via TF1::DerivativeError:
(total error = roundoff error + interpolation error)
the estimate of the roundoff error is taken as follows:
"Numerical Methods for Scientists and Engineers", H.M.Antia, 2nd edition"
the argument eps may be specified to control the step size (precision).
the step size is taken as eps*(xmax-xmin).
the default value (0.001) should be good enough for the vast majority
of functions. Give a smaller value if your function has many changes
of the second derivative in the function range.
Getting the error via TF1::DerivativeError:
(total error = roundoff error + interpolation error)
the estimate of the roundoff error is taken as follows:
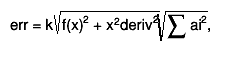 where k is the double precision, ai are coefficients used in
central difference formulas
interpolation error is decreased by making the step size h smaller.
where k is the double precision, ai are coefficients used in
central difference formulas
interpolation error is decreased by making the step size h smaller.
double Derivative1(const ROOT::Math::IGenFunction& f, double x, double h)
First Derivative calculation passing function and step-size
double Derivative2(double x)
Returns the second derivative of the function at point x,
computed by Richardson's extrapolation method (use 2 derivative estimates
to compute a third, more accurate estimation)
first, derivatives with steps h and h/2 are computed by central difference formulas
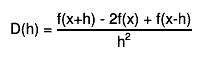 the final estimate
the final estimate 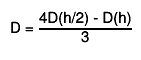 "Numerical Methods for Scientists and Engineers", H.M.Antia, 2nd edition"
the argument eps may be specified to control the step size (precision).
the step size is taken as eps*(xmax-xmin).
the default value (0.001) should be good enough for the vast majority
of functions. Give a smaller value if your function has many changes
of the second derivative in the function range.
Getting the error via TF1::DerivativeError:
(total error = roundoff error + interpolation error)
the estimate of the roundoff error is taken as follows:
"Numerical Methods for Scientists and Engineers", H.M.Antia, 2nd edition"
the argument eps may be specified to control the step size (precision).
the step size is taken as eps*(xmax-xmin).
the default value (0.001) should be good enough for the vast majority
of functions. Give a smaller value if your function has many changes
of the second derivative in the function range.
Getting the error via TF1::DerivativeError:
(total error = roundoff error + interpolation error)
the estimate of the roundoff error is taken as follows:
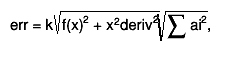 where k is the double precision, ai are coefficients used in
central difference formulas
interpolation error is decreased by making the step size h smaller.
where k is the double precision, ai are coefficients used in
central difference formulas
interpolation error is decreased by making the step size h smaller.
double Derivative2(const ROOT::Math::IGenFunction& f, double x, double h)
Second Derivative calculation passing function and step-size
double Derivative3(double x)
Returns the third derivative of the function at point x,
computed by Richardson's extrapolation method (use 2 derivative estimates
to compute a third, more accurate estimation)
first, derivatives with steps h and h/2 are computed by central difference formulas
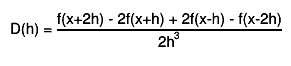 the final estimate
the final estimate 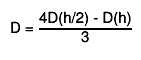 "Numerical Methods for Scientists and Engineers", H.M.Antia, 2nd edition"
the argument eps may be specified to control the step size (precision).
the step size is taken as eps*(xmax-xmin).
the default value (0.001) should be good enough for the vast majority
of functions. Give a smaller value if your function has many changes
of the second derivative in the function range.
Getting the error via TF1::DerivativeError:
(total error = roundoff error + interpolation error)
the estimate of the roundoff error is taken as follows:
"Numerical Methods for Scientists and Engineers", H.M.Antia, 2nd edition"
the argument eps may be specified to control the step size (precision).
the step size is taken as eps*(xmax-xmin).
the default value (0.001) should be good enough for the vast majority
of functions. Give a smaller value if your function has many changes
of the second derivative in the function range.
Getting the error via TF1::DerivativeError:
(total error = roundoff error + interpolation error)
the estimate of the roundoff error is taken as follows:
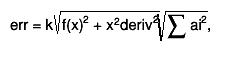 where k is the double precision, ai are coefficients used in
central difference formulas
interpolation error is decreased by making the step size h smaller.
where k is the double precision, ai are coefficients used in
central difference formulas
interpolation error is decreased by making the step size h smaller.
double Derivative3(const ROOT::Math::IGenFunction& f, double x, double h)
Third Derivative calculation passing function and step-size
void SetFunction(const ROOT::Math::IGenFunction& f)
Set function for derivative calculation (copy the function if option has been enabled in the constructor)
\@param f Function to be differentiated
void SetStepSize(double h)
Set step size for derivative calculation
\@param h step size for calculation
{ fStepSize = h; }