
class TMultiDimFit: public TNamed
/* >
Multidimensional Fits in ROOT
Overview
A common problem encountered in different fields of applied science is to find an expression for one physical quantity in terms of several others, which are directly measurable.
An example in high energy physics is the evaluation of the momentum of a charged particle from the observation of its trajectory in a magnetic field. The problem is to relate the momentum of the particle to the observations, which may consists of of positional measurements at intervals along the particle trajectory.
The exact functional relationship between the measured quantities (e.g., the space-points) and the dependent quantity (e.g., the momentum) is in general not known, but one possible way of solving the problem, is to find an expression which reliably approximates the dependence of the momentum on the observations.
This explicit function of the observations can be obtained by a least squares fitting procedure applied to a representive sample of the data, for which the dependent quantity (e.g., momentum) and the independent observations are known. The function can then be used to compute the quantity of interest for new observations of the independent variables.
This class TMultiDimFit implements such a procedure in ROOT. It is largely based on the CERNLIB MUDIFI package [2]. Though the basic concepts are still sound, and therefore kept, a few implementation details have changed, and this class can take advantage of MINUIT [4] to improve the errors of the fitting, thanks to the class TMinuit.
In [5] and [6] H. Wind demonstrates the utility of this procedure in the context of tracking, magnetic field parameterisation, and so on. The outline of the method used in this class is based on Winds discussion, and I refer these two excellents text for more information.
And example of usage is given in $ROOTSYS/tutorials/fit/multidimfit.C.
The Method
Let ![]() by the dependent quantity of interest, which depends smoothly
on the observable quantities
by the dependent quantity of interest, which depends smoothly
on the observable quantities
![]() , which we'll denote by
, which we'll denote by
![]() . Given a training sample of
. Given a training sample of ![]() tuples of the form,
(TMultiDimFit::AddRow)
tuples of the form,
(TMultiDimFit::AddRow)
such that
is minimal. Here
So what TMultiDimFit does, is to determine the number of
terms ![]() , and then
, and then ![]() terms (or functions)
terms (or functions) ![]() , and the
, and the ![]() coefficients
coefficients ![]() , so that
, so that ![]() is minimal
(TMultiDimFit::FindParameterization).
is minimal
(TMultiDimFit::FindParameterization).
Of course it's more than a little unlikely that ![]() will ever become
exact zero as a result of the procedure outlined below. Therefore, the
user is asked to provide a minimum relative error
will ever become
exact zero as a result of the procedure outlined below. Therefore, the
user is asked to provide a minimum relative error ![]() (TMultiDimFit::SetMinRelativeError), and
(TMultiDimFit::SetMinRelativeError), and ![]() will be considered minimized when
will be considered minimized when
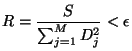
Optionally, the user may impose a functional expression by specifying
the powers of each variable in ![]() specified functions
specified functions
![]() (TMultiDimFit::SetPowers). In that case, only the
coefficients
(TMultiDimFit::SetPowers). In that case, only the
coefficients ![]() is calculated by the class.
is calculated by the class.
Limiting the Number of Terms
As always when dealing with fits, there's a real chance of
over fitting. As is well-known, it's always possible to fit an
![]() polynomial in
polynomial in ![]() to
to ![]() points
points ![]() with
with
![]() , but
the polynomial is not likely to fit new data at all
[1]. Therefore, the user is asked to provide an upper
limit,
, but
the polynomial is not likely to fit new data at all
[1]. Therefore, the user is asked to provide an upper
limit, ![]() to the number of terms in
to the number of terms in ![]() (TMultiDimFit::SetMaxTerms).
(TMultiDimFit::SetMaxTerms).
However, since there's an infinite number of ![]() to choose from, the
user is asked to give the maximum power.
to choose from, the
user is asked to give the maximum power. ![]() , of each variable
, of each variable
![]() to be considered in the minimization of
to be considered in the minimization of ![]() (TMultiDimFit::SetMaxPowers).
(TMultiDimFit::SetMaxPowers).
One way of obtaining values for the maximum power in variable ![]() , is
to perform a regular fit to the dependent quantity
, is
to perform a regular fit to the dependent quantity ![]() , using a
polynomial only in
, using a
polynomial only in ![]() . The maximum power is
. The maximum power is ![]() is then the
power that does not significantly improve the one-dimensional
least-square fit over
is then the
power that does not significantly improve the one-dimensional
least-square fit over ![]() to
to ![]() [5].
[5].
There are still a huge amount of possible choices for ![]() ; in fact
there are
; in fact
there are
![]() possible
choices. Obviously we need to limit this. To this end, the user is
asked to set a power control limit,
possible
choices. Obviously we need to limit this. To this end, the user is
asked to set a power control limit, ![]() (TMultiDimFit::SetPowerLimit), and a function
(TMultiDimFit::SetPowerLimit), and a function
![]() is only accepted if
is only accepted if
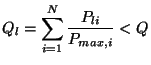
Gram-Schmidt Orthogonalisation
To further reduce the number of functions in the final expression,
only those functions that significantly reduce ![]() is chosen. What
`significant' means, is chosen by the user, and will be
discussed below (see 2.3).
is chosen. What
`significant' means, is chosen by the user, and will be
discussed below (see 2.3).
The functions ![]() are generally not orthogonal, which means one will
have to evaluate all possible
are generally not orthogonal, which means one will
have to evaluate all possible ![]() 's over all data-points before
finding the most significant [1]. We can, however, do
better then that. By applying the modified Gram-Schmidt
orthogonalisation algorithm [5] [3] to the
functions
's over all data-points before
finding the most significant [1]. We can, however, do
better then that. By applying the modified Gram-Schmidt
orthogonalisation algorithm [5] [3] to the
functions ![]() , we can evaluate the contribution to the reduction of
, we can evaluate the contribution to the reduction of
![]() from each function in turn, and we may delay the actual inversion
of the curvature-matrix
(TMultiDimFit::MakeGramSchmidt).
from each function in turn, and we may delay the actual inversion
of the curvature-matrix
(TMultiDimFit::MakeGramSchmidt).
So we are let to consider an ![]() matrix
matrix
![]() , an
element of which is given by
, an
element of which is given by
where
and
We now take as a new model
![]() . We thus want to
minimize
. We thus want to
minimize
where
or
Let
Using (9), we see that
So for each new function ![]() included in the model, we get a
reduction of the sum of squares of residuals of
included in the model, we get a
reduction of the sum of squares of residuals of
![]() ,
where
,
where
![]() is given by (4) and
is given by (4) and ![]() by
(9). Thus, using the Gram-Schmidt orthogonalisation, we
can decide if we want to include this function in the final model,
before the matrix inversion.
by
(9). Thus, using the Gram-Schmidt orthogonalisation, we
can decide if we want to include this function in the final model,
before the matrix inversion.
Function Selection Based on Residual
Supposing that ![]() steps of the procedure have been performed, the
problem now is to consider the
steps of the procedure have been performed, the
problem now is to consider the
![]() function.
function.
The sum of squares of residuals can be written as
where the relation (9) have been taken into account. The contribution of the
Two test are now applied to decide whether this
![]() function is to be included in the final expression, or not.
function is to be included in the final expression, or not.
Test 1
Denoting by ![]() the subspace spanned by
the subspace spanned by
![]() the function
the function
![]() is
by construction (see (4)) the projection of the function
is
by construction (see (4)) the projection of the function
![]() onto the direction perpendicular to
onto the direction perpendicular to ![]() . Now, if the
length of
. Now, if the
length of
![]() (given by
(given by
![]() )
is very small compared to the length of
)
is very small compared to the length of
![]() this new
function can not contribute much to the reduction of the sum of
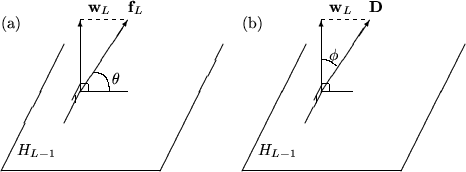
squares of residuals. The test consists then in calculating the angle
this new
function can not contribute much to the reduction of the sum of
squares of residuals. The test consists then in calculating the angle
![]() between the two vectors
between the two vectors
![]() and
and
![]() (see also figure 1) and requiring that it's
greater then a threshold value which the user must set
(TMultiDimFit::SetMinAngle).
(see also figure 1) and requiring that it's
greater then a threshold value which the user must set
(TMultiDimFit::SetMinAngle).
Test 2
Let
![]() be the data vector to be fitted. As illustrated in
figure 1, the
be the data vector to be fitted. As illustrated in
figure 1, the
![]() function
function
![]() will contribute significantly to the reduction of
will contribute significantly to the reduction of ![]() , if the angle
, if the angle
![]() between
between
![]() and
and
![]() is smaller than
an upper limit
is smaller than
an upper limit ![]() , defined by the user
(TMultiDimFit::SetMaxAngle)
, defined by the user
(TMultiDimFit::SetMaxAngle)
However, the method automatically readjusts the value of this angle
while fitting is in progress, in order to make the selection criteria
less and less difficult to be fulfilled. The result is that the
functions contributing most to the reduction of ![]() are chosen first
(TMultiDimFit::TestFunction).
are chosen first
(TMultiDimFit::TestFunction).
In case ![]() isn't defined, an alternative method of
performing this second test is used: The
isn't defined, an alternative method of
performing this second test is used: The
![]() function
function
![]() is accepted if (refer also to equation (13))
is accepted if (refer also to equation (13))
where
>From this we see, that by restricting ![]() -- the number of
terms in the final model -- the fit is more difficult to perform,
since the above selection criteria is more limiting.
-- the number of
terms in the final model -- the fit is more difficult to perform,
since the above selection criteria is more limiting.
The more coefficients we evaluate, the more the sum of squares of
residuals ![]() will be reduced. We can evaluate
will be reduced. We can evaluate ![]() before inverting
before inverting
![]() as shown below.
as shown below.
Coefficients and Coefficient Errors
Having found a parameterization, that is the ![]() 's and
's and ![]() , that
minimizes
, that
minimizes ![]() , we still need to determine the coefficients
, we still need to determine the coefficients
![]() . However, it's a feature of how we choose the significant
functions, that the evaluation of the
. However, it's a feature of how we choose the significant
functions, that the evaluation of the ![]() 's becomes trivial
[5]. To derive
's becomes trivial
[5]. To derive
![]() , we first note that
equation (4) can be written as
, we first note that
equation (4) can be written as
where
Consequently,
The model
The reason we use
Considerations
It's important to realize that the training sample should be representive of the problem at hand, in particular along the borders of the region of interest. This is because the algorithm presented here, is a interpolation, rahter then a extrapolation [5].
Also, the independent variables ![]() need to be linear
independent, since the procedure will perform poorly if they are not
[5]. One can find an linear transformation from ones
original variables
need to be linear
independent, since the procedure will perform poorly if they are not
[5]. One can find an linear transformation from ones
original variables ![]() to a set of linear independent variables
to a set of linear independent variables
![]() , using a Principal Components Analysis
(see TPrincipal), and
then use the transformed variable as input to this class [5]
[6].
, using a Principal Components Analysis
(see TPrincipal), and
then use the transformed variable as input to this class [5]
[6].
H. Wind also outlines a method for parameterising a multidimensional dependence over a multidimensional set of variables. An example of the method from [5], is a follows (please refer to [5] for a full discussion):
- Define
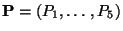 are the 5 dependent
quantities that define a track.
are the 5 dependent
quantities that define a track.
- Compute, for
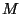 different values of
different values of
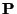 , the tracks
through the magnetic field, and determine the corresponding
, the tracks
through the magnetic field, and determine the corresponding
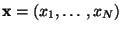 .
.
- Use the simulated observations to determine, with a simple
approximation, the values of
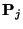 . We call these values
. We call these values
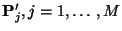 .
.
- Determine from
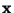 a set of at least five relevant
coordinates
a set of at least five relevant
coordinates
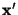 , using contrains, or
alternative:
, using contrains, or
alternative:
- Perform a Principal Component Analysis (using
TPrincipal), and use
to get a linear transformation
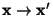 , so that
, so that
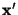 are constrained and linear independent.
are constrained and linear independent.
- Perform a Principal Component Analysis on
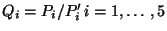 , to get linear
indenpendent (among themselves, but not independent of
, to get linear
indenpendent (among themselves, but not independent of
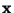 ) quantities
) quantities
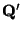
- For each component
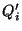 make a mutlidimensional fit,
using
make a mutlidimensional fit,
using
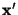 as the variables, thus determing a set of
coefficents
as the variables, thus determing a set of
coefficents
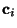 .
.
To process data, using this parameterisation, do
- Test wether the observation
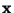 within the domain of
the parameterization, using the result from the Principal Component
Analysis.
within the domain of
the parameterization, using the result from the Principal Component
Analysis.
- Determine
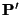 as before.
as before.
- Detetmine
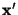 as before.
as before.
- Use the result of the fit to determind
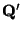 .
.
- Transform back to
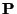 from
from
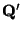 , using
the result from the Principal Component Analysis.
, using
the result from the Principal Component Analysis.
Testing the parameterization
The class also provides functionality for testing the, over the
training sample, found parameterization
(TMultiDimFit::Fit). This is done by passing
the class a test sample of ![]() tuples of the form
tuples of the form
![]() , where
, where
![]() are the independent
variables,
are the independent
variables, ![]() the known, dependent quantity, and
the known, dependent quantity, and ![]() is
the square error in
is
the square error in ![]() (TMultiDimFit::AddTestRow).
(TMultiDimFit::AddTestRow).
The parameterization is then evaluated at every
![]() in the
test sample, and
in the
test sample, and
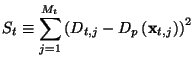
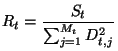
It's possible to use Minuit [4] to further improve the fit, using the test sample.
November 2000, NBI
Bibliography
- 1
-
Philip R. Bevington and D. Keith Robinson.
Data Reduction and Error Analysis for the Physical Sciences.
McGraw-Hill, 2 edition, 1992. - 2
-
René Brun et al.
Mudifi.
Long writeup DD/75-23, CERN, 1980. - 3
-
Gene H. Golub and Charles F. van Loan.
Matrix Computations.
John Hopkins Univeristy Press, Baltimore, 3 edition, 1996. - 4
-
F. James.
Minuit.
Long writeup D506, CERN, 1998. - 5
-
H. Wind.
Function parameterization.
In Proceedings of the 1972 CERN Computing and Data Processing School, volume 72-21 of Yellow report. CERN, 1972. - 6
-
H. Wind.
1. principal component analysis, 2. pattern recognition for track finding, 3. interpolation and functional representation.
Yellow report EP/81-12, CERN, 1981.
*/
Function Members (Methods)
| TMultiDimFit() | |
| TMultiDimFit(const TMultiDimFit&) | |
| TMultiDimFit(Int_t dimension, TMultiDimFit::EMDFPolyType type = kMonomials, Option_t* option = "") | |
| virtual | ~TMultiDimFit() |
| void | TObject::AbstractMethod(const char* method) const |
| virtual void | AddRow(const Double_t* x, Double_t D, Double_t E = 0) |
| virtual void | AddTestRow(const Double_t* x, Double_t D, Double_t E = 0) |
| virtual void | TObject::AppendPad(Option_t* option = "") |
| virtual void | Browse(TBrowser* b) |
| static TClass* | Class() |
| virtual const char* | TObject::ClassName() const |
| virtual void | Clear(Option_t* option = "")MENU |
| virtual TObject* | TNamed::Clone(const char* newname = "") const |
| virtual Int_t | TNamed::Compare(const TObject* obj) const |
| virtual void | TNamed::Copy(TObject& named) const |
| virtual void | TObject::Delete(Option_t* option = "")MENU |
| virtual Int_t | TObject::DistancetoPrimitive(Int_t px, Int_t py) |
| virtual void | Draw(Option_t* = "d") |
| virtual void | TObject::DrawClass() constMENU |
| virtual TObject* | TObject::DrawClone(Option_t* option = "") constMENU |
| virtual void | TObject::Dump() constMENU |
| virtual void | TObject::Error(const char* method, const char* msgfmt) const |
| virtual Double_t | Eval(const Double_t* x, const Double_t* coeff = 0) const |
| virtual Double_t | EvalError(const Double_t* x, const Double_t* coeff = 0) const |
| virtual void | TObject::Execute(const char* method, const char* params, Int_t* error = 0) |
| virtual void | TObject::Execute(TMethod* method, TObjArray* params, Int_t* error = 0) |
| virtual void | TObject::ExecuteEvent(Int_t event, Int_t px, Int_t py) |
| virtual void | TObject::Fatal(const char* method, const char* msgfmt) const |
| virtual void | TNamed::FillBuffer(char*& buffer) |
| virtual TObject* | TObject::FindObject(const char* name) const |
| virtual TObject* | TObject::FindObject(const TObject* obj) const |
| virtual void | FindParameterization(Option_t* option = "")MENU |
| virtual void | Fit(Option_t* option = "")MENU |
| Double_t | GetChi2() const |
| const TVectorD* | GetCoefficients() const |
| const TVectorD* | GetCoefficientsRMS() const |
| const TMatrixD* | GetCorrelationMatrix() const |
| virtual Option_t* | TObject::GetDrawOption() const |
| static Long_t | TObject::GetDtorOnly() |
| Double_t | GetError() const |
| Int_t* | GetFunctionCodes() const |
| const TMatrixD* | GetFunctions() const |
| virtual TList* | GetHistograms() const |
| virtual const char* | TObject::GetIconName() const |
| Double_t | GetMaxAngle() const |
| Int_t | GetMaxFunctions() const |
| Int_t* | GetMaxPowers() const |
| Double_t | GetMaxQuantity() const |
| Int_t | GetMaxStudy() const |
| Int_t | GetMaxTerms() const |
| const TVectorD* | GetMaxVariables() const |
| Double_t | GetMeanQuantity() const |
| const TVectorD* | GetMeanVariables() const |
| Double_t | GetMinAngle() const |
| Double_t | GetMinQuantity() const |
| Double_t | GetMinRelativeError() const |
| const TVectorD* | GetMinVariables() const |
| virtual const char* | TNamed::GetName() const |
| Int_t | GetNCoefficients() const |
| Int_t | GetNVariables() const |
| virtual char* | TObject::GetObjectInfo(Int_t px, Int_t py) const |
| static Bool_t | TObject::GetObjectStat() |
| virtual Option_t* | TObject::GetOption() const |
| Int_t | GetPolyType() const |
| Int_t* | GetPowerIndex() const |
| Double_t | GetPowerLimit() const |
| const Int_t* | GetPowers() const |
| Double_t | GetPrecision() const |
| const TVectorD* | GetQuantity() const |
| Double_t | GetResidualMax() const |
| Int_t | GetResidualMaxRow() const |
| Double_t | GetResidualMin() const |
| Int_t | GetResidualMinRow() const |
| Double_t | GetResidualSumSq() const |
| Double_t | GetRMS() const |
| Int_t | GetSampleSize() const |
| const TVectorD* | GetSqError() const |
| Double_t | GetSumSqAvgQuantity() const |
| Double_t | GetSumSqQuantity() const |
| Double_t | GetTestError() const |
| Double_t | GetTestPrecision() const |
| const TVectorD* | GetTestQuantity() const |
| Int_t | GetTestSampleSize() const |
| const TVectorD* | GetTestSqError() const |
| const TVectorD* | GetTestVariables() const |
| virtual const char* | TNamed::GetTitle() const |
| virtual UInt_t | TObject::GetUniqueID() const |
| const TVectorD* | GetVariables() const |
| virtual Bool_t | TObject::HandleTimer(TTimer* timer) |
| virtual ULong_t | TNamed::Hash() const |
| virtual void | TObject::Info(const char* method, const char* msgfmt) const |
| virtual Bool_t | TObject::InheritsFrom(const char* classname) const |
| virtual Bool_t | TObject::InheritsFrom(const TClass* cl) const |
| virtual void | TObject::Inspect() constMENU |
| static TMultiDimFit* | Instance() |
| void | TObject::InvertBit(UInt_t f) |
| virtual TClass* | IsA() const |
| virtual Bool_t | TObject::IsEqual(const TObject* obj) const |
| virtual Bool_t | IsFolder() const |
| Bool_t | TObject::IsOnHeap() const |
| virtual Bool_t | TNamed::IsSortable() const |
| Bool_t | TObject::IsZombie() const |
| virtual void | TNamed::ls(Option_t* option = "") const |
| virtual Double_t | MakeChi2(const Double_t* coeff = 0) |
| virtual void | MakeCode(const char* functionName = "MDF", Option_t* option = "")MENU |
| virtual void | MakeHistograms(Option_t* option = "A")MENU |
| virtual void | MakeMethod(const Char_t* className = "MDF", Option_t* option = "")MENU |
| void | TObject::MayNotUse(const char* method) const |
| virtual Bool_t | TObject::Notify() |
| void | TObject::Obsolete(const char* method, const char* asOfVers, const char* removedFromVers) const |
| static void | TObject::operator delete(void* ptr) |
| static void | TObject::operator delete(void* ptr, void* vp) |
| static void | TObject::operator delete[](void* ptr) |
| static void | TObject::operator delete[](void* ptr, void* vp) |
| void* | TObject::operator new(size_t sz) |
| void* | TObject::operator new(size_t sz, void* vp) |
| void* | TObject::operator new[](size_t sz) |
| void* | TObject::operator new[](size_t sz, void* vp) |
| TMultiDimFit& | operator=(const TMultiDimFit&) |
| virtual void | TObject::Paint(Option_t* option = "") |
| virtual void | TObject::Pop() |
| virtual void | Print(Option_t* option = "ps") constMENU |
| virtual Int_t | TObject::Read(const char* name) |
| virtual void | TObject::RecursiveRemove(TObject* obj) |
| void | TObject::ResetBit(UInt_t f) |
| virtual void | TObject::SaveAs(const char* filename = "", Option_t* option = "") constMENU |
| virtual void | TObject::SavePrimitive(ostream& out, Option_t* option = "") |
| void | SetBinVarX(Int_t nbbinvarx) |
| void | SetBinVarY(Int_t nbbinvary) |
| void | TObject::SetBit(UInt_t f) |
| void | TObject::SetBit(UInt_t f, Bool_t set) |
| virtual void | TObject::SetDrawOption(Option_t* option = "")MENU |
| static void | TObject::SetDtorOnly(void* obj) |
| void | SetMaxAngle(Double_t angle = 0) |
| void | SetMaxFunctions(Int_t n) |
| void | SetMaxPowers(const Int_t* powers) |
| void | SetMaxStudy(Int_t n) |
| void | SetMaxTerms(Int_t terms) |
| void | SetMinAngle(Double_t angle = 1) |
| void | SetMinRelativeError(Double_t error) |
| virtual void | TNamed::SetName(const char* name)MENU |
| virtual void | TNamed::SetNameTitle(const char* name, const char* title) |
| static void | TObject::SetObjectStat(Bool_t stat) |
| void | SetPowerLimit(Double_t limit = 1e-3) |
| virtual void | SetPowers(const Int_t* powers, Int_t terms) |
| virtual void | TNamed::SetTitle(const char* title = "")MENU |
| virtual void | TObject::SetUniqueID(UInt_t uid) |
| virtual void | ShowMembers(TMemberInspector&) |
| virtual Int_t | TNamed::Sizeof() const |
| virtual void | Streamer(TBuffer&) |
| void | StreamerNVirtual(TBuffer& ClassDef_StreamerNVirtual_b) |
| virtual void | TObject::SysError(const char* method, const char* msgfmt) const |
| Bool_t | TObject::TestBit(UInt_t f) const |
| Int_t | TObject::TestBits(UInt_t f) const |
| virtual void | TObject::UseCurrentStyle() |
| virtual void | TObject::Warning(const char* method, const char* msgfmt) const |
| virtual Int_t | TObject::Write(const char* name = 0, Int_t option = 0, Int_t bufsize = 0) |
| virtual Int_t | TObject::Write(const char* name = 0, Int_t option = 0, Int_t bufsize = 0) const |
| virtual void | TObject::DoError(int level, const char* location, const char* fmt, va_list va) const |
| virtual Double_t | EvalControl(const Int_t* powers) const |
| virtual Double_t | EvalFactor(Int_t p, Double_t x) const |
| virtual void | MakeCandidates() |
| virtual void | MakeCoefficientErrors() |
| virtual void | MakeCoefficients() |
| virtual void | MakeCorrelation() |
| virtual Double_t | MakeGramSchmidt(Int_t function) |
| virtual void | MakeNormalized() |
| virtual void | MakeParameterization() |
| virtual void | MakeRealCode(const char* filename, const char* classname, Option_t* option = "") |
| void | TObject::MakeZombie() |
| virtual Bool_t | Select(const Int_t* iv) |
| virtual Bool_t | TestFunction(Double_t squareResidual, Double_t dResidur) |
Data Members
| enum EMDFPolyType { | kMonomials | |
| kChebyshev | ||
| kLegendre | ||
| }; | ||
| enum TObject::EStatusBits { | kCanDelete | |
| kMustCleanup | ||
| kObjInCanvas | ||
| kIsReferenced | ||
| kHasUUID | ||
| kCannotPick | ||
| kNoContextMenu | ||
| kInvalidObject | ||
| }; | ||
| enum TObject::[unnamed] { | kIsOnHeap | |
| kNotDeleted | ||
| kZombie | ||
| kBitMask | ||
| kSingleKey | ||
| kOverwrite | ||
| kWriteDelete | ||
| }; |
| Int_t | fBinVarX | Number of bin in independent variables |
| Int_t | fBinVarY | Number of bin in dependent variables |
| Double_t | fChi2 | Chi square of fit |
| TVectorD | fCoefficients | Vector of the final coefficients |
| TVectorD | fCoefficientsRMS | Vector of RMS of coefficients |
| Double_t | fCorrelationCoeff | Multi Correlation coefficient |
| TMatrixD | fCorrelationMatrix | Correlation matrix |
| Double_t | fError | Error from parameterization |
| TVirtualFitter* | fFitter | ! Fit object (MINUIT) |
| Int_t* | fFunctionCodes | [fMaxFunctions] acceptance code |
| TMatrixD | fFunctions | Functions evaluated over sample |
| Byte_t | fHistogramMask | Bit pattern of hisograms used |
| TList* | fHistograms | List of histograms |
| Bool_t | fIsUserFunction | Flag for user defined function |
| Bool_t | fIsVerbose | |
| Double_t | fMaxAngle | Max angle for acepting new function |
| Int_t | fMaxFuncNV | fMaxFunctions*fNVariables |
| Int_t | fMaxFunctions | max number of functions |
| Int_t* | fMaxPowers | [fNVariables] maximum powers |
| Int_t* | fMaxPowersFinal | [fNVariables] maximum powers from fit; |
| Double_t | fMaxQuantity | Max value of dependent quantity |
| Double_t | fMaxResidual | Max redsidual value |
| Int_t | fMaxResidualRow | Row giving max residual |
| Int_t | fMaxStudy | max functions to study |
| Int_t | fMaxTerms | Max terms expected in final expr. |
| TVectorD | fMaxVariables | max value of independent variables |
| Double_t | fMeanQuantity | Mean of dependent quantity |
| TVectorD | fMeanVariables | mean value of independent variables |
| Double_t | fMinAngle | Min angle for acepting new function |
| Double_t | fMinQuantity | Min value of dependent quantity |
| Double_t | fMinRelativeError | Min relative error accepted |
| Double_t | fMinResidual | Min redsidual value |
| Int_t | fMinResidualRow | Row giving min residual |
| TVectorD | fMinVariables | min value of independent variables |
| Int_t | fNCoefficients | Dimension of model coefficients |
| Int_t | fNVariables | Number of independent variables |
| TString | TNamed::fName | object identifier |
| TVectorD | fOrthCoefficients | The model coefficients |
| TMatrixD | fOrthCurvatureMatrix | Model matrix |
| TVectorD | fOrthFunctionNorms | Norm of the evaluated functions |
| TMatrixD | fOrthFunctions | As above, but orthogonalised |
| Int_t | fParameterisationCode | Exit code of parameterisation |
| TMultiDimFit::EMDFPolyType | fPolyType | Type of polynomials to use |
| Int_t* | fPowerIndex | [fMaxTerms] Index of accepted powers |
| Double_t | fPowerLimit | Control parameter |
| Int_t* | fPowers | [fMaxFuncNV] where fMaxFuncNV = fMaxFunctions*fNVariables |
| Double_t | fPrecision | Relative precision of param |
| TVectorD | fQuantity | Training sample, dependent quantity |
| Double_t | fRMS | Root mean square of fit |
| TVectorD | fResiduals | Vector of the final residuals |
| Int_t | fSampleSize | Size of training sample |
| Bool_t | fShowCorrelation | print correlation matrix |
| TVectorD | fSqError | Training sample, error in quantity |
| Double_t | fSumSqAvgQuantity | Sum of squares away from mean |
| Double_t | fSumSqQuantity | SumSquare of dependent quantity |
| Double_t | fSumSqResidual | Sum of Square residuals |
| Double_t | fTestCorrelationCoeff | Multi Correlation coefficient |
| Double_t | fTestError | Error from test |
| Double_t | fTestPrecision | Relative precision of test |
| TVectorD | fTestQuantity | Test sample, dependent quantity |
| Int_t | fTestSampleSize | Size of test sample |
| TVectorD | fTestSqError | Test sample, Error in quantity |
| TVectorD | fTestVariables | Test sample, independent variables |
| TString | TNamed::fTitle | object title |
| TVectorD | fVariables | Training sample, independent variables |
| static TMultiDimFit* | fgInstance | Static instance |
Class Charts

Function documentation
Constructor
Second argument is the type of polynomials to use in
parameterisation, one of:
TMultiDimFit::kMonomials
TMultiDimFit::kChebyshev
TMultiDimFit::kLegendre
Options:
K Compute (k)correlation matrix
V Be verbose
Default is no options.
Add a row consisting of fNVariables independent variables, the known, dependent quantity, and optionally, the square error in the dependent quantity, to the training sample to be used for the parameterization. The mean of the variables and quantity is calculated on the fly, as outlined in TPrincipal::AddRow. This sample should be representive of the problem at hand. Please note, that if no error is given Poisson statistics is assumed and the square error is set to the value of dependent quantity. See also theclass description
Add a row consisting of fNVariables independent variables, the known, dependent quantity, and optionally, the square error in the dependent quantity, to the test sample to be used for the test of the parameterization. This sample needn't be representive of the problem at hand. Please note, that if no error is given Poisson statistics is assumed and the square error is set to the value of dependent quantity. See also theclass description
Evaluate parameterization at point x. Optional argument coeff is a vector of coefficients for the parameterisation, fNCoefficients elements long.
Evaluate parameterization error at point x. Optional argument coeff is a vector of coefficients for the parameterisation, fNCoefficients elements long.
PRIVATE METHOD: Calculate the control parameter from the passed powers
PRIVATE METHOD: Evaluate function with power p at variable value x
Find the parameterization
Options:
None so far
For detailed description of what this entails, please refer to the
class description
Try to fit the found parameterisation to the test sample.
Options
M use Minuit to improve coefficients
Also, refer to
class description
PRIVATE METHOD: Create list of candidate functions for the parameterisation. See alsoclass description
Calculate Chi square over either the test sample. The optional argument coeff is a vector of coefficients to use in the evaluation of the parameterisation. If coeff == 0, then the found coefficients is used. Used my MINUIT for fit (see TMultDimFit::Fit)
Generate the file <filename> with .C appended if argument doesn't end in .cxx or .C. The contains the implementation of the function: Double_t <funcname>(Double_t *x) which does the same as TMultiDimFit::Eval. Please refer to this method. Further, the static variables: Int_t gNVariables Int_t gNCoefficients Double_t gDMean Double_t gXMean[] Double_t gXMin[] Double_t gXMax[] Double_t gCoefficient[] Int_t gPower[] are initialized. The only ROOT header file needed is Rtypes.h See TMultiDimFit::MakeRealCode for a list of options
PRIVATE METHOD: Compute the errors on the coefficients. For this to be done, the curvature matrix of the non-orthogonal functions, is computed.
PRIVATE METHOD: Invert the model matrix B, and compute final coefficients. For a more thorough discussion of what this means, please refer to theclass description
First we invert the lower triangle matrix fOrthCurvatureMatrix and store the inverted matrix in the upper triangle.
PRIVATE METHOD: Make Gram-Schmidt orthogonalisation. The class description gives a thorough account of this algorithm, as well as references. Please refer to theclass description
Make histograms of the result of the analysis. This message
should be sent after having read all data points, but before
finding the parameterization
Options:
A All the below
X Original independent variables
D Original dependent variables
N Normalised independent variables
S Shifted dependent variables
R1 Residuals versus normalised independent variables
R2 Residuals versus dependent variable
R3 Residuals computed on training sample
R4 Residuals computed on test sample
For a description of these quantities, refer to
class description
Generate the file <classname>MDF.cxx which contains the implementation of the method: Double_t <classname>::MDF(Double_t *x) which does the same as TMultiDimFit::Eval. Please refer to this method. Further, the public static members: Int_t <classname>::fgNVariables Int_t <classname>::fgNCoefficients Double_t <classname>::fgDMean Double_t <classname>::fgXMean[] //[fgNVariables] Double_t <classname>::fgXMin[] //[fgNVariables] Double_t <classname>::fgXMax[] //[fgNVariables] Double_t <classname>::fgCoefficient[] //[fgNCoeffficents] Int_t <classname>::fgPower[] //[fgNCoeffficents*fgNVariables] are initialized, and assumed to exist. The class declaration is assumed to be in <classname>.h and assumed to be provided by the user. See TMultiDimFit::MakeRealCode for a list of options The minimal class definition is: class <classname> { public: Int_t <classname>::fgNVariables; // Number of variables Int_t <classname>::fgNCoefficients; // Number of terms Double_t <classname>::fgDMean; // Mean from training sample Double_t <classname>::fgXMean[]; // Mean from training sample Double_t <classname>::fgXMin[]; // Min from training sample Double_t <classname>::fgXMax[]; // Max from training sample Double_t <classname>::fgCoefficient[]; // Coefficients Int_t <classname>::fgPower[]; // Function powers Double_t Eval(Double_t *x); }; Whether the method <classname>::Eval should be static or not, is up to the user.
PRIVATE METHOD: Normalize data to the interval [-1;1]. This is needed for the classes method to work.
PRIVATE METHOD: Find the parameterization over the training sample. A full account of the algorithm is given in theclass description
PRIVATE METHOD: This is the method that actually generates the code for the evaluation the parameterization on some point. It's called by TMultiDimFit::MakeCode and TMultiDimFit::MakeMethod. The options are: NONE so far
Print statistics etc. Options are P Parameters S Statistics C Coefficients R Result of parameterisation F Result of fit K Correlation Matrix M Pretty print formula
Selection method. User can override this method for specialized
selection of acceptable functions in fit. Default is to select
all. This message is sent during the build-up of the function
candidates table once for each set of powers in
variables. Notice, that the argument array contains the powers
PLUS ONE. For example, to De select the function
f = x1^2 * x2^4 * x3^5,
this method should return kFALSE if given the argument
{ 3, 4, 6 }
Set the max angle (in degrees) between the initial data vector to be fitted, and the new candidate function to be included in the fit. By default it is 0, which automatically chooses another selection criteria. See alsoclass description
Set the min angle (in degrees) between a new candidate function and the subspace spanned by the previously accepted functions. See alsoclass description
Define a user function. The input array must be of the form (p11, ..., p1N, ... ,pL1, ..., pLN) Where N is the dimension of the data sample, L is the number of terms (given in terms) and the first number, labels the term, the second the variable. More information is given in theclass description
Set the user parameter for the function selection. The bigger the limit, the more functions are used. The meaning of this variable is defined in theclass description
Set the acceptable relative error for when sum of square residuals is considered minimized. For a full account, refer to theclass description
PRIVATE METHOD: Test whether the currently considered function contributes to the fit. See alsoclass description
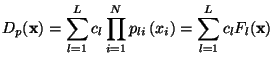
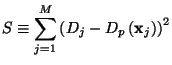
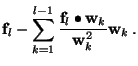
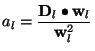
![$\displaystyle S_l = \left[\mathbf{D} - \sum^l_{k=1} a_k\mathbf{w}_k\right]^2 = ...
...2 - 2\mathbf{D} \sum^l_{k=1} a_k\mathbf{w}_k + \sum^l_{k=1} a_k^2\mathbf{w}_k^2$](gif/multidimfit_img70.gif)
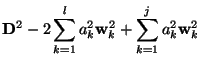
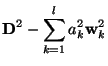
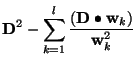
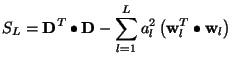
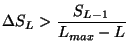
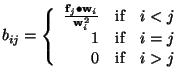
![$\displaystyle \mathbf{c} = \left(\mathsf{B}^{-1}\mathbf{a}\right) = \left[\mathbf{a}^T\left(\mathsf{B}^{-1}\right)^T\right]^T .$](gif/multidimfit_img97.gif)