Quick Links: ROOT Homepage Class Index Class Hierarchy

Source: header file source file viewVC header viewVC source

Sections: class description function members data members class charts

ROOT » HIST » HISTPAINTER » TGraphPainter

class TGraphPainter: public TVirtualGraphPainter

The graph painter class

Introduction
Graphs' plotting options
Exclusion graphs
Graphs with error bars

TGraphErrors
TGraphAsymmErrors
TGraphBentErrors

TGraphPolar options

Introduction

Graphs are drawn via the painter TGraphPainter class. This class implements techniques needed to display the various kind of graphs i.e.: TGraph, TGraphErrors, TGraphBentErrors and TGraphAsymmErrors.

To draw a graph "graph" it's enough to do:

   graph->Draw("AL");

The option "AL" in the Draw() method means:

The axis should be drawn (option "A"),
The graph should be drawn as a simple line (option "L").

By default a graph is drawn in the current pad in the current coordinate system. To define a suitable coordinate system and draw the axis the option "A" must be specified.

TGraphPainter offers many options to paint the various kind of graphs.

It is separated from the graph classes so that one can have graphs without the graphics overhead, for example in a batch program.

When a displayed graph is modified, there is no need to call Draw() again; the image will be refreshed the next time the pad will be updated.

A pad is updated after one of these three actions:

a carriage return on the ROOT command line,
a click inside the pad,
a call to TPad::Update.

Graphs' plotting options

Graphs can be drawn with the following options:

"A"	Axis are drawn around the graph
"L"	A simple polyline is drawn
"F"	A fill area is drawn ('CF' draw a smoothed fill area)
"C"	A smooth Curve is drawn
"*"	A Star is plotted at each point
"P"	The current marker is plotted at each point
"B"	A Bar chart is drawn
"1"	When a graph is drawn as a bar chart, this option makes the bars start from the bottom of the pad. By default they start at 0.
"X+"	The X-axis is drawn on the top side of the plot.
"Y+"	The Y-axis is drawn on the right side of the plot.

Drawing options can be combined. In the following example the graph is drawn as a smooth curve (option "C") with markers (option "P") and with axes (option "A").

Picture Source

{
   TCanvas *c1 = new TCanvas("c1","c1",200,10,600,400);

   c1->SetFillColor(42);
   c1->SetGrid();

   const Int_t n = 20;
   Double_t x[n], y[n];
   for (Int_t i=0;i<n;i++) {
      x[i] = i*0.1;
      y[i] = 10*sin(x[i]+0.2);
   }
   gr = new TGraph(n,x,y);
   gr->SetLineColor(2);
   gr->SetLineWidth(4);
   gr->SetMarkerColor(4);
   gr->SetMarkerSize(1.5);
   gr->SetMarkerStyle(21);
   gr->SetTitle("Option ACP example");
   gr->GetXaxis()->SetTitle("X title");
   gr->GetYaxis()->SetTitle("Y title");
   gr->Draw("ACP");

   // TCanvas::Update() draws the frame, after which one can change it
   c1->Update();
   c1->GetFrame()->SetFillColor(21);
   c1->GetFrame()->SetBorderSize(12);
   c1->Modified();
   return c1;
}

The following macro shows the option "B" usage. It can be combined with the option "1".

Picture Source

{
   TCanvas *c47 = new TCanvas("c47","c47",200,10,600,400);
   c47->Divide(1,2);
   const Int_t n = 20;
   Double_t x[n], y[n];
   for (Int_t i=0;i<n;i++) {
      x[i] = i*0.1;
      y[i] = 10*sin(x[i]+0.2)-6;
   }
   gr = new TGraph(n,x,y);
   gr->SetFillColor(38);
   c47->cd(1); gr->Draw("AB");
   c47->cd(2); gr->Draw("AB1");
 return c47;
}

Exclusion graphs

When a graph is painted with the option "C" or "L" it is possible to draw a filled area on one side of the line. This is useful to show exclusion zones.

This drawing mode is activated when the absolute value of the graph line width (set by SetLineWidth()) is greater than 99. In that case the line width number is interpreted as:

      100*ff+ll = ffll

The two digits number "ll" represent the normal line width
The two digits number "ff" represent the filled area width.
The sign of "ffll" allows to flip the filled area from one side of the line to the other.

The current fill area attributes are used to draw the hatched zone.

Picture Source

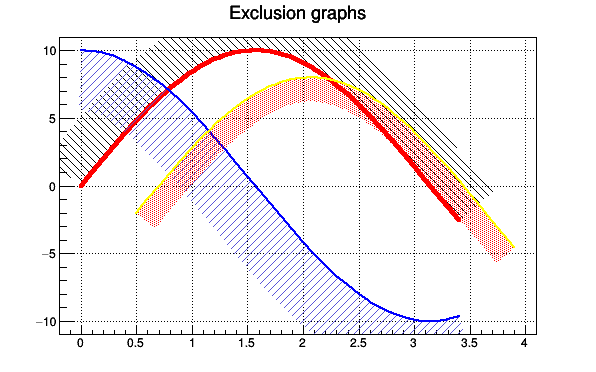
TCanvas *exclusiongraph() {
   // Draw three graphs with an exclusion zone.
   //Author: Olivier Couet
   
   TCanvas *c1 = new TCanvas("c1","Exclusion graphs examples",200,10,600,400);
   c1->SetGrid();

   TMultiGraph *mg = new TMultiGraph();
   mg->SetTitle("Exclusion graphs");

   const Int_t n = 35;
   Double_t x1[n], x2[n], x3[n], y1[n], y2[n], y3[n];
   for (Int_t i=0;i<n;i++) {
     x1[i]  = i*0.1;
     x2[i]  = x1[i];
     x3[i]  = x1[i]+.5;
     y1[i] = 10*sin(x1[i]);
     y2[i] = 10*cos(x1[i]);
     y3[i] = 10*sin(x1[i])-2;
   }

   TGraph *gr1 = new TGraph(n,x1,y1);
   gr1->SetLineColor(2);
   gr1->SetLineWidth(1504);
   gr1->SetFillStyle(3005);

   TGraph *gr2 = new TGraph(n,x2,y2);
   gr2->SetLineColor(4);
   gr2->SetLineWidth(-2002);
   gr2->SetFillStyle(3004);
   gr2->SetFillColor(9);

   TGraph *gr3 = new TGraph(n,x3,y3);
   gr3->SetLineColor(5);
   gr3->SetLineWidth(-802);
   gr3->SetFillStyle(3002);
   gr3->SetFillColor(2);

   mg->Add(gr1);
   mg->Add(gr2);
   mg->Add(gr3);
   mg->Draw("AC");

   return c1;
}

Graphs with error bars

Three classes are available to handle graphs with error bars: TGraphErrors, TGraphAsymmErrors and TGraphBentErrors. The following drawing options are specific to graphs with error bars:

"Z"	Do not draw small horizontal and vertical lines the end of the error bars. Without "Z", the default is to draw these.
">"	An arrow is drawn at the end of the error bars. The size of the arrow is set to 2/3 of the marker size.
"\|>"	A filled arrow is drawn at the end of the error bars. The size of the arrow is set to 2/3 of the marker size.
"X"	Do not draw error bars. By default, graph classes that have errors are drawn with the errors (TGraph itself has no errors, and so this option has no effect.)
"\|\|"	Draw only the small vertical/horizontal lines at the ends of the error bars, without drawing the bars themselves. This option is interesting to superimpose statistical-only errors on top of a graph with statistical+systematic errors.
"[]"	Does the same as option "\|\|" except that it draws additional marks at the ends of the small vertical/horizontal lines. It makes plots less ambiguous in case several graphs are drawn on the same picture.
"0"	By default, when a data point is outside the visible range along the Y axis, the error bars are not drawn. This option forces error bars' drawing for the data points outside the visible range along the Y axis (see example below).
"2"	Error rectangles are drawn.
"3"	A filled area is drawn through the end points of the vertical error bars.
"4"	A smoothed filled area is drawn through the end points of the vertical error bars.
"5"	Error rectangles are drawn like option "2". In addition the contour line around the boxes is drawn. This can be useful when boxes' fill colors are very light or in gray scale mode.

gStyle->SetErrorX(dx) controls the size of the error along x. dx = 0 removes the error along x.

gStyle->SetEndErrorSize(np) controls the size of the lines at the end of the error bars (when option 1 is used). By default np=1. (np represents the number of pixels).

TGraphErrors

A TGraphErrors is a TGraph with error bars. The errors are defined along X and Y and are symmetric: The left and right errors are the same along X and the bottom and up errors are the same along Y.

Picture Source

{
   TCanvas *c4 = new TCanvas("c4","c4",200,10,600,400);
   double x[] = {0, 1, 2, 3, 4};
   double y[] = {0, 2, 4, 1, 3};
   double ex[] = {0.1, 0.2, 0.3, 0.4, 0.5};
   double ey[] = {1, 0.5, 1, 0.5, 1};
   TGraphErrors* ge = new TGraphErrors(5, x, y, ex, ey);
   ge->Draw("ap");
   return c4;
}

The option "0" shows the error bars for data points outside range.

Picture Source

{
   TCanvas *c48 = new TCanvas("c48","c48",200,10,600,400);
   float x[]     = {1,2,3};
   float err_x[] = {0,0,0};
   float err_y[] = {5,5,5};
   float y[]     = {1,4,9};
   TGraphErrors tg(3,x,y,err_x,err_y);
   c48->Divide(2,1);
   c48->cd(1); gPad->DrawFrame(0,0,4,8); tg.Draw("PC");
   c48->cd(2); gPad->DrawFrame(0,0,4,8); tg.Draw("0PC");
   return c48;
}

The option "3" shows the errors as a band.

Picture Source

{
   TCanvas *c41 = new TCanvas("c41","c41",200,10,600,400);
   double x[] = {0, 1, 2, 3, 4};
   double y[] = {0, 2, 4, 1, 3};
   double ex[] = {0.1, 0.2, 0.3, 0.4, 0.5};
   double ey[] = {1, 0.5, 1, 0.5, 1};
   TGraphErrors* ge = new TGraphErrors(5, x, y, ex, ey);
   ge->SetFillColor(4);
   ge->SetFillStyle(3010);
   ge->Draw("a3");
   return c41;
}

The option "4" is similar to the option "3" except that the band is smoothed. As the following picture shows, this option should be used carefully because the smoothing algorithm may show some (huge) "bouncing" effects. In some cases it looks nicer than option "3" (because it is smooth) but it can be misleading.

Picture Source

{
   TCanvas *c42 = new TCanvas("c42","c42",200,10,600,400);
   double x[] = {0, 1, 2, 3, 4};
   double y[] = {0, 2, 4, 1, 3};
   double ex[] = {0.1, 0.2, 0.3, 0.4, 0.5};
   double ey[] = {1, 0.5, 1, 0.5, 1};
   TGraphErrors* ge = new TGraphErrors(5, x, y, ex, ey);
   ge->SetFillColor(6);
   ge->SetFillStyle(3005);
   ge->Draw("a4");
   return c42;
}

The following example shows how the option "[]" can be used to superimpose systematic errors on top of a graph with statistical errors.

Picture Source

{
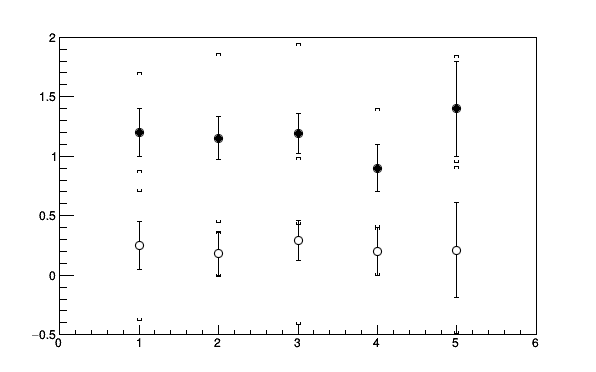
   TCanvas *c43 = new TCanvas("c43","c43",200,10,600,400);
   c43->DrawFrame(0., -0.5, 6., 2);

   double x[5]    = {1, 2, 3, 4, 5};
   double zero[5] = {0, 0, 0, 0, 0};

   // data set (1) with stat and sys errors
   double py1[5]      = {1.2, 1.15, 1.19, 0.9, 1.4};
   double ey_stat1[5] = {0.2, 0.18, 0.17, 0.2, 0.4};
   double ey_sys1[5]  = {0.5, 0.71, 0.76, 0.5, 0.45};

   // data set (2) with stat and sys errors
   double y2[5]       = {0.25, 0.18, 0.29, 0.2, 0.21};
   double ey_stat2[5] = {0.2, 0.18, 0.17, 0.2, 0.4};
   double ey_sys2[5]  = {0.63, 0.19, 0.7, 0.2, 0.7};

   // Now draw data set (1)

   // We first have to draw it only with the stat errors
   TGraphErrors *graph1 = new TGraphErrors(5, x, py1, zero, ey_stat1);
   graph1->SetMarkerStyle(20);
   graph1->Draw("P");

   // Now we have to somehow depict the sys errors

   TGraphErrors *graph1_sys = new TGraphErrors(5, x, py1, zero, ey_sys1);
   graph1_sys->Draw("[]");

   // Now draw data set (2)

   // We first have to draw it only with the stat errors
   TGraphErrors *graph2 = new TGraphErrors(5, x, y2, zero, ey_stat2);
   graph2->SetMarkerStyle(24);
   graph2->Draw("P");

   // Now we have to somehow depict the sys errors

   TGraphErrors *graph2_sys = new TGraphErrors(5, x, y2, zero, ey_sys2);
   graph2_sys->Draw("[]");
   return c43;
}

TGraphAsymmErrors

A TGraphAsymmErrors is like a TGraphErrors but the errors defined along X and Y are not symmetric: The left and right errors are different along X and the bottom and up errors are different along Y.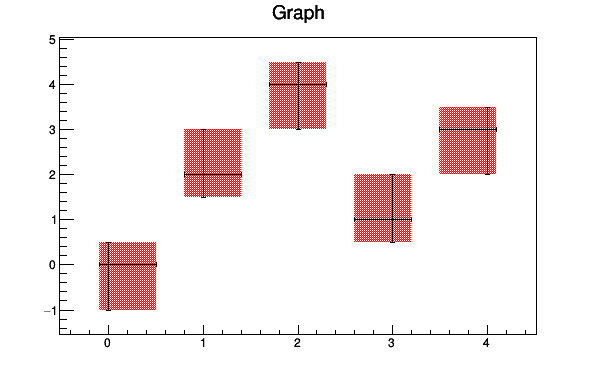

Picture Source

{
   TCanvas *c44 = new TCanvas("c44","c44",200,10,600,400);
   double ax[] = {0, 1, 2, 3, 4};
   double ay[] = {0, 2, 4, 1, 3};
   double aexl[] = {0.1, 0.2, 0.3, 0.4, 0.5};
   double aexh[] = {0.5, 0.4, 0.3, 0.2, 0.1};
   double aeyl[] = {1, 0.5, 1, 0.5, 1};
   double aeyh[] = {0.5, 1, 0.5, 1, 0.5};
   TGraphAsymmErrors* gae = new TGraphAsymmErrors(5, ax, ay, aexl, aexh, aeyl, aeyh);
   gae->SetFillColor(2);
   gae->SetFillStyle(3001);
   gae->Draw("a2");
   gae->Draw("p");
   return c44;
}

TGraphBentErrors

A TGraphBentErrors is like a TGraphAsymmErrors. An extra parameter allows to bend the error bars to better see them when several graphs are drawn on the same plot.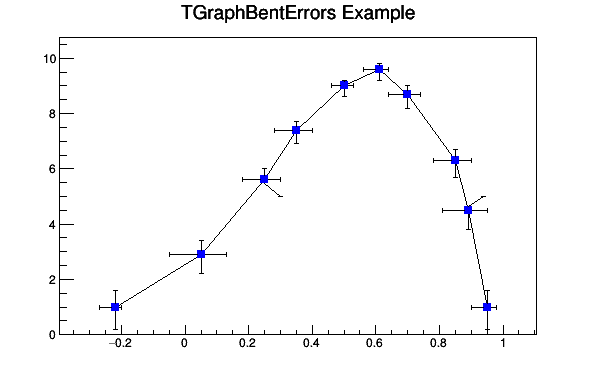

Picture Source

{
   TCanvas *c45 = new TCanvas("c45","c45",200,10,600,400);
   const Int_t n = 10;
   Double_t x[n]  = {-0.22, 0.05, 0.25, 0.35, 0.5, 0.61,0.7,0.85,0.89,0.95};
   Double_t y[n]  = {1,2.9,5.6,7.4,9,9.6,8.7,6.3,4.5,1};
   Double_t exl[n] = {.05,.1,.07,.07,.04,.05,.06,.07,.08,.05};
   Double_t eyl[n] = {.8,.7,.6,.5,.4,.4,.5,.6,.7,.8};
   Double_t exh[n] = {.02,.08,.05,.05,.03,.03,.04,.05,.06,.03};
   Double_t eyh[n] = {.6,.5,.4,.3,.2,.2,.3,.4,.5,.6};
   Double_t exld[n] = {.0,.0,.0,.0,.0,.0,.0,.0,.0,.0};
   Double_t eyld[n] = {.0,.0,.05,.0,.0,.0,.0,.0,.0,.0};
   Double_t exhd[n] = {.0,.0,.0,.0,.0,.0,.0,.0,.0,.0};
   Double_t eyhd[n] = {.0,.0,.0,.0,.0,.0,.0,.0,.05,.0};
   TGraphBentErrors *gr = new TGraphBentErrors(n,x,y,exl,exh,eyl,eyh,exld,exhd,eyld,eyhd);
   gr->SetTitle("TGraphBentErrors Example");
   gr->SetMarkerColor(4);
   gr->SetMarkerStyle(21);
   gr->Draw("ALP");
   return c45;
}

TGraphPolar options

The drawing options for the polar graphs are the following:

"O"	Polar labels are drawn orthogonally to the polargram radius.
"P"	Polymarker are drawn at each point position.
"E"	Draw error bars.
"F"	Draw fill area (closed polygon).
"A"	Force axis redrawing even if a polargram already exists.
"N"	Disable the display of the polar labels.

Picture Source

{
   TCanvas *c46 = new TCanvas("c46","c46",500,500);
   TGraphPolar * grP1 = new TGraphPolar();
   grP1->SetTitle("TGraphPolar example");

   grP1->SetPoint(0, (1*TMath::Pi())/4., 0.05);
   grP1->SetPoint(1, (2*TMath::Pi())/4., 0.10);
   grP1->SetPoint(2, (3*TMath::Pi())/4., 0.15);
   grP1->SetPoint(3, (4*TMath::Pi())/4., 0.20);
   grP1->SetPoint(4, (5*TMath::Pi())/4., 0.25);
   grP1->SetPoint(5, (6*TMath::Pi())/4., 0.30);
   grP1->SetPoint(6, (7*TMath::Pi())/4., 0.35);
   grP1->SetPoint(7, (8*TMath::Pi())/4., 0.40);

   grP1->SetMarkerStyle(20);
   grP1->SetMarkerSize(1.);
   grP1->SetMarkerColor(4);
   grP1->SetLineColor(4);
   grP1->Draw("ALP");

   // Update, otherwise GetPolargram returns 0
   c46->Update();
   grP1->GetPolargram()->SetToRadian();

   return c46;
}

Function Members (Methods)

public:

	TGraphPainter()
	TGraphPainter(const TGraphPainter&)
virtual	~TGraphPainter()
void	TObject::AbstractMethod(const char* method) const
virtual void	TObject::AppendPad(Option_t* option = "")
virtual void	TObject::Browse(TBrowser* b)
static TClass*	Class()
virtual const char*	TObject::ClassName() const
virtual void	TObject::Clear(Option_t* = "")
virtual TObject*	TObject::Clone(const char* newname = "") const
virtual Int_t	TObject::Compare(const TObject* obj) const
void	ComputeLogs(Int_t npoints, Int_t opt)
virtual void	TObject::Copy(TObject& object) const
virtual void	TObject::Delete(Option_t* option = "")MENU
virtual Int_t	TObject::DistancetoPrimitive(Int_t px, Int_t py)
virtual Int_t	DistancetoPrimitiveHelper(TGraph* theGraph, Int_t px, Int_t py)
virtual void	TObject::Draw(Option_t* option = "")
virtual void	TObject::DrawClass() constMENU
virtual TObject*	TObject::DrawClone(Option_t* option = "") constMENU
virtual void	DrawPanelHelper(TGraph* theGraph)
virtual void	TObject::Dump() constMENU
virtual void	TObject::Error(const char* method, const char* msgfmt) const
virtual void	TObject::Execute(const char* method, const char* params, Int_t* error = 0)
virtual void	TObject::Execute(TMethod* method, TObjArray* params, Int_t* error = 0)
virtual void	TObject::ExecuteEvent(Int_t event, Int_t px, Int_t py)
virtual void	ExecuteEventHelper(TGraph* theGraph, Int_t event, Int_t px, Int_t py)
virtual void	TObject::Fatal(const char* method, const char* msgfmt) const
virtual TObject*	TObject::FindObject(const char* name) const
virtual TObject*	TObject::FindObject(const TObject* obj) const
virtual Option_t*	TObject::GetDrawOption() const
static Long_t	TObject::GetDtorOnly()
virtual const char*	TObject::GetIconName() const
virtual const char*	TObject::GetName() const
virtual char*	TObject::GetObjectInfo(Int_t px, Int_t py) const
virtual char*	GetObjectInfoHelper(TGraph* theGraph, Int_t px, Int_t py) const
static Bool_t	TObject::GetObjectStat()
virtual Option_t*	TObject::GetOption() const
static TVirtualGraphPainter*	TVirtualGraphPainter::GetPainter()
virtual const char*	TObject::GetTitle() const
virtual UInt_t	TObject::GetUniqueID() const
virtual Bool_t	TObject::HandleTimer(TTimer* timer)
virtual ULong_t	TObject::Hash() const
virtual void	TObject::Info(const char* method, const char* msgfmt) const
virtual Bool_t	TObject::InheritsFrom(const char* classname) const
virtual Bool_t	TObject::InheritsFrom(const TClass* cl) const
virtual void	TObject::Inspect() constMENU
void	TObject::InvertBit(UInt_t f)
virtual TClass*	IsA() const
virtual Bool_t	TObject::IsEqual(const TObject* obj) const
virtual Bool_t	TObject::IsFolder() const
Bool_t	TObject::IsOnHeap() const
virtual Bool_t	TObject::IsSortable() const
Bool_t	TObject::IsZombie() const
virtual void	TObject::ls(Option_t* option = "") const
void	TObject::MayNotUse(const char* method) const
virtual Bool_t	TObject::Notify()
void	TObject::Obsolete(const char* method, const char* asOfVers, const char* removedFromVers) const
static void	TObject::operator delete(void* ptr)
static void	TObject::operator delete(void* ptr, void* vp)
static void	TObject::operator delete[](void* ptr)
static void	TObject::operator delete[](void* ptr, void* vp)
void*	TObject::operator new(size_t sz)
void*	TObject::operator new(size_t sz, void* vp)
void*	TObject::operator new[](size_t sz)
void*	TObject::operator new[](size_t sz, void* vp)
TGraphPainter&	operator=(const TGraphPainter&)
virtual void	TObject::Paint(Option_t* option = "")
virtual void	PaintGraph(TGraph* theGraph, Int_t npoints, const Double_t* x, const Double_t* y, Option_t* chopt)
void	PaintGraphAsymmErrors(TGraph* theGraph, Option_t* option)
void	PaintGraphBentErrors(TGraph* theGraph, Option_t* option)
void	PaintGraphErrors(TGraph* theGraph, Option_t* option)
virtual void	PaintGrapHist(TGraph* theGraph, Int_t npoints, const Double_t* x, const Double_t* y, Option_t* chopt)
void	PaintGraphPolar(TGraph* theGraph, Option_t* option)
void	PaintGraphQQ(TGraph* theGraph, Option_t* option)
void	PaintGraphSimple(TGraph* theGraph, Option_t* option)
virtual void	PaintHelper(TGraph* theGraph, Option_t* option)
void	PaintPolyLineHatches(TGraph* theGraph, Int_t n, const Double_t* x, const Double_t* y)
virtual void	PaintStats(TGraph* theGraph, TF1* fit)
virtual void	TObject::Pop()
virtual void	TObject::Print(Option_t* option = "") const
virtual Int_t	TObject::Read(const char* name)
virtual void	TObject::RecursiveRemove(TObject* obj)
void	TObject::ResetBit(UInt_t f)
virtual void	TObject::SaveAs(const char* filename = "", Option_t* option = "") constMENU
virtual void	TObject::SavePrimitive(ostream& out, Option_t* option = "")
void	TObject::SetBit(UInt_t f)
void	TObject::SetBit(UInt_t f, Bool_t set)
virtual void	TObject::SetDrawOption(Option_t* option = "")MENU
static void	TObject::SetDtorOnly(void* obj)
static void	TObject::SetObjectStat(Bool_t stat)
static void	TVirtualGraphPainter::SetPainter(TVirtualGraphPainter* painter)
virtual void	TObject::SetUniqueID(UInt_t uid)
virtual void	ShowMembers(TMemberInspector&)
void	Smooth(TGraph* theGraph, Int_t npoints, Double_t* x, Double_t* y, Int_t drawtype)
virtual void	Streamer(TBuffer&)
void	StreamerNVirtual(TBuffer& ClassDef_StreamerNVirtual_b)
virtual void	TObject::SysError(const char* method, const char* msgfmt) const
Bool_t	TObject::TestBit(UInt_t f) const
Int_t	TObject::TestBits(UInt_t f) const
virtual void	TObject::UseCurrentStyle()
virtual void	TObject::Warning(const char* method, const char* msgfmt) const
virtual Int_t	TObject::Write(const char* name = 0, Int_t option = 0, Int_t bufsize = 0)
virtual Int_t	TObject::Write(const char* name = 0, Int_t option = 0, Int_t bufsize = 0) const

protected:

virtual void	TObject::DoError(int level, const char* location, const char* fmt, va_list va) const
void	TObject::MakeZombie()

Data Members

public:

enum TObject::EStatusBits {	kCanDelete
	kMustCleanup
	kObjInCanvas
	kIsReferenced
	kHasUUID
	kCannotPick
	kNoContextMenu
	kInvalidObject
};
enum TObject::[unnamed] {	kIsOnHeap
	kNotDeleted
	kZombie
	kBitMask
	kSingleKey
	kOverwrite
	kWriteDelete
};

Class Charts

Inheritance Inherited Members Includes Libraries

Function documentation

TGraphPainter()

Default constructor

~TGraphPainter()

Destructor.

void ComputeLogs(Int_t npoints, Int_t opt)

Compute the logarithm of global variables gxwork and gywork according to the value of Options and put the results in the global variables gxworkl and gyworkl.

npoints : Number of points in gxwork and in gywork.

opt = 1 ComputeLogs is called from PaintGrapHist
opt = 0 ComputeLogs is called from PaintGraph

Int_t DistancetoPrimitiveHelper(TGraph* theGraph, Int_t px, Int_t py)

Compute distance from point px,py to a graph.

Compute the closest distance of approach from point px,py to this line. The distance is computed in pixels units.

void DrawPanelHelper(TGraph* theGraph)

Display a panel with all histogram drawing options.

void ExecuteEventHelper(TGraph* theGraph, Int_t event, Int_t px, Int_t py)

Execute action corresponding to one event.

This member function is called when a graph is clicked with the locator.

If the left mouse button is clicked on one of the line end points, this point follows the cursor until button is released.

If the middle mouse button clicked, the line is moved parallel to itself until the button is released.

char * GetObjectInfoHelper(TGraph* theGraph, Int_t px, Int_t py) const

void PaintHelper(TGraph* theGraph, Option_t* option)

Paint a any kind of TGraph

void PaintGraph(TGraph* theGraph, Int_t npoints, const Double_t* x, const Double_t* y, Option_t* chopt)

Control function to draw a graph.

void PaintGrapHist(TGraph* theGraph, Int_t npoints, const Double_t* x, const Double_t* y, Option_t* chopt)

This is a service method used by THistPainter to paint 1D histograms. It is not used to paint TGraph.

Input parameters:

npoints : Number of points in X or in Y.
x[npoints] or x[0] : x coordinates or (xmin,xmax).
y[npoints] or y[0] : y coordinates or (ymin,ymax).
chopt : Option.

The aspect of the histogram is done according to the value of the chopt.

"R"	Graph is drawn horizontaly, parallel to X axis. (default is vertically, parallel to Y axis) If option R is selected the user must give: 2 values for Y (y[0]=YMIN and y[1]=YMAX) N values for X, one for each channel. Otherwise the user must give: N values for Y, one for each channel. 2 values for X (x[0]=XMIN and x[1]=XMAX)
"L"	A simple polyline beetwen every points is drawn.
"H"	An Histogram with equidistant bins is drawn as a polyline.
"F"	An histogram with equidistant bins is drawn as a fill area. Contour is not drawn unless chopt='H' is also selected..
"N"	Non equidistant bins (default is equidistant). If N is the number of channels array X and Y must be dimensionned as follow: >If option R is not selected (default) then the user must give: (N+1) values for X (limits of channels). N values for Y, one for each channel. Otherwise the user must give: (N+1) values for Y (limits of channels). N values for X, one for each channel.
"F1"	Idem as 'F' except that fill area base line is the minimum of the pad instead of Y=0.
"F2"	Draw a Fill area polyline connecting the center of bins
"C"	A smooth Curve is drawn.
"*"	A Star is plotted at the center of each bin.
"P"	Idem with the current marker.
"P0"	Idem with the current marker. Empty bins also drawn.
"B"	A Bar chart with equidistant bins is drawn as fill areas (Contours are drawn).
"]["	"Cutoff" style. When this option is selected together with H option, the first and last vertical lines of the histogram are not drawn.

void PaintGraphAsymmErrors(TGraph* theGraph, Option_t* option)

Paint this TGraphAsymmErrors with its current attributes.

void PaintGraphBentErrors(TGraph* theGraph, Option_t* option)

Paint this TGraphBentErrors with its current attributes.

void PaintGraphErrors(TGraph* theGraph, Option_t* option)

Paint this TGraphErrors with its current attributes.

void PaintGraphPolar(TGraph* theGraph, Option_t* option)

Paint this TGraphPolar with its current attributes.

void PaintGraphQQ(TGraph* theGraph, Option_t* option)

Paint this graphQQ. No options for the time being.

void PaintGraphSimple(TGraph* theGraph, Option_t* option)

Paint a simple graph, without errors bars.

void PaintPolyLineHatches(TGraph* theGraph, Int_t n, const Double_t* x, const Double_t* y)

Paint a polyline with hatches on one side showing an exclusion zone. x and y are the the vectors holding the polyline and n the number of points in the polyline and w the width of the hatches. w can be negative. This method is not meant to be used directly. It is called automatically according to the line style convention.

void PaintStats(TGraph* theGraph, TF1* fit)

Paint the statistics box with the fit info.

void Smooth(TGraph* theGraph, Int_t npoints, Double_t* x, Double_t* y, Int_t drawtype)

Smooth a curve given by N points.

The original code is from an underlaying routine for Draw based on the CERN GD3 routine TVIPTE:

        Author - Marlow etc.   Modified by - P. Ward     Date -  3.10.1973

This method draws a smooth tangentially continuous curve through the sequence of data points P(I) I=1,N where P(I)=(X(I),Y(I)). The curve is approximated by a polygonal arc of short vectors. The data points can represent open curves, P(1) != P(N) or closed curves P(2) == P(N). If a tangential discontinuity at P(I) is required, then set P(I)=P(I+1). Loops are also allowed.

Reference Marlow and Powell, Harwell report No.R.7092.1972 MCCONALOGUE, Computer Journal VOL.13, NO4, NOV1970P p392 6

npoints : Number of data points.
x : Abscissa
y : Ordinate

TGraphPainter()