User class for performing function integration. It will use the Richards Method for function derivation in a given interval. This class is implemented from TF1::Derivate{,2,3}(). @ingroup Derivation
| ~RichardsonDerivator() | |
| double | Derivative1(double x) |
| double | Derivative2(double x) |
| double | Derivative3(double x) |
| double | Error() const |
| ROOT::Math::RichardsonDerivator | RichardsonDerivator() |
| ROOT::Math::RichardsonDerivator | RichardsonDerivator(const ROOT::Math::RichardsonDerivator&) |
| void | SetFunction(const ROOT::Math::IGenFunction&, double xmin, double xmax) |
| void | SetRelTolerance(double) |
Implementing VirtualIntegrator Interface Set the desired relative Error.
Implementing VirtualIntegratorOneDim Interface
Returns the first derivative of the function at point x,
computed by Richardson's extrapolation method (use 2 derivative estimates
to compute a third, more accurate estimation)
first, derivatives with steps h and h/2 are computed by central difference formulas
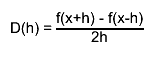the final estimate 
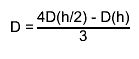"Numerical Methods for Scientists and Engineers", H.M.Antia, 2nd edition"
the argument eps may be specified to control the step size (precision).
the step size is taken as eps*(xmax-xmin).
the default value (0.001) should be good enough for the vast majority
of functions. Give a smaller value if your function has many changes
of the second derivative in the function range.
Getting the error via TF1::DerivativeError:
(total error = roundoff error + interpolation error)
the estimate of the roundoff error is taken as follows:
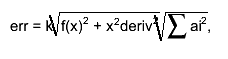where k is the double precision, ai are coefficients used in
central difference formulas
interpolation error is decreased by making the step size h smaller.
Returns the second derivative of the function at point x,
computed by Richardson's extrapolation method (use 2 derivative estimates
to compute a third, more accurate estimation)
first, derivatives with steps h and h/2 are computed by central difference formulas
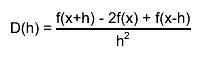the final estimate 
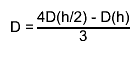"Numerical Methods for Scientists and Engineers", H.M.Antia, 2nd edition"
the argument eps may be specified to control the step size (precision).
the step size is taken as eps*(xmax-xmin).
the default value (0.001) should be good enough for the vast majority
of functions. Give a smaller value if your function has many changes
of the second derivative in the function range.
Getting the error via TF1::DerivativeError:
(total error = roundoff error + interpolation error)
the estimate of the roundoff error is taken as follows:
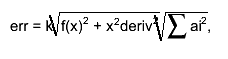where k is the double precision, ai are coefficients used in
central difference formulas
interpolation error is decreased by making the step size h smaller.
Returns the third derivative of the function at point x,
computed by Richardson's extrapolation method (use 2 derivative estimates
to compute a third, more accurate estimation)
first, derivatives with steps h and h/2 are computed by central difference formulas
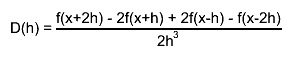the final estimate 
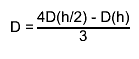"Numerical Methods for Scientists and Engineers", H.M.Antia, 2nd edition"
the argument eps may be specified to control the step size (precision).
the step size is taken as eps*(xmax-xmin).
the default value (0.001) should be good enough for the vast majority
of functions. Give a smaller value if your function has many changes
of the second derivative in the function range.
Getting the error via TF1::DerivativeError:
(total error = roundoff error + interpolation error)
the estimate of the roundoff error is taken as follows:
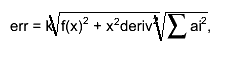where k is the double precision, ai are coefficients used in
central difference formulas
interpolation error is decreased by making the step size h smaller.
Set function to solve and the interval in where to look for the root.
\@param f Function to be minimized.
\@param xlow Lower bound of the search interval.
\@param xup Upper bound of the search interval.