zdemo.C File Reference

Detailed Description

This macro is an example of graphs in log scales with annotations.

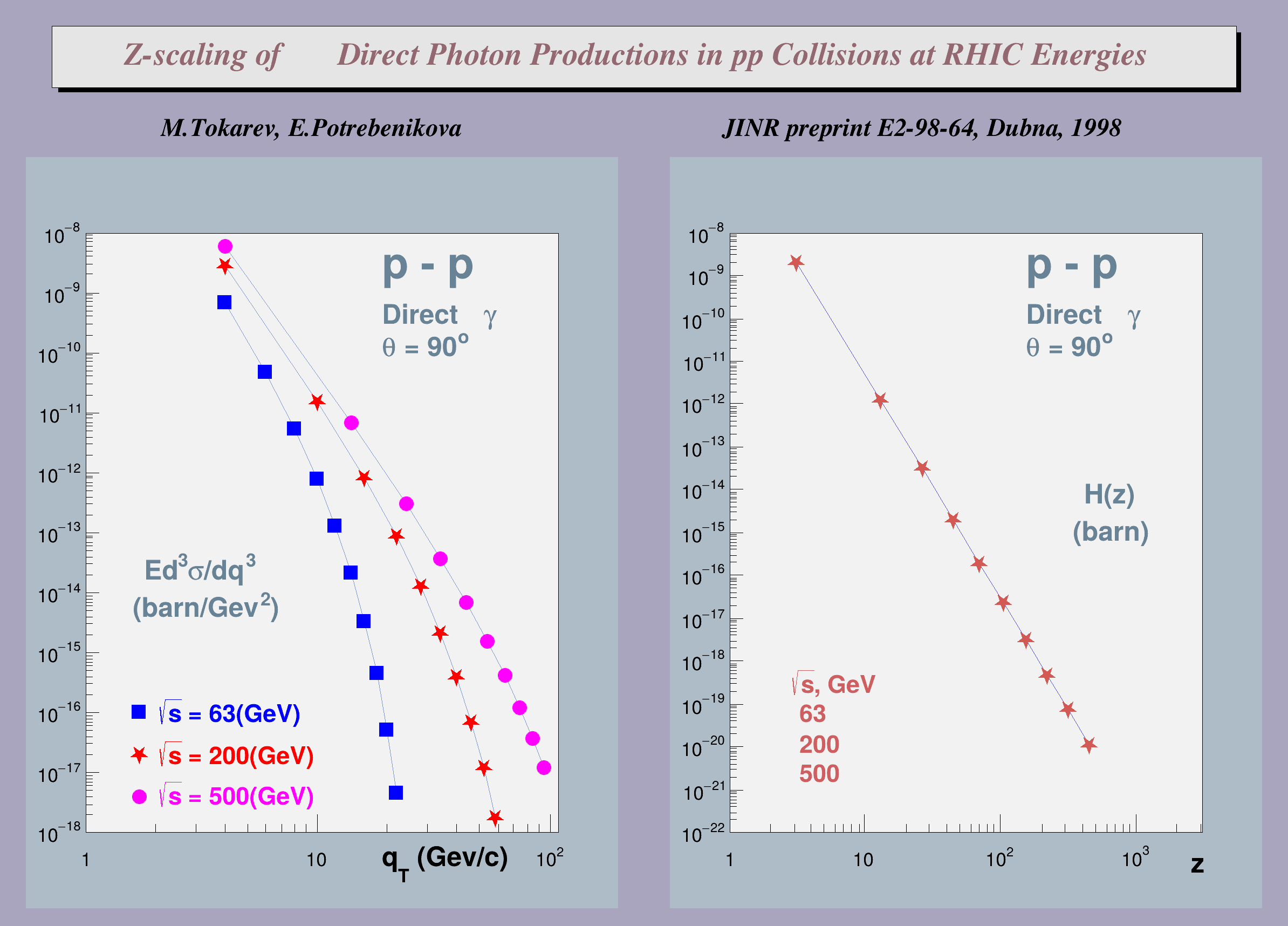
The presented results are predictions of invariant cross-section of Direct Photons produced at RHIC energies, based on the universality of scaling function H(z).

These Figures were published in JINR preprint E2-98-64, Dubna, 1998 and submitted to CPC.

Note that the way greek symbols, super/subscripts are obtained illustrate the current limitations of Root in this area.

 
#include "TCanvas.h"
#include "TPad.h"
#include "TPaveLabel.h"
#include "TLatex.h"
#include "TGraph.h"
#include "TFrame.h"
 
#ifdef HZ
#undef HZ
#endif
 
const Int_t NMAX = 20;
Int_t NLOOP;
Float_t Z[NMAX], HZ[NMAX], PT[NMAX], INVSIG[NMAX];
 
void hz_calc(Float_t, Float_t, Float_t, Float_t, Float_t, Float_t);
 
//__________________________________________________________________
void zdemo()
{
 
   Float_t energ;
   Float_t dens;
   Float_t tgrad;
   Float_t ptmin;
   Float_t ptmax;
   Float_t delp;
 
   // Create a new canvas.
   TCanvas *c1 = new TCanvas("zdemo",
      "Monte Carlo Study of Z scaling",10,40,800,600);
   c1->Range(0,0,25,18);
   c1->SetFillColor(40);
 
   TPaveLabel *pl = new TPaveLabel(1,16.3,24,17.5,"Z-scaling of \
      Direct Photon Productions in pp Collisions at RHIC Energies","br");
   pl->SetFillColor(18);
   pl->SetTextFont(32);
   pl->SetTextColor(49);
   pl->Draw();
 
   TLatex t0;
   t0.SetTextFont(32);
   t0.SetTextColor(1);
   t0.SetTextSize(0.03);
   t0.SetTextAlign(12);
   t0.DrawLatex(3.1,15.5,"M.Tokarev, E.Potrebenikova ");
   t0.DrawLatex(14.,15.5,"JINR preprint E2-98-64, Dubna, 1998 ");
 
   TPad *pad1 = new TPad("pad1","This is pad1",0.02,0.02,0.48,0.83,33);
   TPad *pad2 = new TPad("pad2","This is pad2",0.52,0.02,0.98,0.83,33);
 
   pad1->Draw();
   pad2->Draw();
 
//
// Cross-section of direct photon production in pp collisions
// at 500 GeV vs Pt
//
   energ = 63;
   dens  = 1.766;
   tgrad = 90.;
   ptmin = 4.;
   ptmax = 24.;
   delp  = 2.;
   hz_calc(energ, dens, tgrad, ptmin, ptmax, delp);
   pad1->cd();
   pad1->Range(-0.255174,-19.25,2.29657,-6.75);
   pad1->SetLogx();
   pad1->SetLogy();
 
   // create a 2-d histogram to define the range
   pad1->DrawFrame(1,1e-18,110,1e-8);
   pad1->GetFrame()->SetFillColor(19);
 
   TLatex t1;
   t1.SetNDC();
   t1.SetTextFont(62);
   t1.SetTextColor(36);
   t1.SetTextSize(0.08);
   t1.SetTextAlign(12);
   t1.DrawLatex(0.6,0.85,"p - p");
 
   t1.SetTextSize(0.05);
   t1.DrawLatex(0.6,0.79,"Direct #gamma");
   t1.DrawLatex(0.6,0.75,"#theta = 90^{o}");
 
   t1.DrawLatex(0.20,0.45,"Ed^{3}#sigma/dq^{3}");
   t1.DrawLatex(0.18,0.40,"(barn/Gev^{2})");
 
   t1.SetTextSize(0.045);
   t1.SetTextColor(kBlue);
   t1.DrawLatex(0.22,0.260,"#sqrt{s} = 63(GeV)");
   t1.SetTextColor(kRed);
   t1.DrawLatex(0.22,0.205,"#sqrt{s} = 200(GeV)");
   t1.SetTextColor(6);
   t1.DrawLatex(0.22,0.15,"#sqrt{s} = 500(GeV)");
 
   t1.SetTextSize(0.05);
   t1.SetTextColor(1);
   t1.DrawLatex(0.6,0.06,"q_{T} (Gev/c)");
 
   TGraph *gr1 = new TGraph(NLOOP,PT,INVSIG);
 
   gr1->SetLineColor(38);
   gr1->SetMarkerColor(kBlue);
   gr1->SetMarkerStyle(21);
   gr1->SetMarkerSize(1.1);
   gr1->Draw("LP");
 
//
// Cross-section of direct photon production in pp collisions
// at 200 GeV vs Pt
//
 
   energ = 200;
   dens  = 2.25;
   tgrad = 90.;
   ptmin = 4.;
   ptmax = 64.;
   delp  = 6.;
   hz_calc(energ, dens, tgrad, ptmin, ptmax, delp);
 
   TGraph *gr2 = new TGraph(NLOOP,PT,INVSIG);
   gr2->SetLineColor(38);
   gr2->SetMarkerColor(kRed);
   gr2->SetMarkerStyle(29);
   gr2->SetMarkerSize(1.5);
   gr2->Draw("LP");
 
//
// Cross-section of direct photon production in pp collisions
// at 500 GeV vs Pt
//
   energ = 500;
   dens  = 2.73;
   tgrad = 90.;
   ptmin = 4.;
   ptmax = 104.;
   delp  = 10.;
   hz_calc(energ, dens, tgrad, ptmin, ptmax, delp);
 
   TGraph *gr3 = new TGraph(NLOOP,PT,INVSIG);
 
   gr3->SetLineColor(38);
   gr3->SetMarkerColor(6);
   gr3->SetMarkerStyle(8);
   gr3->SetMarkerSize(1.1);
   gr3->Draw("LP");
 
   Float_t *dum = nullptr;
   TGraph *graph = new TGraph(1,dum,dum);
   graph->SetMarkerColor(kBlue);
   graph->SetMarkerStyle(21);
   graph->SetMarkerSize(1.1);
   graph->SetPoint(0,1.7,1.e-16);
   graph->Draw("LP");
 
   graph = new TGraph(1,dum,dum);
   graph->SetMarkerColor(kRed);
   graph->SetMarkerStyle(29);
   graph->SetMarkerSize(1.5);
   graph->SetPoint(0,1.7,2.e-17);
   graph->Draw("LP");
 
   graph = new TGraph(1,dum,dum);
   graph->SetMarkerColor(6);
   graph->SetMarkerStyle(8);
   graph->SetMarkerSize(1.1);
   graph->SetPoint(0,1.7,4.e-18);
   graph->Draw("LP");
 
   pad2->cd();
   pad2->Range(-0.43642,-23.75,3.92778,-6.25);
   pad2->SetLogx();
   pad2->SetLogy();
 
   pad2->DrawFrame(1,1e-22,3100,1e-8);
   pad2->GetFrame()->SetFillColor(19);
 
   TGraph *gr = new TGraph(NLOOP,Z,HZ);
   gr->SetTitle("HZ vs Z");
   gr->SetFillColor(19);
   gr->SetLineColor(9);
   gr->SetMarkerColor(50);
   gr->SetMarkerStyle(29);
   gr->SetMarkerSize(1.5);
   gr->Draw("LP");
 
   TLatex t2;
   t2.SetNDC();
   t2.SetTextFont(62);
   t2.SetTextColor(36);
   t2.SetTextSize(0.08);
   t2.SetTextAlign(12);
   t2.DrawLatex(0.6,0.85,"p - p");
 
   t2.SetTextSize(0.05);
   t2.DrawLatex(0.6,0.79,"Direct #gamma");
   t2.DrawLatex(0.6,0.75,"#theta = 90^{o}");
 
   t2.DrawLatex(0.70,0.55,"H(z)");
   t2.DrawLatex(0.68,0.50,"(barn)");
 
   t2.SetTextSize(0.045);
   t2.SetTextColor(46);
   t2.DrawLatex(0.20,0.30,"#sqrt{s}, GeV");
   t2.DrawLatex(0.22,0.26,"63");
   t2.DrawLatex(0.22,0.22,"200");
   t2.DrawLatex(0.22,0.18,"500");
 
   t2.SetTextSize(0.05);
   t2.SetTextColor(1);
   t2.DrawLatex(0.88,0.06,"z");
 
   c1->Modified();
   c1->Update();
}
 
void hz_calc(Float_t ENERG, Float_t DENS, Float_t TGRAD, Float_t PTMIN,
   Float_t PTMAX, Float_t DELP)
{
  Int_t I;
 
  Float_t GM1  = 0.00001;
  Float_t GM2  = 0.00001;
  Float_t A1   = 1.;
  Float_t A2   = 1.;
  Float_t ALX  = 2.;
  Float_t BETA = 1.;
  Float_t KF1  = 8.E-7;
  Float_t KF2  = 5.215;
 
  Float_t MN = 0.9383;
  Float_t DEGRAD=0.01745329;
 
  Float_t EB1, EB2, PB1, PB2, MB1, MB2, M1, M2;
  Float_t DNDETA;
 
  Float_t P1P2, P1P3, P2P3;
  Float_t Y1, Y2, S, SMIN,  SX1,  SX2, SX1X2, DELM;
  Float_t Y1X1,  Y1X2,   Y2X1,   Y2X2,   Y2X1X2,   Y1X1X2;
  Float_t KX1, KX2,  ZX1, ZX2;
  Float_t H1;
 
  Float_t PTOT, THET, ETOT, X1, X2;
 
  DNDETA= DENS;
  MB1   = MN*A1;
  MB2   = MN*A2;
  EB1   = ENERG/2.*A1;
  EB2   = ENERG/2.*A2;
  M1    = GM1;
  M2    = GM2;
  THET  = TGRAD*DEGRAD;
  NLOOP = (PTMAX-PTMIN)/DELP;
 
  for (I=0; I<NLOOP;I++) {
     PT[I]=PTMIN+I*DELP;
     PTOT = PT[I]/sin(THET);
 
     ETOT = sqrt(M1*M1 + PTOT*PTOT);
     PB1  = sqrt(EB1*EB1 - MB1*MB1);
     PB2  = sqrt(EB2*EB2 - MB2*MB2);
     P2P3 = EB2*ETOT+PB2*PTOT*cos(THET);
     P1P2 = EB2*EB1+PB2*PB1;
     P1P3 = EB1*ETOT-PB1*PTOT*cos(THET);
 
     X1 = P2P3/P1P2;
     X2 = P1P3/P1P2;
     Y1 = X1+sqrt(X1*X2*(1.-X1)/(1.-X2));
     Y2 = X2+sqrt(X1*X2*(1.-X2)/(1.-X1));
 
     S    = (MB1*MB1)+2.*P1P2+(MB2*MB2);
     SMIN = 4.*((MB1*MB1)*(X1*X1) +2.*X1*X2*P1P2+(MB2*MB2)*(X2*X2));
     SX1  = 4.*( 2*(MB1*MB1)*X1+2*X2*P1P2);
     SX2  = 4.*( 2*(MB2*MB2)*X2+2*X1*P1P2);
     SX1X2= 4.*(2*P1P2);
     DELM = pow((1.-Y1)*(1.-Y2),ALX);
 
     Z[I] = sqrt(SMIN)/DELM/pow(DNDETA,BETA);
 
     Y1X1  = 1. +X2*(1-2.*X1)/(2.*(Y1-X1)*(1.-X2));
     Y1X2  =     X1*(1-X1)/(2.*(Y1-X1)*(1.-X2)*(1.-X2));
     Y2X1  =     X2*(1-X2)/(2.*(Y2-X2)*(1.-X1)*(1.-X1));
     Y2X2  = 1. +X1*(1-2.*X2)/(2.*(Y2-X2)*(1.-X1));
     Y2X1X2= Y2X1*( (1.-2.*X2)/(X2*(1-X2)) -( Y2X2-1.)/(Y2-X2));
     Y1X1X2= Y1X2*( (1.-2.*X1)/(X1*(1-X1)) -( Y1X1-1.)/(Y1-X1));
 
     KX1=-DELM*(Y1X1*ALX/(1.-Y1) + Y2X1*ALX/(1.-Y2));
     KX2=-DELM*(Y2X2*ALX/(1.-Y2) + Y1X2*ALX/(1.-Y1));
     ZX1=Z[I]*(SX1/(2.*SMIN)-KX1/DELM);
     ZX2=Z[I]*(SX2/(2.*SMIN)-KX2/DELM);
 
     H1=ZX1*ZX2;
 
     HZ[I]=KF1/pow(Z[I],KF2);
     INVSIG[I]=(HZ[I]*H1*16.)/S;
 
  }
}

Authors

Michael Tokarev, Elena Potrebenikova (JINR Dubna)

Definition in file zdemo.C.