

Numeric algorithm tuning: caching of slow numeric integrals and parameterizations of slow numeric integrals
import sys
import ROOT
def getWorkspace(mode):
w = ROOT.RooWorkspace()
if mode != 2:
w = ROOT.RooWorkspace("w", 1)
w.factory(
"EXPR::model('1/((x-a)*(x-a)+0.01)+1/((y-a)*(y-a)+0.01)+1/((z-a)*(z-a)+0.01)',x[-1,1],y[-1,1],z[-1,1],a[-5,5])"
)
if mode == 1:
model = w["model"]
model.setStringAttribute("CACHEPARMINT", "x:y:z")
normSet = {w["x"], w["y"], w["z"]}
model.getVal(normSet)
w.writeToFile("rf903_numintcache.root")
if mode == 2:
f = ROOT.TFile("rf903_numintcache.root")
w = f.Get("w")
return w
mode = 0
w = getWorkspace(mode)
if mode == 1:
w.Print()
hhcache = w.expensiveObjectCache().getObj(1)
if hhcache:
ROOT.TCanvas("rf903_numintcache", "rf903_numintcache", 600, 600)
hhcache.createHistogram(
"a").
Draw()
else:
ROOT.RooFit.Error("rf903_numintcache", "Cached histogram is not existing in workspace")
sys.exit()
model = w["model"]
d = model.generate({w["x"], w["y"], w["z"]}, 1000)
model.fitTo(d, Verbose=True, Timer=True, PrintLevel=-1)
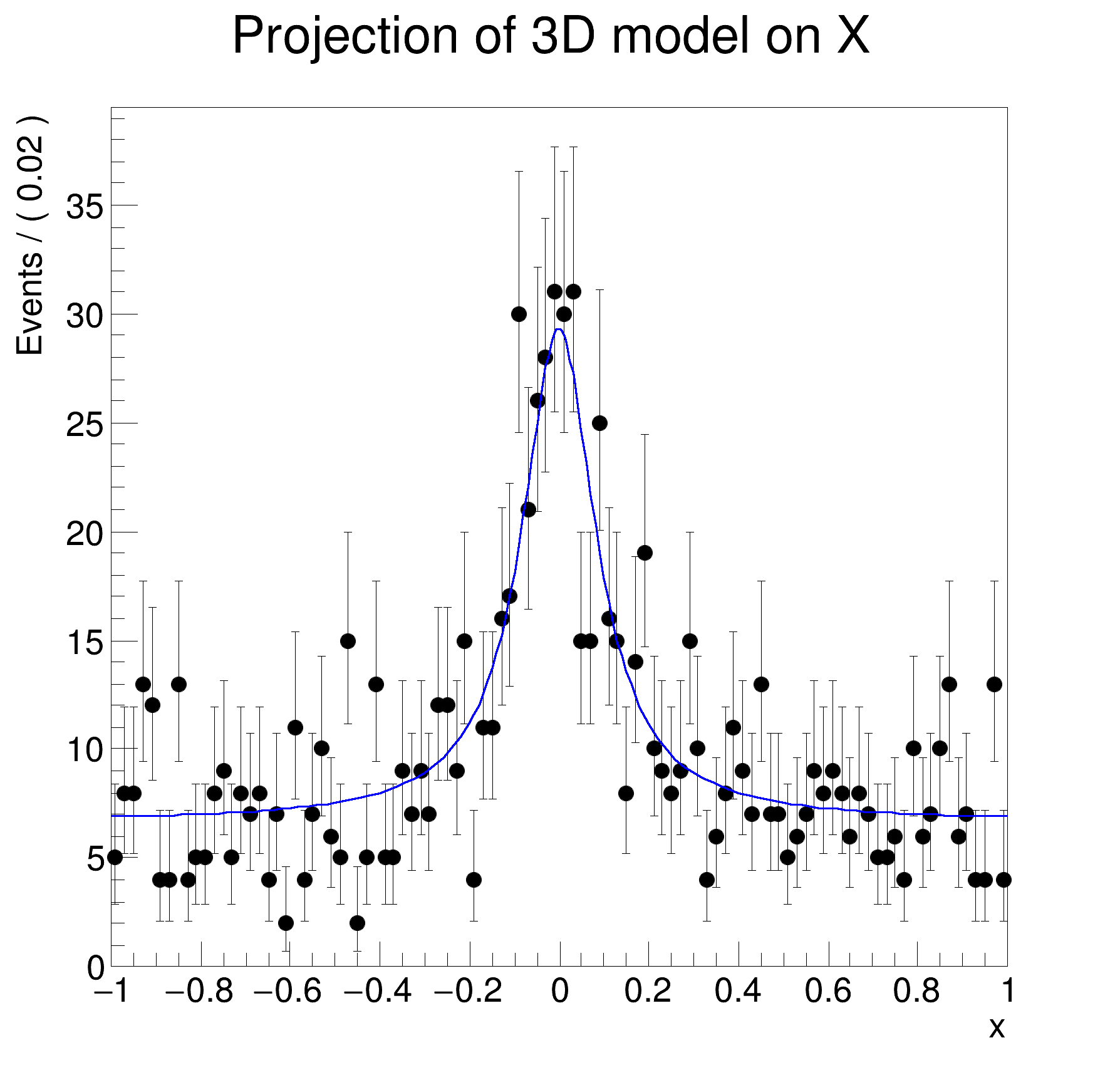
framex = w["x"].frame(Title="Projection of 3D model on X")
d.plotOn(framex)
model.plotOn(framex)
c = ROOT.TCanvas("rf903_numintcache", "rf903_numintcache", 600, 600)
framex.Draw()
c.SaveAs("rf903_numintcache.png")
ROOT.gDirectory.Add(w)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(model_Int[x,y,z]) using numeric integrator RooAdaptiveIntegratorND to calculate Int(x,y,z)
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: activating const optimization
[#0] WARNING:Minimization -- RooAbsMinimizerFcn::synchronize: WARNING: no initial error estimate available for a: using 1
prevFCN = 1659.930708 a=0.02833, [#1] INFO:NumericIntegration -- RooRealIntegral::init(model_Int[x,y,z]) using numeric integrator RooAdaptiveIntegratorND to calculate Int(x,y,z)
prevFCN = 1675.611563 a=-0.02833,
prevFCN = 1673.217894 a=0.002833,
prevFCN = 1660.205177 a=-0.002833,
prevFCN = 1659.94939 a=0.0002833,
prevFCN = 1659.944972 a=-0.0002833,
prevFCN = 1659.919376 a=-0.001237,
prevFCN = 1659.902781 a=-0.001089,
prevFCN = 1659.903175 a=-0.001384,
prevFCN = 1659.90318 a=-0.001237,
prevFCN = 1659.902781 a=-0.001089,
prevFCN = 1659.903175 a=-0.001384,
prevFCN = 1659.90318 a=-0.001207,
prevFCN = 1659.902797 a=-0.001266,
prevFCN = 1659.902798 [#1] INFO:Minimization -- Command timer: Real time 0:00:02, CP time 2.850
[#1] INFO:Minimization -- Session timer: Real time 0:00:02, CP time 2.850
a=-0.001237,
prevFCN = 1659.902781 a=-0.001207,
prevFCN = 1659.902797 a=-0.001266,
prevFCN = 1659.902798 a=-0.001231,
prevFCN = 1659.902782 a=-0.001243,
prevFCN = 1659.902782 [#1] INFO:Minimization -- Command timer: Real time 0:00:00, CP time 0.990
[#1] INFO:Minimization -- Session timer: Real time 0:00:03, CP time 3.840, 2 slices
a=-0.001237, [#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: deactivating const optimization
[#0] WARNING:NumericIntegration -- RooAdaptiveIntegratorND::dtor(model) WARNING: Number of suppressed warningings about integral evaluations where target precision was not reached is 18
[#1] INFO:Plotting -- RooAbsReal::plotOn(model) plot on x integrates over variables (z,y)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(model_Int[y,z]_Norm[x,y,z]) using numeric integrator RooAdaptiveIntegratorND to calculate Int(y,z)
- Date
- February 2018
- Authors
- Clemens Lange, Wouter Verkerke (C++ version)
Definition in file rf903_numintcache.py.


