doc/v630/rf315__projectpdf_8py.html

import ROOT


# Create pdf m(x,y) = gx(x|y) * g(y)

# --------------------------------------------------------------


# Increase default precision of numeric integration

# as self exercise has high sensitivity to numeric integration precision

ROOT.RooAbsPdf.defaultIntegratorConfig().setEpsRel(1e-8)

ROOT.RooAbsPdf.defaultIntegratorConfig().setEpsAbs(1e-8)


# Create observables

x = ROOT.RooRealVar("x", "x", -5, 5)

y = ROOT.RooRealVar("y", "y", -2, 2)


# Create function f(y) = a0 + a1*y

a0 = ROOT.RooRealVar("a0", "a0", 0)

a1 = ROOT.RooRealVar("a1", "a1", -1.5, -3, 1)

fy = ROOT.RooPolyVar("fy", "fy", y, [a0, a1])


# Create gaussx(x,f(y),sx)

sigmax = ROOT.RooRealVar("sigmax", "width of gaussian", 0.5)

gaussx = ROOT.RooGaussian("gaussx", "Gaussian in x with shifting mean in y", x, fy, sigmax)


# Create gaussy(y,0,2)

gaussy = ROOT.RooGaussian("gaussy", "Gaussian in y", y, 0.0, 2.0)


# Create gaussx(x,sx|y) * gaussy(y)

model = ROOT.RooProdPdf(

    "model",

    "gaussx(x|y)*gaussy(y)",

    {gaussy},

    Conditional=({gaussx}, {x}),

)


# Marginalize m(x,y) to m(x)

# ----------------------------------------------------


# modelx(x) = Int model(x,y) dy

modelx = model.createProjection({y})


# Use marginalized pdf as regular 1D pdf

# -----------------------------------------------


# Sample 1000 events from modelx

data = modelx.generateBinned({x}, 1000)


# Fit modelx to toy data

modelx.fitTo(data, Verbose=True, PrintLevel=-1)


# Plot modelx over data

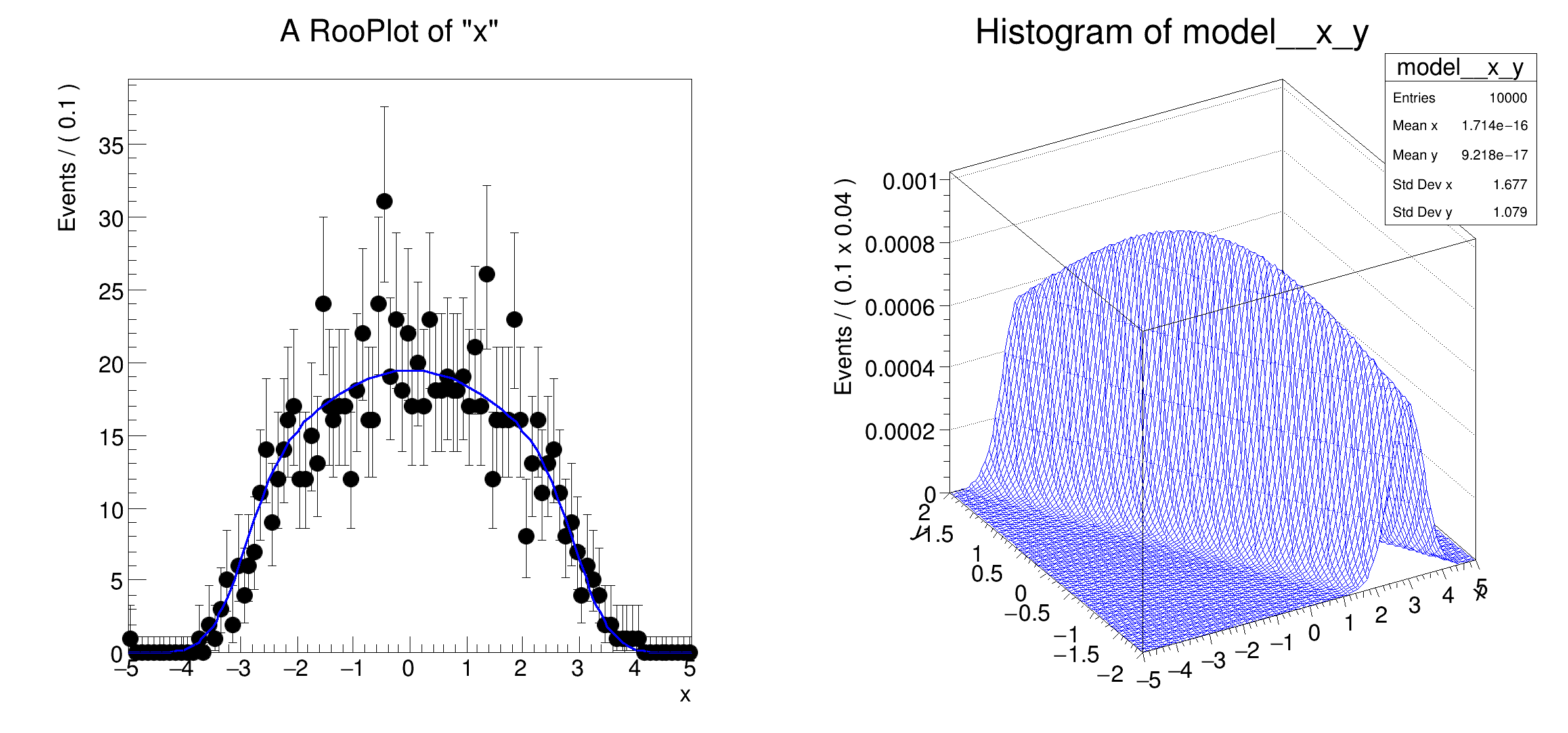
frame = x.frame(40)

data.plotOn(frame)

modelx.plotOn(frame)


# Make 2D histogram of model(x,y)

hh = model.createHistogram("x,y")

hh.SetLineColor(ROOT.kBlue)


c = ROOT.TCanvas("rf315_projectpdf", "rf315_projectpdf", 800, 400)

c.Divide(2)

c.cd(1)

ROOT.gPad.SetLeftMargin(0.15)

frame.GetYaxis().SetTitleOffset(1.4)

frame.Draw()

c.cd(2)

ROOT.gPad.SetLeftMargin(0.20)

hh.GetZaxis().SetTitleOffset(2.5)

hh.Draw("surf")

c.SaveAs("rf315_projectpdf.png")