

Basic functionality: interpreted functions and pdfs
import ROOT
x = ROOT.RooRealVar("x", "x", -20, 20)
alpha = ROOT.RooRealVar("alpha", "alpha", 5, 0.1, 10)
genpdf = ROOT.RooGenericPdf("genpdf", "genpdf", "(1+0.1*abs(x)+sin(sqrt(abs(x*alpha+0.1))))", [x, alpha])
data = genpdf.generate({x}, 10000)
genpdf.fitTo(data, PrintLevel=-1)
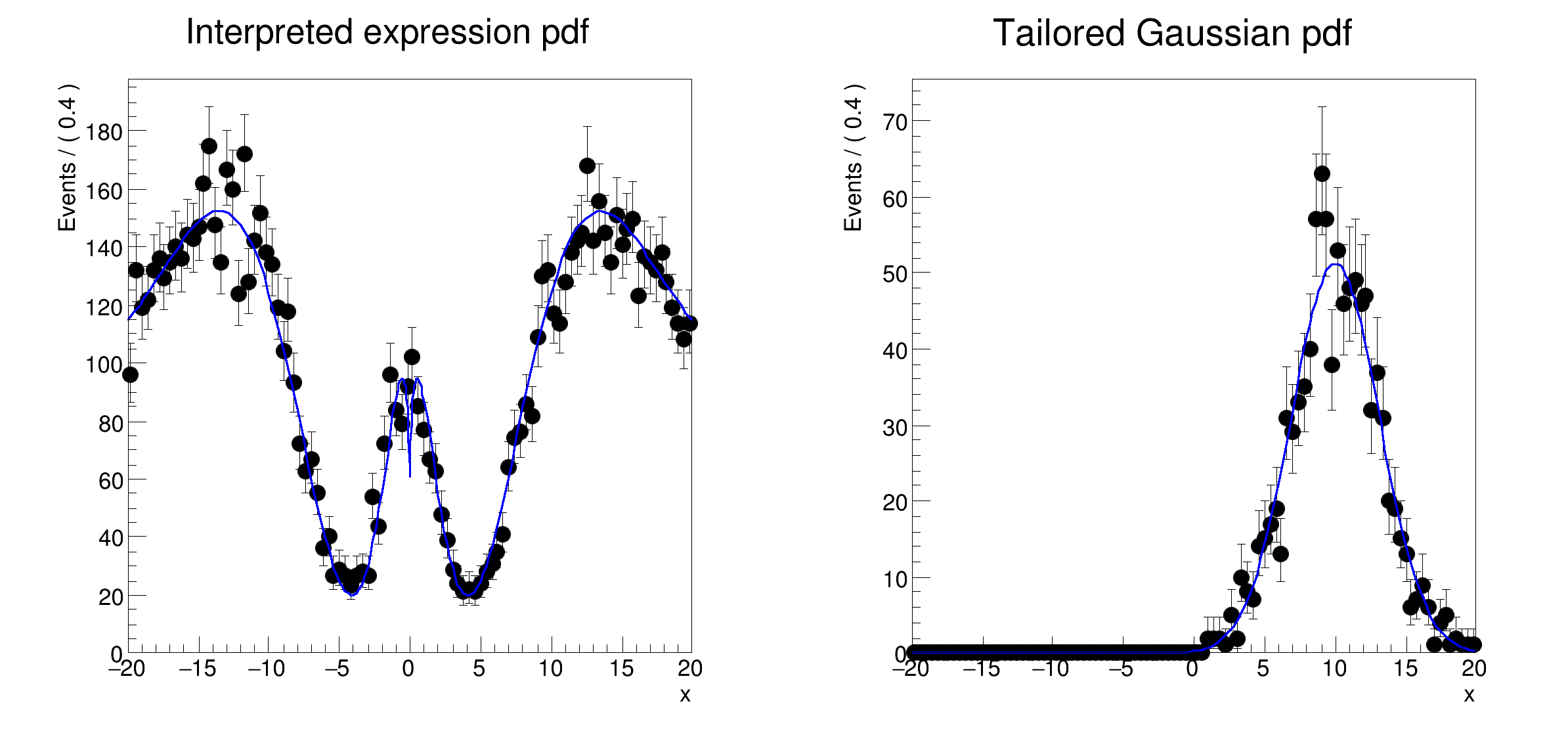
xframe = x.frame(Title="Interpreted expression pdf")
data.plotOn(xframe)
genpdf.plotOn(xframe)
mean2 = ROOT.RooRealVar("mean2", "mean^2", 10, 0, 200)
sigma = ROOT.RooRealVar("sigma", "sigma", 3, 0.1, 10)
mean = ROOT.RooFormulaVar("mean", "mean", "sqrt(mean2)", [mean2])
g2 = ROOT.RooGaussian("g2", "h2", x, mean, sigma)
g1 = ROOT.RooGaussian("g1", "g1", x, 10, 3)
data2 = g1.generate({x}, 1000)
r = g2.fitTo(data2, Save=True, PrintLevel=-1)
r.Print()
xframe2 = x.frame(Title="Tailored Gaussian pdf")
data2.plotOn(xframe2)
g2.plotOn(xframe2)
c = ROOT.TCanvas("rf103_interprfuncs", "rf103_interprfuncs", 800, 400)
c.Divide(2)
c.cd(1)
ROOT.gPad.SetLeftMargin(0.15)
xframe.GetYaxis().SetTitleOffset(1.4)
xframe.Draw()
c.cd(2)
ROOT.gPad.SetLeftMargin(0.15)
xframe2.GetYaxis().SetTitleOffset(1.4)
xframe2.Draw()
c.SaveAs("rf103_interprfuncs.png")
[#1] INFO:NumericIntegration -- RooRealIntegral::init(genpdf_Int[x]) using numeric integrator RooRombergIntegrator to calculate Int(x)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(genpdf_Int[x]) using numeric integrator RooRombergIntegrator to calculate Int(x)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(genpdf_Int[x]) using numeric integrator RooRombergIntegrator to calculate Int(x)
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: activating const optimization
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(genpdf_Int[x]) using numeric integrator RooRombergIntegrator to calculate Int(x)
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: activating const optimization
[#1] INFO:Minimization -- RooAbsMinimizerFcn::setOptimizeConst: deactivating const optimization
RooFitResult: minimized FCN value: 2551.39, estimated distance to minimum: 4.39288e-06
covariance matrix quality: Full, accurate covariance matrix
Status : MINIMIZE=0 HESSE=0
Floating Parameter FinalValue +/- Error
-------------------- --------------------------
mean2 1.0010e+02 +/- 1.98e+00
sigma 3.1172e+00 +/- 7.12e-02
- Date
- February 2018
- Authors
- Clemens Lange, Wouter Verkerke (C++ version)
Definition in file rf103_interprfuncs.py.


