doc/v628/rf703__effpdfprod_8py.html

import ROOT


# Define observables and decay pdf

# ---------------------------------------------------------------


# Declare observables

t = ROOT.RooRealVar("t", "t", 0, 5)


# Make pdf

tau = ROOT.RooRealVar("tau", "tau", -1.54, -4, -0.1)

model = ROOT.RooExponential("model", "model", t, tau)


# Define efficiency function

# ---------------------------------------------------


# Use error function to simulate turn-on slope

eff = ROOT.RooFormulaVar("eff", "0.5*(TMath::Erf((t-1)/0.5)+1)", [t])


# Define decay pdf with efficiency

# ---------------------------------------------------------------


# Multiply pdf(t) with efficiency in t

modelEff = ROOT.RooEffProd("modelEff", "model with efficiency", model, eff)


# Plot efficiency, pdf

# ----------------------------------------


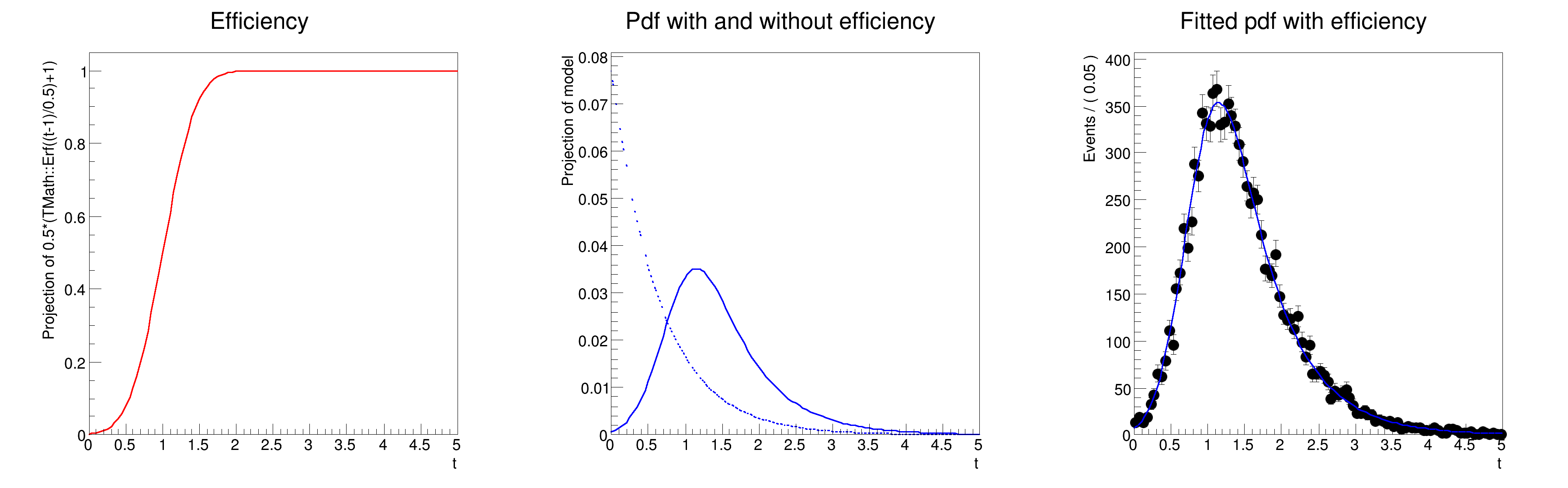
frame1 = t.frame(Title="Efficiency")

eff.plotOn(frame1, LineColor="r")


frame2 = t.frame(Title="Pdf with and without efficiency")


model.plotOn(frame2, LineStyle="--")

modelEff.plotOn(frame2)


# Generate toy data, fit model eff to data

# ------------------------------------------------------------------------------


# Generate events. If the input pdf has an internal generator, internal generator

# is used and an accept/reject sampling on the efficiency is applied.

data = modelEff.generate({t}, 10000)


# Fit pdf. The normalization integral is calculated numerically.

modelEff.fitTo(data, PrintLevel=-1)


# Plot generated data and overlay fitted pdf

frame3 = t.frame(Title="Fitted pdf with efficiency")

data.plotOn(frame3)

modelEff.plotOn(frame3)


c = ROOT.TCanvas("rf703_effpdfprod", "rf703_effpdfprod", 1200, 400)

c.Divide(3)

c.cd(1)

ROOT.gPad.SetLeftMargin(0.15)

frame1.GetYaxis().SetTitleOffset(1.4)

frame1.Draw()

c.cd(2)

ROOT.gPad.SetLeftMargin(0.15)

frame2.GetYaxis().SetTitleOffset(1.6)

frame2.Draw()

c.cd(3)

ROOT.gPad.SetLeftMargin(0.15)

frame3.GetYaxis().SetTitleOffset(1.6)

frame3.Draw()


c.SaveAs("rf703_effpdfprod.png")