doc/v628/rf313__paramranges_8C.html

#include "RooRealVar.h"

#include "RooDataSet.h"

#include "RooGaussian.h"

#include "RooConstVar.h"

#include "RooPolynomial.h"

#include "RooProdPdf.h"

#include "TCanvas.h"

#include "TAxis.h"

#include "RooPlot.h"

using namespace RooFit;


void rf313_paramranges()

{


   // C r e a t e   3 D   p d f

   // -------------------------


   // Define observable (x,y,z)

   RooRealVar x("x", "x", 0, 10);

   RooRealVar y("y", "y", 0, 10);

   RooRealVar z("z", "z", 0, 10);


   // Define 3 dimensional pdf

   RooRealVar z0("z0", "z0", -0.1, 1);

   RooPolynomial px("px", "px", x, RooConst(0));

   RooPolynomial py("py", "py", y, RooConst(0));

   RooPolynomial pz("pz", "pz", z, z0);

   RooProdPdf pxyz("pxyz", "pxyz", RooArgSet(px, py, pz));


   // D e f i n e d   n o n - r e c t a n g u l a r   r e g i o n   R   i n   ( x , y , z )

   // -------------------------------------------------------------------------------------


   //

   // R = Z[0 - 0.1*Y^2] * Y[0.1*X - 0.9*X] * X[0 - 10]

   //


   // Construct range parametrized in "R" in y [ 0.1*x, 0.9*x ]

   RooFormulaVar ylo("ylo", "0.1*x", x);

   RooFormulaVar yhi("yhi", "0.9*x", x);

   y.setRange("R", ylo, yhi);


   // Construct parametrized ranged "R" in z [ 0, 0.1*y^2 ]

   RooFormulaVar zlo("zlo", "0.0*y", y);

   RooFormulaVar zhi("zhi", "0.1*y*y", y);

   z.setRange("R", zlo, zhi);


   // C a l c u l a t e   i n t e g r a l   o f   n o r m a l i z e d   p d f   i n   R

   // ----------------------------------------------------------------------------------


   // Create integral over normalized pdf model over x,y,z in "R" region

   std::unique_ptr<RooAbsReal> intPdf{pxyz.createIntegral(RooArgSet(x, y, z), RooArgSet(x, y, z), "R")};


   // Plot value of integral as function of pdf parameter z0

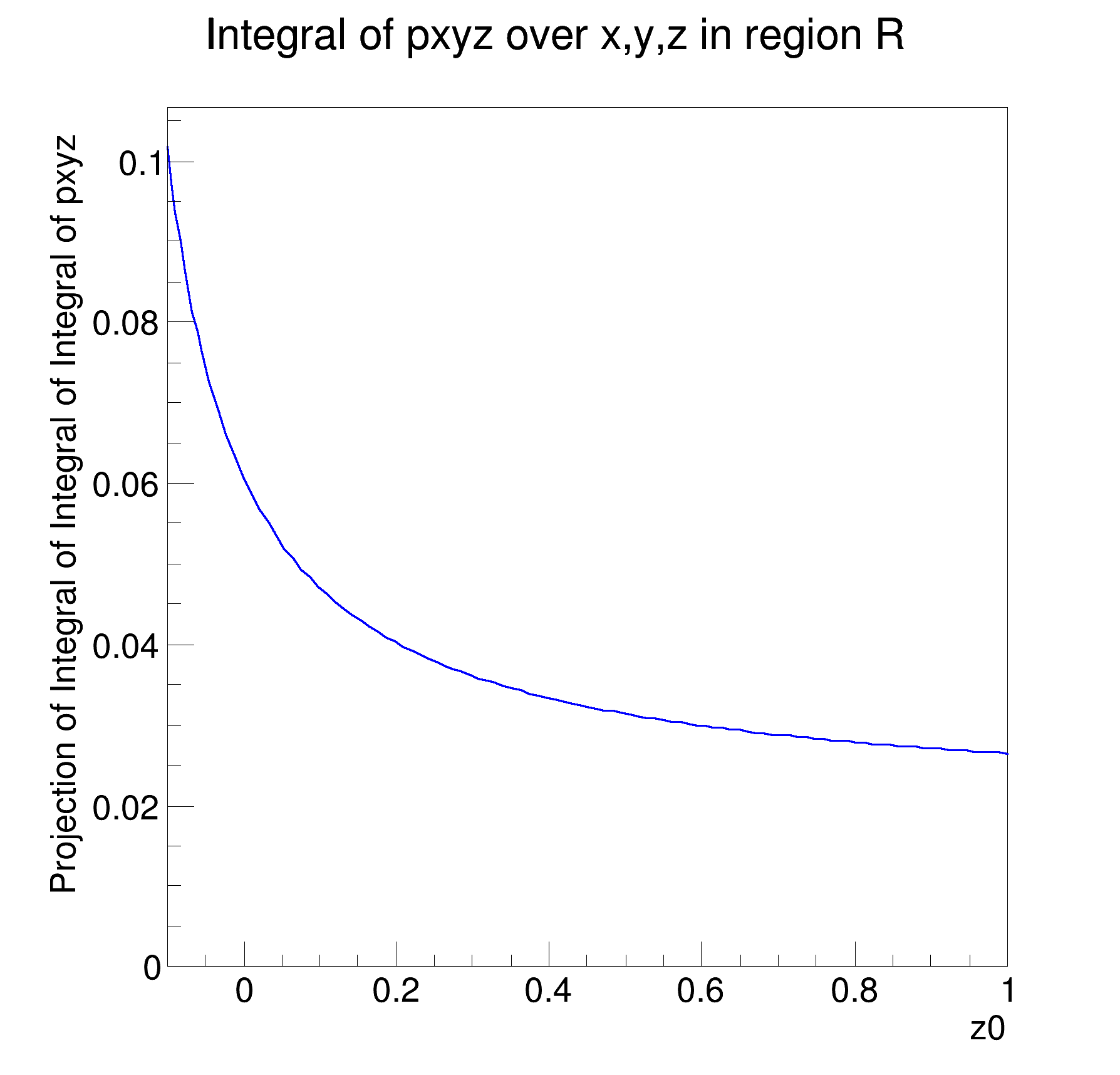
   RooPlot *frame = z0.frame(Title("Integral of pxyz over x,y,z in region R"));

   intPdf->plotOn(frame);


   new TCanvas("rf313_paramranges", "rf313_paramranges", 600, 600);

   gPad->SetLeftMargin(0.15);

   frame->GetYaxis()->SetTitleOffset(1.6);

   frame->Draw();


   return;

}

RooConstVar.h

RooDataSet.h

RooGaussian.h

RooPlot.h

RooPolynomial.h

RooProdPdf.h

RooRealVar.h

TAxis.h

TCanvas.h

gPad
#define gPad
Definition TVirtualPad.h:303

RooArgSet
RooArgSet is a container object that can hold multiple RooAbsArg objects.
Definition RooArgSet.h:55

RooFormulaVar
A RooFormulaVar is a generic implementation of a real-valued object, which takes a RooArgList of serv...
Definition RooFormulaVar.h:30

RooPlot
A RooPlot is a plot frame and a container for graphics objects within that frame.
Definition RooPlot.h:43

RooPlot::frame
static RooPlot * frame(const RooAbsRealLValue &var, double xmin, double xmax, Int_t nBins)
Create a new frame for a given variable in x.
Definition RooPlot.cxx:239

RooPlot::GetYaxis
TAxis * GetYaxis() const
Definition RooPlot.cxx:1276

RooPlot::Draw
void Draw(Option_t *options=nullptr) override
Draw this plot and all of the elements it contains.
Definition RooPlot.cxx:649

RooPolynomial
RooPolynomial implements a polynomial p.d.f of the form.
Definition RooPolynomial.h:25

RooProdPdf
RooProdPdf is an efficient implementation of a product of PDFs of the form.
Definition RooProdPdf.h:33

RooRealVar
RooRealVar represents a variable that can be changed from the outside.
Definition RooRealVar.h:40

TAttAxis::SetTitleOffset
virtual void SetTitleOffset(Float_t offset=1)
Set distance between the axis and the axis title.
Definition TAttAxis.cxx:298

TCanvas
The Canvas class.
Definition TCanvas.h:23

y
Double_t y[n]
Definition legend1.C:17

x
Double_t x[n]
Definition legend1.C:17

RooFit
The namespace RooFit contains mostly switches that change the behaviour of functions of PDFs (or othe...
Definition Common.h:18

rf313_paramranges
Definition rf313_paramranges.py:1