Zbi_Zgamma.py File Reference

Namespaces
namespace	Zbi_Zgamma

Detailed Description

Demonstrate Z_Bi = Z_Gamma

[#1] INFO:NumericIntegration -- RooRealIntegral::init([py_X_prior_b_X_px]_Norm[b]_denominator_Int[b]) using numeric integrator RooIntegrator1D to calculate Int(b)
[#1] INFO:NumericIntegration -- RooRealIntegral::init([py_X_prior_b]_Norm[b]_denominator_Int[b]) using numeric integrator RooIntegrator1D to calculate Int(b)
[#1] INFO:NumericIntegration -- RooRealIntegral::init([[py_X_prior_b]_Norm[b]_X_px_NORM[x]]_Int[b]) using numeric integrator RooIntegrator1D to calculate Int(b)
[#1] INFO:NumericIntegration -- RooRealIntegral::init([py_X_prior_b]_Norm[b]_denominator_Int[b]) using numeric integrator RooIntegrator1D to calculate Int(b)
[#1] INFO:NumericIntegration -- RooRealIntegral::init([py_X_prior_b]_Norm[b]_denominator_Int[b]) using numeric integrator RooIntegrator1D to calculate Int(b)
[#1] INFO:NumericIntegration -- RooRealIntegral::init([py_X_prior_b]_Norm[b]_denominator_Int[b]) using numeric integrator RooIntegrator1D to calculate Int(b)
[#1] INFO:NumericIntegration -- RooRealIntegral::init([[py_X_prior_b]_Norm[b]_X_px_cdf_NORM[x_prime]]_Int[b]) using numeric integrator RooIntegrator1D to calculate Int(b)
[#1] INFO:NumericIntegration -- RooRealIntegral::init([py_X_prior_b]_Norm[b]_denominator_Int[b]) using numeric integrator RooIntegrator1D to calculate Int(b)
[#1] INFO:NumericIntegration -- RooRealIntegral::init([[py_X_prior_b]_Norm[b]_X_px_cdf_Int[x_prime|CDF]_Norm[x_prime]]_Int[b|CDF]) using numeric integrator RooIntegrator1D to calculate Int(b)
[#1] INFO:NumericIntegration -- RooRealIntegral::init([py_X_prior_b]_Norm[b]_denominator_Int[b]) using numeric integrator RooIntegrator1D to calculate Int(b)
Hybrid p-value =  0.9992259057034769
Z_Gamma Significance  =  3.165495870670026
Z_Bi significance estimation:  3.1080438957471137

 
import ROOT
 
# Make model for prototype on/off problem
# Pois(x | s+b) * Pois(y | tau b )
# for Z_Gamma, use uniform prior on b.
w1 = ROOT.RooWorkspace("w")
w1.factory("Poisson::px(x[150,0,500],sum::splusb(s[0,0,100],b[100,0,300]))")
w1.factory("Poisson::py(y[100,0,500],prod::taub(tau[1.],b))")
w1.factory("Uniform::prior_b(b)")
 
# construct the Bayesian-averaged model (eg. a projection pdf)
# p'(x|s) = \int db p(x|s+b) * [ p(y|b) * prior(b) ]
w1.factory("PROJ::averagedModel(PROD::foo(px|b,py,prior_b),b)")
 
c = ROOT.TCanvas()
 
# plot it, blue is averaged model, red is b known exactly
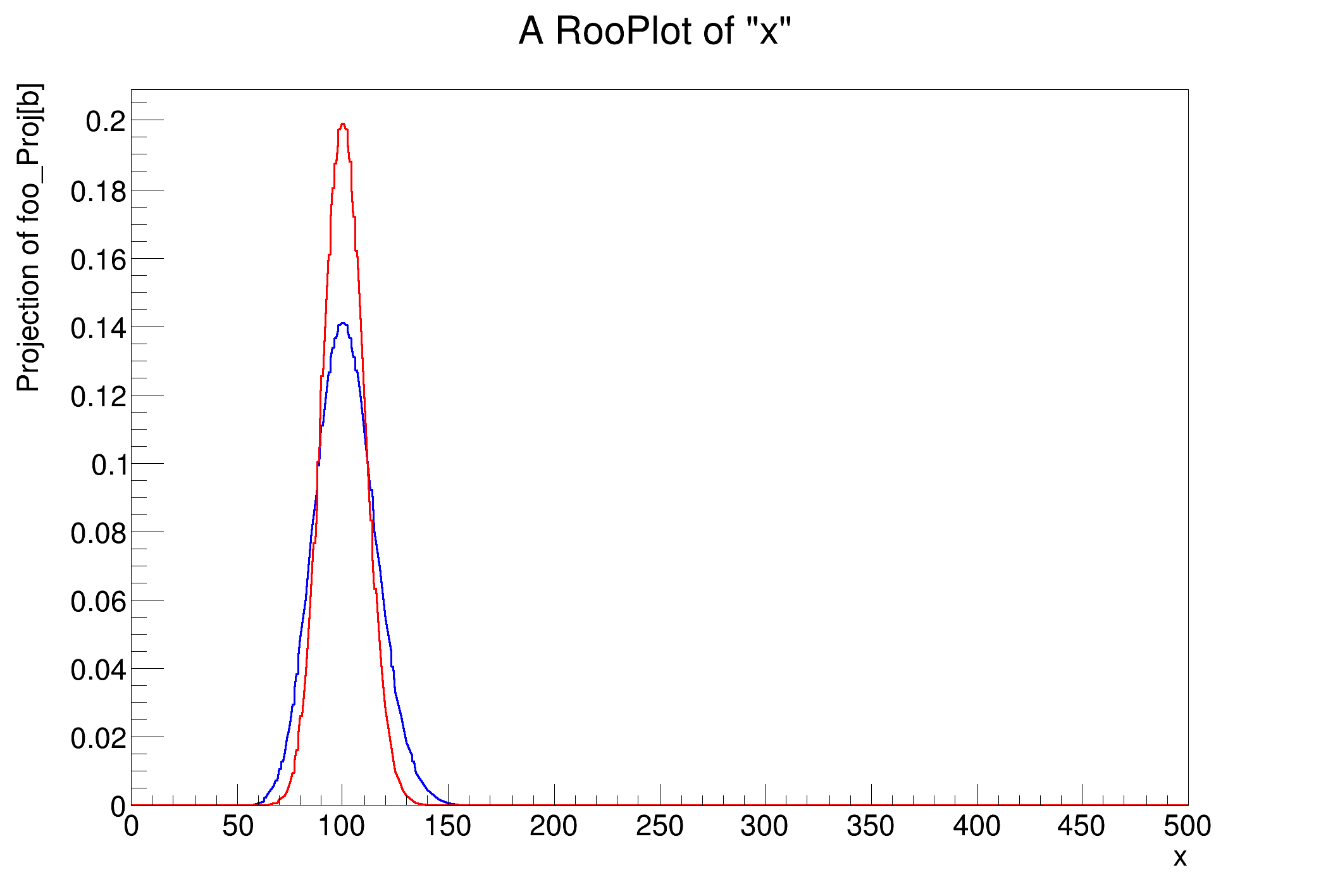
frame = w1["x"].frame()
w1["averagedModel"].plotOn(frame)
w1["px"].plotOn(frame, LineColor=ROOT.kRed)
frame.Draw()
 
# compare analytic calculation of Z_Bi
# with the numerical RooFit implementation of Z_Gamma
# for an example with x = 150, y = 100
 
# numeric RooFit Z_Gamma
w1["y"].setVal(100)
w1["x"].setVal(150)
cdf = w1["averagedModel"].createCdf(w1["x"])
cdf.getVal()  # get ugly print messages out of the way
 
print("Hybrid p-value = ", cdf.getVal())
print("Z_Gamma Significance  = ", ROOT.RooStats.PValueToSignificance(1 - cdf.getVal()))
 
# analytic Z_Bi
Z_Bi = ROOT.RooStats.NumberCountingUtils.BinomialWithTauObsZ(150, 100, 1)
print("Z_Bi significance estimation: ", Z_Bi)
 
c.SaveAs("Zbi_Zgamma.png")

Date

July 2022

Authors

Artem Busorgin, Kyle Cranmer and Wouter Verkerke (C++ version)

Definition in file Zbi_Zgamma.py.