df103_NanoAODHiggsAnalysis.C File Reference

Detailed Description

An example of complex analysis with RDataFrame: reconstructing the Higgs boson.

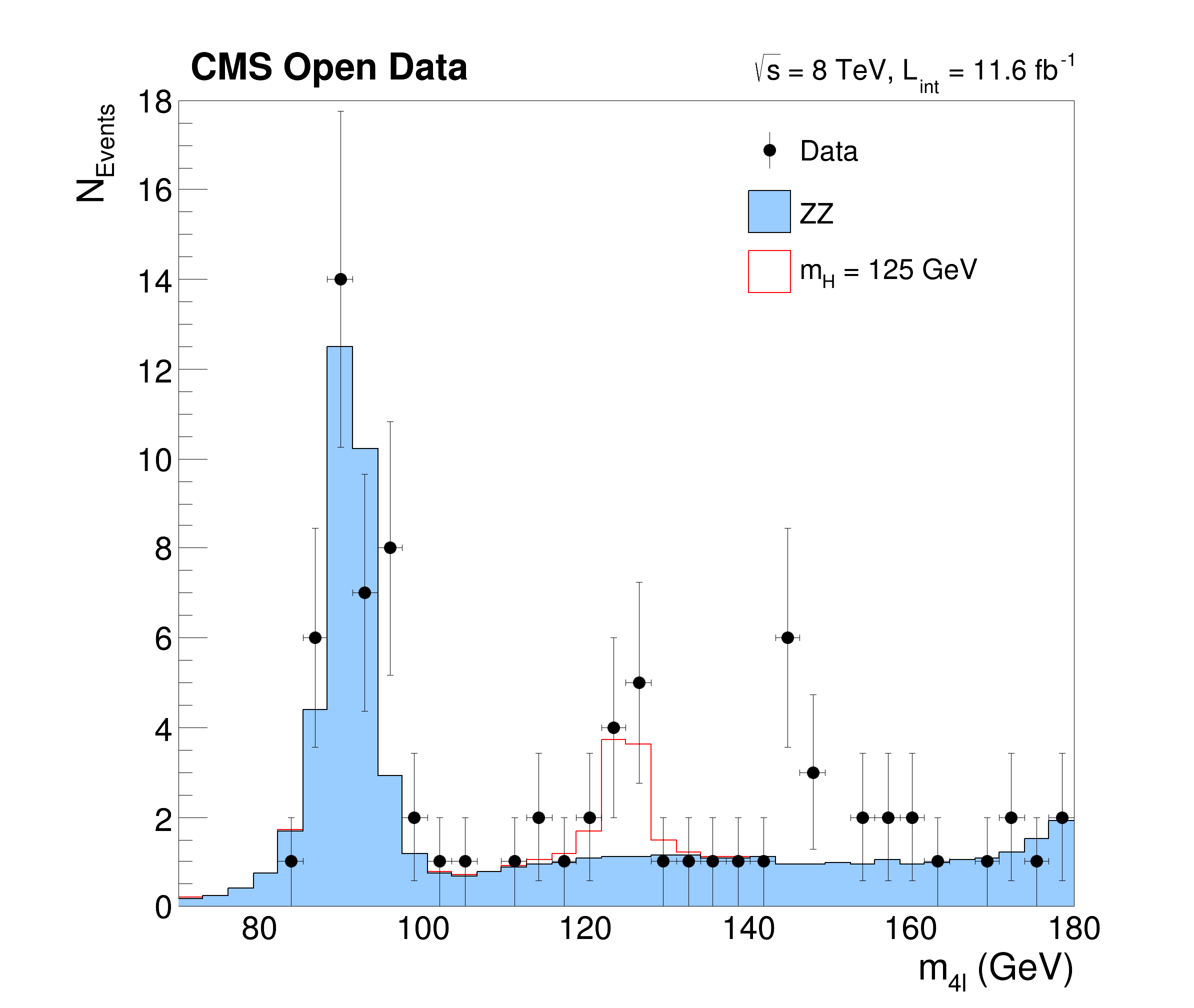
This tutorial is a simplified but yet complex example of an analysis reconstructing the Higgs boson decaying to two Z bosons from events with four leptons. The data and simulated events are taken from CERN OpenData representing a subset of the data recorded in 2012 with the CMS detector at the LHC. The tutorials follows the Higgs to four leptons analysis published on CERN Open Data portal (10.7483/OPENDATA.CMS.JKB8.RR42). The resulting plots show the invariant mass of the selected four lepton systems in different decay modes (four muons, four electrons and two of each kind) and in a combined plot indicating the decay of the Higgs boson with a mass of about 125 GeV.

The following steps are performed for each sample with data and simulated events in order to reconstruct the Higgs boson from the selected muons and electrons:

1. Select interesting events with multiple cuts on event properties, e.g., number of leptons, kinematics of the leptons and quality of the tracks.
2. Reconstruct two Z bosons of which only one on the mass shell from the selected events and apply additional cuts on the reconstructed objects.
3. Reconstruct the Higgs boson from the remaining Z boson candidates and calculate its invariant mass.

The tutorial has the fast mode enabled by default, which reads the data from already skimmed datasets with a total size of only 51MB. If the fast mode is disabled, the tutorial runs over the full dataset with a size of 12GB.

 
#include "ROOT/RDataFrame.hxx"
#include "ROOT/RVec.hxx"
#include "ROOT/RDF/RInterface.hxx"
#include "TCanvas.h"
#include "TH1D.h"
#include "TLatex.h"
#include "TLegend.h"
#include <Math/Vector4Dfwd.h>
#include <Math/GenVector/LorentzVector.h>
#include <Math/GenVector/PtEtaPhiM4D.h>
#include "TStyle.h"
#include <string>
 
using namespace ROOT::VecOps;
using RNode = ROOT::RDF::RNode;
using cRVecF = const ROOT::RVecF &;
 
const auto z_mass = 91.2;
 
// Select interesting events with four muons
RNode selection_4mu(RNode df)
{
   auto df_ge4m = df.Filter("nMuon>=4", "At least four muons");
   auto df_iso = df_ge4m.Filter("All(abs(Muon_pfRelIso04_all)<0.40)", "Require good isolation");
   auto df_kin = df_iso.Filter("All(Muon_pt>5) && All(abs(Muon_eta)<2.4)", "Good muon kinematics");
   auto df_ip3d = df_kin.Define("Muon_ip3d", "sqrt(Muon_dxy*Muon_dxy + Muon_dz*Muon_dz)");
   auto df_sip3d = df_ip3d.Define("Muon_sip3d", "Muon_ip3d/sqrt(Muon_dxyErr*Muon_dxyErr + Muon_dzErr*Muon_dzErr)");
   auto df_pv = df_sip3d.Filter("All(Muon_sip3d<4) && All(abs(Muon_dxy)<0.5) && All(abs(Muon_dz)<1.0)",
                                "Track close to primary vertex with small uncertainty");
   auto df_2p2n = df_pv.Filter("nMuon==4 && Sum(Muon_charge==1)==2 && Sum(Muon_charge==-1)==2",
                               "Two positive and two negative muons");
   return df_2p2n;
}
 
// Select interesting events with four electrons
RNode selection_4el(RNode df)
{
   auto df_ge4el = df.Filter("nElectron>=4", "At least our electrons");
   auto df_iso = df_ge4el.Filter("All(abs(Electron_pfRelIso03_all)<0.40)", "Require good isolation");
   auto df_kin = df_iso.Filter("All(Electron_pt>7) && All(abs(Electron_eta)<2.5)", "Good Electron kinematics");
   auto df_ip3d = df_kin.Define("Electron_ip3d", "sqrt(Electron_dxy*Electron_dxy + Electron_dz*Electron_dz)");
   auto df_sip3d = df_ip3d.Define("Electron_sip3d",
                                  "Electron_ip3d/sqrt(Electron_dxyErr*Electron_dxyErr + Electron_dzErr*Electron_dzErr)");
   auto df_pv = df_sip3d.Filter("All(Electron_sip3d<4) && All(abs(Electron_dxy)<0.5) && "
                                "All(abs(Electron_dz)<1.0)",
                                "Track close to primary vertex with small uncertainty");
   auto df_2p2n = df_pv.Filter("nElectron==4 && Sum(Electron_charge==1)==2 && Sum(Electron_charge==-1)==2",
                               "Two positive and two negative electrons");
   return df_2p2n;
}
 
// Select interesting events with two electrons and two muons
RNode selection_2el2mu(RNode df)
{
   auto df_ge2el2mu = df.Filter("nElectron>=2 && nMuon>=2", "At least two electrons and two muons");
   auto df_eta = df_ge2el2mu.Filter("All(abs(Electron_eta)<2.5) && All(abs(Muon_eta)<2.4)", "Eta cuts");
   auto pt_cuts = [](cRVecF mu_pt, cRVecF el_pt) {
      auto mu_pt_sorted = Reverse(Sort(mu_pt));
      if (mu_pt_sorted[0] > 20 && mu_pt_sorted[1] > 10) {
         return true;
      }
      auto el_pt_sorted = Reverse(Sort(el_pt));
      if (el_pt_sorted[0] > 20 && el_pt_sorted[1] > 10) {
         return true;
      }
      return false;
   };
   auto df_pt = df_eta.Filter(pt_cuts, {"Muon_pt", "Electron_pt"}, "Pt cuts");
   auto dr_cuts = [](cRVecF mu_eta, cRVecF mu_phi, cRVecF el_eta, cRVecF el_phi) {
      auto mu_dr = DeltaR(mu_eta[0], mu_eta[1], mu_phi[0], mu_phi[1]);
      auto el_dr = DeltaR(el_eta[0], el_eta[1], el_phi[0], el_phi[1]);
      if (mu_dr < 0.02 || el_dr < 0.02) {
         return false;
      }
      return true;
   };
   auto df_dr = df_pt.Filter(dr_cuts, {"Muon_eta", "Muon_phi", "Electron_eta", "Electron_phi"}, "Dr cuts");
   auto df_iso = df_dr.Filter("All(abs(Electron_pfRelIso03_all)<0.40) && All(abs(Muon_pfRelIso04_all)<0.40)",
                              "Require good isolation");
   auto df_el_ip3d = df_iso.Define("Electron_ip3d_el", "sqrt(Electron_dxy*Electron_dxy + Electron_dz*Electron_dz)");
   auto df_el_sip3d = df_el_ip3d.Define("Electron_sip3d_el",
                                        "Electron_ip3d_el/sqrt(Electron_dxyErr*Electron_dxyErr + "
                                        "Electron_dzErr*Electron_dzErr)");
   auto df_el_track = df_el_sip3d.Filter("All(Electron_sip3d_el<4) && All(abs(Electron_dxy)<0.5) && All(abs(Electron_dz)<1.0)",
                                         "Electron track close to primary vertex with small uncertainty");
   auto df_mu_ip3d = df_el_track.Define("Muon_ip3d_mu", "sqrt(Muon_dxy*Muon_dxy + Muon_dz*Muon_dz)");
   auto df_mu_sip3d = df_mu_ip3d.Define("Muon_sip3d_mu",
                                        "Muon_ip3d_mu/sqrt(Muon_dxyErr*Muon_dxyErr + Muon_dzErr*Muon_dzErr)");
   auto df_mu_track = df_mu_sip3d.Filter("All(Muon_sip3d_mu<4) && All(abs(Muon_dxy)<0.5) && All(abs(Muon_dz)<1.0)",
                                         "Muon track close to primary vertex with small uncertainty");
   auto df_2p2n = df_mu_track.Filter("Sum(Electron_charge)==0 && Sum(Muon_charge)==0",
                                     "Two opposite charged electron and muon pairs");
   return df_2p2n;
}
 
// Reconstruct two Z candidates from four leptons of the same kind
RVec<RVec<size_t>> reco_zz_to_4l(cRVecF pt, cRVecF eta, cRVecF phi, cRVecF mass, const ROOT::RVecI & charge)
{
   RVec<RVec<size_t>> idx(2);
   idx[0].reserve(2); idx[1].reserve(2);
 
   // Find first lepton pair with invariant mass closest to Z mass
   auto idx_cmb = Combinations(pt, 2);
   auto best_mass = -1;
   size_t best_i1 = 0; size_t best_i2 = 0;
   for (size_t i = 0; i < idx_cmb[0].size(); i++) {
      const auto i1 = idx_cmb[0][i];
      const auto i2 = idx_cmb[1][i];
      if (charge[i1] != charge[i2]) {
         ROOT::Math::PtEtaPhiMVector p1(pt[i1], eta[i1], phi[i1], mass[i1]);
         ROOT::Math::PtEtaPhiMVector p2(pt[i2], eta[i2], phi[i2], mass[i2]);
         const auto this_mass = (p1 + p2).M();
         if (std::abs(z_mass - this_mass) < std::abs(z_mass - best_mass)) {
            best_mass = this_mass;
            best_i1 = i1;
            best_i2 = i2;
         }
      }
   }
   idx[0].emplace_back(best_i1);
   idx[0].emplace_back(best_i2);
 
   // Reconstruct second Z from remaining lepton pair
   for (size_t i = 0; i < 4; i++) {
      if (i != best_i1 && i != best_i2) {
         idx[1].emplace_back(i);
      }
   }
 
   // Return indices of the pairs building two Z bosons
   return idx;
}
 
// Compute Z masses from four leptons of the same kind and sort ascending in distance to Z mass
ROOT::RVecF compute_z_masses_4l(const RVec<RVec<size_t>> &idx, cRVecF pt, cRVecF eta, cRVecF phi, cRVecF mass)
{
   ROOT::RVecF z_masses(2);
   for (size_t i = 0; i < 2; i++) {
      const auto i1 = idx[i][0]; const auto i2 = idx[i][1];
      ROOT::Math::PtEtaPhiMVector p1(pt[i1], eta[i1], phi[i1], mass[i1]);
      ROOT::Math::PtEtaPhiMVector p2(pt[i2], eta[i2], phi[i2], mass[i2]);
      z_masses[i] = (p1 + p2).M();
   }
   if (std::abs(z_masses[0] - z_mass) < std::abs(z_masses[1] - z_mass)) {
      return z_masses;
   } else {
      return Reverse(z_masses);
   }
}
 
// Compute mass of Higgs from four leptons of the same kind
float compute_higgs_mass_4l(const RVec<RVec<size_t>> &idx, cRVecF pt, cRVecF eta, cRVecF phi, cRVecF mass)
{
   const auto i1 = idx[0][0]; const auto i2 = idx[0][1];
   const auto i3 = idx[1][0]; const auto i4 = idx[1][1];
   ROOT::Math::PtEtaPhiMVector p1(pt[i1], eta[i1], phi[i1], mass[i1]);
   ROOT::Math::PtEtaPhiMVector p2(pt[i2], eta[i2], phi[i2], mass[i2]);
   ROOT::Math::PtEtaPhiMVector p3(pt[i3], eta[i3], phi[i3], mass[i3]);
   ROOT::Math::PtEtaPhiMVector p4(pt[i4], eta[i4], phi[i4], mass[i4]);
   return (p1 + p2 + p3 + p4).M();
}
 
// Apply selection on reconstructed Z candidates
RNode filter_z_candidates(RNode df)
{
   auto df_z1_cut = df.Filter("Z_mass[0] > 40 && Z_mass[0] < 120", "Mass of first Z candidate in [40, 120]");
   auto df_z2_cut = df_z1_cut.Filter("Z_mass[1] > 12 && Z_mass[1] < 120", "Mass of second Z candidate in [12, 120]");
   return df_z2_cut;
}
 
// Reconstruct Higgs from four muons
RNode reco_higgs_to_4mu(RNode df)
{
   // Filter interesting events
   auto df_base = selection_4mu(df);
 
   // Reconstruct Z systems
   auto df_z_idx =
      df_base.Define("Z_idx", reco_zz_to_4l, {"Muon_pt", "Muon_eta", "Muon_phi", "Muon_mass", "Muon_charge"});
 
   // Cut on distance between muons building Z systems
   auto filter_z_dr = [](const RVec<RVec<size_t>> &idx, cRVecF eta, cRVecF phi) {
      for (size_t i = 0; i < 2; i++) {
         const auto i1 = idx[i][0];
         const auto i2 = idx[i][1];
         const auto dr = DeltaR(eta[i1], eta[i2], phi[i1], phi[i2]);
         if (dr < 0.02) {
            return false;
         }
      }
      return true;
   };
   auto df_z_dr =
      df_z_idx.Filter(filter_z_dr, {"Z_idx", "Muon_eta", "Muon_phi"}, "Delta R separation of muons building Z system");
 
   // Compute masses of Z systems
   auto df_z_mass =
      df_z_dr.Define("Z_mass", compute_z_masses_4l, {"Z_idx", "Muon_pt", "Muon_eta", "Muon_phi", "Muon_mass"});
 
   // Cut on mass of Z candidates
   auto df_z_cut = filter_z_candidates(df_z_mass);
 
   // Reconstruct H mass
   auto df_h_mass =
      df_z_cut.Define("H_mass", compute_higgs_mass_4l, {"Z_idx", "Muon_pt", "Muon_eta", "Muon_phi", "Muon_mass"});
 
   return df_h_mass;
}
 
// Reconstruct Higgs from four electrons
RNode reco_higgs_to_4el(RNode df)
{
   // Filter interesting events
   auto df_base = selection_4el(df);
 
   // Reconstruct Z systems
   auto df_z_idx = df_base.Define("Z_idx", reco_zz_to_4l,
                                  {"Electron_pt", "Electron_eta", "Electron_phi", "Electron_mass", "Electron_charge"});
 
   // Cut on distance between Electrons building Z systems
   auto filter_z_dr = [](const RVec<RVec<size_t>> &idx, cRVecF eta, cRVecF phi) {
      for (size_t i = 0; i < 2; i++) {
         const auto i1 = idx[i][0];
         const auto i2 = idx[i][1];
         const auto dr = DeltaR(eta[i1], eta[i2], phi[i1], phi[i2]);
         if (dr < 0.02) {
            return false;
         }
      }
      return true;
   };
   auto df_z_dr = df_z_idx.Filter(filter_z_dr, {"Z_idx", "Electron_eta", "Electron_phi"},
                                  "Delta R separation of Electrons building Z system");
 
   // Compute masses of Z systems
   auto df_z_mass = df_z_dr.Define("Z_mass", compute_z_masses_4l,
                                   {"Z_idx", "Electron_pt", "Electron_eta", "Electron_phi", "Electron_mass"});
 
   // Cut on mass of Z candidates
   auto df_z_cut = filter_z_candidates(df_z_mass);
 
   // Reconstruct H mass
   auto df_h_mass = df_z_cut.Define("H_mass", compute_higgs_mass_4l,
                                    {"Z_idx", "Electron_pt", "Electron_eta", "Electron_phi", "Electron_mass"});
 
   return df_h_mass;
}
 
// Compute mass of two Z candidates from two electrons and two muons and sort ascending in distance to Z mass
ROOT::RVecF compute_z_masses_2el2mu(cRVecF el_pt, cRVecF el_eta, cRVecF el_phi, cRVecF el_mass, cRVecF mu_pt,
                                    cRVecF mu_eta, cRVecF mu_phi, cRVecF mu_mass)
{
   ROOT::Math::PtEtaPhiMVector p1(mu_pt[0], mu_eta[0], mu_phi[0], mu_mass[0]);
   ROOT::Math::PtEtaPhiMVector p2(mu_pt[1], mu_eta[1], mu_phi[1], mu_mass[1]);
   ROOT::Math::PtEtaPhiMVector p3(el_pt[0], el_eta[0], el_phi[0], el_mass[0]);
   ROOT::Math::PtEtaPhiMVector p4(el_pt[1], el_eta[1], el_phi[1], el_mass[1]);
   auto mu_z = (p1 + p2).M();
   auto el_z = (p3 + p4).M();
   ROOT::RVecF z_masses(2);
   if (std::abs(mu_z - z_mass) < std::abs(el_z - z_mass)) {
      z_masses[0] = mu_z;
      z_masses[1] = el_z;
   } else {
      z_masses[0] = el_z;
      z_masses[1] = mu_z;
   }
   return z_masses;
}
 
// Compute Higgs mass from two electrons and two muons
float compute_higgs_mass_2el2mu(cRVecF el_pt, cRVecF el_eta, cRVecF el_phi, cRVecF el_mass, cRVecF mu_pt, cRVecF mu_eta,
                                cRVecF mu_phi, cRVecF mu_mass)
{
   ROOT::Math::PtEtaPhiMVector p1(mu_pt[0], mu_eta[0], mu_phi[0], mu_mass[0]);
   ROOT::Math::PtEtaPhiMVector p2(mu_pt[1], mu_eta[1], mu_phi[1], mu_mass[1]);
   ROOT::Math::PtEtaPhiMVector p3(el_pt[0], el_eta[0], el_phi[0], el_mass[0]);
   ROOT::Math::PtEtaPhiMVector p4(el_pt[1], el_eta[1], el_phi[1], el_mass[1]);
   return (p1 + p2 + p3 + p4).M();
}
 
// Reconstruct Higgs from two electrons and two muons
RNode reco_higgs_to_2el2mu(RNode df)
{
   // Filter interesting events
   auto df_base = selection_2el2mu(df);
 
   // Compute masses of Z systems
   auto df_z_mass =
      df_base.Define("Z_mass", compute_z_masses_2el2mu, {"Electron_pt", "Electron_eta", "Electron_phi", "Electron_mass",
                                                       "Muon_pt", "Muon_eta", "Muon_phi", "Muon_mass"});
 
   // Cut on mass of Z candidates
   auto df_z_cut = filter_z_candidates(df_z_mass);
 
   // Reconstruct H mass
   auto df_h_mass = df_z_cut.Define(
      "H_mass", compute_higgs_mass_2el2mu,
      {"Electron_pt", "Electron_eta", "Electron_phi", "Electron_mass", "Muon_pt", "Muon_eta", "Muon_phi", "Muon_mass"});
 
   return df_h_mass;
}
 
// Plot invariant mass for signal and background processes from simulated events
// overlay the measured data.
template <typename T>
void plot(T sig, T bkg, T data, const std::string &x_label, const std::string &filename)
{
   // Canvas and general style options
   gStyle->SetOptStat(0);
   gStyle->SetTextFont(42);
   auto c = new TCanvas("c", "", 800, 700);
   c->SetLeftMargin(0.15);
 
   // Get signal and background histograms and stack them to show Higgs signal
   // on top of the background process
   auto h_sig = *sig;
   auto h_bkg = *bkg;
   auto h_cmb = *(TH1D*)(sig->Clone());
   h_cmb.Add(&h_bkg);
   h_cmb.SetTitle("");
   h_cmb.GetXaxis()->SetTitle(x_label.c_str());
   h_cmb.GetXaxis()->SetTitleSize(0.04);
   h_cmb.GetYaxis()->SetTitle("N_{Events}");
   h_cmb.GetYaxis()->SetTitleSize(0.04);
   h_cmb.SetLineColor(kRed);
   h_cmb.SetLineWidth(2);
   h_cmb.SetMaximum(18);
 
   h_bkg.SetLineWidth(2);
   h_bkg.SetFillStyle(1001);
   h_bkg.SetLineColor(kBlack);
   h_bkg.SetFillColor(kAzure - 9);
 
   // Get histogram of data points
   auto h_data = *data;
   h_data.SetLineWidth(1);
   h_data.SetMarkerStyle(20);
   h_data.SetMarkerSize(1.0);
   h_data.SetMarkerColor(kBlack);
   h_data.SetLineColor(kBlack);
 
   // Draw histograms
   h_cmb.DrawClone("HIST");
   h_bkg.DrawClone("HIST SAME");
   h_data.DrawClone("PE1 SAME");
 
   // Add legend
   TLegend legend(0.62, 0.70, 0.82, 0.88);
   legend.SetFillColor(0);
   legend.SetBorderSize(0);
   legend.SetTextSize(0.03);
   legend.AddEntry(&h_data, "Data", "PE1");
   legend.AddEntry(&h_bkg, "ZZ", "f");
   legend.AddEntry(&h_cmb, "m_{H} = 125 GeV", "f");
   legend.DrawClone();
 
   // Add header
   TLatex cms_label;
   cms_label.SetTextSize(0.04);
   cms_label.DrawLatexNDC(0.16, 0.92, "#bf{CMS Open Data}");
   TLatex header;
   header.SetTextSize(0.03);
   header.DrawLatexNDC(0.63, 0.92, "#sqrt{s} = 8 TeV, L_{int} = 11.6 fb^{-1}");
 
   // Save plot
   c->SaveAs(filename.c_str());
}
 
void df103_NanoAODHiggsAnalysis(const bool run_fast = true)
{
   // Enable multi-threading
   ROOT::EnableImplicitMT();
 
   // In fast mode, take samples from */cms_opendata_2012_nanoaod_skimmed/*, which has
   // the preselections from the selection_* functions already applied.
   std::string path = "root://eospublic.cern.ch//eos/root-eos/cms_opendata_2012_nanoaod/";
   if (run_fast) path = "root://eospublic.cern.ch//eos/root-eos/cms_opendata_2012_nanoaod_skimmed/";
 
   // Create dataframes for signal, background and data samples
 
   // Signal: Higgs -> 4 leptons
   ROOT::RDataFrame df_sig_4l("Events", path + "SMHiggsToZZTo4L.root");
 
   // Background: ZZ -> 4 leptons
   // Note that additional background processes from the original paper with minor contribution were left out for this
   // tutorial.
   ROOT::RDataFrame df_bkg_4mu("Events", path + "ZZTo4mu.root");
   ROOT::RDataFrame df_bkg_4el("Events", path + "ZZTo4e.root");
   ROOT::RDataFrame df_bkg_2el2mu("Events", path + "ZZTo2e2mu.root");
 
   // CMS data taken in 2012 (11.6 fb^-1 integrated luminosity)
   ROOT::RDataFrame df_data_doublemu(
      "Events", {path + "Run2012B_DoubleMuParked.root", path + "Run2012C_DoubleMuParked.root"});
   ROOT::RDataFrame df_data_doubleel(
      "Events", {path + "Run2012B_DoubleElectron.root", path + "Run2012C_DoubleElectron.root"});
 
   // Reconstruct Higgs to 4 muons
   auto df_sig_4mu_reco = reco_higgs_to_4mu(df_sig_4l);
   const auto luminosity = 11580.0;            // Integrated luminosity of the data samples
   const auto xsec_SMHiggsToZZTo4L = 0.0065;   // H->4l: Standard Model cross-section
   const auto nevt_SMHiggsToZZTo4L = 299973.0; // H->4l: Number of simulated events
   const auto nbins = 36;                      // Number of bins for the invariant mass spectrum
   auto df_h_sig_4mu = df_sig_4mu_reco
         .Define("weight", [&]() { return luminosity * xsec_SMHiggsToZZTo4L / nevt_SMHiggsToZZTo4L; }, {})
         .Histo1D({"h_sig_4mu", "", nbins, 70, 180}, "H_mass", "weight");
 
   const auto scale_ZZTo4l = 1.386;     // ZZ->4mu: Scale factor for ZZ to four leptons
   const auto xsec_ZZTo4mu = 0.077;     // ZZ->4mu: Standard Model cross-section
   const auto nevt_ZZTo4mu = 1499064.0; // ZZ->4mu: Number of simulated events
   auto df_bkg_4mu_reco = reco_higgs_to_4mu(df_bkg_4mu);
   auto df_h_bkg_4mu = df_bkg_4mu_reco
         .Define("weight", [&]() { return luminosity * xsec_ZZTo4mu * scale_ZZTo4l / nevt_ZZTo4mu; }, {})
         .Histo1D({"h_bkg_4mu", "", nbins, 70, 180}, "H_mass", "weight");
 
   auto df_data_4mu_reco = reco_higgs_to_4mu(df_data_doublemu);
   auto df_h_data_4mu = df_data_4mu_reco
         .Define("weight", []() { return 1.0; }, {})
         .Histo1D({"h_data_4mu", "", nbins, 70, 180}, "H_mass", "weight");
 
   // Reconstruct Higgs to 4 electrons
   auto df_sig_4el_reco = reco_higgs_to_4el(df_sig_4l);
   auto df_h_sig_4el = df_sig_4el_reco
         .Define("weight", [&]() { return luminosity * xsec_SMHiggsToZZTo4L / nevt_SMHiggsToZZTo4L; }, {})
         .Histo1D({"h_sig_4el", "", nbins, 70, 180}, "H_mass", "weight");
 
   const auto xsec_ZZTo4el = xsec_ZZTo4mu; // ZZ->4el: Standard Model cross-section
   const auto nevt_ZZTo4el = 1499093.0;    // ZZ->4el: Number of simulated events
   auto df_bkg_4el_reco = reco_higgs_to_4el(df_bkg_4el);
   auto df_h_bkg_4el = df_bkg_4el_reco
         .Define("weight", [&]() { return luminosity * xsec_ZZTo4el * scale_ZZTo4l / nevt_ZZTo4el; }, {})
         .Histo1D({"h_bkg_4el", "", nbins, 70, 180}, "H_mass", "weight");
 
   auto df_data_4el_reco = reco_higgs_to_4el(df_data_doubleel);
   auto df_h_data_4el = df_data_4el_reco.Define("weight", []() { return 1.0; }, {})
                           .Histo1D({"h_data_4el", "", nbins, 70, 180}, "H_mass", "weight");
 
   // Reconstruct Higgs to 2 electrons and 2 muons
   auto df_sig_2el2mu_reco = reco_higgs_to_2el2mu(df_sig_4l);
   auto df_h_sig_2el2mu = df_sig_2el2mu_reco
         .Define("weight", [&]() { return luminosity * xsec_SMHiggsToZZTo4L / nevt_SMHiggsToZZTo4L; }, {})
         .Histo1D({"h_sig_2el2mu", "", nbins, 70, 180}, "H_mass", "weight");
 
   const auto xsec_ZZTo2el2mu = 0.18;      // ZZ->2el2mu: Standard Model cross-section
   const auto nevt_ZZTo2el2mu = 1497445.0; // ZZ->2el2mu: Number of simulated events
   auto df_bkg_2el2mu_reco = reco_higgs_to_2el2mu(df_bkg_2el2mu);
   auto df_h_bkg_2el2mu = df_bkg_2el2mu_reco
         .Define("weight", [&]() { return luminosity * xsec_ZZTo2el2mu * scale_ZZTo4l / nevt_ZZTo2el2mu; }, {})
         .Histo1D({"h_bkg_2el2mu", "", nbins, 70, 180}, "H_mass", "weight");
 
   auto df_data_2el2mu_reco = reco_higgs_to_2el2mu(df_data_doublemu);
   auto df_h_data_2el2mu = df_data_2el2mu_reco.Define("weight", []() { return 1.0; }, {})
                              .Histo1D({"h_data_2el2mu_doublemu", "", nbins, 70, 180}, "H_mass", "weight");
 
   // RunGraphs allows to run the event loops of the separate RDataFrame graphs
   // concurrently. This results in an improved usage of the available resources
   // if each separate RDataFrame can not utilize all available resources, e.g.,
   // because not enough data is available.
   ROOT::RDF::RunGraphs({df_h_sig_4mu, df_h_bkg_4mu, df_h_data_4mu,
                         df_h_sig_4el, df_h_bkg_4el, df_h_data_4el,
                         df_h_sig_2el2mu, df_h_bkg_2el2mu, df_h_data_2el2mu});
 
   // Make plots
   plot(df_h_sig_4mu, df_h_bkg_4mu, df_h_data_4mu, "m_{4#mu} (GeV)", "higgs_4mu.pdf");
   plot(df_h_sig_4el, df_h_bkg_4el, df_h_data_4el, "m_{4e} (GeV)", "higgs_4el.pdf");
   plot(df_h_sig_2el2mu, df_h_bkg_2el2mu, df_h_data_2el2mu, "m_{2e2#mu} (GeV)", "higgs_2el2mu.pdf");
 
   // Combine channels for final plot
   auto h_data_4l = df_h_data_4mu.GetPtr();
   h_data_4l->Add(df_h_data_4el.GetPtr());
   h_data_4l->Add(df_h_data_2el2mu.GetPtr());
   auto h_sig_4l = df_h_sig_4mu.GetPtr();
   h_sig_4l->Add(df_h_sig_4el.GetPtr());
   h_sig_4l->Add(df_h_sig_2el2mu.GetPtr());
   auto h_bkg_4l = df_h_bkg_4mu.GetPtr();
   h_bkg_4l->Add(df_h_bkg_4el.GetPtr());
   h_bkg_4l->Add(df_h_bkg_2el2mu.GetPtr());
   plot(h_sig_4l, h_bkg_4l, h_data_4l, "m_{4l} (GeV)", "higgs_4l.pdf");
}
 
int main()
{
   df103_NanoAODHiggsAnalysis(/*fast=*/true);
}

Date

October 2018

Author

Stefan Wunsch (KIT, CERN)

Definition in file df103_NanoAODHiggsAnalysis.C.