df002_dataModel.C File Reference

Detailed Description

Show how to work with non-flat data models, e.g.

vectors of tracks.

This tutorial shows the possibility to use data models which are more complex than flat ntuples with RDataFrame

 
using FourVector = ROOT::Math::XYZTVector;
using FourVectorVec = std::vector<FourVector>;
using FourVectorRVec = ROOT::VecOps::RVec<FourVector>;
using CylFourVector = ROOT::Math::RhoEtaPhiVector;
 
// A simple helper function to fill a test tree: this makes the example
// stand-alone.
void fill_tree(const char *filename, const char *treeName)
{
   const double M = 0.13957; // set pi+ mass
   TRandom3 R(1);
 
   auto genTracks = [&](){
      FourVectorVec tracks;
      const auto nPart = R.Poisson(15);
      tracks.reserve(nPart);
      for (int j = 0; j < nPart; ++j) {
         const auto px = R.Gaus(0, 10);
         const auto py = R.Gaus(0, 10);
         const auto pt = sqrt(px * px + py * py);
         const auto eta = R.Uniform(-3, 3);
         const auto phi = R.Uniform(0.0, 2 * TMath::Pi());
         CylFourVector vcyl(pt, eta, phi);
         // set energy
         auto E = sqrt(vcyl.R() * vcyl.R() + M * M);
         // fill track vector
         tracks.emplace_back(vcyl.X(), vcyl.Y(), vcyl.Z(), E);
      }
      return tracks;
   };
 
   ROOT::RDataFrame d(64);
   d.Define("tracks", genTracks).Snapshot<FourVectorVec>(treeName, filename, {"tracks"});
}
 
int df002_dataModel()
{
 
   // We prepare an input tree to run on
   auto fileName = "df002_dataModel.root";
   auto treeName = "myTree";
   fill_tree(fileName, treeName);
 
   // We read the tree from the file and create a RDataFrame, a class that
   // allows us to interact with the data contained in the tree.
   ROOT::RDataFrame d(treeName, fileName, {"tracks"});
 
   // ## Operating on branches which are collection of objects
   // Here we deal with the simplest of the cuts: we decide to accept the event
   // only if the number of tracks is greater than 5.
   auto n_cut = [](const FourVectorRVec &tracks) { return tracks.size() > 8; };
   auto nentries = d.Filter(n_cut, {"tracks"}).Count();
 
   std::cout << *nentries << " passed all filters" << std::endl;
 
   // Another possibility consists in creating a new column containing the
   // quantity we are interested in.
   // In this example, we will cut on the number of tracks and plot their
   // transverse momentum.
   auto getPt = [](const FourVectorRVec &tracks) {
      return ROOT::VecOps::Map(tracks, [](const FourVector& v){return v.Pt();});
   };
 
   // We do the same for the weights.
   auto getPtWeights = [](const FourVectorRVec &tracks) {
      return ROOT::VecOps::Map(tracks, [](const FourVector& v){ return 1. / v.Pt();});
   };
 
   auto augmented_d = d.Define("tracks_n", [](const FourVectorRVec &tracks) { return (int)tracks.size(); })
                         .Filter([](int tracks_n) { return tracks_n > 2; }, {"tracks_n"})
                         .Define("tracks_pts", getPt)
                         .Define("tracks_pts_weights", getPtWeights);
 
   auto trN = augmented_d.Histo1D({"", "", 40, -.5, 39.5}, "tracks_n");
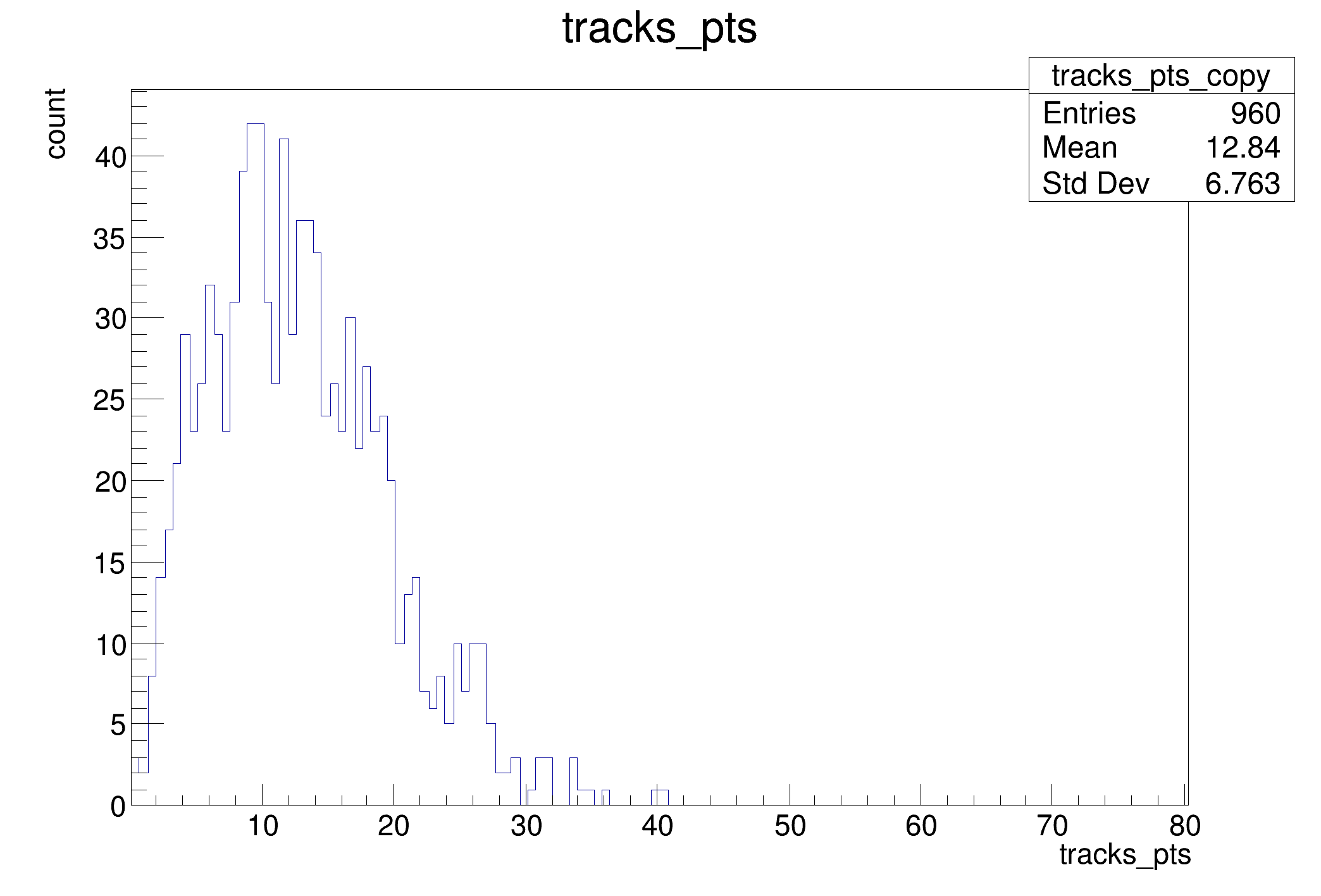
   auto trPts = augmented_d.Histo1D("tracks_pts");
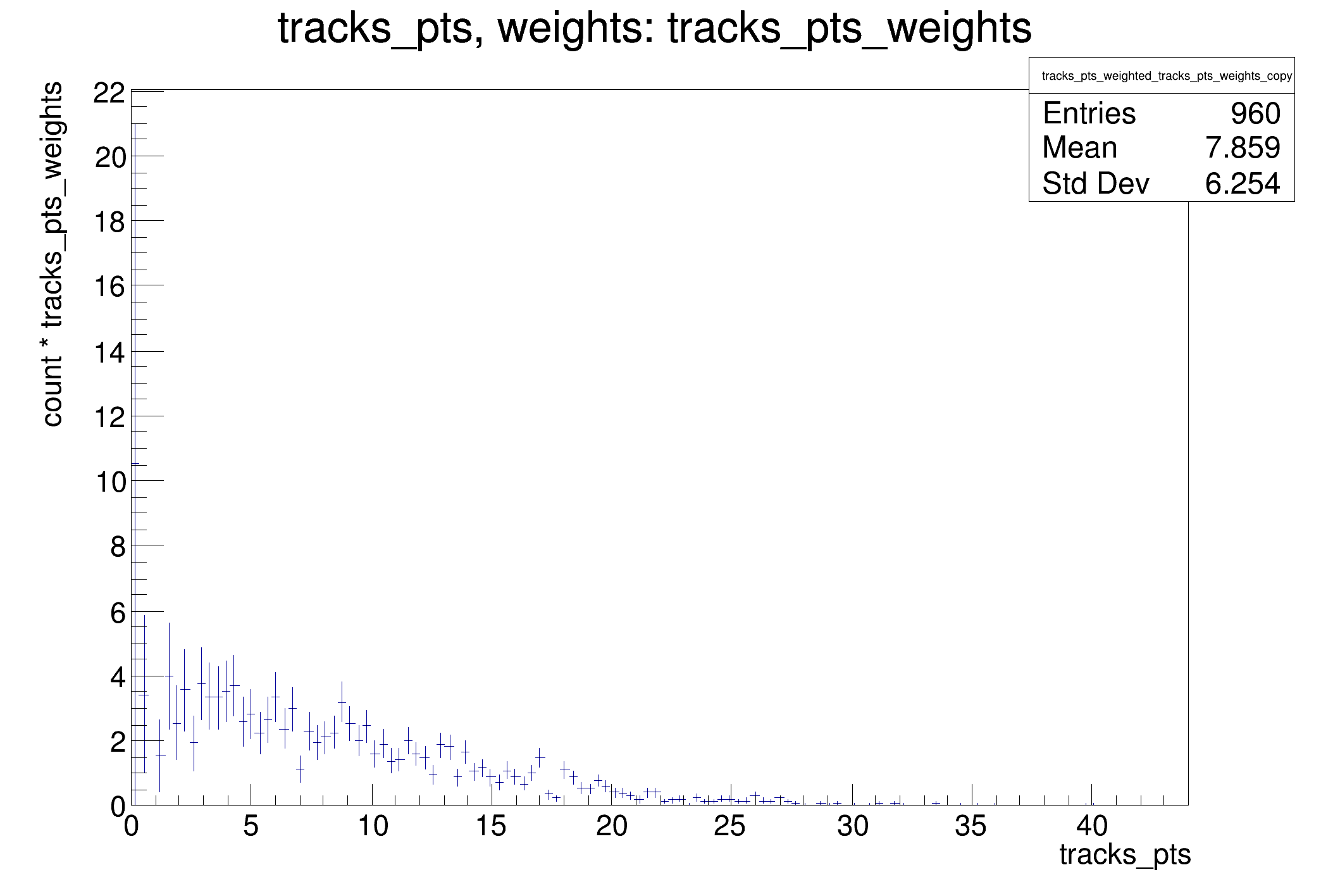
   auto trWPts = augmented_d.Histo1D("tracks_pts", "tracks_pts_weights");
 
   auto c1 = new TCanvas();
   trN->DrawCopy();
 
   auto c2 = new TCanvas();
   trPts->DrawCopy();
 
   auto c3 = new TCanvas();
   trWPts->DrawCopy();
 
   return 0;
}

Date

December 2016

Author

Danilo Piparo (CERN)

Definition in file df002_dataModel.C.