Advanced Spectra Processing.
This class contains advanced spectra processing functions for:
The algorithms in this class have been published in the following references:
These NIM papers are also available as doc or ps files from:
See also the online documentation and tutorials.
Definition at line 18 of file TSpectrum.h.
Public Types | |
| enum | { kBackOrder2 =0 , kBackOrder4 =1 , kBackOrder6 =2 , kBackOrder8 =3 , kBackIncreasingWindow =0 , kBackDecreasingWindow =1 , kBackSmoothing3 =3 , kBackSmoothing5 =5 , kBackSmoothing7 =7 , kBackSmoothing9 =9 , kBackSmoothing11 =11 , kBackSmoothing13 =13 , kBackSmoothing15 =15 } |
 Public Types inherited from TObject Public Types inherited from TObject | |
| enum | { kIsOnHeap = 0x01000000 , kNotDeleted = 0x02000000 , kZombie = 0x04000000 , kInconsistent = 0x08000000 , kBitMask = 0x00ffffff } |
| enum | { kSingleKey = BIT(0) , kOverwrite = BIT(1) , kWriteDelete = BIT(2) } |
| enum | EDeprecatedStatusBits { kObjInCanvas = BIT(3) } |
| enum | EStatusBits { kCanDelete = BIT(0) , kMustCleanup = BIT(3) , kIsReferenced = BIT(4) , kHasUUID = BIT(5) , kCannotPick = BIT(6) , kNoContextMenu = BIT(8) , kInvalidObject = BIT(13) } |
Public Member Functions | |
| TSpectrum () | |
| Constructor. | |
| TSpectrum (Int_t maxpositions, Double_t resolution=1) | |
| virtual | ~TSpectrum () |
| Destructor. | |
| virtual TH1 * | Background (const TH1 *hist, Int_t niter=20, Option_t *option="") |
| One-dimensional background estimation function. | |
| const char * | Background (Double_t *spectrum, Int_t ssize, Int_t numberIterations, Int_t direction, Int_t filterOrder, bool smoothing, Int_t smoothWindow, bool compton) |
| This function calculates background spectrum from source spectrum. | |
| const char * | Deconvolution (Double_t *source, const Double_t *response, Int_t ssize, Int_t numberIterations, Int_t numberRepetitions, Double_t boost) |
| One-dimensional deconvolution function. | |
| const char * | DeconvolutionRL (Double_t *source, const Double_t *response, Int_t ssize, Int_t numberIterations, Int_t numberRepetitions, Double_t boost) |
| One-dimensional deconvolution function. | |
| TH1 * | GetHistogram () const |
| Int_t | GetNPeaks () const |
| Double_t * | GetPositionX () const |
| Double_t * | GetPositionY () const |
| virtual void | Print (Option_t *option="") const |
| Print the array of positions. | |
| virtual Int_t | Search (const TH1 *hist, Double_t sigma=2, Option_t *option="", Double_t threshold=0.05) |
| One-dimensional peak search function. | |
| Int_t | Search1HighRes (Double_t *source, Double_t *destVector, Int_t ssize, Double_t sigma, Double_t threshold, bool backgroundRemove, Int_t deconIterations, bool markov, Int_t averWindow) |
| Old name of SearcHighRes introduced for back compatibility. | |
| Int_t | SearchHighRes (Double_t *source, Double_t *destVector, Int_t ssize, Double_t sigma, Double_t threshold, bool backgroundRemove, Int_t deconIterations, bool markov, Int_t averWindow) |
| One-dimensional high-resolution peak search function. | |
| void | SetResolution (Double_t resolution=1) |
| NOT USED resolution: determines resolution of the neighbouring peaks default value is 1 correspond to 3 sigma distance between peaks. | |
| const char * | SmoothMarkov (Double_t *source, Int_t ssize, Int_t averWindow) |
| One-dimensional markov spectrum smoothing function. | |
| const char * | Unfolding (Double_t *source, const Double_t **respMatrix, Int_t ssizex, Int_t ssizey, Int_t numberIterations, Int_t numberRepetitions, Double_t boost) |
| One-dimensional unfolding function. | |
 Public Member Functions inherited from TNamed Public Member Functions inherited from TNamed | |
| TNamed () | |
| TNamed (const char *name, const char *title) | |
| TNamed (const TNamed &named) | |
| TNamed copy ctor. | |
| TNamed (const TString &name, const TString &title) | |
| virtual | ~TNamed () |
| TNamed destructor. | |
| virtual void | Clear (Option_t *option="") |
| Set name and title to empty strings (""). | |
| virtual TObject * | Clone (const char *newname="") const |
| Make a clone of an object using the Streamer facility. | |
| virtual Int_t | Compare (const TObject *obj) const |
| Compare two TNamed objects. | |
| virtual void | Copy (TObject &named) const |
| Copy this to obj. | |
| virtual void | FillBuffer (char *&buffer) |
| Encode TNamed into output buffer. | |
| virtual const char * | GetName () const |
| Returns name of object. | |
| virtual const char * | GetTitle () const |
| Returns title of object. | |
| virtual ULong_t | Hash () const |
| Return hash value for this object. | |
| virtual Bool_t | IsSortable () const |
| virtual void | ls (Option_t *option="") const |
| List TNamed name and title. | |
| TNamed & | operator= (const TNamed &rhs) |
| TNamed assignment operator. | |
| virtual void | SetName (const char *name) |
| Set the name of the TNamed. | |
| virtual void | SetNameTitle (const char *name, const char *title) |
| Set all the TNamed parameters (name and title). | |
| virtual void | SetTitle (const char *title="") |
| Set the title of the TNamed. | |
| virtual Int_t | Sizeof () const |
| Return size of the TNamed part of the TObject. | |
 Public Member Functions inherited from TObject Public Member Functions inherited from TObject | |
| TObject () | |
| TObject constructor. | |
| TObject (const TObject &object) | |
| TObject copy ctor. | |
| virtual | ~TObject () |
| TObject destructor. | |
| void | AbstractMethod (const char *method) const |
| Use this method to implement an "abstract" method that you don't want to leave purely abstract. | |
| virtual void | AppendPad (Option_t *option="") |
| Append graphics object to current pad. | |
| virtual void | Browse (TBrowser *b) |
| Browse object. May be overridden for another default action. | |
| ULong_t | CheckedHash () |
| Check and record whether this class has a consistent Hash/RecursiveRemove setup (*) and then return the regular Hash value for this object. | |
| virtual const char * | ClassName () const |
| Returns name of class to which the object belongs. | |
| virtual void | Delete (Option_t *option="") |
| Delete this object. | |
| virtual Int_t | DistancetoPrimitive (Int_t px, Int_t py) |
| Computes distance from point (px,py) to the object. | |
| virtual void | Draw (Option_t *option="") |
| Default Draw method for all objects. | |
| virtual void | DrawClass () const |
| Draw class inheritance tree of the class to which this object belongs. | |
| virtual TObject * | DrawClone (Option_t *option="") const |
Draw a clone of this object in the current selected pad for instance with: gROOT->SetSelectedPad(gPad). | |
| virtual void | Dump () const |
| Dump contents of object on stdout. | |
| virtual void | Error (const char *method, const char *msgfmt,...) const |
| Issue error message. | |
| virtual void | Execute (const char *method, const char *params, Int_t *error=0) |
| Execute method on this object with the given parameter string, e.g. | |
| virtual void | Execute (TMethod *method, TObjArray *params, Int_t *error=0) |
| Execute method on this object with parameters stored in the TObjArray. | |
| virtual void | ExecuteEvent (Int_t event, Int_t px, Int_t py) |
| Execute action corresponding to an event at (px,py). | |
| virtual void | Fatal (const char *method, const char *msgfmt,...) const |
| Issue fatal error message. | |
| virtual TObject * | FindObject (const char *name) const |
| Must be redefined in derived classes. | |
| virtual TObject * | FindObject (const TObject *obj) const |
| Must be redefined in derived classes. | |
| virtual Option_t * | GetDrawOption () const |
| Get option used by the graphics system to draw this object. | |
| virtual const char * | GetIconName () const |
| Returns mime type name of object. | |
| virtual char * | GetObjectInfo (Int_t px, Int_t py) const |
| Returns string containing info about the object at position (px,py). | |
| virtual Option_t * | GetOption () const |
| virtual UInt_t | GetUniqueID () const |
| Return the unique object id. | |
| virtual Bool_t | HandleTimer (TTimer *timer) |
| Execute action in response of a timer timing out. | |
| Bool_t | HasInconsistentHash () const |
| Return true is the type of this object is known to have an inconsistent setup for Hash and RecursiveRemove (i.e. | |
| virtual void | Info (const char *method, const char *msgfmt,...) const |
| Issue info message. | |
| virtual Bool_t | InheritsFrom (const char *classname) const |
| Returns kTRUE if object inherits from class "classname". | |
| virtual Bool_t | InheritsFrom (const TClass *cl) const |
| Returns kTRUE if object inherits from TClass cl. | |
| virtual void | Inspect () const |
| Dump contents of this object in a graphics canvas. | |
| void | InvertBit (UInt_t f) |
| Bool_t | IsDestructed () const |
| IsDestructed. | |
| virtual Bool_t | IsEqual (const TObject *obj) const |
| Default equal comparison (objects are equal if they have the same address in memory). | |
| virtual Bool_t | IsFolder () const |
| Returns kTRUE in case object contains browsable objects (like containers or lists of other objects). | |
| R__ALWAYS_INLINE Bool_t | IsOnHeap () const |
| R__ALWAYS_INLINE Bool_t | IsZombie () const |
| void | MayNotUse (const char *method) const |
| Use this method to signal that a method (defined in a base class) may not be called in a derived class (in principle against good design since a child class should not provide less functionality than its parent, however, sometimes it is necessary). | |
| virtual Bool_t | Notify () |
| This method must be overridden to handle object notification. | |
| void | Obsolete (const char *method, const char *asOfVers, const char *removedFromVers) const |
| Use this method to declare a method obsolete. | |
| void | operator delete (void *ptr) |
| Operator delete. | |
| void | operator delete[] (void *ptr) |
| Operator delete []. | |
| void * | operator new (size_t sz) |
| void * | operator new (size_t sz, void *vp) |
| void * | operator new[] (size_t sz) |
| void * | operator new[] (size_t sz, void *vp) |
| TObject & | operator= (const TObject &rhs) |
| TObject assignment operator. | |
| virtual void | Paint (Option_t *option="") |
| This method must be overridden if a class wants to paint itself. | |
| virtual void | Pop () |
| Pop on object drawn in a pad to the top of the display list. | |
| virtual Int_t | Read (const char *name) |
| Read contents of object with specified name from the current directory. | |
| virtual void | RecursiveRemove (TObject *obj) |
| Recursively remove this object from a list. | |
| void | ResetBit (UInt_t f) |
| virtual void | SaveAs (const char *filename="", Option_t *option="") const |
| Save this object in the file specified by filename. | |
| virtual void | SavePrimitive (std::ostream &out, Option_t *option="") |
| Save a primitive as a C++ statement(s) on output stream "out". | |
| void | SetBit (UInt_t f) |
| void | SetBit (UInt_t f, Bool_t set) |
| Set or unset the user status bits as specified in f. | |
| virtual void | SetDrawOption (Option_t *option="") |
| Set drawing option for object. | |
| virtual void | SetUniqueID (UInt_t uid) |
| Set the unique object id. | |
| virtual void | SysError (const char *method, const char *msgfmt,...) const |
| Issue system error message. | |
| R__ALWAYS_INLINE Bool_t | TestBit (UInt_t f) const |
| Int_t | TestBits (UInt_t f) const |
| virtual void | UseCurrentStyle () |
| Set current style settings in this object This function is called when either TCanvas::UseCurrentStyle or TROOT::ForceStyle have been invoked. | |
| virtual void | Warning (const char *method, const char *msgfmt,...) const |
| Issue warning message. | |
| virtual Int_t | Write (const char *name=0, Int_t option=0, Int_t bufsize=0) |
| Write this object to the current directory. | |
| virtual Int_t | Write (const char *name=0, Int_t option=0, Int_t bufsize=0) const |
| Write this object to the current directory. | |
Static Public Member Functions | |
| static void | SetAverageWindow (Int_t w=3) |
| Static function: Set average window of searched peaks (see TSpectrum::SearchHighRes). | |
| static void | SetDeconIterations (Int_t n=3) |
| Static function: Set max number of decon iterations in deconvolution operation (see TSpectrum::SearchHighRes). | |
| static TH1 * | StaticBackground (const TH1 *hist, Int_t niter=20, Option_t *option="") |
| Static function, interface to TSpectrum::Background. | |
| static Int_t | StaticSearch (const TH1 *hist, Double_t sigma=2, Option_t *option="goff", Double_t threshold=0.05) |
| Static function, interface to TSpectrum::Search. | |
 Static Public Member Functions inherited from TObject Static Public Member Functions inherited from TObject | |
| static Longptr_t | GetDtorOnly () |
| Return destructor only flag. | |
| static Bool_t | GetObjectStat () |
| Get status of object stat flag. | |
| static void | SetDtorOnly (void *obj) |
| Set destructor only flag. | |
| static void | SetObjectStat (Bool_t stat) |
| Turn on/off tracking of objects in the TObjectTable. | |
Protected Attributes | |
| TH1 * | fHistogram |
| resulting histogram | |
| Int_t | fMaxPeaks |
| Maximum number of peaks to be found. | |
| Int_t | fNPeaks |
| number of peaks found | |
| Double_t * | fPosition |
| [fNPeaks] array of current peak positions | |
| Double_t * | fPositionX |
| [fNPeaks] X position of peaks | |
| Double_t * | fPositionY |
| [fNPeaks] Y position of peaks | |
| Double_t | fResolution |
| NOT USED resolution of the neighboring peaks | |
 Protected Attributes inherited from TNamed Protected Attributes inherited from TNamed | |
| TString | fName |
| TString | fTitle |
Static Protected Attributes | |
| static Int_t | fgAverageWindow = 3 |
| Average window of searched peaks. | |
| static Int_t | fgIterations = 3 |
| Maximum number of decon iterations (default=3) | |
Private Member Functions | |
| TSpectrum (const TSpectrum &) | |
| TSpectrum & | operator= (const TSpectrum &) |
Additional Inherited Members | |
 Protected Types inherited from TObject Protected Types inherited from TObject | |
| enum | { kOnlyPrepStep = BIT(3) } |
 Protected Member Functions inherited from TObject Protected Member Functions inherited from TObject | |
| virtual void | DoError (int level, const char *location, const char *fmt, va_list va) const |
| Interface to ErrorHandler (protected). | |
| void | MakeZombie () |
#include <TSpectrum.h>
| anonymous enum |
Definition at line 36 of file TSpectrum.h.
|
private |
| TSpectrum::TSpectrum | ( | ) |
Constructor.
Definition at line 53 of file TSpectrum.cxx.
Definition at line 73 of file TSpectrum.cxx.
|
virtual |
Destructor.
Definition at line 90 of file TSpectrum.cxx.
One-dimensional background estimation function.
This function calculates the background spectrum in the input histogram h. The background is returned as a histogram.
NOTE that the background is only evaluated in the current range of h. ie, if h has a bin range (set via h->GetXaxis()->SetRange(binmin,binmax), the returned histogram will be created with the same number of bins as the input histogram h, but only bins from binmin to binmax will be filled with the estimated background.
Definition at line 155 of file TSpectrum.cxx.
| const char * TSpectrum::Background | ( | Double_t * | spectrum, |
| Int_t | ssize, | ||
| Int_t | numberIterations, | ||
| Int_t | direction, | ||
| Int_t | filterOrder, | ||
| bool | smoothing, | ||
| Int_t | smoothWindow, | ||
| bool | compton | ||
| ) |
This function calculates background spectrum from source spectrum.
The result is placed in the vector pointed by spe1945ctrum pointer. The goal is to separate the useful information (peaks) from useless information (background).
\[ v_p(i) = min \left\{ v_{p-1}(i)^{\frac{\left[v_{p-1}(i+p)+v_{p-1}(i-p)\right]}{2}} \right\} \]
where p = 1, 2, ..., numberIterations. In fact it represents second order difference filter (-1,2,-1).
One can also change the direction of the change of the clipping window, the order of the clipping filter, to include smoothing, to set width of smoothing window and to include the estimation of Compton edges. On successful completion it returns 0. On error it returns pointer to the string describing error.
Example of the estimation of background for number of iterations=6. Original spectrum is shown in black color, estimated background in red color.

In Example 1. one can notice that at the edges of the peaks the estimated background goes under the peaks. An alternative approach is to decrease the clipping window from a given value numberIterations to the value of one, which is presented in this example.
Example of the estimation of background for numberIterations=6 using decreasing clipping window algorithm. Original spectrum is shown in black color, estimated background in red color.

The question is how to choose the width of the clipping window, i.e., numberIterations parameter. The influence of this parameter on the estimated background is illustrated in Example 3.
Example of the influence of clipping window width on the estimated background for numberIterations=4 (red line), 6 (orange line) 8 (green line) using decreasing clipping window algorithm.
in general one should set this parameter so that the value 2*numberIterations+1 was greater than the widths of preserved objects (peaks).

another example for very complex spectrum is given here.
Example of the influence of clipping window width on the estimated background for numberIterations=10 (red line), 20 (blue line), 30 (green line) and 40 (magenta line) using decreasing clipping window algorithm.

Second order difference filter removes linear (quasi-linear) background and preserves symmetrical peaks. However if the shape of the background is more complex one can employ higher-order clipping filters.
Example of the influence of clipping filter difference order on the estimated background for fNnumberIterations=40, 2-nd order red line, 4-th order blue line, 6-th order green line and 8-th order magenta line, and using decreasing clipping window algorithm.

The estimate of the background can be influenced by noise present in the spectrum. We proposed the algorithm of the background estimate with simultaneous smoothing. In the original algorithm without smoothing, the estimated background snatches the lower spikes in the noise. Consequently, the areas of peaks are biased by this error.


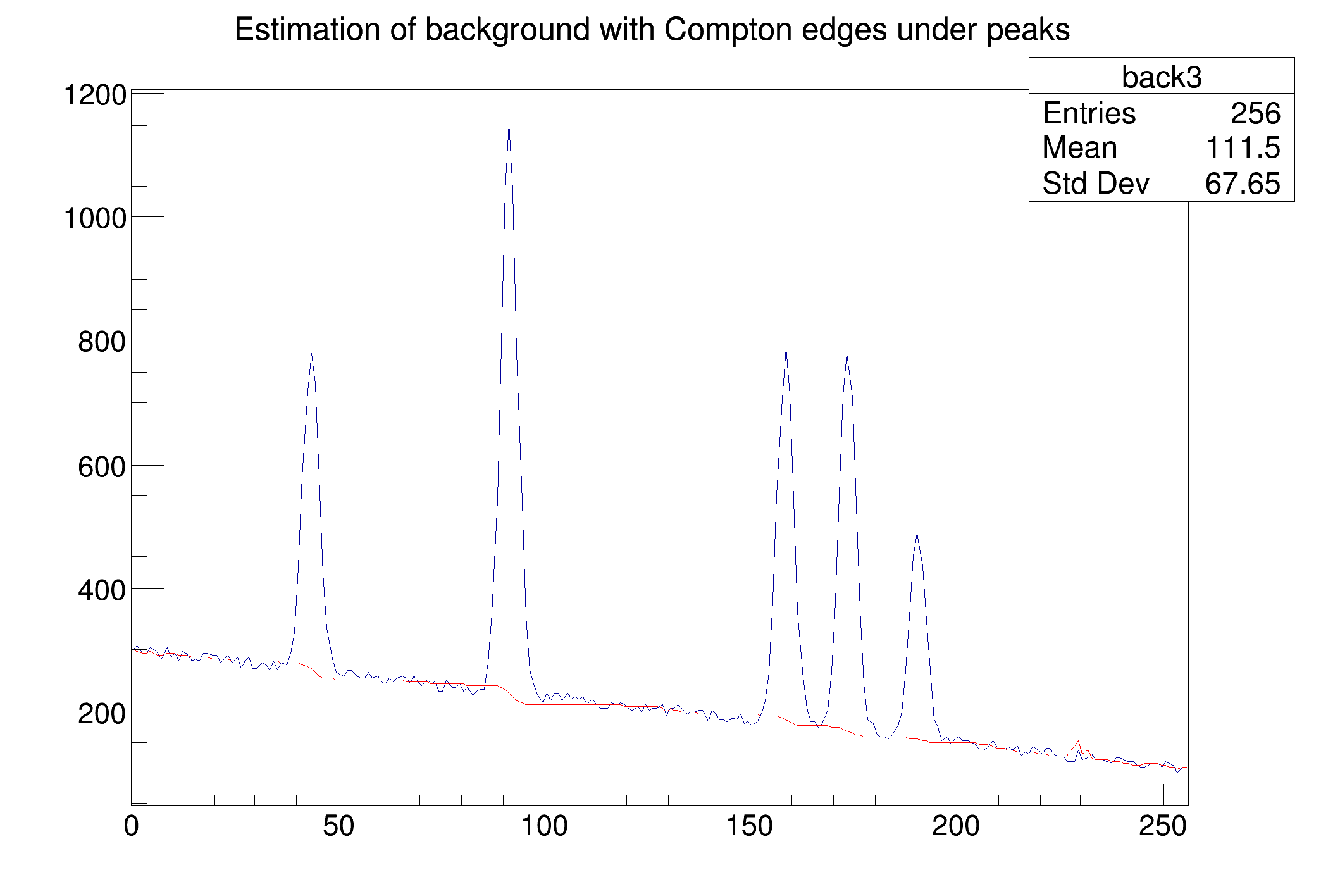
Sometimes it is necessary to include also the Compton edges into the estimate of the background. This example presents the synthetic spectrum with Compton edges. The background was estimated using the 8-th order filter with the estimation of the Compton edges using decreasing clipping window algorithm (numberIterations=10) with smoothing (smoothingWindow=5).
Example of the estimate of the background with Compton edges (red line) for numberIterations=10, 8-th order difference filter, using decreasing clipping window algorithm and smoothing (smoothingWindow=5).
Definition at line 515 of file TSpectrum.cxx.
| const char * TSpectrum::Deconvolution | ( | Double_t * | source, |
| const Double_t * | response, | ||
| Int_t | ssize, | ||
| Int_t | numberIterations, | ||
| Int_t | numberRepetitions, | ||
| Double_t | boost | ||
| ) |
One-dimensional deconvolution function.
This function calculates deconvolution from source spectrum according to response spectrum using Gold deconvolution algorithm. The result is placed in the vector pointed by source pointer. On successful completion it returns 0. On error it returns pointer to the string describing error. If desired after every numberIterations one can apply boosting operation (exponential function with exponent given by boost coefficient) and repeat it numberRepetitions times.
The goal of this function is the improvement of the resolution in spectra, decomposition of multiplets. The mathematical formulation of the convolution system is:
\[ y(i) = \sum_{k=0}^{N-1} h(i-k)x(k), i=0,1,2,...,N-1 \]
where h(i) is the impulse response function, x, y are input and output vectors, respectively, N is the length of x and h vectors. In matrix form we have:
\[ \begin{bmatrix} y(0) \\ y(1) \\ \dots \\ y(2N-2) \\ y(2N-1) \end{bmatrix} = \begin{bmatrix} h(0) & 0 & 0 & \dots & 0 \\ h(1) & h(0) & 0 & \dots & \dots \\ \dots & h(1) & h(0) & \dots & \dots \\ \dots & \dots & h(1) & \dots & \dots \\ \dots & \dots & \dots & \dots & \dots \\ h(N-1) & \dots & \dots &\dots & 0 \\ 0 & h(N-1) & \dots & \dots & h(0) \\ 0 & 0 & h(N-1) & \dots & h(1) \\ \dots & \dots & \dots & \dots & \dots \\ 0 & 0 & 0 & \dots & h(N-1) \end{bmatrix} \begin{bmatrix} x(0) \\ x(1) \\ \dots \\ x(N-1) \end{bmatrix} \]
Let us assume that we know the response and the output vector (spectrum) of the above given system. The deconvolution represents solution of the overdetermined system of linear equations, i.e., the calculation of the vector x. From numerical stability point of view the operation of deconvolution is extremely critical (ill-posed problem) as well as time consuming operation. The Gold deconvolution algorithm proves to work very well, other methods (Fourier, VanCittert etc) oscillate. It is suitable to process positive definite data (e.g. histograms).
\[ y = Hx \\ H^{T}y = H^{T}Hx \\ y^{'} = H^{'}x \\ x_{i}^{(k+1)} = \frac{y_{i}^{'}}{\sum_{m=0}^{N-1}H_{im}^{'}x_{m}{(k)}}x_{i}{(k)}, i=0,1,2,...,N-1 \\ k = 1,2,3,...,L x^{0} = [1,1, ..., 1]^T \]
Where L is given number of iterations (numberIterations parameter).
response function (usually peak) should be shifted left to the first non-zero channel (bin).


First let us study the influence of the number of iterations on the deconvolved spectrum (Fig. 12).

For relatively narrow peaks in the above given example the Gold deconvolution method is able to decompose overlapping peaks practically to delta - functions. In the next example we have chosen a synthetic data (spectrum, 256 channels) consisting of 5 very closely positioned, relatively wide peaks (sigma =5), with added noise (Fig. 13). Thin lines represent pure Gaussians (see Table 1); thick line is a resulting spectrum with additive noise (10% of the amplitude of small peaks).

| Peak # | Position | Height | Area |
|---|---|---|---|
| 1 | 50 | 500 | 10159 |
| 2 | 70 | 3000 | 60957 |
| 3 | 80 | 1000 | 20319 |
| 4 | 100 | 5000 | 101596 |
| 5 | 110 | 500 | 10159 |
Table 1 Positions, heights and areas of peaks in the spectrum shown in Fig. 13.
In ideal case, we should obtain the result given in Fig. 14. The areas of the Gaussian components of the spectrum are concentrated completely to delta-functions. When solving the overdetermined system of linear equations with data from Fig. 13 in the sense of minimum least squares criterion without any regularisation we obtain the result with large oscillations (Fig. 15). From mathematical point of view, it is the optimal solution in the unconstrained space of independent variables. From physical point of view we are interested only in a meaningful solution. Therefore, we have to employ regularisation techniques (e.g. Gold deconvolution) and/or to confine the space of allowed solutions to subspace of positive solutions.
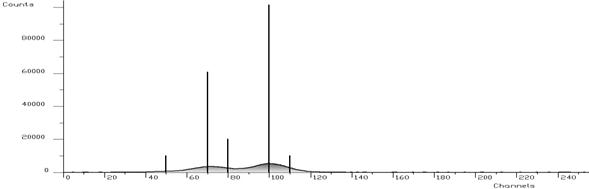
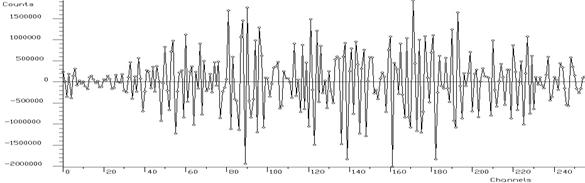
When we employ Gold deconvolution algorithm we obtain the result given in Fig. 16. One can observe that the resulting spectrum is smooth. On the other hand the method is not able to decompose completely the peaks in the spectrum.
Example of Gold deconvolution for closely positioned wide peaks. The original source spectrum is drawn with black color, the spectrum after the deconvolution (10000 iterations) with red color.

Further let us employ boosting operation into deconvolution (Fig. 17).
The original source spectrum is drawn with black color, the spectrum after the deconvolution with red color. Number of iterations = 200, number of repetitions = 50 and boosting coefficient = 1.2.
One can observe that peaks are decomposed practically to delta functions. Number of peaks is correct, positions of big peaks as well as their areas are relatively well estimated. However there is a considerable error in the estimation of the position of small right hand peak.
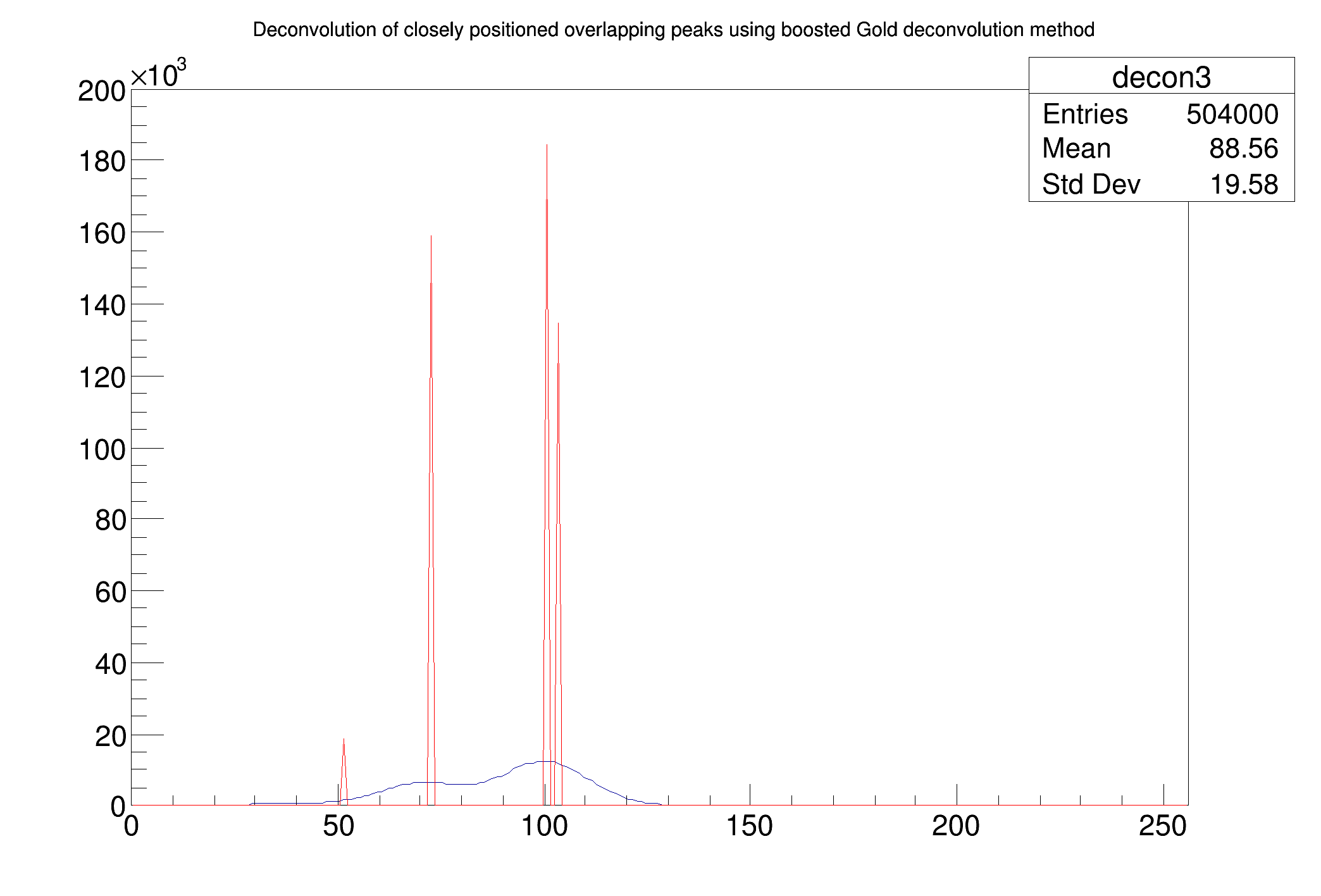
Definition at line 1462 of file TSpectrum.cxx.
| const char * TSpectrum::DeconvolutionRL | ( | Double_t * | source, |
| const Double_t * | response, | ||
| Int_t | ssize, | ||
| Int_t | numberIterations, | ||
| Int_t | numberRepetitions, | ||
| Double_t | boost | ||
| ) |
One-dimensional deconvolution function.
This function calculates deconvolution from source spectrum according to response spectrum using Richardson-Lucy deconvolution algorithm. The result is placed in the vector pointed by source pointer. On successful completion it returns 0. On error it returns pointer to the string describing error. If desired after every numberIterations one can apply boosting operation (exponential function with exponent given by boost coefficient) and repeat it numberRepetitions times (see Gold deconvolution).
For discrete systems it has the form:
\[ x^{(n)}(i) = x^{(n-1)}(i) \sum_{j=0}^{N-1}h(i,j)\frac{y(j)}{\sum_{k=0}^{M-1}h(j,k)x^{(n-1)}(k)} \\ i \in \left<0,M-1\right> \]
for positive input data and response matrix this iterative method forces the deconvoluted spectra to be non-negative. The Richardson-Lucy iteration converges to the maximum likelihood solution for Poisson statistics in the data.
When we employ Richardson-Lucy deconvolution algorithm to our data from Fig. 13 we obtain the following result. One can observe improvements as compared to the result achieved by Gold deconvolution. Nevertheless it is unable to decompose the multiplet.
Example of Richardson-Lucy deconvolution for closely positioned wide peaks. The original source spectrum is drawn with black color, the spectrum after the deconvolution (10000 iterations) with red color.
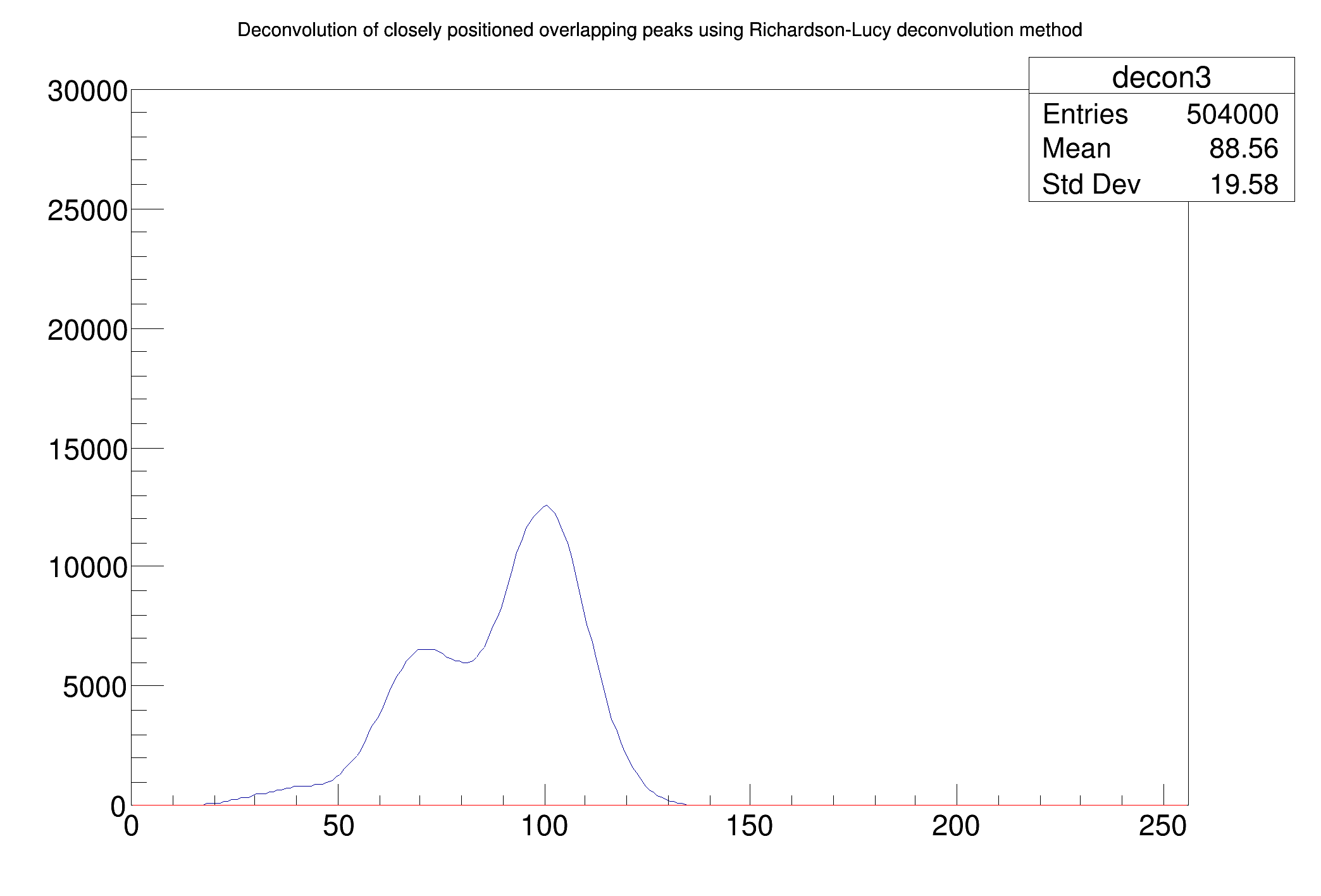
Further let us employ boosting operation into deconvolution.
The original source spectrum is drawn with black color, the spectrum after the deconvolution with red color. Number of iterations = 200, number of repetitions = 50 and boosting coefficient = 1.2.
One can observe improvements in the estimation of peak positions as compared to the results achieved by Gold deconvolution.

Definition at line 1668 of file TSpectrum.cxx.
|
inline |
Definition at line 56 of file TSpectrum.h.
|
inline |
Definition at line 57 of file TSpectrum.h.
|
inline |
Definition at line 58 of file TSpectrum.h.
|
inline |
Definition at line 59 of file TSpectrum.h.
Print the array of positions.
Reimplemented from TNamed.
Definition at line 222 of file TSpectrum.cxx.
|
virtual |
One-dimensional peak search function.
This function searches for peaks in source spectrum in hin The number of found peaks and their positions are written into the members fNpeaks and fPositionX. The search is performed in the current histogram range.
By default, the background is removed before deconvolution. Specify the option "nobackground" to not remove the background.
By default the "Markov" chain algorithm is used. Specify the option "noMarkov" to disable this algorithm Note that by default the source spectrum is replaced by a new spectrum
By default a polymarker object is created and added to the list of functions of the histogram. The histogram is drawn with the specified option and the polymarker object drawn on top of the histogram. The polymarker coordinates correspond to the npeaks peaks found in the histogram.
A pointer to the polymarker object can be retrieved later via:
Specify the option "goff" to disable the storage and drawing of the polymarker.
To disable the final drawing of the histogram with the search results (in case you want to draw it yourself) specify "nodraw" in the options parameter.
Definition at line 269 of file TSpectrum.cxx.
| Int_t TSpectrum::Search1HighRes | ( | Double_t * | source, |
| Double_t * | destVector, | ||
| Int_t | ssize, | ||
| Double_t | sigma, | ||
| Double_t | threshold, | ||
| bool | backgroundRemove, | ||
| Int_t | deconIterations, | ||
| bool | markov, | ||
| Int_t | averWindow | ||
| ) |
Old name of SearcHighRes introduced for back compatibility.
This function will be removed after the June 2006 release
Definition at line 2566 of file TSpectrum.cxx.
| Int_t TSpectrum::SearchHighRes | ( | Double_t * | source, |
| Double_t * | destVector, | ||
| Int_t | ssize, | ||
| Double_t | sigma, | ||
| Double_t | threshold, | ||
| bool | backgroundRemove, | ||
| Int_t | deconIterations, | ||
| bool | markov, | ||
| Int_t | averWindow | ||
| ) |
One-dimensional high-resolution peak search function.
This function searches for peaks in source spectrum. It is based on deconvolution method. First the background is removed (if desired), then Markov smoothed spectrum is calculated (if desired), then the response function is generated according to given sigma and deconvolution is carried out. The order of peaks is arranged according to their heights in the spectrum after background elimination. The highest peak is the first in the list. On success it returns number of found peaks.
The goal of this function is to identify automatically the peaks in spectrum with the presence of the continuous background and statistical fluctuations - noise.
The common problems connected with correct peak identification are:

Examples of peak searching method:
The SearchHighRes function provides users with the possibility to vary the input parameters and with the access to the output deconvolved data in the destination spectrum. Based on the output data one can tune the parameters.
One-dimensional spectrum with found peaks denoted by markers, 3 iterations steps in the deconvolution.
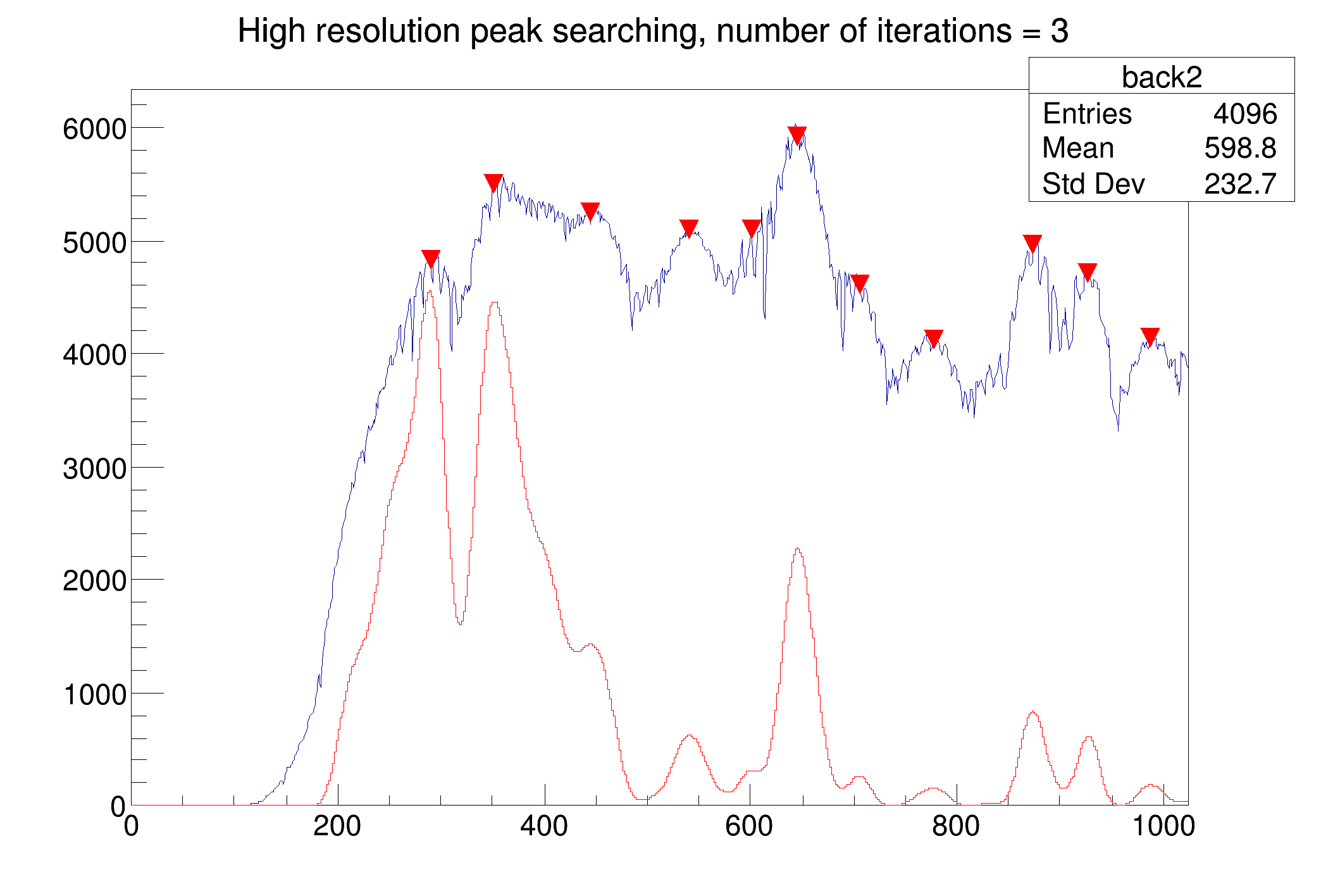
Influence of number of iterations (3-red, 10-blue, 100- green, 1000-magenta), sigma=8, smoothing width=3.
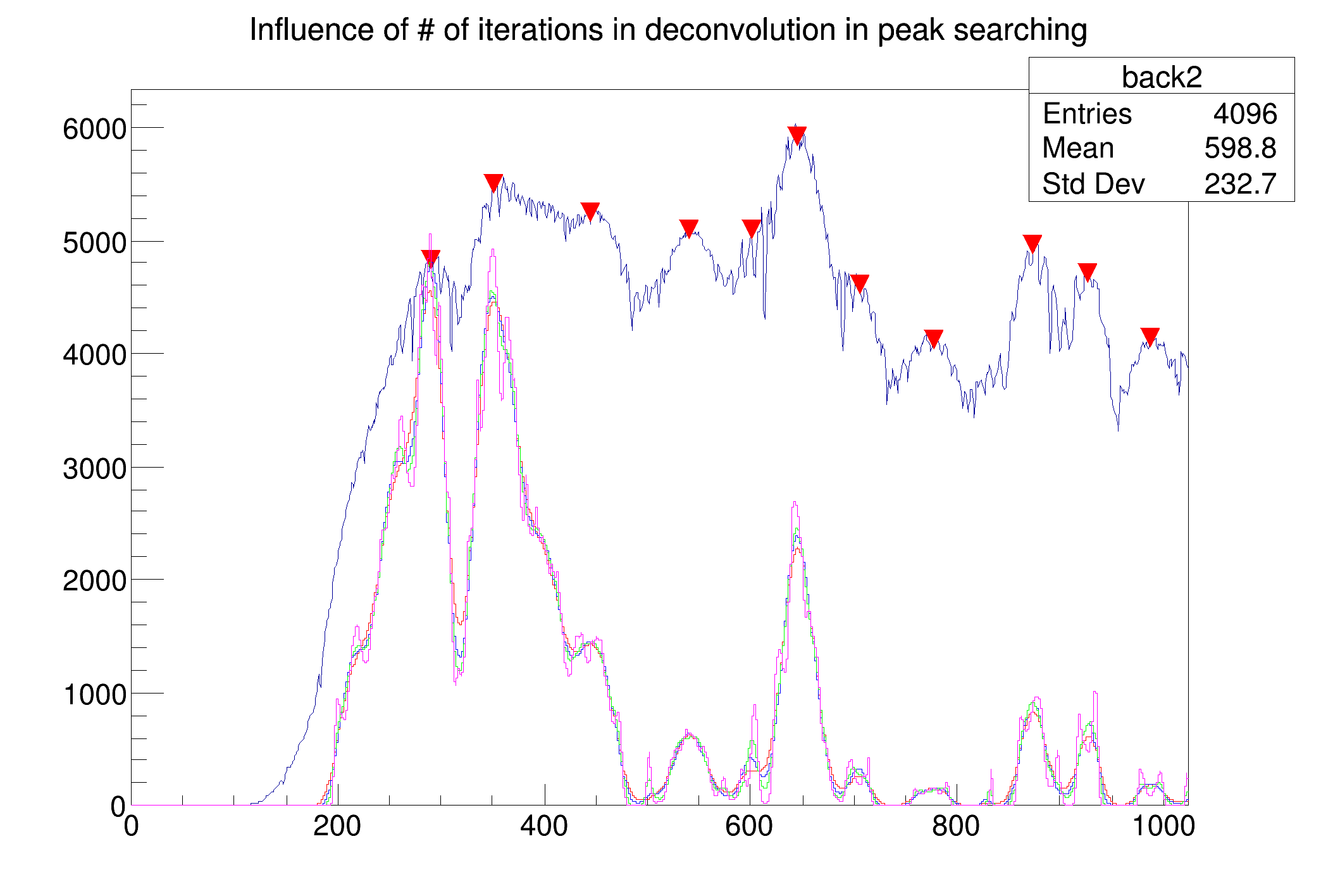
Definition at line 2129 of file TSpectrum.cxx.
Static function: Set average window of searched peaks (see TSpectrum::SearchHighRes).
Definition at line 102 of file TSpectrum.cxx.
Static function: Set max number of decon iterations in deconvolution operation (see TSpectrum::SearchHighRes).
Definition at line 111 of file TSpectrum.cxx.
NOT USED resolution: determines resolution of the neighbouring peaks default value is 1 correspond to 3 sigma distance between peaks.
Higher values allow higher resolution (smaller distance between peaks. May be set later through SetResolution.
Definition at line 354 of file TSpectrum.cxx.
One-dimensional markov spectrum smoothing function.
This function calculates smoothed spectrum from source spectrum based on Markov chain method. The result is placed in the array pointed by source pointer. On successful completion it returns 0. On error it returns pointer to the string describing error.
The goal of this function is the suppression of the statistical fluctuations. The algorithm is based on discrete Markov chain, which has very simple invariant distribution:
\[ U_2 = \frac{p_{1,2}}{p_{2,1}}U_1, U_3 = \frac{p_{2,3}}{p_{3,2}}U_2U_1, ... , U_n = \frac{p_{n-1,n}}{p_{n,n-1}}U_{n-1}...U_2U_1 \]
\( U_1\) being defined from the normalization condition \( \sum_{i=1}^{n} U_i=1\). \( n \) is the length of the smoothed spectrum and
\[ p_{i,i\pm 1} = A_i\sum_{k=1}^{m} exp\left[ \frac{y(i\pm k)-y(i)}{y(i\pm k)+y(i)}\right] \]
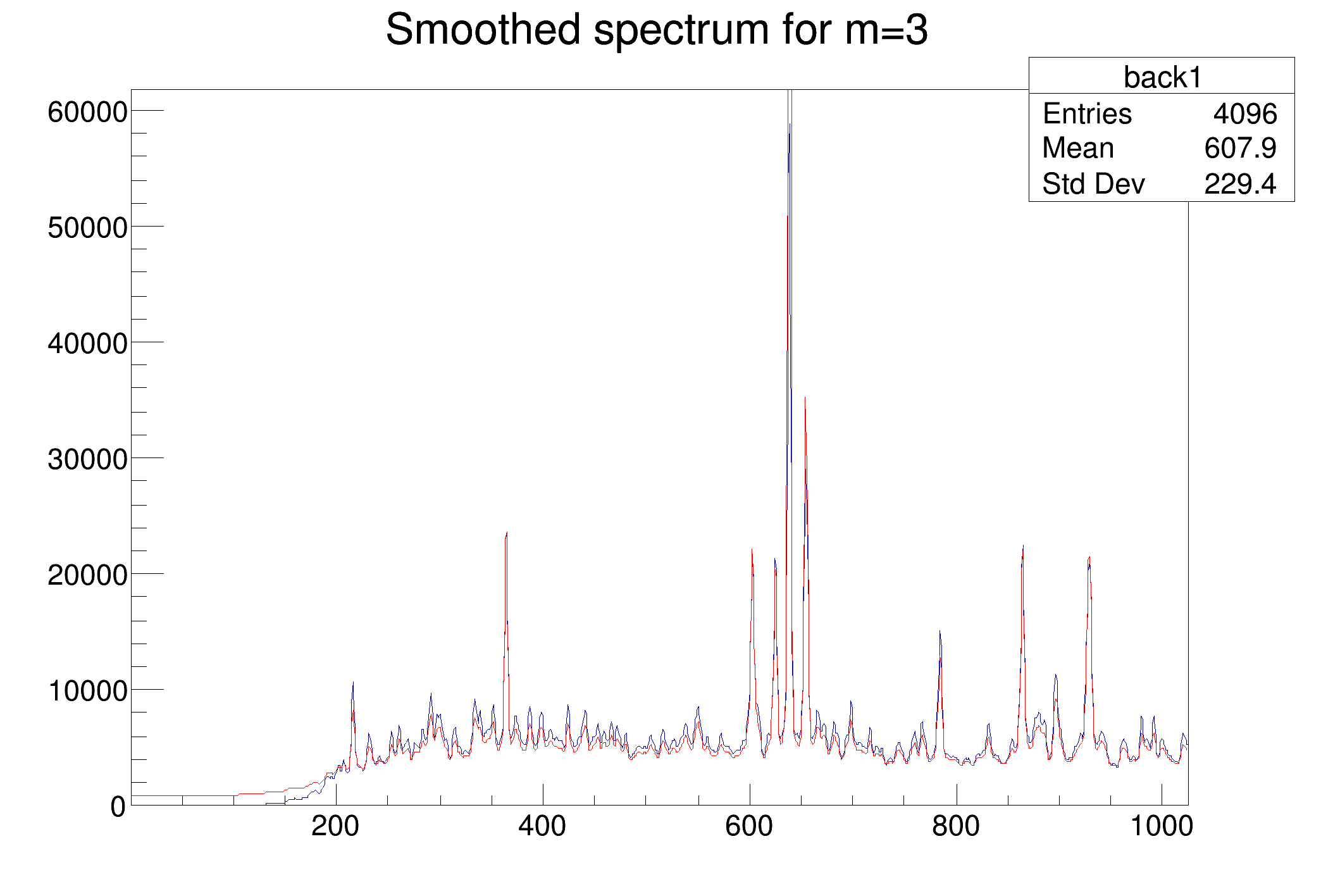
Definition at line 1198 of file TSpectrum.cxx.
|
static |
Static function, interface to TSpectrum::Background.
Definition at line 2590 of file TSpectrum.cxx.
|
static |
Static function, interface to TSpectrum::Search.
Definition at line 2580 of file TSpectrum.cxx.
| const char * TSpectrum::Unfolding | ( | Double_t * | source, |
| const Double_t ** | respMatrix, | ||
| Int_t | ssizex, | ||
| Int_t | ssizey, | ||
| Int_t | numberIterations, | ||
| Int_t | numberRepetitions, | ||
| Double_t | boost | ||
| ) |
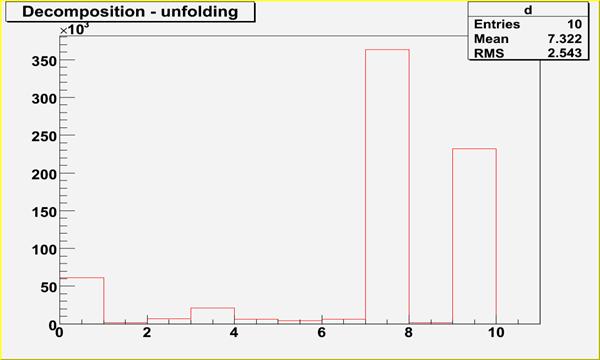
One-dimensional unfolding function.
This function unfolds source spectrum according to response matrix columns. The result is placed in the vector pointed by source pointer. The coefficients of the resulting vector represent contents of the columns (weights) in the input vector. On successful completion it returns 0. On error it returns pointer to the string describing error. If desired after every numberIterations one can apply boosting operation (exponential function with exponent given by boost coefficient) and repeat it numberRepetitions times. For details we refer to [1].
The goal is the decomposition of spectrum to a given set of component spectra.
The mathematical formulation of the discrete linear system is:
\[ y(i) = \sum_{k=0}^{N_y-1} h(i,k)x(k), i = 0,1,2,...,N_x-1 \]
\[ \begin{bmatrix} y(0) \\ y(1) \\ \dots \\ y(N_x-1) \end{bmatrix} = \begin{bmatrix} h(0,0) & h(0,1) & \dots & h(0,N_y-1) \\ h(1,0) & h(1,1) & \dots & h(1,N_y-1) \\ \dots \\ h(N_x-1,0) & h(N_x-1,1) & \dots & h(N_x-1,N_y-1) \end{bmatrix} \begin{bmatrix} x(0) \\ x(1) \\ \dots \\ x(N_y-1) \end{bmatrix} \]


Definition at line 1892 of file TSpectrum.cxx.
|
staticprotected |
Average window of searched peaks.
Definition at line 32 of file TSpectrum.h.
|
staticprotected |
Maximum number of decon iterations (default=3)
Definition at line 33 of file TSpectrum.h.
|
protected |
resulting histogram
Definition at line 31 of file TSpectrum.h.
|
protected |
Maximum number of peaks to be found.
Definition at line 25 of file TSpectrum.h.
|
protected |
number of peaks found
Definition at line 26 of file TSpectrum.h.
|
protected |
[fNPeaks] array of current peak positions
Definition at line 27 of file TSpectrum.h.
|
protected |
[fNPeaks] X position of peaks
Definition at line 28 of file TSpectrum.h.
|
protected |
[fNPeaks] Y position of peaks
Definition at line 29 of file TSpectrum.h.
|
protected |
NOT USED resolution of the neighboring peaks
Definition at line 30 of file TSpectrum.h.