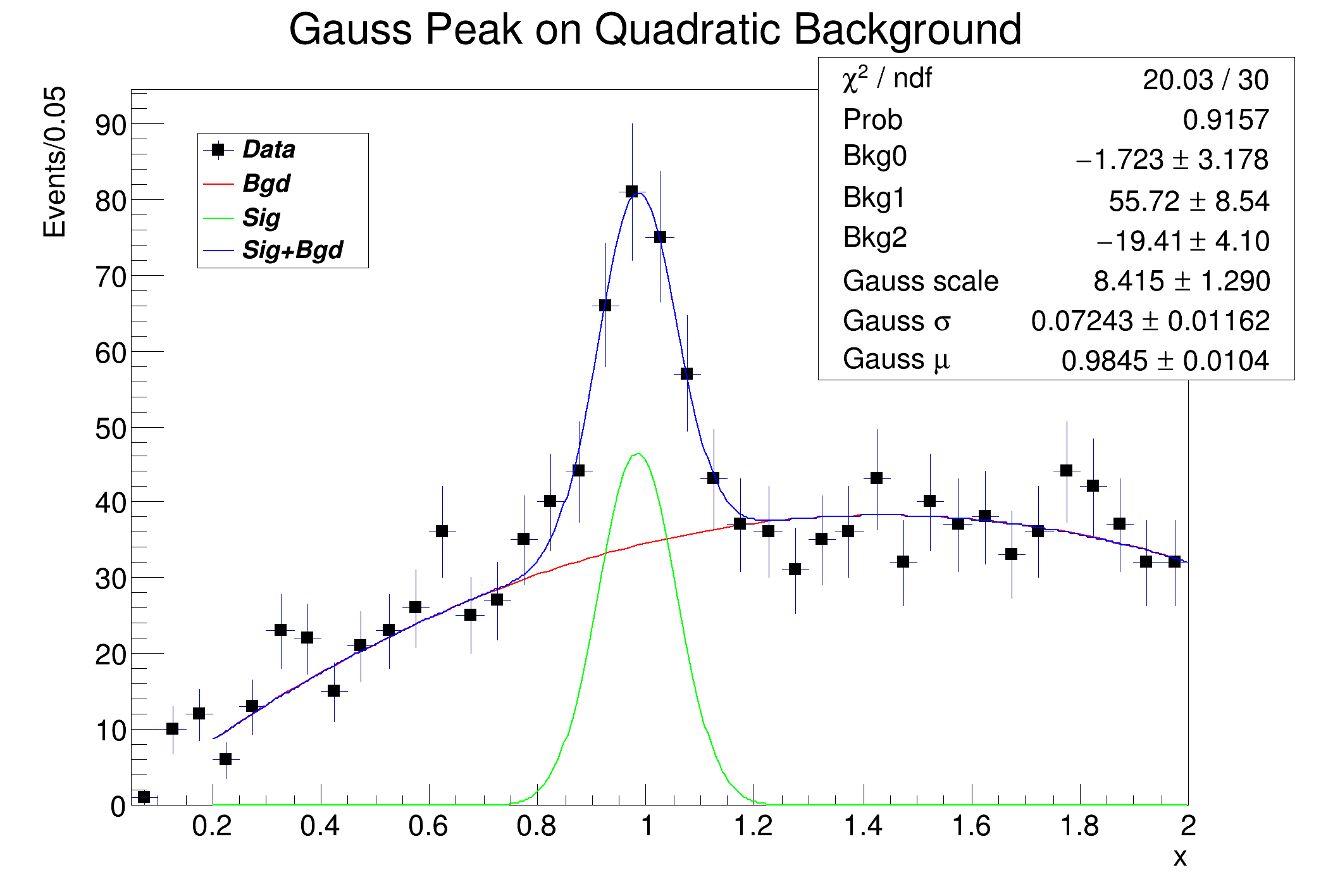
Example for fitting a signal + background model to a histogram found in a file.
enum ParIndex_t {
Bkg0=0, Bkg1=1, Bkg2,
SigScale, SigSigma, SigMean,
N_PAR};
const std::map<ParIndex_t,std::string> parNames{
{Bkg0, "Bkg0"}, {Bkg1, "Bkg1"}, {Bkg2, "Bkg2"},
{SigScale, "Gauss scale"}, {SigSigma, "Gauss #sigma"}, {SigMean, "Gauss #mu"}
};
return par[Bkg0] + par[Bkg1]*
x[0] + par[Bkg2]*
x[0]*
x[0];
}
return par[SigScale]*
TMath::Gaus(
x[0], par[SigMean], par[SigSigma],
true);
}
return background(
x, par) + signal(
x, par);
}
TF1 fitFcn(
"fitFcn",fitFunction,fitxmin,fitxmax,N_PAR);
fitFcn.SetNpx(500);
fitFcn.SetLineWidth(2);
fitFcn.SetLineColor(
kBlue);
for (auto& idx_name : parNames) {
fitFcn.SetParName(idx_name.first, idx_name.second.c_str());
}
fitFcn.SetParameters(30,0,0,50.,0.1,1.);
histo->
Fit(
"fitFcn",
"VR+",
"ep");
TF1 backFcn(
"backFcn",background,fitxmin,fitxmax,N_PAR);
backFcn.SetLineColor(
kRed);
TF1 signalFcn(
"signalFcn",signal,fitxmin,fitxmax,N_PAR);
signalFcn.SetLineColor(
kBlue);
signalFcn.SetNpx(500);
fitFcn.GetParameters(par);
backFcn.SetParameters(par);
backFcn.DrawCopy("same");
signalFcn.SetParameters(par);
signalFcn.SetLineColor(
kGreen);
signalFcn.DrawCopy("same");
const double integral = signalFcn.Integral(0.,3.);
cout << "number of signal events = " << integral/binwidth << " " << binwidth<< endl;
TLegend legend(0.15,0.7,0.28,0.85);
legend.SetTextFont(72);
legend.SetTextSize(0.03);
legend.AddEntry(histo,"Data","lpe");
legend.AddEntry(&backFcn,"Bgd","l");
legend.AddEntry(&signalFcn,"Sig","l");
legend.AddEntry(&fitFcn,"Sig+Bgd","l");
legend.DrawClone();
}
void CreateRootFile(){
const int nBins = 60;
Double_t data[nBins] = { 6, 1,10,12, 6,13,23,22,15,21,
23,26,36,25,27,35,40,44,66,81,
75,57,43,37,36,31,35,36,43,32,
40,37,38,33,36,44,42,37,32,32,
43,44,35,33,33,39,29,41,32,44,
26,39,29,35,32,21,21,15,25,15};
TFile*
f =
new TFile(
"exampleRootFile.root",
"RECREATE");
TH1D *histo =
new TH1D(
"histo",
"Gauss Peak on Quadratic Background;x;Events/0.05",60,0,3);
}
void FitHistoInFile() {
float fitxmin=0.2;
float fitxmax=2.7;
TCanvas *
c1 =
new TCanvas(
"c1",
"Fitting Demo of Histogram in File",10,10,700,500);
CreateRootFile();
f->GetObject(
"histo",histo);
if (!histo){
cout << "histo not found"<<endl;
return;
}
FitRoutine(
c1,histo, fitxmin, fitxmax,
"FitHistoInFile.pdf");
}
R__EXTERN TStyle * gStyle
virtual void SetMarkerStyle(Style_t mstyle=1)
Set the marker style.
virtual void SetMarkerSize(Size_t msize=1)
Set the marker size.
virtual void SetRange(Int_t first=0, Int_t last=0)
Set the viewing range for the axis using bin numbers.
virtual Double_t GetBinWidth(Int_t bin) const
Return bin width.
A ROOT file is a suite of consecutive data records (TKey instances) with a well defined format.
1-D histogram with a double per channel (see TH1 documentation)}
TH1 is the base class of all histogram classes in ROOT.
TAxis * GetXaxis()
Get the behaviour adopted by the object about the statoverflows. See EStatOverflows for more informat...
virtual TFitResultPtr Fit(const char *formula, Option_t *option="", Option_t *goption="", Double_t xmin=0, Double_t xmax=0)
Fit histogram with function fname.
virtual void SetBinContent(Int_t bin, Double_t content)
Set bin content see convention for numbering bins in TH1::GetBin In case the bin number is greater th...
virtual void Draw(Option_t *option="")
Draw this histogram with options.
This class displays a legend box (TPaveText) containing several legend entries.
void SetOptStat(Int_t stat=1)
The type of information printed in the histogram statistics box can be selected via the parameter mod...
void SetOptFit(Int_t fit=1)
The type of information about fit parameters printed in the histogram statistics box can be selected ...
Double_t Gaus(Double_t x, Double_t mean=0, Double_t sigma=1, Bool_t norm=kFALSE)
Calculate a gaussian function with mean and sigma.
**********
** 1 **SET PRINT 2
**********
**********
** 2 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 Bkg0 3.00000e+01 9.00000e+00 no limits
2 Bkg1 0.00000e+00 3.00000e-01 no limits
3 Bkg2 0.00000e+00 3.00000e-01 no limits
4 Gauss scale 5.00000e+01 1.50000e+01 no limits
5 Gauss #sigma 1.00000e-01 3.00000e-02 no limits
6 Gauss #mu 1.00000e+00 3.00000e-01 no limits
**********
** 3 **SET ERR 1
**********
**********
** 4 **SET PRINT 2
**********
**********
** 5 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 6 **MIGRAD 1780 0.01
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-05
FCN=1529.1 FROM MIGRAD STATUS=INITIATE 24 CALLS 25 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 Bkg0 3.00000e+01 9.00000e+00 9.00000e+00 3.89571e+01
2 Bkg1 0.00000e+00 3.00000e-01 3.00000e-01 2.48243e+01
3 Bkg2 0.00000e+00 3.00000e-01 3.00000e-01 1.67398e+01
4 Gauss scale 5.00000e+01 1.50000e+01 1.50000e+01 6.90295e+01
5 Gauss #sigma 1.00000e-01 3.00000e-02 3.00000e-02 -1.07955e+04
6 Gauss #mu 1.00000e+00 3.00000e-01 3.00000e-01 1.46740e+03
NO ERROR MATRIX
FCN=417.624 FROM MIGRAD STATUS=PROGRESS 40 CALLS 41 TOTAL
EDM=1920.53 STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 Bkg0 2.10028e+01 9.00000e+00 -8.99723e+00 -1.37600e+01
2 Bkg1 -4.96702e+00 3.00000e-01 -4.96702e+00 -3.10866e+01
3 Bkg2 -1.39455e+00 3.00000e-01 -1.39455e+00 -5.58507e+01
4 Gauss scale 2.71085e+01 1.50000e+01 -2.28915e+01 1.28566e+01
5 Gauss #sigma 1.22430e-01 3.00000e-02 2.24305e-02 -1.94518e+03
6 Gauss #mu 9.95333e-01 3.00000e-01 -4.66700e-03 -1.69092e+02
FCN=21.0419 FROM MIGRAD STATUS=PROGRESS 193 CALLS 194 TOTAL
EDM=0.217986 STRATEGY= 1 ERROR MATRIX UNCERTAINTY 11.2 per cent
EXT PARAMETER APPROXIMATE STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 Bkg0 -2.93549e+00 3.26899e+00 -4.04489e-01 -1.97901e-01
2 Bkg1 5.77085e+01 9.12472e+00 4.78059e-01 2.16368e-01
3 Bkg2 -2.01524e+01 4.38963e+00 -1.73849e-02 3.13786e-01
4 Gauss scale 8.78327e+00 1.27122e+00 -1.32160e-01 7.78317e-02
5 Gauss #sigma 8.19441e-02 8.06154e-03 -2.26106e-03 1.37176e+02
6 Gauss #mu 9.80776e-01 1.18681e-02 -3.58341e-03 -4.16629e+01
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
START COVARIANCE MATRIX CALCULATION.
EIGENVALUES OF SECOND-DERIVATIVE MATRIX:
5.7258e-03 2.8804e-01 5.3283e-01 9.8675e-01 1.4293e+00 2.7574e+00
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=20.0331 FROM MIGRAD STATUS=CONVERGED 290 CALLS 291 TOTAL
EDM=2.69165e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 Bkg0 -1.72294e+00 3.17849e+00 1.99347e-03 4.66320e-04
2 Bkg1 5.57228e+01 8.54024e+00 1.85549e-03 7.24658e-04
3 Bkg2 -1.94083e+01 4.09693e+00 1.19727e-03 1.12459e-03
4 Gauss scale 8.41522e+00 1.29039e+00 2.13143e-03 -1.25112e-04
5 Gauss #sigma 7.24347e-02 1.16170e-02 2.10634e-05 1.14937e-02
6 Gauss #mu 9.84485e-01 1.04307e-02 2.32047e-05 1.27105e-02
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 6 ERR DEF=1
1.010e+01 -2.478e+01 1.103e+01 1.400e+00 9.194e-03 1.986e-04
-2.478e+01 7.294e+01 -3.441e+01 -5.378e+00 -3.588e-02 1.763e-03
1.103e+01 -3.441e+01 1.678e+01 2.584e+00 1.727e-02 -1.280e-03
1.400e+00 -5.378e+00 2.584e+00 1.665e+00 8.489e-03 -4.402e-04
9.194e-03 -3.588e-02 1.727e-02 8.489e-03 1.350e-04 -1.120e-05
1.986e-04 1.763e-03 -1.280e-03 -4.402e-04 -1.120e-05 1.088e-04
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2 3 4 5 6
1 0.95998 1.000 -0.913 0.847 0.341 0.249 0.006
2 0.99528 -0.913 1.000 -0.983 -0.488 -0.362 0.020
3 0.99145 0.847 -0.983 1.000 0.489 0.363 -0.030
4 0.67502 0.341 -0.488 0.489 1.000 0.566 -0.033
5 0.58545 0.249 -0.362 0.363 0.566 1.000 -0.092
6 0.11073 0.006 0.020 -0.030 -0.033 -0.092 1.000
EXTERNAL ERROR MATRIX. NDIM= 6 NPAR= 6 ERR DEF=1
1.010e+01 -2.478e+01 1.103e+01 1.400e+00 9.194e-03 1.986e-04
-2.478e+01 7.294e+01 -3.441e+01 -5.378e+00 -3.588e-02 1.763e-03
1.103e+01 -3.441e+01 1.678e+01 2.584e+00 1.727e-02 -1.280e-03
1.400e+00 -5.378e+00 2.584e+00 1.665e+00 8.489e-03 -4.402e-04
9.194e-03 -3.588e-02 1.727e-02 8.489e-03 1.350e-04 -1.120e-05
1.986e-04 1.763e-03 -1.280e-03 -4.402e-04 -1.120e-05 1.088e-04
FCN=20.0331 FROM MIGRAD STATUS=CONVERGED 290 CALLS 291 TOTAL
EDM=2.69165e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER PARABOLIC MINOS ERRORS
NO. NAME VALUE ERROR NEGATIVE POSITIVE
1 Bkg0 -1.72294e+00 3.17849e+00
2 Bkg1 5.57228e+01 8.54024e+00
3 Bkg2 -1.94083e+01 4.09693e+00
4 Gauss scale 8.41522e+00 1.29039e+00
5 Gauss #sigma 7.24347e-02 1.16170e-02
6 Gauss #mu 9.84485e-01 1.04307e-02
number of signal events = 168.304 0.05