A common method used in High Energy Physics to perform measurements is the maximum Likelihood method, exploiting discriminating variables to disentangle signal from background.

The crucial point for such an analysis to be reliable is to use an exhaustive list of sources of events combined with an accurate description of all the Probability Density Functions (PDF).

To assess the validity of the fit, a convincing quality check is to explore further the data sample by examining the distributions of control variables. A control variable can be obtained for instance by removing one of the discriminating variables before performing again the maximum Likelihood fit: this removed variable is a control variable. The expected distribution of this control variable, for signal, is to be compared to the one extracted, for signal, from the data sample. In order to be able to do so, one must be able to unfold from the distribution of the whole data sample.

The TSPlot method allows to reconstruct the distributions for the control variable, independently for each of the various sources of events, without making use of any a priori knowledge on this variable. The aim is thus to use the knowledge available for the discriminating variables to infer the behaviour of the individual sources of events with respect to the control variable.

TSPlot is optimal if the control variable is uncorrelated with the discriminating variables.

A detail description of the formalism itself, called $\hbox{$_s$}{\cal P}lot$, is given in [1].

The method

The $\hbox{$_s$}{\cal P}lot$ technique is developed in the above context of a maximum Likelihood method making use of discriminating variables.

One considers a data sample in which are merged several species of events. These species represent various signal components and background components which all together account for the data sample. The different terms of the log-Likelihood are:

$N$ : the total number of events in the data sample,
${\rm N}_{\rm s}$ : the number of species of events populating the data sample,
$N_i$ : the number of events expected on the average for the $i^{\rm th}$ species,
${\rm f}_i(y_e)$" : the value of the PDFs of the discriminating variables \_form#829" for the\f$i^{th}\f$ species and for event\f$e\f$", - \_form#524" : the set of control variables which, by definition, do not appear in the expression of the Likelihood function ${\cal L}$.

The extended log-Likelihood reads:

\[ {\cal L}=\sum_{e=1}^{N}\ln \Big\{ \sum_{i=1}^{{\rm N}_{\rm s}}N_i{\rm f}_i(y_e) \Big\} -\sum_{i=1}^{{\rm N}_{\rm s}}N_i \tag{1} \]

From this expression, after maximization of ${\cal L}$ with respect to the $N_i$ parameters, a weight can be computed for every event and each species, in order to obtain later the true distribution $\hbox{M}_i(x)$ of variable $x$. If ${\rm n}$ is one of the ${\rm N}_{\rm s}$ species present in the data sample, the weight for this species is defined by:

\[ \fbox{$ {_s{\cal P}}_{\rm n}(y_e)={\sum_{j=1}^{{\rm N}_{\rm s}} \hbox{V}_{{\rm n}j}{\rm f}_j(y_e)\over\sum_{k=1}^{{\rm N}_{\rm s}}N_k{\rm f}_k(y_e) } $} , \tag{2} \]

where $\hbox{V}_{{\rm n}j}$

is the covariance matrix resulting from the Likelihood maximization. This matrix can be used directly from the fit, but this is numerically less accurate than the direct computation:

\[ \hbox{ V}^{-1}_{{\rm n}j}~=~ {\partial^2(-{\cal L})\over\partial N_{\rm n}\partial N_j}~=~ \sum_{e=1}^N {{\rm f}_{\rm n}(y_e){\rm f}_j(y_e)\over(\sum_{k=1}^{{\rm N}_{\rm s}}N_k{\rm f}_k(y_e))^2} . \tag{3} \]

The distribution of the control variable $x$ obtained by histogramming the weighted events reproduces, on average, the true distribution ${\hbox{ {M}}}_{\rm n}(x)$

The class TSPlot allows to reconstruct the true distribution ${\hbox{ {M}}}_{\rm n}(x)$

of a control variable $x$ for each of the ${\rm N}_{\rm s}$ species from the sole knowledge of the PDFs of the discriminating variables ${\rm f}_i(y)$. The plots obtained thanks to the TSPlot class are called $\hbox {$_s$}{\cal P}lots$.

Some properties and checks

Beside reproducing the true distribution, $\hbox {$_s$}{\cal P}lots$ bear remarkable properties:

Each $x$ - distribution is properly normalized:

\[ \sum_{e=1}^{N} {_s{\cal P}}_{\rm n}(y_e)~=~N_{\rm n} ~. \tag{4} \]

For any event:

\[ \sum_{l=1}^{{\rm N}_{\rm s}} {_s{\cal P}}_l(y_e) ~=~1 ~. \tag{5} \]

That is to say that, summing up the \f${\rm N}_{\rm s}\f$ \f$\hbox {$_s$}{\cal P}lots\f$,
one recovers the data sample distribution in \f$x\f$, and summing up the number of events
entering in a \f$\hbox{$_s$}{\cal P}lot\f$ for a given species, one recovers the yield of the
species, as provided by the fit.
The property <a href="http://www.slac.stanford.edu/%7Epivk/sPlot/sPlot_ROOT/sPlot_ROOT.html#eq:NormalizationOK">4</a> is implemented in the TSPlot class as a check.

the sum of the statistical uncertainties per bin

\[ \sigma[N_{\rm n}\ _s\tilde{\rm M}_{\rm n}(x) {\delta x}]~=~\sqrt{\sum_{e \subset {\delta x}} ({_s{\cal P}}_{\rm n})^2} ~. \tag{6} \]

reproduces the statistical uncertainty on the yield \f$N_{\rm n}\f$, as provided by the fit:
\f$\sigma[N_{\rm n}]\equiv\sqrt{\hbox{ V}_{{\rm n}{\rm n}}}\f$ .
Because of that and since the determination of the yields is optimal
when obtained using a Likelihood fit, one can conclude that the \f$\hbox{$_s$}{\cal P}lot\f$
technique is itself an optimal method to reconstruct distributions of control variables.

Different steps followed by TSPlot

A maximum Likelihood fit is performed to obtain the yields $N_i$ of the various species.The fit relies on discriminating variables $y$ uncorrelated with a control variable $x$: the later is therefore totally absent from the fit.
The weights ${_s{\cal P}}$ are calculated using Eq. (2) where the covariance matrix is taken from Minuit.
Histograms of $x$ are filled by weighting the events with ${_s{\cal P}}$ .
Error bars per bin are given by Eq. (6).

The $\hbox {$_s$}{\cal P}lots$ reproduce the true distributions of the species in the control variable $x$, within the above defined statistical uncertainties.

Illustrations

To illustrate the technique, one considers an example derived from the analysis where $\hbox {$_s$}{\cal P}lots$ have been first used (charmless B decays). One is dealing with a data sample in which two species are present: the first is termed signal and the second background. A maximum Likelihood fit is performed to obtain the two yields $N_1$ and $N_2$ . The fit relies on two discriminating variables collectively denoted $y$ which are chosen within three possible variables denoted ${m_{\rm ES}}$ , $\Delta E$ and ${\cal F}$. The variable which is not incorporated in $y$ is used as the control variable $x$ . The six distributions of the three variables are assumed to be the ones depicted in Fig. 1.

Figure 1:

Distributions of the three discriminating variables available to perform the Likelihood fit: ${m_{\rm ES}}$ , $\Delta E$ , ${\cal F}$ . Among the three variables, two are used to perform the fit while one is kept out of the fit to serve the purpose of a control variable. The three distributions on the top (resp. bottom) of the figure correspond to the signal (resp. background). The unit of the vertical axis is chosen such that it indicates the number of entries per bin, if one slices the histograms in 25 bins.

A data sample being built through a Monte Carlo simulation based on the distributions shown in Fig. 1, one obtains the three distributions of Fig. 2. Whereas the distribution of $\Delta E$ clearly indicates the presence of the signal, the distribution of ${m_{\rm ES}}$ and ${\cal F}$ are less obviously populated by signal.

Figure 2:

Distributions of the three discriminating variables for signal plus background. The three distributions are the ones obtained from a data sample obtained through a Monte Carlo simulation based on the distributions shown in Fig. 1. The data sample consists of 500 signal events and 5000 background events.

Choosing $\Delta E$ and ${\cal F}$ as discriminating variables to determine $N_1$ and $N_2$ through a maximum Likelihood fit, one builds, for the control variable ${m_{\rm ES}}$ which is unknown to the fit, the two $\hbox {$_s$}{\cal P}lots$ for signal and background shown in Fig. 3. One observes that the $\hbox{$_s$}{\cal P}lot$ for signal reproduces correctly the PDF even where the latter vanishes, although the error bars remain sizeable. This results from the almost complete cancellation between positive and negative weights: the sum of weights is close to zero while the sum of weights squared is not. The occurence of negative weights occurs through the appearance of the covariance matrix, and its negative components, in the definition of Eq. (2).

A word of caution is in order with respect to the error bars. Whereas their sum in quadrature is identical to the statistical uncertainties of the yields determined by the fit, and if, in addition, they are asymptotically correct, the error bars should be handled with care for low statistics and/or for too fine binning. This is because the error bars do not incorporate two known properties of the PDFs: PDFs are positive definite and can be non-zero in a given x-bin, even if in the particular data sample at hand, no event is observed in this bin. The latter limitation is not specific to $\hbox {$_s$}{\cal P}lots$ , rather it is always present when one is willing to infer the PDF at the origin of an histogram, when, for some bins, the number of entries does not guaranty the applicability of the Gaussian regime. In such situations, a satisfactory practice is to attach allowed ranges to the histogram to indicate the upper and lower limits of the PDF value which are consistent with the actual observation, at a given confidence level.

Figure 3:

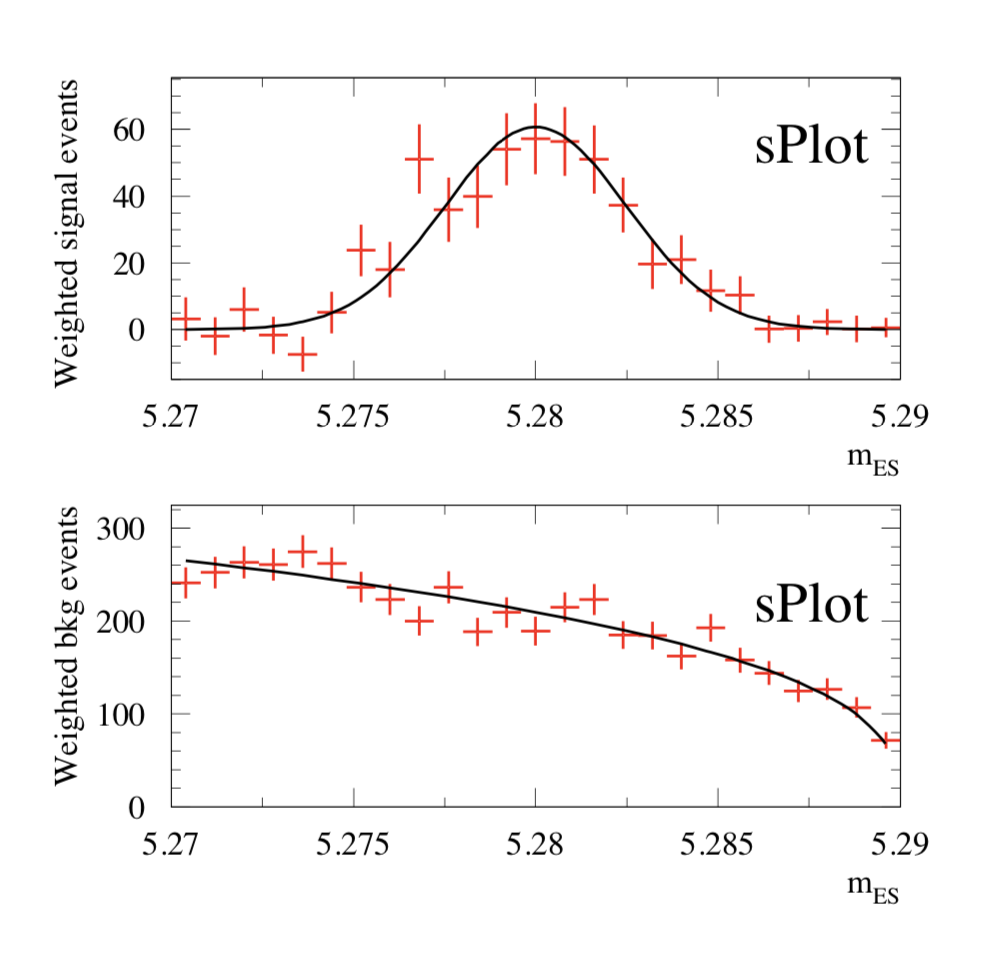
The $\hbox {$_s$}{\cal P}lots$ (signal on top, background on bottom) obtained for ${m_{\rm ES}}$ are represented as dots with error bars. They are obtained from a fit using only information from $\Delta E$ and ${\cal F}$

Choosing ${m_{\rm ES}}$ and $\Delta E$ as discriminating variables to determine $N_1$ and $N_2$ through a maximum Likelihood fit, one builds, for the control variable ${\cal F}$ which is unknown to the fit, the two $\hbox {$_s$}{\cal P}lots$ for signal and background shown in Fig. 4. In the $\hbox{$_s$}{\cal P}lot$ for signal one observes that error bars are the largest in the $x$ regions where the background is the largest.

Figure 4:

The $\hbox {$_s$}{\cal P}lots$ (signal on top, background on bottom) obtained for ${\cal F}$ are represented as dots with error bars. They are obtained from a fit using only information from ${m_{\rm ES}}$ and $\Delta E$

The results above can be obtained by running the tutorial TestSPlot.C

Definition at line 21 of file TSPlot.h.

Public Member Functions
	TSPlot ()
	default constructor (used by I/O only)

	TSPlot (Int_t nx, Int_t ny, Int_t ne, Int_t ns, TTree *tree)
	Normal TSPlot constructor.

virtual	~TSPlot ()
	Destructor.

void	Browse (TBrowser *b)
	To browse the histograms.

void	FillSWeightsHists (Int_t nbins=50)
	The order of histograms in the array:

void	FillXvarHists (Int_t nbins=100)
	Fills the histograms of x variables (not weighted) with nbins.

void	FillYpdfHists (Int_t nbins=100)
	Fills the histograms of pdf-s of y variables with binning nbins.

void	FillYvarHists (Int_t nbins=100)
	Fill the histograms of y variables.

Int_t	GetNevents ()

Int_t	GetNspecies ()

void	GetSWeights (Double_t *weights)
	Returns the matrix of sweights.

void	GetSWeights (TMatrixD &weights)
	Returns the matrix of sweights.

TH1D *	GetSWeightsHist (Int_t ixvar, Int_t ispecies, Int_t iyexcl=-1)
	Returns the histogram of a variable, weighted with sWeights.

TObjArray *	GetSWeightsHists ()
	Returns an array of all histograms of variables, weighted with sWeights.

TString *	GetTreeExpression ()

TString *	GetTreeName ()

TString *	GetTreeSelection ()

TH1D *	GetXvarHist (Int_t ixvar)
	Returns the histogram of variable ixvar.

TObjArray *	GetXvarHists ()
	Returns the array of histograms of x variables (not weighted).

TH1D *	GetYpdfHist (Int_t iyvar, Int_t ispecies)
	Returns the histogram of the pdf of variable iyvar for species #ispecies, binning nbins.

TObjArray *	GetYpdfHists ()
	Returns the array of histograms of pdf's of y variables with binning nbins.

TH1D *	GetYvarHist (Int_t iyvar)
	Returns the histogram of variable iyvar.If histograms have not already been filled, they are filled with default binning 100.

TObjArray *	GetYvarHists ()
	Returns the array of histograms of y variables.

Bool_t	IsFolder () const
	Returns kTRUE in case object contains browsable objects (like containers or lists of other objects).

void	MakeSPlot (Option_t *option="v")
	Calculates the sWeights.

void	RefillHist (Int_t type, Int_t var, Int_t nbins, Double_t min, Double_t max, Int_t nspecies=-1)
	The Fill...Hist() methods fill the histograms with the real limits on the variables This method allows to refill the specified histogram with user-set boundaries min and max.

void	SetInitialNumbersOfSpecies (Int_t *numbers)
	Set the initial number of events of each species - used as initial estimates in minuit.

void	SetNEvents (Int_t ne)

void	SetNSpecies (Int_t ns)

void	SetNX (Int_t nx)

void	SetNY (Int_t ny)

void	SetTree (TTree *tree)
	Set the input Tree.

void	SetTreeSelection (const char varexp="", const char selection="", Long64_t firstentry=0)
	Specifies the variables from the tree to be used for splot.

Public Member Functions inherited from TObject
	TObject ()
	TObject constructor.

	TObject (const TObject &object)
	TObject copy ctor.

virtual	~TObject ()
	TObject destructor.

void	AbstractMethod (const char *method) const
	Use this method to implement an "abstract" method that you don't want to leave purely abstract.

virtual void	AppendPad (Option_t *option="")
	Append graphics object to current pad.

ULong_t	CheckedHash ()
	Check and record whether this class has a consistent Hash/RecursiveRemove setup (*) and then return the regular Hash value for this object.

virtual const char *	ClassName () const
	Returns name of class to which the object belongs.

virtual void	Clear (Option_t *="")

virtual TObject *	Clone (const char *newname="") const
	Make a clone of an object using the Streamer facility.

virtual Int_t	Compare (const TObject *obj) const
	Compare abstract method.

virtual void	Copy (TObject &object) const
	Copy this to obj.

virtual void	Delete (Option_t *option="")
	Delete this object.

virtual Int_t	DistancetoPrimitive (Int_t px, Int_t py)
	Computes distance from point (px,py) to the object.

virtual void	Draw (Option_t *option="")
	Default Draw method for all objects.

virtual void	DrawClass () const
	Draw class inheritance tree of the class to which this object belongs.

virtual TObject *	DrawClone (Option_t *option="") const
	Draw a clone of this object in the current selected pad for instance with: `gROOT->SetSelectedPad(gPad)`.

virtual void	Dump () const
	Dump contents of object on stdout.

virtual void	Error (const char method, const char msgfmt,...) const
	Issue error message.

virtual void	Execute (const char method, const char params, Int_t *error=0)
	Execute method on this object with the given parameter string, e.g.

virtual void	Execute (TMethod method, TObjArray params, Int_t *error=0)
	Execute method on this object with parameters stored in the TObjArray.

virtual void	ExecuteEvent (Int_t event, Int_t px, Int_t py)
	Execute action corresponding to an event at (px,py).

virtual void	Fatal (const char method, const char msgfmt,...) const
	Issue fatal error message.

virtual TObject *	FindObject (const char *name) const
	Must be redefined in derived classes.

virtual TObject *	FindObject (const TObject *obj) const
	Must be redefined in derived classes.

virtual Option_t *	GetDrawOption () const
	Get option used by the graphics system to draw this object.

virtual const char *	GetIconName () const
	Returns mime type name of object.

virtual const char *	GetName () const
	Returns name of object.

virtual char *	GetObjectInfo (Int_t px, Int_t py) const
	Returns string containing info about the object at position (px,py).

virtual Option_t *	GetOption () const

virtual const char *	GetTitle () const
	Returns title of object.

virtual UInt_t	GetUniqueID () const
	Return the unique object id.

virtual Bool_t	HandleTimer (TTimer *timer)
	Execute action in response of a timer timing out.

virtual ULong_t	Hash () const
	Return hash value for this object.

Bool_t	HasInconsistentHash () const
	Return true is the type of this object is known to have an inconsistent setup for Hash and RecursiveRemove (i.e.

virtual void	Info (const char method, const char msgfmt,...) const
	Issue info message.

virtual Bool_t	InheritsFrom (const char *classname) const
	Returns kTRUE if object inherits from class "classname".

virtual Bool_t	InheritsFrom (const TClass *cl) const
	Returns kTRUE if object inherits from TClass cl.

virtual void	Inspect () const
	Dump contents of this object in a graphics canvas.

void	InvertBit (UInt_t f)

virtual Bool_t	IsEqual (const TObject *obj) const
	Default equal comparison (objects are equal if they have the same address in memory).

R__ALWAYS_INLINE Bool_t	IsOnHeap () const

virtual Bool_t	IsSortable () const

R__ALWAYS_INLINE Bool_t	IsZombie () const

virtual void	ls (Option_t *option="") const
	The ls function lists the contents of a class on stdout.

void	MayNotUse (const char *method) const
	Use this method to signal that a method (defined in a base class) may not be called in a derived class (in principle against good design since a child class should not provide less functionality than its parent, however, sometimes it is necessary).

virtual Bool_t	Notify ()
	This method must be overridden to handle object notification.

void	Obsolete (const char method, const char asOfVers, const char *removedFromVers) const
	Use this method to declare a method obsolete.

void	operator delete (void *ptr)
	Operator delete.

void	operator delete[] (void *ptr)
	Operator delete [].

void *	operator new (size_t sz)

void *	operator new (size_t sz, void *vp)

void *	operator new[] (size_t sz)

void *	operator new[] (size_t sz, void *vp)

TObject &	operator= (const TObject &rhs)
	TObject assignment operator.

virtual void	Paint (Option_t *option="")
	This method must be overridden if a class wants to paint itself.

virtual void	Pop ()
	Pop on object drawn in a pad to the top of the display list.

virtual void	Print (Option_t *option="") const
	This method must be overridden when a class wants to print itself.

virtual Int_t	Read (const char *name)
	Read contents of object with specified name from the current directory.

virtual void	RecursiveRemove (TObject *obj)
	Recursively remove this object from a list.

void	ResetBit (UInt_t f)

virtual void	SaveAs (const char filename="", Option_t option="") const
	Save this object in the file specified by filename.

virtual void	SavePrimitive (std::ostream &out, Option_t *option="")
	Save a primitive as a C++ statement(s) on output stream "out".

void	SetBit (UInt_t f)

void	SetBit (UInt_t f, Bool_t set)
	Set or unset the user status bits as specified in f.

virtual void	SetDrawOption (Option_t *option="")
	Set drawing option for object.

virtual void	SetUniqueID (UInt_t uid)
	Set the unique object id.

virtual void	SysError (const char method, const char msgfmt,...) const
	Issue system error message.

R__ALWAYS_INLINE Bool_t	TestBit (UInt_t f) const

Int_t	TestBits (UInt_t f) const

virtual void	UseCurrentStyle ()
	Set current style settings in this object This function is called when either TCanvas::UseCurrentStyle or TROOT::ForceStyle have been invoked.

virtual void	Warning (const char method, const char msgfmt,...) const
	Issue warning message.

virtual Int_t	Write (const char *name=0, Int_t option=0, Int_t bufsize=0)
	Write this object to the current directory.

virtual Int_t	Write (const char *name=0, Int_t option=0, Int_t bufsize=0) const
	Write this object to the current directory.

Protected Member Functions
void	SPlots (Double_t *covmat, Int_t i_excl)
	Computes the sWeights from the covariance matrix.

Protected Member Functions inherited from TObject
virtual void	DoError (int level, const char location, const char fmt, va_list va) const
	Interface to ErrorHandler (protected).

void	MakeZombie ()

Protected Attributes
TMatrixD	fMinmax

Int_t	fNevents

Int_t	fNSpecies

Double_t *	fNumbersOfEvents

Int_t	fNx

Int_t	fNy

TMatrixD	fPdfTot

TString *	fSelection

TMatrixD	fSWeights

TObjArray	fSWeightsHists

TTree *	fTree

TString *	fTreename

TString *	fVarexp

TMatrixD	fXvar

TObjArray	fXvarHists

TMatrixD	fYpdf

TObjArray	fYpdfHists

TMatrixD	fYvar

TObjArray	fYvarHists

Additional Inherited Members
Public Types inherited from TObject
enum	{ kIsOnHeap = 0x01000000 , kNotDeleted = 0x02000000 , kZombie = 0x04000000 , kInconsistent = 0x08000000 , kBitMask = 0x00ffffff }

enum	{ kSingleKey = BIT(0) , kOverwrite = BIT(1) , kWriteDelete = BIT(2) }

enum	EDeprecatedStatusBits { kObjInCanvas = BIT(3) }

enum	EStatusBits { kCanDelete = BIT(0) , kMustCleanup = BIT(3) , kIsReferenced = BIT(4) , kHasUUID = BIT(5) , kCannotPick = BIT(6) , kNoContextMenu = BIT(8) , kInvalidObject = BIT(13) }

Static Public Member Functions inherited from TObject
static Long_t	GetDtorOnly ()
	Return destructor only flag.

static Bool_t	GetObjectStat ()
	Get status of object stat flag.

static void	SetDtorOnly (void *obj)
	Set destructor only flag.

static void	SetObjectStat (Bool_t stat)
	Turn on/off tracking of objects in the TObjectTable.

Protected Types inherited from TObject
enum	{ kOnlyPrepStep = BIT(3) }

#include <TSPlot.h>

Inheritance diagram for TSPlot:

[legend]

Constructor & Destructor Documentation

◆ TSPlot() [1/2]

TSPlot::TSPlot ( )

default constructor (used by I/O only)

Definition at line 296 of file TSPlot.cxx.

◆ TSPlot() [2/2]

TSPlot::TSPlot	(	Int_t	nx,
		Int_t	ny,
		Int_t	ne,
		Int_t	ns,
		TTree *	tree
	)

Normal TSPlot constructor.

nx : number of control variables
ny : number of discriminating variables
ne : total number of events
ns : number of species
tree: input data

Definition at line 317 of file TSPlot.cxx.

◆ ~TSPlot()

TSPlot::~TSPlot ( )

virtual

Destructor.

Definition at line 339 of file TSPlot.cxx.

Member Function Documentation

◆ Browse()

void TSPlot::Browse ( TBrowser * b )

virtual

To browse the histograms.

Reimplemented from TObject.

Definition at line 354 of file TSPlot.cxx.

◆ FillSWeightsHists()

void TSPlot::FillSWeightsHists ( Int_t nbins = 50 )

The order of histograms in the array:

x0_species0, x0_species1,..., x1_species0, x1_species1,..., y0_species0, y0_species1,...

If the histograms have already been filled with a different binning, they are refilled and all histograms are deleted

Definition at line 698 of file TSPlot.cxx.

◆ FillXvarHists()

void TSPlot::FillXvarHists ( Int_t nbins = 100 )

Fills the histograms of x variables (not weighted) with nbins.

Definition at line 528 of file TSPlot.cxx.

◆ FillYpdfHists()

void TSPlot::FillYpdfHists ( Int_t nbins = 100 )

Fills the histograms of pdf-s of y variables with binning nbins.

Definition at line 638 of file TSPlot.cxx.

◆ FillYvarHists()

void TSPlot::FillYvarHists ( Int_t nbins = 100 )

Fill the histograms of y variables.

Definition at line 585 of file TSPlot.cxx.

◆ GetNevents()

Int_t TSPlot::GetNevents ( )

inline

Definition at line 63 of file TSPlot.h.

◆ GetNspecies()

Int_t TSPlot::GetNspecies ( )

inline

Definition at line 64 of file TSPlot.h.

◆ GetSWeights() [1/2]

void TSPlot::GetSWeights ( Double_t * weights )

Returns the matrix of sweights.

It is assumed that the array passed in the argurment is big enough

Definition at line 516 of file TSPlot.cxx.

◆ GetSWeights() [2/2]

void TSPlot::GetSWeights ( TMatrixD & weights )

Returns the matrix of sweights.

Definition at line 505 of file TSPlot.cxx.

◆ GetSWeightsHist()

TH1D * TSPlot::GetSWeightsHist	(	Int_t	ixvar,
		Int_t	ispecies,
		Int_t	iyexcl = `-1`
	)

Returns the histogram of a variable, weighted with sWeights.

If histograms have not been already filled, they are filled with default binning 50
If parameter ixvar!=-1, the histogram of x-variable ixvar is returned for species ispecies
If parameter ixvar==-1, the histogram of y-variable iyexcl is returned for species ispecies
If the histogram has already been filled and the binning is different from the parameter nbins all histograms with old binning will be deleted and refilled.

Definition at line 832 of file TSPlot.cxx.

◆ GetSWeightsHists()

TObjArray * TSPlot::GetSWeightsHists ( )

Returns an array of all histograms of variables, weighted with sWeights.

If histograms have not been already filled, they are filled with default binning 50 The order of histograms in the array:

x0_species0, x0_species1,..., x1_species0, x1_species1,..., y0_species0, y0_species1,...

Definition at line 746 of file TSPlot.cxx.

◆ GetTreeExpression()

TString * TSPlot::GetTreeExpression ( )

inline

Definition at line 78 of file TSPlot.h.

◆ GetTreeName()

TString * TSPlot::GetTreeName ( )

inline

Definition at line 76 of file TSPlot.h.

◆ GetTreeSelection()

TString * TSPlot::GetTreeSelection ( )

inline

Definition at line 77 of file TSPlot.h.

◆ GetXvarHist()

TH1D * TSPlot::GetXvarHist ( Int_t ixvar )

Returns the histogram of variable ixvar.

If histograms have not already been filled, they are filled with default binning 100.

Definition at line 571 of file TSPlot.cxx.

◆ GetXvarHists()

TObjArray * TSPlot::GetXvarHists ( )

Returns the array of histograms of x variables (not weighted).

If histograms have not already been filled, they are filled with default binning 100.

Definition at line 556 of file TSPlot.cxx.

◆ GetYpdfHist()

TH1D * TSPlot::GetYpdfHist	(	Int_t	iyvar,
		Int_t	ispecies
	)

Returns the histogram of the pdf of variable iyvar for species #ispecies, binning nbins.

If histograms have not already been filled, they are filled with default binning 100.

Definition at line 681 of file TSPlot.cxx.

◆ GetYpdfHists()

TObjArray * TSPlot::GetYpdfHists ( )

Returns the array of histograms of pdf's of y variables with binning nbins.

If histograms have not already been filled, they are filled with default binning 100.

Definition at line 667 of file TSPlot.cxx.

◆ GetYvarHist()

TH1D * TSPlot::GetYvarHist ( Int_t iyvar )

Returns the histogram of variable iyvar.If histograms have not already been filled, they are filled with default binning 100.

Definition at line 625 of file TSPlot.cxx.

◆ GetYvarHists()

TObjArray * TSPlot::GetYvarHists ( )

Returns the array of histograms of y variables.

If histograms have not already been filled, they are filled with default binning 100.

Definition at line 611 of file TSPlot.cxx.

◆ IsFolder()

Bool_t TSPlot::IsFolder ( ) const

inlinevirtual

Returns kTRUE in case object contains browsable objects (like containers or lists of other objects).

Reimplemented from TObject.

Definition at line 56 of file TSPlot.h.

◆ MakeSPlot()

void TSPlot::MakeSPlot ( Option_t * option = "v" )

Calculates the sWeights.

The option controls the print level

"Q" - no print out
"V" - prints the estimated #of events in species - default
"VV" - as "V" + the minuit printing + sums of weights for control

Definition at line 404 of file TSPlot.cxx.

◆ RefillHist()

void TSPlot::RefillHist	(	Int_t	type,
		Int_t	nvar,
		Int_t	nbins,
		Double_t	min,
		Double_t	max,
		Int_t	nspecies = `-1`
	)

The Fill...Hist() methods fill the histograms with the real limits on the variables This method allows to refill the specified histogram with user-set boundaries min and max.

Parameters:

type = 1 - histogram of x variable #nvar
type = 2 - histogram of y variable #nvar
type = 3 - histogram of y_pdf for y #nvar and species #nspecies
type = 4 - histogram of x variable #nvar, species #nspecies, WITH sWeights
type = 5 - histogram of y variable #nvar, species #nspecies, WITH sWeights

Definition at line 767 of file TSPlot.cxx.

◆ SetInitialNumbersOfSpecies()

void TSPlot::SetInitialNumbersOfSpecies ( Int_t * numbers )

Set the initial number of events of each species - used as initial estimates in minuit.

Definition at line 388 of file TSPlot.cxx.

◆ SetNEvents()

void TSPlot::SetNEvents ( Int_t ne )

inline

Definition at line 85 of file TSPlot.h.

◆ SetNSpecies()

void TSPlot::SetNSpecies ( Int_t ns )

inline

Definition at line 84 of file TSPlot.h.

◆ SetNX()

void TSPlot::SetNX ( Int_t nx )

inline

Definition at line 82 of file TSPlot.h.

◆ SetNY()

void TSPlot::SetNY ( Int_t ny )

inline

Definition at line 83 of file TSPlot.h.

◆ SetTree()

void TSPlot::SetTree ( TTree * tree )

Set the input Tree.

Definition at line 850 of file TSPlot.cxx.

◆ SetTreeSelection()

void TSPlot::SetTreeSelection	(	const char *	varexp = `""`,
		const char *	selection = `""`,
		Long64_t	firstentry = `0`
	)

Specifies the variables from the tree to be used for splot.

Variables fNx, fNy, fNSpecies and fNEvents should already be set!

In the 1st parameter it is assumed that first fNx variables are x(control variables), then fNy y variables (discriminating variables), then fNy*fNSpecies ypdf variables (probability distribution functions of discriminating variables for different species). The order of pdfs should be: species0_y0, species0_y1,... species1_y0, species1_y1,...species[fNSpecies-1]_y0... The 2nd parameter allows to make a cut TTree::Draw method description contains more details on specifying expression and selection

Definition at line 868 of file TSPlot.cxx.

◆ SPlots()

void TSPlot::SPlots	(	Double_t *	covmat,
		Int_t	i_excl
	)

protected

Computes the sWeights from the covariance matrix.

Definition at line 484 of file TSPlot.cxx.

Member Data Documentation

◆ fMinmax

TMatrixD TSPlot::fMinmax

protected

Definition at line 27 of file TSPlot.h.

◆ fNevents

Int_t TSPlot::fNevents

protected

Definition at line 44 of file TSPlot.h.

◆ fNSpecies

Int_t TSPlot::fNSpecies

protected

Definition at line 43 of file TSPlot.h.

◆ fNumbersOfEvents

Double_t* TSPlot::fNumbersOfEvents

protected

Definition at line 46 of file TSPlot.h.

◆ fNx

Int_t TSPlot::fNx

protected

Definition at line 41 of file TSPlot.h.

◆ fNy

Int_t TSPlot::fNy

protected

Definition at line 42 of file TSPlot.h.

◆ fPdfTot

TMatrixD TSPlot::fPdfTot

protected

Definition at line 26 of file TSPlot.h.

◆ fSelection

TString* TSPlot::fSelection

protected

Definition at line 38 of file TSPlot.h.

◆ fSWeights

TMatrixD TSPlot::fSWeights

protected

Definition at line 28 of file TSPlot.h.

◆ fSWeightsHists

TObjArray TSPlot::fSWeightsHists

protected

Definition at line 33 of file TSPlot.h.

◆ fTree

TTree* TSPlot::fTree

protected

Definition at line 35 of file TSPlot.h.

◆ fTreename

TString* TSPlot::fTreename

protected

Definition at line 36 of file TSPlot.h.

◆ fVarexp

TString* TSPlot::fVarexp

protected

Definition at line 37 of file TSPlot.h.

◆ fXvar

TMatrixD TSPlot::fXvar

protected

Definition at line 23 of file TSPlot.h.

◆ fXvarHists

TObjArray TSPlot::fXvarHists

protected

Definition at line 30 of file TSPlot.h.

◆ fYpdf

TMatrixD TSPlot::fYpdf

protected

Definition at line 25 of file TSPlot.h.

◆ fYpdfHists

TObjArray TSPlot::fYpdfHists

protected

Definition at line 32 of file TSPlot.h.

◆ fYvar

TMatrixD TSPlot::fYvar

protected

Definition at line 24 of file TSPlot.h.

◆ fYvarHists

TObjArray TSPlot::fYvarHists

protected

Definition at line 31 of file TSPlot.h.

Libraries for TSPlot:

[legend]

The documentation for this class was generated from the following files:

math/splot/inc/TSPlot.h
math/splot/src/TSPlot.cxx

The method

Some properties and checks

Different steps followed by TSPlot

Illustrations

Figure 1:

Figure 2:

Figure 3:

Figure 4:

Public Member Functions

Protected Member Functions

Protected Attributes

Additional Inherited Members

Constructor & Destructor Documentation

◆ TSPlot() [1/2]

◆ TSPlot() [2/2]

◆ ~TSPlot()

Member Function Documentation

◆ Browse()

◆ FillSWeightsHists()

◆ FillXvarHists()

◆ FillYpdfHists()

◆ FillYvarHists()

◆ GetNevents()

◆ GetNspecies()

◆ GetSWeights() [1/2]

◆ GetSWeights() [2/2]

◆ GetSWeightsHist()

◆ GetSWeightsHists()

◆ GetTreeExpression()

◆ GetTreeName()

◆ GetTreeSelection()

◆ GetXvarHist()

◆ GetXvarHists()

◆ GetYpdfHist()

◆ GetYpdfHists()

◆ GetYvarHist()

◆ GetYvarHists()

◆ IsFolder()

◆ MakeSPlot()

◆ RefillHist()

◆ SetInitialNumbersOfSpecies()

◆ SetNEvents()

◆ SetNSpecies()

◆ SetNX()

◆ SetNY()

◆ SetTree()

◆ SetTreeSelection()

◆ SPlots()

Member Data Documentation

◆ fMinmax

◆ fNevents

◆ fNSpecies

◆ fNumbersOfEvents

◆ fNx

◆ fNy

◆ fPdfTot

◆ fSelection

◆ fSWeights

◆ fSWeightsHists

◆ fTree

◆ fTreename

◆ fVarexp

◆ fXvar

◆ fXvarHists

◆ fYpdf

◆ fYpdfHists

◆ fYvar

◆ fYvarHists