This class calculates the Kelvin functions Ber(x), Bei(x), Ker(x), Kei(x), and their first derivatives.
Definition at line 38 of file KelvinFunctions.h.
Public Member Functions | |
| virtual | ~KelvinFunctions () |
Static Public Member Functions | |
| static double | Bei (double x) |
| static double | Ber (double x) |
| static double | DBei (double x) |
| Calculates the first derivative of Bei(x). | |
| static double | DBer (double x) |
| Calculates the first derivative of Ber(x). | |
| static double | DKei (double x) |
| Calculates the first derivative of Kei(x). | |
| static double | DKer (double x) |
| Calculates the first derivative of Ker(x). | |
| static double | F1 (double x) |
| Utility function appearing in the calculations of the Kelvin functions Bei(x) and Ber(x) (and their derivatives). | |
| static double | F2 (double x) |
| Utility function appearing in the calculations of the Kelvin functions Kei(x) and Ker(x) (and their derivatives). | |
| static double | G1 (double x) |
| Utility function appearing in the calculations of the Kelvin functions Bei(x) and Ber(x) (and their derivatives). | |
| static double | G2 (double x) |
| Utility function appearing in the calculations of the Kelvin functions Kei(x) and Ker(x) (and their derivatives). | |
| static double | Kei (double x) |
| static double | Ker (double x) |
| static double | M (double x) |
| Utility function appearing in the asymptotic expansions of DBer(x) and DBei(x). | |
| static double | N (double x) |
| Utility function appearing in the asymptotic expansions of DKer(x) and DKei(x). | |
| static double | Phi (double x) |
| Utility function appearing in the asymptotic expansions of DKer(x) and DKei(x). | |
| static double | Theta (double x) |
| Utility function appearing in the asymptotic expansions of DBer(x) and DBei(x). | |
Static Protected Attributes | |
| static double | fgEpsilon = 1.e-20 |
| static double | fgMin = 20 |
#include <Math/KelvinFunctions.h>
|
inlinevirtual |
Definition at line 63 of file KelvinFunctions.h.
\[ Bei(x) = Bei_{0}(x) = Im\left[J_{0}\left(x e^{3\pi i/4}\right)\right] \]
where x is real, and \(J_{0}(z)\) is the zeroth-order Bessel function of the first kind.
If x < fgMin (=20), Bei(x) is computed according to its polynomial approximation
\[ Bei(x) = \sum_{n \geq 0}\frac{(-1)^{n}(x/2)^{4n+2}}{[(2n+1)!]^{2}} \]
For x > fgMin, Bei(x) is computed according to its asymptotic expansion:
\[ Bei(x) = \frac{e^{x/\sqrt{2}}}{\sqrt{2\pi x}} [F1(x) sin\alpha + G1(x) cos\alpha] - \frac{1}{\pi}Ker(x) \]
where \(\alpha = \frac{x}{\sqrt{2}} - \frac{\pi}{8}\).

Definition at line 130 of file KelvinFunctions.cxx.
\[ Ber(x) = Ber_{0}(x) = Re\left[J_{0}\left(x e^{3\pi i/4}\right)\right] \]
where x is real, and \(J_{0}(z)\) is the zeroth-order Bessel function of the first kind.
If x < fgMin (=20), Ber(x) is computed according to its polynomial approximation
\[ Ber(x) = 1 + \sum_{n \geq 1}\frac{(-1)^{n}(x/2)^{4n}}{[(2n)!]^{2}} \]
For x > fgMin, Ber(x) is computed according to its asymptotic expansion:
\[ Ber(x) = \frac{e^{x/\sqrt{2}}}{\sqrt{2\pi x}} [F1(x) cos\alpha + G1(x) sin\alpha] - \frac{1}{\pi}Kei(x) \]
where \(\alpha = \frac{x}{\sqrt{2}} - \frac{\pi}{8}\).
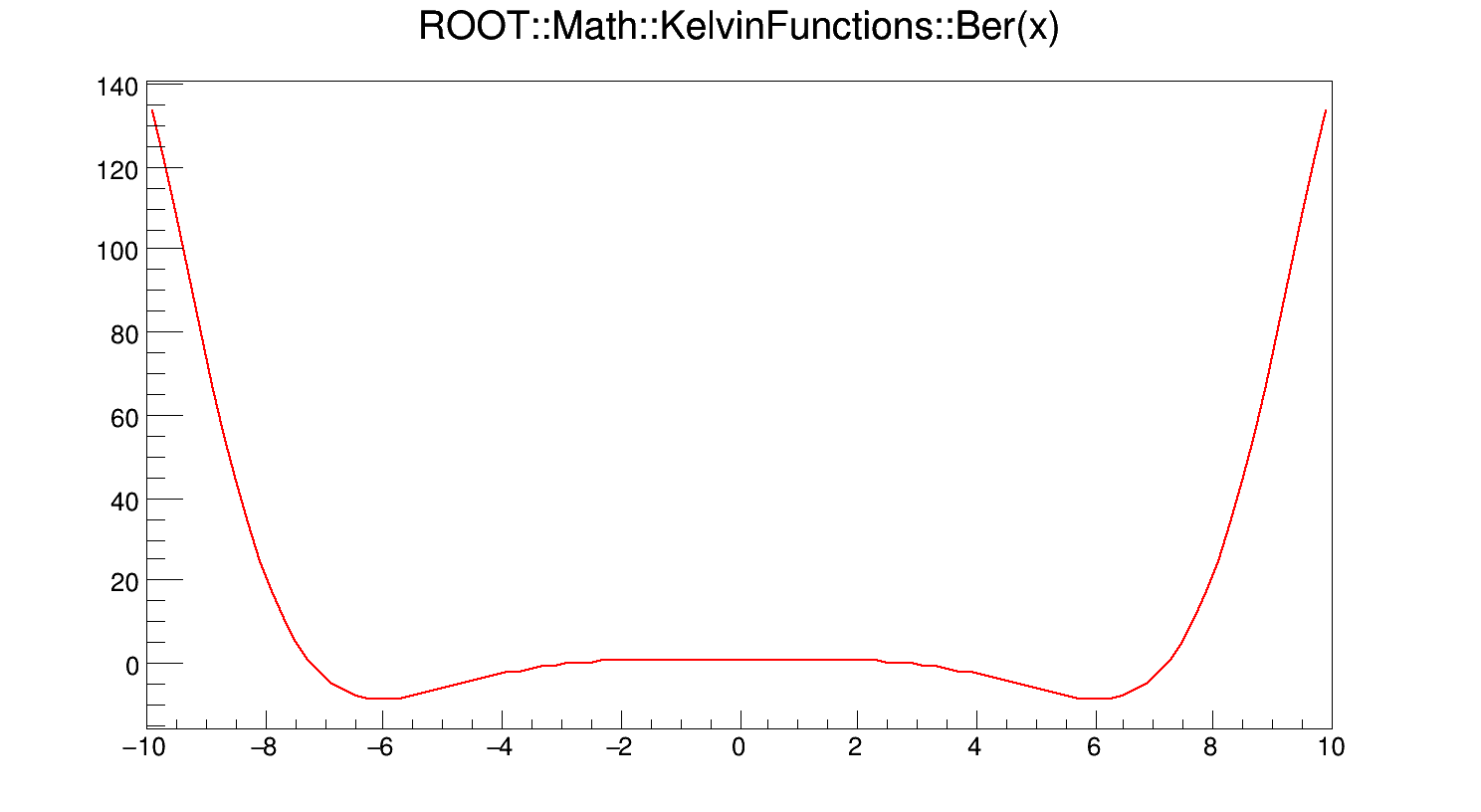
Definition at line 72 of file KelvinFunctions.cxx.
Calculates the first derivative of Bei(x).
If x < fgMin (=20), DBei(x) is computed according to the derivative of the polynomial approximation of Bei(x). Otherwise it is computed according to its asymptotic expansion
\[ \frac{d}{dx} Bei(x) = M sin\left(\theta - \frac{\pi}{4}\right) \]
See also M() and Theta().

Definition at line 359 of file KelvinFunctions.cxx.
Calculates the first derivative of Ber(x).
If x < fgMin (=20), DBer(x) is computed according to the derivative of the polynomial approximation of Ber(x). Otherwise it is computed according to its asymptotic expansion
\[ \frac{d}{dx} Ber(x) = M cos\left(\theta - \frac{\pi}{4}\right) \]
See also M() and Theta().
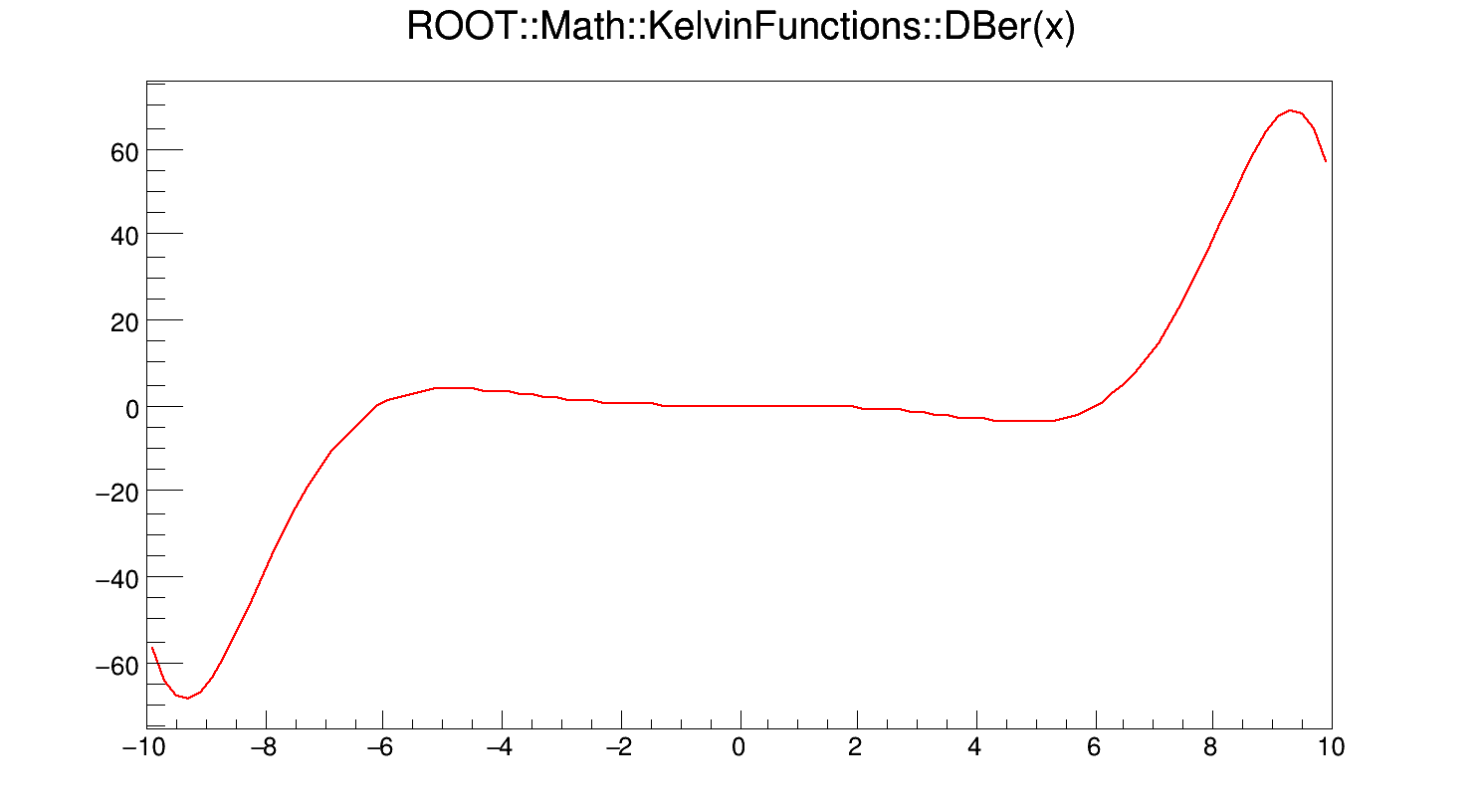
Definition at line 314 of file KelvinFunctions.cxx.
Calculates the first derivative of Kei(x).
If x < fgMin (=20), DKei(x) is computed according to the derivative of the polynomial approximation of Kei(x). Otherwise it is computed according to its asymptotic expansion
\[ \frac{d}{dx} Kei(x) = N sin\left(\phi - \frac{\pi}{4}\right) \]
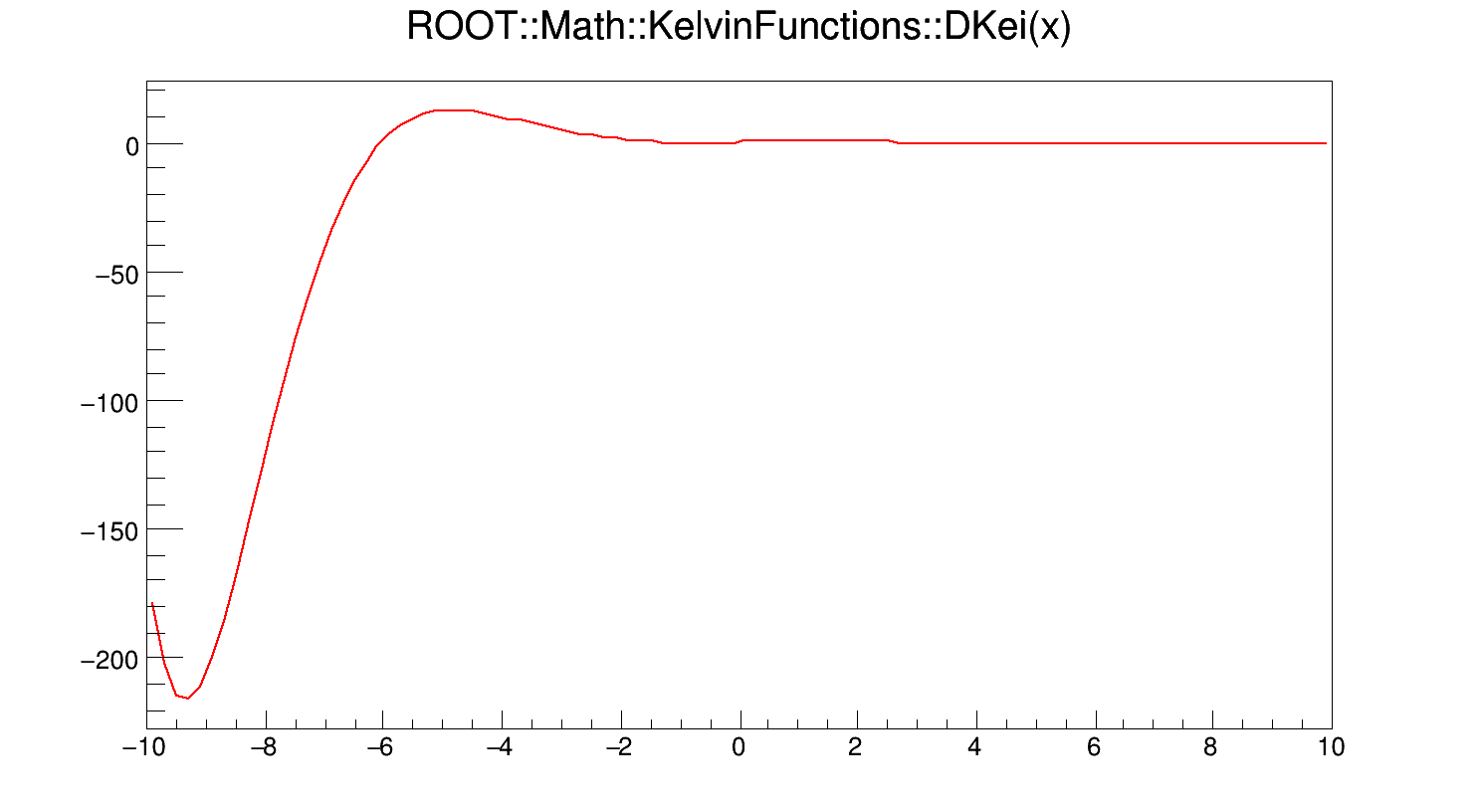
Definition at line 452 of file KelvinFunctions.cxx.
Calculates the first derivative of Ker(x).
If x < fgMin (=20), DKer(x) is computed according to the derivative of the polynomial approximation of Ker(x). Otherwise it is computed according to its asymptotic expansion
\[ \frac{d}{dx} Ker(x) = N cos\left(\phi - \frac{\pi}{4}\right) \]
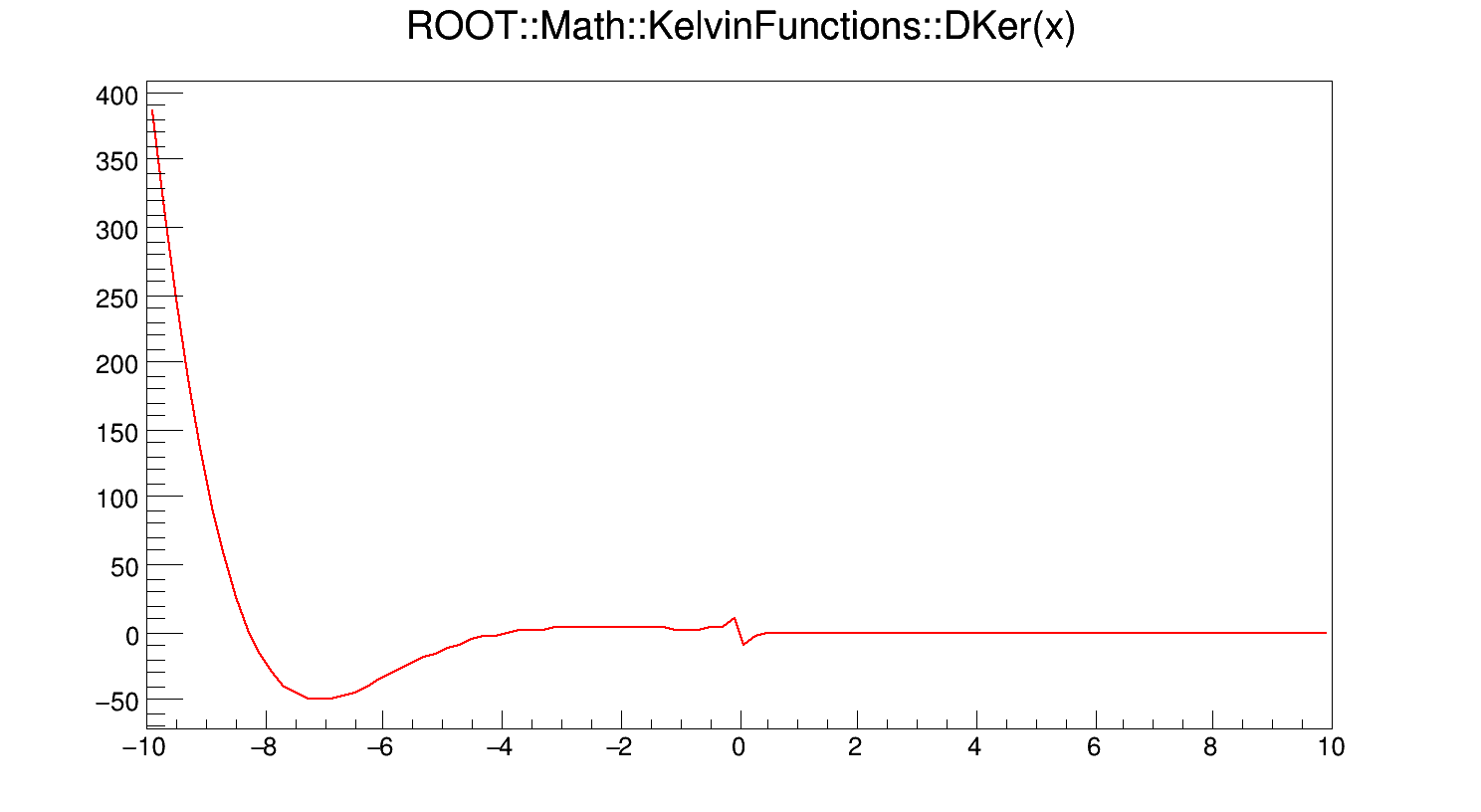
Definition at line 404 of file KelvinFunctions.cxx.
Utility function appearing in the calculations of the Kelvin functions Bei(x) and Ber(x) (and their derivatives).
F1(x) is given by
\[ F1(x) = 1 + \sum_{n \geq 1} \frac{\prod_{m=1}^{n}(2m - 1)^{2}}{n! (8x)^{n}} cos\left(\frac{n\pi}{4}\right) \]
Definition at line 487 of file KelvinFunctions.cxx.
Utility function appearing in the calculations of the Kelvin functions Kei(x) and Ker(x) (and their derivatives).
F2(x) is given by
\[ F2(x) = 1 + \sum_{n \geq 1} (-1)^{n} \frac{\prod_{m=1}^{n}(2m - 1)^{2}}{n! (8x)^{n}} cos\left(\frac{n\pi}{4}\right) \]
Definition at line 516 of file KelvinFunctions.cxx.
Utility function appearing in the calculations of the Kelvin functions Bei(x) and Ber(x) (and their derivatives).
G1(x) is given by
\[ G1(x) = \sum_{n \geq 1} \frac{\prod_{m=1}^{n}(2m - 1)^{2}}{n! (8x)^{n}} sin\left(\frac{n\pi}{4}\right) \]
Definition at line 547 of file KelvinFunctions.cxx.
Utility function appearing in the calculations of the Kelvin functions Kei(x) and Ker(x) (and their derivatives).
G2(x) is given by
\[ G2(x) = \sum_{n \geq 1} (-1)^{n} \frac{\prod_{m=1}^{n}(2m - 1)^{2}}{n! (8x)^{n}} sin\left(\frac{n\pi}{4}\right) \]
Definition at line 574 of file KelvinFunctions.cxx.
\[ Kei(x) = Kei_{0}(x) = Im\left[K_{0}\left(x e^{3\pi i/4}\right)\right] \]
where x is real, and \(K_{0}(z)\) is the zeroth-order modified Bessel function of the second kind.
If x < fgMin (=20), Kei(x) is computed according to its polynomial approximation
\[ Kei(x) = -\left(ln \frac{x}{2} + \gamma\right) Bei(x) - \left(\frac{\pi}{4} - \delta\right) Ber(x) + \sum_{n \geq 0} \frac{(-1)^{n}}{[(2n)!]^{2}} H_{2n} \left(\frac{x}{2}\right)^{4n+2} \]
where \(\gamma = 0.577215664...\) is the Euler-Mascheroni constant, \(\delta = \pi\) for x < 0 and is otherwise zero, and
\[ H_{n} = \sum_{k = 1}^{n} \frac{1}{k} \]
For x > fgMin, Kei(x) is computed according to its asymptotic expansion:
\[ Kei(x) = - \sqrt{\frac{\pi}{2x}} e^{-x/\sqrt{2}} [F2(x) sin\beta + G2(x) cos\beta] \]
where \(\beta = \frac{x}{\sqrt{2}} + \frac{\pi}{8}\).
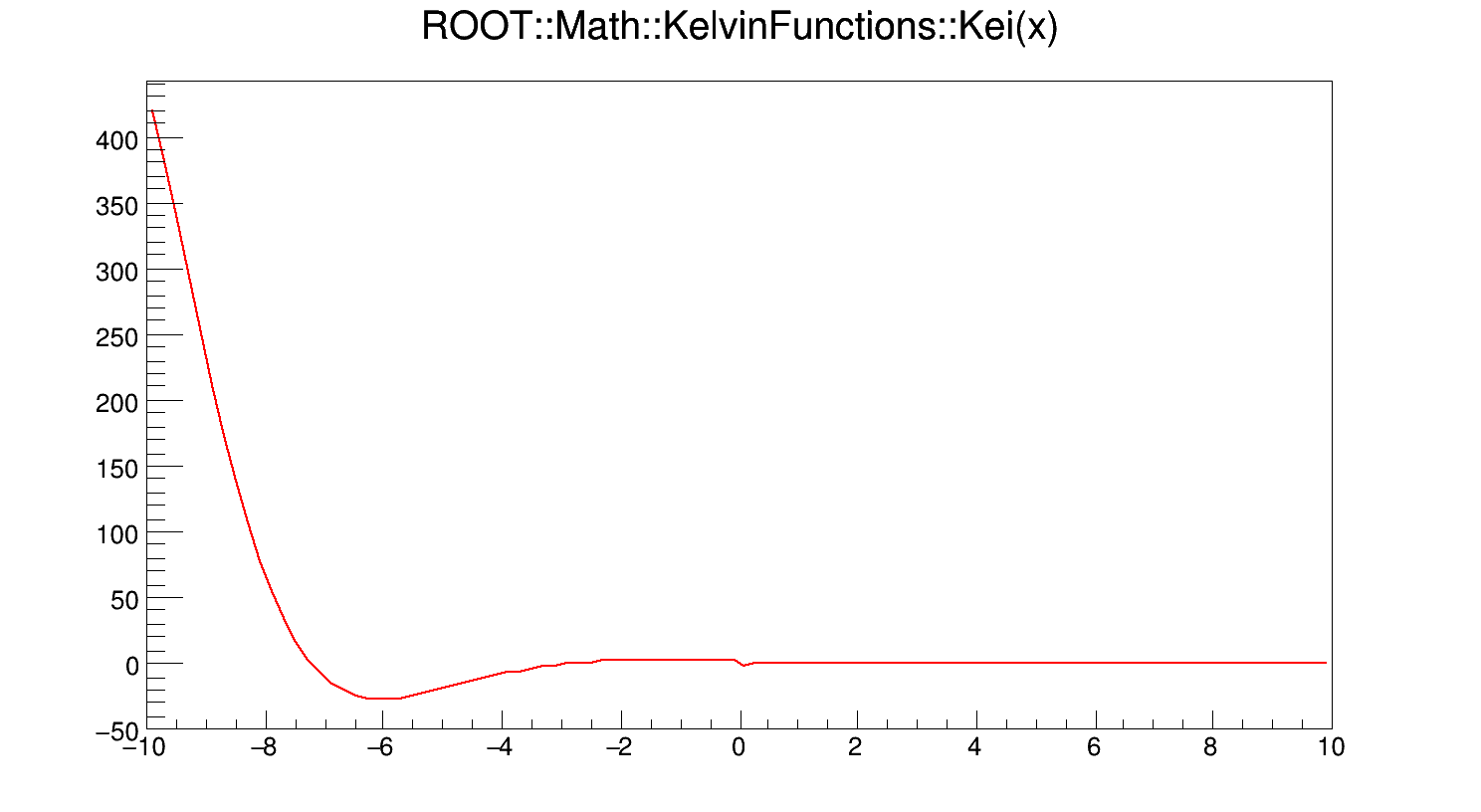
Definition at line 262 of file KelvinFunctions.cxx.
\[ Ker(x) = Ker_{0}(x) = Re\left[K_{0}\left(x e^{3\pi i/4}\right)\right] \]
where x is real, and \(K_{0}(z)\) is the zeroth-order modified Bessel function of the second kind.
If x < fgMin (=20), Ker(x) is computed according to its polynomial approximation
\[ Ker(x) = -\left(ln \frac{|x|}{2} + \gamma\right) Ber(x) + \left(\frac{\pi}{4} - \delta\right) Bei(x) + \sum_{n \geq 0} \frac{(-1)^{n}}{[(2n)!]^{2}} H_{2n} \left(\frac{x}{2}\right)^{4n} \]
where \(\gamma = 0.577215664...\) is the Euler-Mascheroni constant, \(\delta = \pi\) for x < 0 and is otherwise zero, and
\[ H_{n} = \sum_{k = 1}^{n} \frac{1}{k} \]
For x > fgMin, Ker(x) is computed according to its asymptotic expansion:
\[ Ker(x) = \sqrt{\frac{\pi}{2x}} e^{-x/\sqrt{2}} [F2(x) cos\beta + G2(x) sin\beta] \]
where \(\beta = \frac{x}{\sqrt{2}} + \frac{\pi}{8}\).
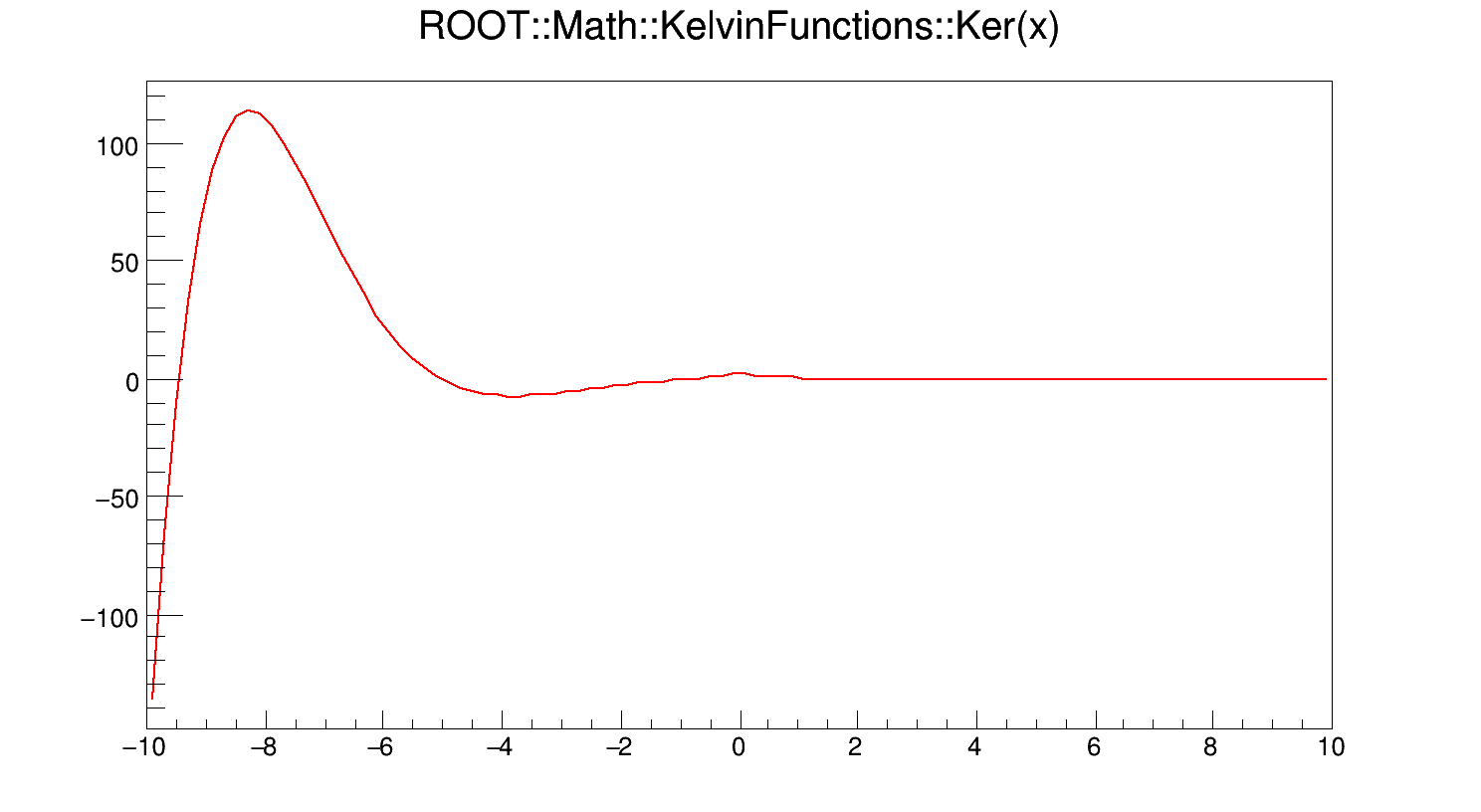
Definition at line 195 of file KelvinFunctions.cxx.
Utility function appearing in the asymptotic expansions of DBer(x) and DBei(x).
M(x) is given by
\[ M(x) = \frac{e^{x/\sqrt{2}}}{\sqrt{2\pi x}}\left(1 + \frac{1}{8\sqrt{2} x} + \frac{1}{256 x^{2}} - \frac{399}{6144\sqrt{2} x^{3}} + O\left(\frac{1}{x^{4}}\right)\right) \]
Definition at line 603 of file KelvinFunctions.cxx.
Utility function appearing in the asymptotic expansions of DKer(x) and DKei(x).
N(x) is given by
\[ N(x) = \sqrt{\frac{\pi}{2x}} e^{-x/\sqrt{2}} \left(1 - \frac{1}{8\sqrt{2} x} + \frac{1}{256 x^{2}} + \frac{399}{6144\sqrt{2} x^{3}} + O\left(\frac{1}{x^{4}}\right)\right) \]
Definition at line 635 of file KelvinFunctions.cxx.
Utility function appearing in the asymptotic expansions of DKer(x) and DKei(x).
\(\phi(x)\) is given by
\[ \phi(x) = - \frac{x}{\sqrt{2}} - \frac{\pi}{8} + \frac{1}{8\sqrt{2} x} - \frac{1}{16 x^{2}} + \frac{25}{384\sqrt{2} x^{3}} + O\left(\frac{1}{x^{5}}\right) \]
Definition at line 651 of file KelvinFunctions.cxx.
Utility function appearing in the asymptotic expansions of DBer(x) and DBei(x).
\(\theta(x)\) is given by
\[ \theta(x) = \frac{x}{\sqrt{2}} - \frac{\pi}{8} - \frac{1}{8\sqrt{2} x} - \frac{1}{16 x^{2}} - \frac{25}{384\sqrt{2} x^{3}} + O\left(\frac{1}{x^{5}}\right) \]
Definition at line 619 of file KelvinFunctions.cxx.
Definition at line 68 of file KelvinFunctions.h.
|
staticprotected |
Definition at line 67 of file KelvinFunctions.h.