Logo ROOT  

Reference Guide
testUnfold7c.C File Reference
Tutorials » TUnfold tutorials

Detailed Description

View in nbviewer Open in SWAN Test program for the classes TUnfoldDensity and TUnfoldBinning.

A toy test of the TUnfold package

This example is documented in conference proceedings:

arXiv:1611.01927 12th Conference on Quark Confinement and the Hadron Spectrum (Confinement XII)

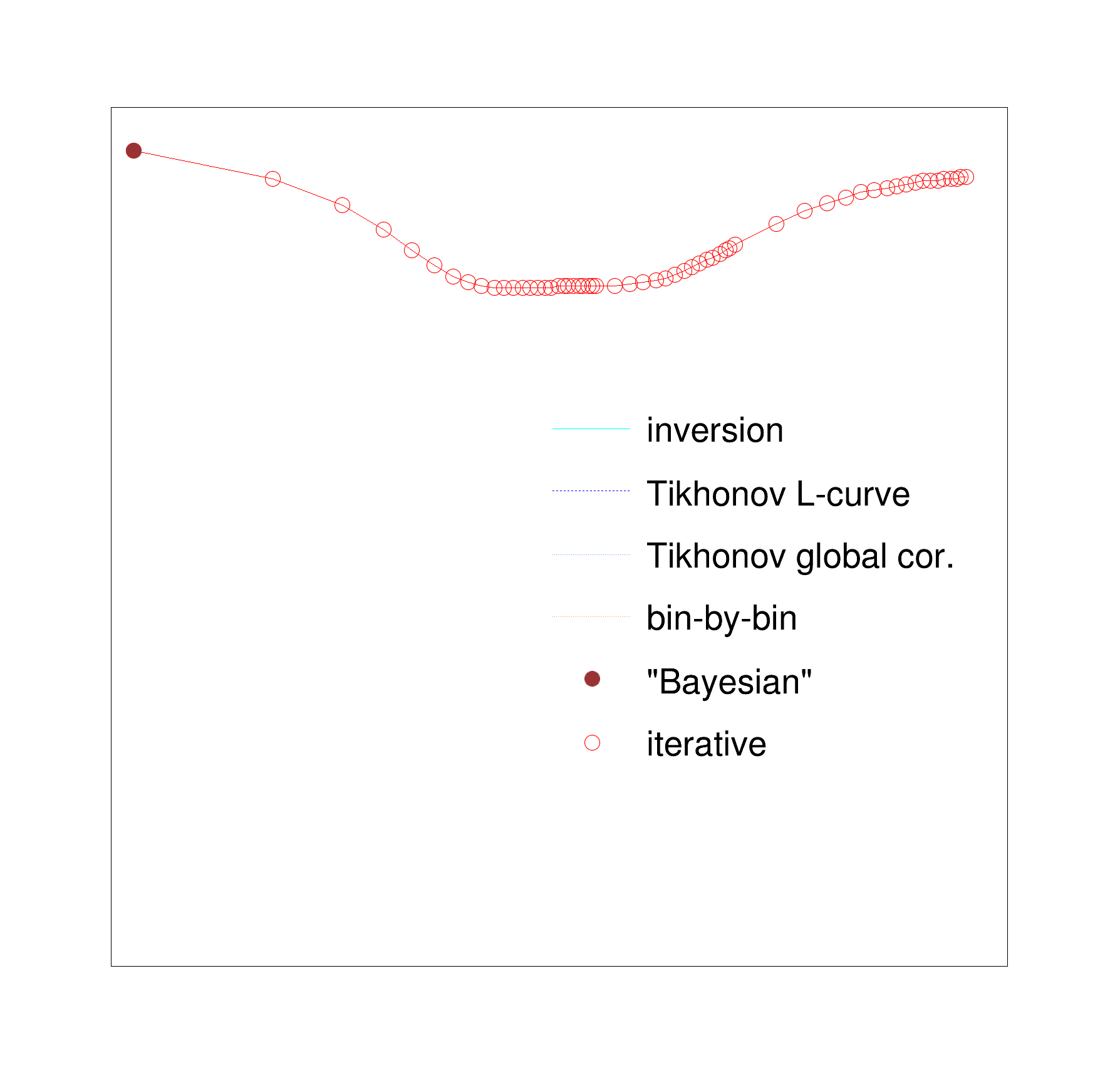
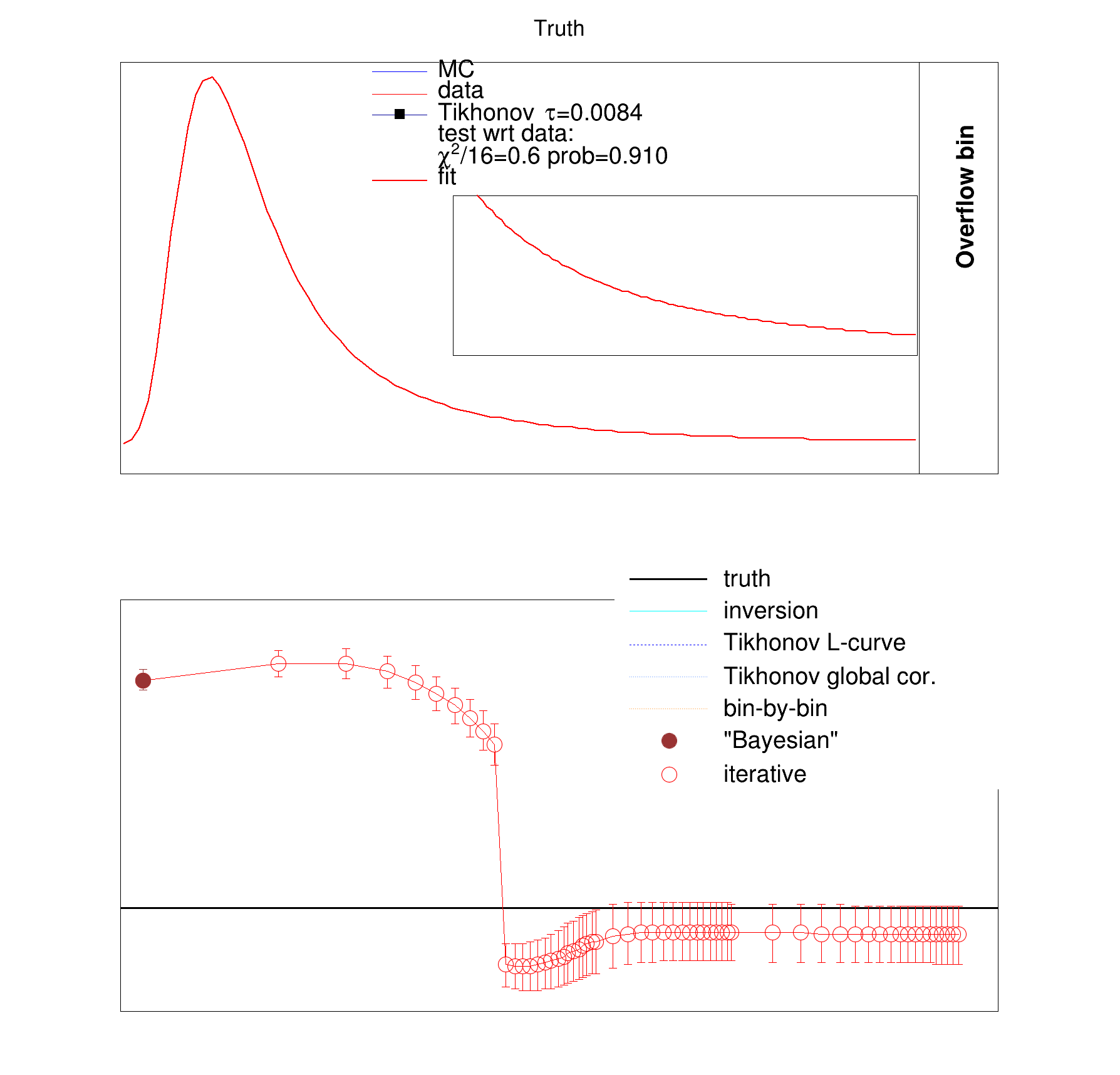
This is an example of unfolding a one-dimensional distribution. It compares various unfolding methods: 

      matrix inversion, template fit, L-curve scan,
      iterative unfolding, etc

Further details can be found in talk by S.Schmitt at:

XII Quark Confinement and the Hadron Spectrum 29.8. - 3.9.2016 Thessaloniki, Greece statictics session (+proceedings)

The example comprises several macros

  • testUnfold7a.C create root files with TTree objects for signal, background and data
    • write files testUnfold7_signal.root testUnfold7_background.root testUnfold7_data.root
  • testUnfold7b.C loop over trees and fill histograms based on the TUnfoldBinning objects
    • read testUnfold7binning.xml testUnfold7_signal.root testUnfold7_background.root testUnfold7_data.root
    • write testUnfold7_histograms.root
  • testUnfold7c.C run the unfolding
    • read testUnfold7_histograms.root
    • write testUnfold7_result.root
    • write many histograms, to compare various unfolding methods
maximum number of iterations: 1000
0
100
200
300
400
500
600
700
800
900
1000
histOutputCtau0_binwU
FCN=8.93341 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 246 TOTAL
EDM=5.88874e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.31303e+03 8.14586e+01 -6.46558e-01 -6.37069e-07
2 p1 6.07588e+00 8.43187e-02 8.29300e-05 6.05555e-04
3 p2 1.76119e+00 6.22596e-02 6.22596e-02 -1.65640e-02
fcn flag=0: npar=3 gin=0 par=[ 2313.03 6.07588 1.76119]
histOutputFtau0_binwU
FCN=8.33089 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 256 TOTAL
EDM=1.30164e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.29259e+03 7.71770e+01 -5.87690e-01 -5.60300e-07
2 p1 6.06670e+00 8.21739e-02 9.54356e-05 4.94678e-04
3 p2 1.77123e+00 5.99548e-02 5.99548e-02 -1.82622e-02
fcn flag=0: npar=3 gin=0 par=[ 2292.59 6.0667 1.77123]
histOutputFAtau0_binwU
FCN=8.36913 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 245 TOTAL
EDM=8.32595e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.30096e+03 7.70512e+01 -5.84335e-01 -5.55161e-07
2 p1 6.06894e+00 8.18042e-02 9.61863e-05 4.98081e-04
3 p2 1.77403e+00 5.97101e-02 5.97101e-02 -1.63881e-02
fcn flag=0: npar=3 gin=0 par=[ 2300.96 6.06894 1.77403]
histOutputFALCurve_binwU
FCN=22.1459 FROM MINOS STATUS=SUCCESSFUL 41 CALLS 245 TOTAL
EDM=9.45435e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.17569e+03 6.33586e+01 -7.58127e-01 -7.69952e-07
2 p1 6.01392e+00 8.30555e-02 4.08832e-04 3.30679e-04
3 p2 1.88219e+00 5.23609e-02 5.23609e-02 5.06081e-03
fcn flag=0: npar=3 gin=0 par=[ 2175.69 6.01392 1.88219]
histOutputFArho_binwU
FCN=36.4398 FROM MINOS STATUS=SUCCESSFUL 40 CALLS 232 TOTAL
EDM=2.77325e-10 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.08861e+03 5.43343e+01 -6.34044e-01 1.59227e-05
2 p1 5.94794e+00 8.13038e-02 6.74321e-04 5.84058e-03
3 p2 1.96595e+00 4.70282e-02 4.70282e-02 2.97184e-03
fcn flag=0: npar=3 gin=0 par=[ 2088.61 5.94794 1.96595]
histOutputBBBO
bad global correlation 8 -2.22045e-16
FCN=19.0585 FROM MINOS STATUS=SUCCESSFUL 41 CALLS 246 TOTAL
EDM=2.03654e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 1.96305e+03 5.15629e+01 -3.43591e-01 -2.42531e-06
2 p1 5.90214e+00 8.16734e-02 3.93909e-04 -2.16048e-03
3 p2 2.07111e+00 4.60711e-02 4.60711e-02 1.16327e-02
fcn flag=0: npar=3 gin=0 par=[ 1963.05 5.90214 2.07111]
histOutputAgorep0
FCN=197.953 FROM MINOS STATUS=SUCCESSFUL 40 CALLS 210 TOTAL
EDM=9.26891e-10 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 1.70700e+03 3.06275e+01 -2.31409e-01 -7.75689e-05
2 p1 5.62399e+00 5.32143e-02 5.86793e-04 1.62278e-01
3 p2 2.24364e+00 2.01553e-02 2.01553e-02 -9.80592e-02
fcn flag=0: npar=3 gin=0 par=[ 1707 5.62399 2.24364]
histOutputAgorep1
FCN=118.197 FROM MINOS STATUS=SUCCESSFUL 41 CALLS 245 TOTAL
EDM=1.41288e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 1.76667e+03 3.39695e+01 -2.00491e-01 4.55847e-06
2 p1 5.81350e+00 6.99472e-02 6.49043e-04 -1.07893e-03
3 p2 2.27527e+00 2.62131e-02 2.62131e-02 4.62837e-02
fcn flag=0: npar=3 gin=0 par=[ 1766.67 5.8135 2.27527]
histOutputAgorep2
FCN=103.621 FROM MINOS STATUS=SUCCESSFUL 41 CALLS 226 TOTAL
EDM=3.48457e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 1.79420e+03 3.50632e+01 -2.07985e-01 1.87878e-05
2 p1 5.89902e+00 7.71591e-02 7.24696e-04 -5.64614e-03
3 p2 2.27417e+00 2.89737e-02 2.89737e-02 1.08644e-02
fcn flag=0: npar=3 gin=0 par=[ 1794.2 5.89902 2.27417]
histOutputAgorep3
FCN=96.8081 FROM MINOS STATUS=SUCCESSFUL 40 CALLS 230 TOTAL
EDM=1.01374e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 1.81622e+03 3.59127e+01 -2.11966e-01 2.58262e-05
2 p1 5.93725e+00 8.05303e-02 7.79780e-04 -6.05489e-03
3 p2 2.25891e+00 3.05064e-02 3.05064e-02 -3.33267e-03
fcn flag=0: npar=3 gin=0 par=[ 1816.22 5.93725 2.25891]
histOutputAgorep4
FCN=91.6257 FROM MINOS STATUS=SUCCESSFUL 40 CALLS 226 TOTAL
EDM=1.0176e-06 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 1.83674e+03 3.67459e+01 -2.50605e-01 3.52881e-05
2 p1 5.95680e+00 8.23367e-02 8.23874e-04 -9.09042e-03
3 p2 2.23850e+00 3.16079e-02 3.16079e-02 -3.58208e-03
fcn flag=0: npar=3 gin=0 par=[ 1836.74 5.9568 2.2385]
histOutputAgorep5
FCN=86.8941 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 247 TOTAL
EDM=1.04021e-06 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 1.85665e+03 3.76381e+01 -2.52279e-01 1.57236e-05
2 p1 5.96958e+00 8.35183e-02 7.58226e-04 4.81052e-03
3 p2 2.21640e+00 3.26294e-02 3.26294e-02 -1.75257e-03
fcn flag=0: npar=3 gin=0 par=[ 1856.65 5.96958 2.2164]
histOutputAgorep6
FCN=82.3357 FROM MINOS STATUS=SUCCESSFUL 41 CALLS 224 TOTAL
EDM=6.44618e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 1.87657e+03 3.86709e+01 -2.78125e-01 -2.56340e-06
2 p1 5.98002e+00 8.44752e-02 7.10909e-04 -3.51034e-04
3 p2 2.19350e+00 3.37655e-02 3.37655e-02 -2.33096e-03
fcn flag=0: npar=3 gin=0 par=[ 1876.57 5.98002 2.1935]
histOutputAgorep7
FCN=77.8736 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 225 TOTAL
EDM=4.37712e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 1.89690e+03 3.99390e+01 -2.11725e-01 1.85322e-05
2 p1 5.99052e+00 8.54687e-02 4.45266e-04 5.96412e-04
3 p2 2.16994e+00 3.52059e-02 3.52059e-02 -2.35106e-03
fcn flag=0: npar=3 gin=0 par=[ 1896.9 5.99052 2.16994]
histOutputAgorep8
FCN=73.4731 FROM MINOS STATUS=SUCCESSFUL 22 CALLS 209 TOTAL
EDM=1.45352e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 1.91835e+03 4.16429e+01 4.70965e-03 -3.27989e-05
2 p1 6.00210e+00 8.67252e-02 5.03664e-03 -7.95229e-03
3 p2 2.14524e+00 3.72357e-02 3.72357e-02 -2.98314e-03
fcn flag=0: npar=3 gin=0 par=[ 1918.35 6.0021 2.14524]
histOutputAgorep9
FCN=69.0987 FROM MINOS STATUS=SUCCESSFUL 43 CALLS 310 TOTAL
EDM=1.05195e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 1.94189e+03 4.42557e+01 7.02507e-01 -5.31740e-07
2 p1 6.01603e+00 8.87020e-02 1.45259e-04 2.52707e-03
3 p2 2.11836e+00 4.05058e-02 4.05058e-02 -4.69699e-03
fcn flag=0: npar=3 gin=0 par=[ 1941.89 6.01603 2.11836]
histOutputAgorep10
FCN=42.5138 FROM MINOS STATUS=SUCCESSFUL 48 CALLS 275 TOTAL
EDM=1.16992e-06 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.38279e+03 6.30886e+01 -1.52362e+00 -3.79195e-06
2 p1 6.23206e+00 7.49655e-02 1.55602e-03 2.08326e-03
3 p2 1.69110e+00 4.10787e-02 4.10787e-02 3.66298e-03
fcn flag=0: npar=3 gin=0 par=[ 2382.79 6.23206 1.6911]
histOutputAgorep11
FCN=38.7947 FROM MINOS STATUS=SUCCESSFUL 53 CALLS 274 TOTAL
EDM=6.33849e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.38925e+03 6.51150e+01 -1.79953e+00 -4.99893e-06
2 p1 6.21773e+00 7.53087e-02 1.68505e-03 2.26309e-03
3 p2 1.68830e+00 4.27987e-02 4.27987e-02 4.15636e-03
fcn flag=0: npar=3 gin=0 par=[ 2389.25 6.21773 1.6883]
histOutputAgorep12
FCN=35.7239 FROM MINOS STATUS=SUCCESSFUL 53 CALLS 256 TOTAL
EDM=1.0756e-06 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.39249e+03 6.71290e+01 -2.02287e+00 -6.02090e-06
2 p1 6.20537e+00 7.56420e-02 1.73603e-03 2.34305e-03
3 p2 1.68766e+00 4.46099e-02 4.46099e-02 3.89585e-03
fcn flag=0: npar=3 gin=0 par=[ 2392.49 6.20537 1.68766]
histOutputAgorep13
FCN=33.1305 FROM MINOS STATUS=SUCCESSFUL 53 CALLS 266 TOTAL
EDM=9.97639e-09 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.39331e+03 6.91286e+01 -2.34259e+00 -7.68653e-06
2 p1 6.19428e+00 7.59739e-02 1.84156e-03 2.43651e-03
3 p2 1.68865e+00 4.64913e-02 4.64913e-02 4.39265e-03
fcn flag=0: npar=3 gin=0 par=[ 2393.31 6.19428 1.68865]
histOutputAgorep14
FCN=30.8966 FROM MINOS STATUS=SUCCESSFUL 53 CALLS 270 TOTAL
EDM=4.6127e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.39211e+03 7.11079e+01 -2.65201e+00 -9.49211e-06
2 p1 6.18428e+00 7.63206e-02 1.90899e-03 2.51019e-03
3 p2 1.69100e+00 4.84299e-02 4.84299e-02 3.28310e-03
fcn flag=0: npar=3 gin=0 par=[ 2392.11 6.18428 1.691]
histOutputAgorep15
FCN=28.9403 FROM MINOS STATUS=SUCCESSFUL 53 CALLS 250 TOTAL
EDM=1.94659e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.38938e+03 7.30612e+01 -2.98063e+00 -1.15946e-05
2 p1 6.17507e+00 7.66907e-02 1.96432e-03 2.54799e-03
3 p2 1.69439e+00 5.04042e-02 5.04042e-02 1.12352e-02
fcn flag=0: npar=3 gin=0 par=[ 2389.38 6.17507 1.69439]
histOutputAgorep16
FCN=27.2043 FROM MINOS STATUS=SUCCESSFUL 53 CALLS 272 TOTAL
EDM=4.01378e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.38553e+03 7.49108e+01 -3.28242e+00 -1.37473e-05
2 p1 6.16650e+00 7.70848e-02 1.98117e-03 2.58762e-03
3 p2 1.69854e+00 5.23430e-02 5.23430e-02 5.77046e-03
fcn flag=0: npar=3 gin=0 par=[ 2385.53 6.1665 1.69854]
histOutputAgorep17
FCN=25.6479 FROM MINOS STATUS=SUCCESSFUL 53 CALLS 271 TOTAL
EDM=1.03284e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.38090e+03 7.66545e+01 -3.56030e+00 -1.58936e-05
2 p1 6.15848e+00 7.75090e-02 1.96997e-03 2.61287e-03
3 p2 1.70322e+00 5.42224e-02 5.42224e-02 1.14047e-04
fcn flag=0: npar=3 gin=0 par=[ 2380.9 6.15848 1.70322]
histOutputAgorep18
FCN=24.2424 FROM MINOS STATUS=SUCCESSFUL 53 CALLS 274 TOTAL
EDM=7.02908e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.37584e+03 7.82241e+01 -3.80188e+00 -1.79158e-05
2 p1 6.15095e+00 7.79564e-02 1.93204e-03 2.64258e-03
3 p2 1.70817e+00 5.59703e-02 5.59703e-02 -1.62661e-03
fcn flag=0: npar=3 gin=0 par=[ 2375.84 6.15095 1.70817]
histOutputAgorep19
FCN=22.9669 FROM MINOS STATUS=SUCCESSFUL 53 CALLS 272 TOTAL
EDM=1.59258e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.37062e+03 7.95695e+01 -3.97077e+00 -1.94404e-05
2 p1 6.14388e+00 7.84164e-02 1.85856e-03 2.66687e-03
3 p2 1.71318e+00 5.75286e-02 5.75286e-02 -8.66092e-03
fcn flag=0: npar=3 gin=0 par=[ 2370.62 6.14388 1.71318]
histOutputAgorep20
FCN=21.8061 FROM MINOS STATUS=SUCCESSFUL 53 CALLS 274 TOTAL
EDM=1.38198e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.36546e+03 8.06561e+01 -4.03758e+00 -2.01300e-05
2 p1 6.13724e+00 7.88745e-02 1.74752e-03 2.66539e-03
3 p2 1.71809e+00 5.88535e-02 5.88535e-02 -7.23212e-03
fcn flag=0: npar=3 gin=0 par=[ 2365.46 6.13724 1.71809]
histOutputAgorep21
FCN=20.7482 FROM MINOS STATUS=SUCCESSFUL 52 CALLS 272 TOTAL
EDM=7.21168e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.36059e+03 8.14579e+01 -4.02733e+00 -2.01393e-05
2 p1 6.13112e+00 7.93155e-02 1.62003e-03 2.63937e-03
3 p2 1.72273e+00 5.99070e-02 5.99070e-02 -5.80001e-03
fcn flag=0: npar=3 gin=0 par=[ 2360.59 6.13112 1.72273]
histOutputAgorep22
FCN=19.7836 FROM MINOS STATUS=SUCCESSFUL 52 CALLS 270 TOTAL
EDM=3.34786e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.35612e+03 8.19821e+01 -3.94347e+00 -1.95259e-05
2 p1 6.12550e+00 7.97251e-02 1.48328e-03 2.59034e-03
3 p2 1.72699e+00 6.06866e-02 6.06866e-02 -4.35463e-03
fcn flag=0: npar=3 gin=0 par=[ 2356.12 6.1255 1.72699]
histOutputAgorep23
FCN=18.9042 FROM MINOS STATUS=SUCCESSFUL 52 CALLS 262 TOTAL
EDM=1.44601e-06 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.35205e+03 8.22630e+01 -3.74775e+00 -1.79879e-05
2 p1 6.12036e+00 8.00948e-02 1.32701e-03 2.47404e-03
3 p2 1.73088e+00 6.12207e-02 6.12207e-02 -9.57795e-02
fcn flag=0: npar=3 gin=0 par=[ 2352.05 6.12036 1.73088]
histOutputAgorep24
FCN=18.1027 FROM MINOS STATUS=SUCCESSFUL 52 CALLS 247 TOTAL
EDM=8.41443e-11 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.34855e+03 8.23594e+01 -3.55870e+00 -1.64478e-05
2 p1 6.11571e+00 8.04170e-02 1.19473e-03 2.29569e-03
3 p2 1.73431e+00 6.15483e-02 6.15483e-02 -9.92034e-02
fcn flag=0: npar=3 gin=0 par=[ 2348.55 6.11571 1.73431]
histOutputAgorep25
FCN=17.3722 FROM MINOS STATUS=SUCCESSFUL 52 CALLS 257 TOTAL
EDM=4.90537e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.34548e+03 8.22580e+01 -3.30881e+00 -1.45975e-05
2 p1 6.11149e+00 8.06925e-02 1.06091e-03 2.09257e-03
3 p2 1.73731e+00 6.16718e-02 6.16718e-02 -8.63281e-02
fcn flag=0: npar=3 gin=0 par=[ 2345.48 6.11149 1.73731]
histOutputAgorep30
FCN=14.582 FROM MINOS STATUS=SUCCESSFUL 50 CALLS 211 TOTAL
EDM=2.08761e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33586e+03 8.07919e+01 -2.21138e+00 -6.18318e-06
2 p1 6.09634e+00 8.15191e-02 6.23337e-04 6.70530e-04
3 p2 1.74717e+00 6.09954e-02 6.09954e-02 -4.47004e-02
fcn flag=0: npar=3 gin=0 par=[ 2335.86 6.09634 1.74717]
histOutputAgorep35
FCN=12.8045 FROM MINOS STATUS=SUCCESSFUL 47 CALLS 208 TOTAL
EDM=1.86803e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33188e+03 7.91862e+01 -1.56545e+00 -3.61044e-06
2 p1 6.08782e+00 8.18280e-02 4.23272e-04 3.37543e-04
3 p2 1.75171e+00 5.97919e-02 5.97919e-02 -2.46281e-02
fcn flag=0: npar=3 gin=0 par=[ 2331.88 6.08782 1.75171]
histOutputAgorep40
FCN=11.6423 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 222 TOTAL
EDM=4.043e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33031e+03 7.80070e+01 -1.19106e+00 -2.37601e-06
2 p1 6.08295e+00 8.19385e-02 4.83146e-04 -5.51574e-04
3 p2 1.75384e+00 5.88122e-02 5.88122e-02 -1.94809e-02
fcn flag=0: npar=3 gin=0 par=[ 2330.31 6.08295 1.75384]
histOutputAgorep45
FCN=10.8611 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 237 TOTAL
EDM=3.9053e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.32976e+03 7.71762e+01 -9.93328e-01 -1.19408e-06
2 p1 6.08016e+00 8.19691e-02 3.71659e-04 2.13641e-04
3 p2 1.75487e+00 5.80859e-02 5.80859e-02 1.04405e-02
fcn flag=0: npar=3 gin=0 par=[ 2329.76 6.08016 1.75487]
histOutputAgorep50
FCN=10.3233 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 247 TOTAL
EDM=8.48175e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.32968e+03 7.66038e+01 -8.74373e-01 -7.97139e-07
2 p1 6.07856e+00 8.19659e-02 3.02199e-04 6.94926e-04
3 p2 1.75534e+00 5.75655e-02 5.75655e-02 3.31828e-03
fcn flag=0: npar=3 gin=0 par=[ 2329.68 6.07856 1.75534]
histOutputAgorep55
FCN=9.94614 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 250 TOTAL
EDM=4.76626e-09 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.32980e+03 7.61955e+01 -8.08168e-01 -7.09334e-07
2 p1 6.07770e+00 8.19469e-02 2.61367e-04 8.45893e-04
3 p2 1.75551e+00 5.71826e-02 5.71826e-02 3.73373e-03
fcn flag=0: npar=3 gin=0 par=[ 2329.8 6.0777 1.75551]
histOutputAgorep60
FCN=9.67782 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 248 TOTAL
EDM=1.54395e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.32999e+03 7.58992e+01 -7.36164e-01 -6.45670e-07
2 p1 6.07728e+00 8.19210e-02 2.23970e-04 8.25729e-04
3 p2 1.75556e+00 5.68981e-02 5.68981e-02 3.71636e-03
fcn flag=0: npar=3 gin=0 par=[ 2329.99 6.07728 1.75556]
histOutputAgorep65
FCN=9.48518 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 249 TOTAL
EDM=1.36646e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33024e+03 7.56796e+01 -7.15953e-01 -6.48531e-07
2 p1 6.07715e+00 8.18924e-02 2.08415e-04 7.53721e-04
3 p2 1.75548e+00 5.66806e-02 5.66806e-02 4.08269e-03
fcn flag=0: npar=3 gin=0 par=[ 2330.24 6.07715 1.75548]
histOutputAgorep70
FCN=9.34625 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 249 TOTAL
EDM=1.48077e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33047e+03 7.55150e+01 -6.87038e-01 -6.21305e-07
2 p1 6.07720e+00 8.18634e-02 1.92180e-04 6.50846e-04
3 p2 1.75538e+00 5.65139e-02 5.65139e-02 4.18782e-03
fcn flag=0: npar=3 gin=0 par=[ 2330.47 6.0772 1.75538]
histOutputAgorep75
FCN=9.24612 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 240 TOTAL
EDM=9.44627e-10 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33070e+03 7.53898e+01 -6.58731e-01 -5.82957e-07
2 p1 6.07736e+00 8.18350e-02 1.77532e-04 5.43417e-04
3 p2 1.75525e+00 5.63839e-02 5.63839e-02 4.18492e-03
fcn flag=0: npar=3 gin=0 par=[ 2330.7 6.07736 1.75525]
histOutputAgorep80
FCN=9.17445 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 251 TOTAL
EDM=4.65618e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33090e+03 7.52935e+01 -6.42479e-01 -5.52498e-07
2 p1 6.07760e+00 8.18081e-02 1.68737e-04 4.49906e-04
3 p2 1.75510e+00 5.62810e-02 5.62810e-02 4.26807e-03
fcn flag=0: npar=3 gin=0 par=[ 2330.9 6.0776 1.7551]
histOutputAgorep85
FCN=9.1239 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 249 TOTAL
EDM=1.18194e-09 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33110e+03 7.52204e+01 -6.28897e-01 -5.23139e-07
2 p1 6.07789e+00 8.17827e-02 1.61491e-04 3.68211e-04
3 p2 1.75495e+00 5.61999e-02 5.61999e-02 4.31248e-03
fcn flag=0: npar=3 gin=0 par=[ 2331.1 6.07789 1.75495]
histOutputAgorep90
FCN=9.0892 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 251 TOTAL
EDM=7.61668e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33128e+03 7.51639e+01 -6.26365e-01 -5.09127e-07
2 p1 6.07819e+00 8.17586e-02 1.57874e-04 3.02556e-04
3 p2 1.75479e+00 5.61345e-02 5.61345e-02 1.03903e-04
fcn flag=0: npar=3 gin=0 par=[ 2331.28 6.07819 1.75479]
histOutputAgorep95
FCN=9.06651 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 239 TOTAL
EDM=1.52214e-06 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33146e+03 7.51221e+01 -6.05868e-01 -4.66139e-07
2 p1 6.07855e+00 8.17366e-02 1.53529e-04 2.49560e-04
3 p2 1.75465e+00 5.60835e-02 5.60835e-02 8.25313e-04
fcn flag=0: npar=3 gin=0 par=[ 2331.46 6.07855 1.75465]
histOutputAgorep100
FCN=9.05295 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 251 TOTAL
EDM=8.44284e-10 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33157e+03 7.50847e+01 -5.97076e-01 -4.43205e-07
2 p1 6.07885e+00 8.17166e-02 1.46496e-04 1.92809e-04
3 p2 1.75450e+00 5.60389e-02 5.60389e-02 -3.06175e-05
fcn flag=0: npar=3 gin=0 par=[ 2331.57 6.07885 1.7545]
histOutputAgorep150
FCN=9.12732 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 255 TOTAL
EDM=6.17566e-10 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33243e+03 7.49926e+01 -5.59551e-01 -3.40570e-07
2 p1 6.08166e+00 8.15855e-02 1.30107e-04 1.08766e-05
3 p2 1.75329e+00 5.58708e-02 5.58708e-02 -8.32624e-05
fcn flag=0: npar=3 gin=0 par=[ 2332.43 6.08166 1.75329]
histOutputAgorep200
FCN=9.27969 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 256 TOTAL
EDM=3.22108e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33280e+03 7.50280e+01 -5.21032e-01 -2.93898e-07
2 p1 6.08337e+00 8.15391e-02 1.17504e-04 6.65865e-06
3 p2 1.75248e+00 5.58512e-02 5.58512e-02 4.23885e-03
fcn flag=0: npar=3 gin=0 par=[ 2332.8 6.08337 1.75248]
histOutputAgorep250
FCN=9.41695 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 256 TOTAL
EDM=4.48432e-08 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33307e+03 7.50763e+01 -5.32075e-01 -3.19342e-07
2 p1 6.08433e+00 8.15355e-02 1.22201e-04 4.26469e-05
3 p2 1.75185e+00 5.58558e-02 5.58558e-02 -4.08448e-05
fcn flag=0: npar=3 gin=0 par=[ 2333.07 6.08433 1.75185]
histOutputAgorep300
FCN=9.53327 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 256 TOTAL
EDM=1.37538e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33325e+03 7.51176e+01 -5.22404e-01 -3.18989e-07
2 p1 6.08484e+00 8.15543e-02 1.19684e-04 7.24853e-05
3 p2 1.75138e+00 5.58643e-02 5.58643e-02 -4.50409e-05
fcn flag=0: npar=3 gin=0 par=[ 2333.25 6.08484 1.75138]
histOutputAgorep350
FCN=9.63207 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 256 TOTAL
EDM=2.95594e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33338e+03 7.51506e+01 -5.12638e-01 -3.16214e-07
2 p1 6.08509e+00 8.15835e-02 1.16882e-04 9.52549e-05
3 p2 1.75103e+00 5.58718e-02 5.58718e-02 -5.96976e-05
fcn flag=0: npar=3 gin=0 par=[ 2333.38 6.08509 1.75103]
histOutputAgorep400
FCN=9.71683 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 255 TOTAL
EDM=4.73926e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33348e+03 7.51776e+01 -5.05857e-01 -3.15695e-07
2 p1 6.08518e+00 8.16165e-02 1.14962e-04 1.14840e-04
3 p2 1.75075e+00 5.58792e-02 5.58792e-02 4.43672e-03
fcn flag=0: npar=3 gin=0 par=[ 2333.48 6.08518 1.75075]
histOutputAgorep450
FCN=9.7902 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 255 TOTAL
EDM=6.26571e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33355e+03 7.51980e+01 -4.99799e-01 -3.14159e-07
2 p1 6.08518e+00 8.16490e-02 1.13118e-04 1.29000e-04
3 p2 1.75054e+00 5.58845e-02 5.58845e-02 4.37898e-03
fcn flag=0: npar=3 gin=0 par=[ 2333.55 6.08518 1.75054]
histOutputAgorep500
FCN=9.85409 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 255 TOTAL
EDM=7.27784e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33359e+03 7.52138e+01 -4.95492e-01 -3.13014e-07
2 p1 6.08512e+00 8.16791e-02 1.11706e-04 1.38622e-04
3 p2 1.75037e+00 5.58888e-02 5.58888e-02 4.35406e-03
fcn flag=0: npar=3 gin=0 par=[ 2333.59 6.08512 1.75037]
histOutputAgorep550
FCN=9.90995 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 255 TOTAL
EDM=7.72436e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33362e+03 7.52268e+01 -4.93297e-01 -3.13569e-07
2 p1 6.08502e+00 8.17060e-02 1.10943e-04 1.46657e-04
3 p2 1.75025e+00 5.58927e-02 5.58927e-02 4.35114e-03
fcn flag=0: npar=3 gin=0 par=[ 2333.62 6.08502 1.75025]
histOutputAgorep600
FCN=9.95893 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 255 TOTAL
EDM=7.68343e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33362e+03 7.52367e+01 -4.91867e-01 -3.13944e-07
2 p1 6.08492e+00 8.17291e-02 1.10380e-04 1.51832e-04
3 p2 1.75015e+00 5.58956e-02 5.58956e-02 4.36202e-03
fcn flag=0: npar=3 gin=0 par=[ 2333.62 6.08492 1.75015]
histOutputAgorep650
FCN=10.0019 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 255 TOTAL
EDM=7.28927e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33362e+03 7.52451e+01 -4.91803e-01 -3.15325e-07
2 p1 6.08481e+00 8.17489e-02 1.10227e-04 1.55733e-04
3 p2 1.75008e+00 5.58982e-02 5.58982e-02 4.38803e-03
fcn flag=0: npar=3 gin=0 par=[ 2333.62 6.08481 1.75008]
histOutputAgorep700
FCN=10.0397 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 255 TOTAL
EDM=6.67988e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33361e+03 7.52514e+01 -4.91772e-01 -3.15928e-07
2 p1 6.08470e+00 8.17657e-02 1.10017e-04 1.57180e-04
3 p2 1.75002e+00 5.58996e-02 5.58996e-02 4.42264e-03
fcn flag=0: npar=3 gin=0 par=[ 2333.61 6.0847 1.75002]
histOutputAgorep750
FCN=10.0729 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 255 TOTAL
EDM=5.97099e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33359e+03 7.52571e+01 -4.92602e-01 -3.17344e-07
2 p1 6.08460e+00 8.17799e-02 1.10120e-04 1.58486e-04
3 p2 1.74997e+00 5.59009e-02 5.59009e-02 4.45749e-03
fcn flag=0: npar=3 gin=0 par=[ 2333.59 6.0846 1.74997]
histOutputAgorep800
FCN=10.1021 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 255 TOTAL
EDM=5.24589e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33357e+03 7.52615e+01 -4.93179e-01 -3.17613e-07
2 p1 6.08450e+00 8.17919e-02 1.10026e-04 1.56979e-04
3 p2 1.74993e+00 5.59012e-02 5.59012e-02 4.50445e-03
fcn flag=0: npar=3 gin=0 par=[ 2333.57 6.0845 1.74993]
histOutputAgorep850
FCN=10.1277 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 256 TOTAL
EDM=4.55744e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33354e+03 7.52656e+01 -4.94157e-01 -3.18312e-07
2 p1 6.08441e+00 8.18020e-02 1.10106e-04 1.55635e-04
3 p2 1.74989e+00 5.59013e-02 5.59013e-02 7.26088e-05
fcn flag=0: npar=3 gin=0 par=[ 2333.54 6.08441 1.74989]
histOutputAgorep900
FCN=10.1502 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 256 TOTAL
EDM=3.93388e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33352e+03 7.52692e+01 -4.95114e-01 -3.18961e-07
2 p1 6.08433e+00 8.18107e-02 1.10193e-04 1.54251e-04
3 p2 1.74986e+00 5.59009e-02 5.59009e-02 9.00527e-05
fcn flag=0: npar=3 gin=0 par=[ 2333.52 6.08433 1.74986]
histOutputAgorep950
FCN=10.17 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 256 TOTAL
EDM=3.38618e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33350e+03 7.52723e+01 -4.95951e-01 -3.19059e-07
2 p1 6.08426e+00 8.18183e-02 1.10184e-04 1.51526e-04
3 p2 1.74983e+00 5.59001e-02 5.59001e-02 1.09747e-04
fcn flag=0: npar=3 gin=0 par=[ 2333.5 6.08426 1.74983]
histOutputAgorep1000
FCN=10.1874 FROM MINOS STATUS=SUCCESSFUL 42 CALLS 256 TOTAL
EDM=2.91446e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 p0 2.33349e+03 7.52752e+01 -4.96702e-01 -3.19096e-07
2 p1 6.08419e+00 8.18246e-02 1.10194e-04 1.49019e-04
3 p2 1.74980e+00 5.58989e-02 5.58989e-02 1.24555e-04
fcn flag=0: npar=3 gin=0 par=[ 2333.49 6.08419 1.7498]
"inversion",0.369615,16,0.989,0.687185,13,0.777954,0.843936,6.07588,"±",0.0843187,1.76119,"±",0.0622596
"template",0.220299,16,0.99951,0.640838,13,0.821395,0.834923,6.0667,"±",0.0821739,1.77123,"±",0.0599548
"template+area",0.237251,16,0.999212,0.643779,13,0.818749,0.834905,6.06894,"±",0.0818042,1.77403,"±",0.0597101
"Tikhonov+area",0.567834,16,0.909857,1.70353,13,0.0531425,0.666522,6.01392,"±",0.0830555,1.88219,"±",0.0523609
"min(rhomax)",1.30367,16,0.184004,2.80306,13,0.000506876,0.656519,5.94794,"±",0.0813038,1.96595,"±",0.0470282
"bin-by-bin",4.925,16,2.7358e-10,1.46604,13,0.121301,0,5.90214,"±",0.0816734,2.07111,"±",0.0460711
"iterative, N=0",319.06,16,0,15.2271,13,3.59611e-35,0.849481,5.62399,"±",0.0532143,2.24364,"±",0.0201553
"iterative, N=1",111.402,16,0,9.09211,13,4.5692e-19,0.817166,5.8135,"±",0.0699472,2.27527,"±",0.0262131
"iterative, N=2",62.992,16,2.31021e-204,7.97086,13,3.28626e-16,0.785917,5.89902,"±",0.0771591,2.27417,"±",0.0289737
"iterative, N=3",41.9938,16,1.22802e-132,7.44678,13,6.87329e-15,0.757593,5.93725,"±",0.0805303,2.25891,"±",0.0305064
"iterative, N=4",30.3819,16,2.83616e-93,7.04813,13,6.82474e-14,0.733895,5.9568,"±",0.0823367,2.2385,"±",0.0316079
"iterative, N=5",23.0971,16,8.57418e-69,6.68416,13,5.46969e-13,0.715893,5.96958,"±",0.0835183,2.2164,"±",0.0326294
"iterative, N=6",18.1625,16,2.24797e-52,6.33352,13,4.0031e-12,0.703607,5.98002,"±",0.0844752,2.1935,"±",0.0337655
"iterative, N=7",14.6425,16,8.54613e-41,5.99028,13,2.76604e-11,0.696048,5.99052,"±",0.0854687,2.16994,"±",0.0352059
"iterative, N=8",12.0361,16,2.49723e-32,5.65178,13,1.83018e-10,0.691821,6.0021,"±",0.0867252,2.14524,"±",0.0372357
"iterative, N=9",10.0504,16,5.68598e-26,5.31529,13,1.17568e-09,0.6897,6.01603,"±",0.088702,2.11836,"±",0.0405058
"iterative, N=10",8.50328,16,4.25835e-21,3.27029,13,5.39585e-05,0.688825,6.23206,"±",0.0749655,1.6911,"±",0.0410787
"iterative, N=11",7.27553,16,2.68544e-17,2.98421,13,0.000215602,0.688651,6.21773,"±",0.0753087,1.6883,"±",0.0427987
"iterative, N=12",6.28618,16,2.69801e-14,2.74799,13,0.000654782,0.688847,6.20537,"±",0.075642,1.68766,"±",0.0446099
"iterative, N=13",5.47848,16,6.74681e-12,2.5485,13,0.00162879,0.689213,6.19428,"±",0.0759739,1.68865,"±",0.0464913
"iterative, N=14",4.81161,16,5.78501e-10,2.37666,13,0.00349095,0.68963,6.18428,"±",0.0763206,1.691,"±",0.0484299
"iterative, N=15",4.25556,16,2.15151e-08,2.22618,13,0.00667466,0.690033,6.17507,"±",0.0766907,1.69439,"±",0.0504042
"iterative, N=16",3.78782,16,4.13727e-07,2.09264,13,0.0116635,0.690388,6.1665,"±",0.0770848,1.69854,"±",0.052343
"iterative, N=17",3.3913,16,4.70074e-06,1.97292,13,0.0189482,0.690682,6.15848,"±",0.077509,1.70322,"±",0.0542224
"iterative, N=18",3.05275,16,3.49724e-05,1.8648,13,0.0289726,0.690913,6.15095,"±",0.0779564,1.70817,"±",0.0559703
"iterative, N=19",2.76185,16,0.000184579,1.76668,13,0.0420756,0.691087,6.14388,"±",0.0784164,1.71318,"±",0.0575286
"iterative, N=20",2.51042,16,0.000736128,1.67739,13,0.0584402,0.691212,6.13724,"±",0.0788745,1.71809,"±",0.0588535
"iterative, N=21",2.29192,16,0.00233267,1.59601,13,0.0780608,0.691301,6.13112,"±",0.0793155,1.72273,"±",0.059907
"iterative, N=22",2.10111,16,0.00611486,1.52182,13,0.100738,0.691362,6.1255,"±",0.0797251,1.72699,"±",0.0606866
"iterative, N=23",1.93369,16,0.0136996,1.45417,13,0.126103,0.691407,6.12036,"±",0.0800948,1.73088,"±",0.0612207
"iterative, N=24",1.78617,16,0.0269367,1.39251,13,0.15366,0.691446,6.11571,"±",0.080417,1.73431,"±",0.0615483
"iterative, N=25",1.65566,16,0.0475044,1.33632,13,0.182842,0.691486,6.11149,"±",0.0806925,1.73731,"±",0.0616718
"iterative, N=30",1.18689,16,0.269169,1.12169,13,0.334167,0.691931,6.09634,"±",0.0815191,1.74717,"±",0.0609954
"iterative, N=35",0.908322,16,0.559059,0.984963,13,0.463022,0.69311,6.08782,"±",0.081828,1.75171,"±",0.0597919
"iterative, N=40",0.732607,16,0.762905,0.895558,13,0.557174,0.695148,6.08295,"±",0.0819385,1.75384,"±",0.0588122
"iterative, N=45",0.616619,16,0.873537,0.835466,13,0.622456,0.69795,6.08016,"±",0.0819691,1.75487,"±",0.0580859
"iterative, N=50",0.537326,16,0.92907,0.794103,13,0.667304,0.701338,6.07856,"±",0.0819659,1.75534,"±",0.0575655
"iterative, N=55",0.481626,16,0.95714,0.765088,13,0.698333,0.705124,6.0777,"±",0.0819469,1.75551,"±",0.0571826
"iterative, N=60",0.441666,16,0.971955,0.744448,13,0.720044,0.709144,6.07728,"±",0.081921,1.75556,"±",0.0568981
"iterative, N=65",0.412534,16,0.980214,0.729629,13,0.735393,0.713267,6.07715,"±",0.0818924,1.75548,"±",0.0566806
"iterative, N=70",0.391042,16,0.985078,0.718942,13,0.746319,0.717396,6.0772,"±",0.0818634,1.75538,"±",0.0565139
"iterative, N=75",0.375056,16,0.988086,0.71124,13,0.754111,0.72146,6.07736,"±",0.081835,1.75525,"±",0.0563839
"iterative, N=80",0.363112,16,0.990023,0.705727,13,0.759644,0.725414,6.0776,"±",0.0818081,1.7551,"±",0.056281
"iterative, N=85",0.354178,16,0.991311,0.701838,13,0.763523,0.729226,6.07789,"±",0.0817827,1.75495,"±",0.0561999
"iterative, N=90",0.347516,16,0.992188,0.699169,13,0.766174,0.732878,6.07819,"±",0.0817586,1.75479,"±",0.0561345
"iterative, N=95",0.342588,16,0.992792,0.697424,13,0.767902,0.736361,6.07855,"±",0.0817366,1.75465,"±",0.0560835
"iterative, N=100",0.338996,16,0.99321,0.696381,13,0.768933,0.739673,6.07885,"±",0.0817166,1.7545,"±",0.0560389
"iterative, N=150",0.335268,16,0.993624,0.702102,13,0.763261,0.764528,6.08166,"±",0.0815855,1.75329,"±",0.0558708
"iterative, N=200",0.346127,16,0.992362,0.713822,13,0.751507,0.779298,6.08337,"±",0.0815391,1.75248,"±",0.0558512
"iterative, N=250",0.356914,16,0.990931,0.724381,13,0.740775,0.788781,6.08433,"±",0.0815355,1.75185,"±",0.0558558
"iterative, N=300",0.36599,16,0.989579,0.733328,13,0.731582,0.795305,6.08484,"±",0.0815543,1.75138,"±",0.0558643
"iterative, N=350",0.373445,16,0.988362,0.740928,13,0.723709,0.800037,6.08509,"±",0.0815835,1.75103,"±",0.0558718
"iterative, N=400",0.379583,16,0.987284,0.747449,13,0.71691,0.803611,6.08518,"±",0.0816165,1.75075,"±",0.0558792
"iterative, N=450",0.384672,16,0.986336,0.753092,13,0.710994,0.806396,6.08518,"±",0.081649,1.75054,"±",0.0558845
"iterative, N=500",0.388923,16,0.985505,0.758007,13,0.705821,0.808621,6.08512,"±",0.0816791,1.75037,"±",0.0558888
"iterative, N=550",0.3925,16,0.984779,0.762304,13,0.701281,0.810434,6.08502,"±",0.081706,1.75025,"±",0.0558927
"iterative, N=600",0.395528,16,0.984143,0.766072,13,0.697289,0.811937,6.08492,"±",0.0817291,1.75015,"±",0.0558956
"iterative, N=650",0.398104,16,0.983588,0.76938,13,0.693776,0.813199,6.08481,"±",0.0817489,1.75008,"±",0.0558982
"iterative, N=700",0.400304,16,0.983103,0.772286,13,0.690683,0.814272,6.0847,"±",0.0817657,1.75002,"±",0.0558996
"iterative, N=750",0.40219,16,0.982678,0.77484,13,0.687961,0.815194,6.0846,"±",0.0817799,1.74997,"±",0.0559009
"iterative, N=800",0.403812,16,0.982307,0.777084,13,0.685565,0.815995,6.0845,"±",0.0817919,1.74993,"±",0.0559012
"iterative, N=850",0.40521,16,0.981983,0.779056,13,0.683458,0.816697,6.08441,"±",0.081802,1.74989,"±",0.0559013
"iterative, N=900",0.406417,16,0.9817,0.780788,13,0.681605,0.817318,6.08433,"±",0.0818107,1.74986,"±",0.0559009
"iterative, N=950",0.407463,16,0.981452,0.78231,13,0.679975,0.817871,6.08426,"±",0.0818183,1.74983,"±",0.0559001
"iterative, N=1000",0.408369,16,0.981235,0.783648,13,0.678541,0.818368,6.08419,"±",0.0818246,1.7498,"±",0.0558989
#include <iostream>
#include <cmath>
#include <map>
#include <TMath.h>
#include <TCanvas.h>
#include <TStyle.h>
#include <TGraph.h>
#include <TGraphErrors.h>
#include <TFile.h>
#include <TROOT.h>
#include <TText.h>
#include <TLine.h>
#include <TLegend.h>
#include <TH1.h>
#include <TF1.h>
#include <TFitter.h>
#include <TMatrixD.h>
#include <TMatrixDSym.h>
#include <TVectorD.h>
#include <TMatrixDSymEigen.h>
#include <TFitResult.h>
#include <TRandom3.h>
#include "TUnfoldDensity.h"
using namespace std;
// #define PRINT_MATRIX_L
#define TEST_INPUT_COVARIANCE
void CreateHistogramCopies(TH1 *h[3],TUnfoldBinning const *binning);
void CreateHistogramCopies(TH2 *h[3],TUnfoldBinning const *binningX);
TH2 *AddOverflowXY(TH2 *h,double widthX,double widthY);
TH1 *AddOverflowX(TH1 *h,double width);
void DrawOverflowX(TH1 *h,double posy);
void DrawOverflowY(TH1 *h,double posx);
double const kLegendFontSize=0.05;
int kNbinC=0;
void DrawPadProbability(TH2 *h);
void DrawPadEfficiency(TH1 *h);
void DrawPadReco(TH1 *histMcRec,TH1 *histMcbgrRec,TH1 *histDataRec,
TH1 *histDataUnfold,TH2 *histProbability,TH2 *histRhoij);
void DrawPadTruth(TH1 *histMcsigGen,TH1 *histDataGen,TH1 *histDataUnfold,
char const *text=0,double tau=0.0,vector<double> const *r=0,
TF1 *f=0);
void DrawPadCorrelations(TH2 *h,
vector<pair<TF1*,vector<double> > > const *table);
TFitResultPtr DoFit(TH1 *h,TH2 *rho,TH1 *truth,char const *text,
vector<pair<TF1*,vector<double> > > &table,int niter=0);
void GetNiterGraphs(int iFirst,int iLast,vector<pair<TF1*,
vector<double> > > const &table,int color,
TGraph *graph[4],int style);
void GetNiterHist(int ifit,vector<pair<TF1*,vector<double> > > const &table,
TH1 *hist[4],int color,int style,int fillStyle);
#ifdef WITH_IDS
void IDSfirst(TVectorD *data, TVectorD *dataErr, TMatrixD *A_, Double_t lambdaL_, TVectorD* &unfres1IDS_,TVectorD *&soustr);
void IDSiterate(TVectorD *data, TVectorD *dataErr, TMatrixD *A_,TMatrixD *Am_,
Double_t lambdaU_, Double_t lambdaM_, Double_t lambdaS_,
TVectorD* &unfres2IDS_ ,TVectorD *&soustr);
#endif
TRandom3 *g_rnd;
void testUnfold7c()
{
gErrorIgnoreLevel=kInfo;
// switch on histogram errors
TH1::SetDefaultSumw2();
gStyle->SetOptStat(0);
g_rnd=new TRandom3(4711);
//==============================================
// step 1 : open output file
TFile *outputFile=new TFile("testUnfold7_results.root","recreate");
//==============================================
// step 2 : read binning schemes and input histograms
TFile *inputFile=new TFile("testUnfold7_histograms.root");
outputFile->cd();
TUnfoldBinning *fineBinning,*coarseBinning;
inputFile->GetObject("fine",fineBinning);
inputFile->GetObject("coarse",coarseBinning);
if((!fineBinning)||(!coarseBinning)) {
cout<<"problem to read binning schemes\n";
}
// save binning schemes to output file
fineBinning->Write();
coarseBinning->Write();
// read histograms
#define READ(TYPE,binning,name) \
TYPE *name[3]; inputFile->GetObject(#name,name[0]); \
name[0]->Write(); \
if(!name[0]) cout<<"Error reading " #name "\n"; \
CreateHistogramCopies(name,binning);
outputFile->cd();
READ(TH1,fineBinning,histDataRecF);
READ(TH1,coarseBinning,histDataRecC);
READ(TH1,fineBinning,histDataBgrF);
READ(TH1,coarseBinning,histDataBgrC);
READ(TH1,coarseBinning,histDataGen);
READ(TH2,fineBinning,histMcsigGenRecF);
READ(TH2,coarseBinning,histMcsigGenRecC);
READ(TH1,fineBinning,histMcsigRecF);
READ(TH1,coarseBinning,histMcsigRecC);
READ(TH1,coarseBinning,histMcsigGen);
READ(TH1,fineBinning,histMcbgrRecF);
READ(TH1,coarseBinning,histMcbgrRecC);
TH1 *histOutputCtau0[3];
TH2 *histRhoCtau0;
TH1 *histOutputCLCurve[3];
//TH2 *histRhoCLCurve;
TH2 *histProbC;
double tauMin=1.e-4;
double tauMax=1.e-1;
double fBgr=1.0; // 0.2/0.25;
double biasScale=1.0;
TUnfold::ERegMode mode=TUnfold::kRegModeSize; //Derivative;
//double tauC;
{
TUnfoldDensity *tunfoldC=
new TUnfoldDensity(histMcsigGenRecC[0],
TUnfold::kHistMapOutputHoriz,
mode,
TUnfold::kEConstraintNone,//Area,
TUnfoldDensity::kDensityModeNone,
coarseBinning,
coarseBinning);
tunfoldC->SetInput(histDataRecC[0],biasScale);
tunfoldC->SubtractBackground(histMcbgrRecC[0],"BGR",fBgr,0.0);
tunfoldC->DoUnfold(0.);
histOutputCtau0[0]=tunfoldC->GetOutput("histOutputCtau0");
histRhoCtau0=tunfoldC->GetRhoIJtotal("histRhoCtau0");
CreateHistogramCopies(histOutputCtau0,coarseBinning);
tunfoldC->ScanLcurve(50,tauMin,tauMax,0);
/* tauC= */tunfoldC->GetTau();
//tunfoldC->ScanTau(50,1.E-7,1.E-1,0,TUnfoldDensity::kEScanTauRhoAvg);
histOutputCLCurve[0]=tunfoldC->GetOutput("histOutputCLCurve");
/* histRhoCLCurve= */tunfoldC->GetRhoIJtotal("histRhoCLCurve");
CreateHistogramCopies(histOutputCLCurve,coarseBinning);
histProbC=tunfoldC->GetProbabilityMatrix("histProbC",";P_T(gen);P_T(rec)");
}
TH1 *histOutputFtau0[3];
TH2 *histRhoFtau0;
TH1 *histOutputFLCurve[3];
//TH2 *histRhoFLCurve;
TH2 *histProbF;
TGraph *lCurve;
TSpline *logTauX,*logTauY;
tauMin=3.E-4;
tauMax=3.E-2;
//double tauF;
{
TUnfoldDensity *tunfoldF=
new TUnfoldDensity(histMcsigGenRecF[0],
TUnfold::kHistMapOutputHoriz,
mode,
TUnfold::kEConstraintNone,//Area,
TUnfoldDensity::kDensityModeNone,
coarseBinning,
fineBinning);
tunfoldF->SetInput(histDataRecF[0],biasScale);
tunfoldF->SubtractBackground(histMcbgrRecF[0],"BGR",fBgr,0.0);
tunfoldF->DoUnfold(0.);
histOutputFtau0[0]=tunfoldF->GetOutput("histOutputFtau0");
histRhoFtau0=tunfoldF->GetRhoIJtotal("histRhoFtau0");
CreateHistogramCopies(histOutputFtau0,coarseBinning);
tunfoldF->ScanLcurve(50,tauMin,tauMax,0);
//tunfoldF->DoUnfold(tauC);
/* tauF= */tunfoldF->GetTau();
//tunfoldF->ScanTau(50,1.E-7,1.E-1,0,TUnfoldDensity::kEScanTauRhoAvg);
histOutputFLCurve[0]=tunfoldF->GetOutput("histOutputFLCurve");
/* histRhoFLCurve= */tunfoldF->GetRhoIJtotal("histRhoFLCurve");
CreateHistogramCopies(histOutputFLCurve,coarseBinning);
histProbF=tunfoldF->GetProbabilityMatrix("histProbF",";P_T(gen);P_T(rec)");
}
TH1 *histOutputFAtau0[3];
TH2 *histRhoFAtau0;
TH1 *histOutputFALCurve[3];
TH2 *histRhoFALCurve;
TH1 *histOutputFArho[3];
TH2 *histRhoFArho;
TSpline *rhoScan=0;
TSpline *logTauCurvature=0;
double tauFA,tauFArho;
{
TUnfoldDensity *tunfoldFA=
new TUnfoldDensity(histMcsigGenRecF[0],
TUnfold::kHistMapOutputHoriz,
mode,
TUnfold::kEConstraintArea,
TUnfoldDensity::kDensityModeNone,
coarseBinning,
fineBinning);
tunfoldFA->SetInput(histDataRecF[0],biasScale);
tunfoldFA->SubtractBackground(histMcbgrRecF[0],"BGR",fBgr,0.0);
tunfoldFA->DoUnfold(0.);
histOutputFAtau0[0]=tunfoldFA->GetOutput("histOutputFAtau0");
histRhoFAtau0=tunfoldFA->GetRhoIJtotal("histRhoFAtau0");
CreateHistogramCopies(histOutputFAtau0,coarseBinning);
tunfoldFA->ScanTau(50,tauMin,tauMax,&rhoScan,TUnfoldDensity::kEScanTauRhoAvg);
tauFArho=tunfoldFA->GetTau();
histOutputFArho[0]=tunfoldFA->GetOutput("histOutputFArho");
histRhoFArho=tunfoldFA->GetRhoIJtotal("histRhoFArho");
CreateHistogramCopies(histOutputFArho,coarseBinning);
tunfoldFA->ScanLcurve(50,tauMin,tauMax,&lCurve,&logTauX,&logTauY,&logTauCurvature);
tauFA=tunfoldFA->GetTau();
histOutputFALCurve[0]=tunfoldFA->GetOutput("histOutputFALCurve");
histRhoFALCurve=tunfoldFA->GetRhoIJtotal("histRhoFALCurve");
CreateHistogramCopies(histOutputFALCurve,coarseBinning);
}
lCurve->Write();
logTauX->Write();
logTauY->Write();
double widthC=coarseBinning->GetBinSize(histProbC->GetNbinsY()+1);
double widthF=fineBinning->GetBinSize(histProbF->GetNbinsY()+1);
TH2 *histProbCO=AddOverflowXY(histProbC,widthC,widthC);
TH2 *histProbFO=AddOverflowXY(histProbF,widthC,widthF);
// efficiency
TH1 *histEfficiencyC=histProbCO->ProjectionX("histEfficiencyC");
kNbinC=histProbCO->GetNbinsX();
// reconstructed quantities with overflow (coarse binning)
// MC: add signal and bgr
TH1 *histMcsigRecCO=AddOverflowX(histMcsigRecC[2],widthC);
TH1 *histMcbgrRecCO=AddOverflowX(histMcbgrRecC[2],widthC);
histMcbgrRecCO->Scale(fBgr);
TH1 *histMcRecCO=(TH1 *)histMcsigRecCO->Clone("histMcRecC0");
histMcRecCO->Add(histMcsigRecCO,histMcbgrRecCO);
TH1 *histDataRecCO=AddOverflowX(histDataRecC[2],widthC);
//TH1 *histDataRecCNO=AddOverflowX(histDataRecC[1],widthC);
TH1 *histMcsigRecFO=AddOverflowX(histMcsigRecF[2],widthF);
TH1 *histMcbgrRecFO=AddOverflowX(histMcbgrRecF[2],widthF);
histMcbgrRecFO->Scale(fBgr);
TH1 *histMcRecFO=(TH1 *)histMcsigRecFO->Clone("histMcRecF0");
histMcRecFO->Add(histMcsigRecFO,histMcbgrRecFO);
TH1 *histDataRecFO=AddOverflowX(histDataRecF[2],widthF);
// truth level with overflow
TH1 *histMcsigGenO=AddOverflowX(histMcsigGen[2],widthC);
TH1 *histDataGenO=AddOverflowX(histDataGen[2],widthC);
// unfolding result with overflow
TH1 *histOutputCtau0O=AddOverflowX(histOutputCtau0[2],widthC);
TH2 *histRhoCtau0O=AddOverflowXY(histRhoCtau0,widthC,widthC);
//TH1 *histOutputCLCurveO=AddOverflowX(histOutputCLCurve[2],widthC);
//TH2 *histRhoCLCurveO=AddOverflowXY(histRhoCLCurve,widthC,widthC);
TH1 *histOutputFtau0O=AddOverflowX(histOutputFtau0[2],widthC);
TH2 *histRhoFtau0O=AddOverflowXY(histRhoFtau0,widthC,widthC);
TH1 *histOutputFAtau0O=AddOverflowX(histOutputFAtau0[2],widthC);
TH2 *histRhoFAtau0O=AddOverflowXY(histRhoFAtau0,widthC,widthC);
//TH1 *histOutputFLCurveO=AddOverflowX(histOutputFLCurve[2],widthC);
//TH2 *histRhoFLCurveO=AddOverflowXY(histRhoFLCurve,widthC,widthC);
TH1 *histOutputFALCurveO=AddOverflowX(histOutputFALCurve[2],widthC);
TH2 *histRhoFALCurveO=AddOverflowXY(histRhoFALCurve,widthC,widthC);
TH1 *histOutputFArhoO=AddOverflowX(histOutputFArho[2],widthC);
TH2 *histRhoFArhoO=AddOverflowXY(histRhoFArho,widthC,widthC);
// bin-by-bin
TH2 *histRhoBBBO=(TH2 *)histRhoCtau0O->Clone("histRhoBBBO");
for(int i=1;i<=histRhoBBBO->GetNbinsX();i++) {
for(int j=1;j<=histRhoBBBO->GetNbinsX();j++) {
histRhoBBBO->SetBinContent(i,j,(i==j)?1.:0.);
}
}
TH1 *histDataBgrsub=(TH1 *)histDataRecCO->Clone("histDataBgrsub");
histDataBgrsub->Add(histMcbgrRecCO,-fBgr);
TH1 *histOutputBBBO=(TH1 *)histDataBgrsub->Clone("histOutputBBBO");
histOutputBBBO->Divide(histMcsigRecCO);
histOutputBBBO->Multiply(histMcsigGenO);
// iterative
int niter=1000;
cout<<"maximum number of iterations: "<<niter<<"\n";
vector <TH1 *>histOutputAgo,histOutputAgorep;
vector <TH2 *>histRhoAgo,histRhoAgorep;
vector<int> nIter;
histOutputAgo.push_back((TH1*)histMcsigGenO->Clone("histOutputAgo-1"));
histOutputAgorep.push_back((TH1*)histMcsigGenO->Clone("histOutputAgorep-1"));
histRhoAgo.push_back((TH2*)histRhoBBBO->Clone("histRhoAgo-1"));
histRhoAgorep.push_back((TH2*)histRhoBBBO->Clone("histRhoAgorep-1"));
nIter.push_back(-1);
int nx=histProbCO->GetNbinsX();
int ny=histProbCO->GetNbinsY();
TMatrixD covAgo(nx+ny,nx+ny);
TMatrixD A(ny,nx);
TMatrixD AToverEps(nx,ny);
for(int i=0;i<nx;i++) {
double epsilonI=0.;
for(int j=0;j<ny;j++) {
epsilonI+= histProbCO->GetBinContent(i+1,j+1);
}
for(int j=0;j<ny;j++) {
double aji=histProbCO->GetBinContent(i+1,j+1);
A(j,i)=aji;
AToverEps(i,j)=aji/epsilonI;
}
}
for(int i=0;i<nx;i++) {
covAgo(i,i)=TMath::Power
(histOutputAgo[0]->GetBinError(i+1)
*histOutputAgo[0]->GetXaxis()->GetBinWidth(i+1),2.);
}
for(int i=0;i<ny;i++) {
covAgo(i+nx,i+nx)=TMath::Power
(histDataRecCO->GetBinError(i+1)
*histDataRecCO->GetXaxis()->GetBinWidth(i+1),2.);
}
#define NREPLICA 300
vector<TVectorD *> y(NREPLICA);
vector<TVectorD *> yMb(NREPLICA);
vector<TVectorD *> yErr(NREPLICA);
vector<TVectorD *> x(NREPLICA);
TVectorD b(nx);
for(int nr=0;nr<NREPLICA;nr++) {
x[nr]=new TVectorD(nx);
y[nr]=new TVectorD(ny);
yMb[nr]=new TVectorD(ny);
yErr[nr]=new TVectorD(ny);
}
for(int i=0;i<nx;i++) {
(*x[0])(i)=histOutputAgo[0]->GetBinContent(i+1)
*histOutputAgo[0]->GetXaxis()->GetBinWidth(i+1);
for(int nr=1;nr<NREPLICA;nr++) {
(*x[nr])(i)=(*x[0])(i);
}
}
for(int i=0;i<ny;i++) {
(*y[0])(i)=histDataRecCO->GetBinContent(i+1)
*histDataRecCO->GetXaxis()->GetBinWidth(i+1);
for(int nr=1;nr<NREPLICA;nr++) {
(*y[nr])(i)=g_rnd->Poisson((*y[0])(i));
(*yErr[nr])(i)=TMath::Sqrt((*y[nr])(i));
}
b(i)=histMcbgrRecCO->GetBinContent(i+1)*
histMcbgrRecCO->GetXaxis()->GetBinWidth(i+1);
for(int nr=0;nr<NREPLICA;nr++) {
(*yMb[nr])(i)=(*y[nr])(i)-b(i);
}
}
for(int iter=0;iter<=niter;iter++) {
if(!(iter %100)) cout<<iter<<"\n";
for(int nr=0;nr<NREPLICA;nr++) {
TVectorD yrec=A*(*x[nr])+b;
TVectorD yOverYrec(ny);
for(int j=0;j<ny;j++) {
yOverYrec(j)=(*y[nr])(j)/yrec(j);
}
TVectorD f=AToverEps * yOverYrec;
TVectorD xx(nx);
for(int i=0;i<nx;i++) {
xx(i) = (*x[nr])(i) * f(i);
}
if(nr==0) {
TMatrixD xdf_dr=AToverEps;
for(int i=0;i<nx;i++) {
for(int j=0;j<ny;j++) {
xdf_dr(i,j) *= (*x[nr])(i);
}
}
TMatrixD dr_dxdy(ny,nx+ny);
for(int j=0;j<ny;j++) {
dr_dxdy(j,nx+j)=1.0/yrec(j);
for(int i=0;i<nx;i++) {
dr_dxdy(j,i)= -yOverYrec(j)/yrec(j)*A(j,i);
}
}
TMatrixD dxy_dxy(nx+ny,nx+ny);
dxy_dxy.SetSub(0,0,xdf_dr*dr_dxdy);
for(int i=0;i<nx;i++) {
dxy_dxy(i,i) +=f(i);
}
for(int i=0;i<ny;i++) {
dxy_dxy(nx+i,nx+i) +=1.0;
}
TMatrixD VDT(covAgo,TMatrixD::kMultTranspose,dxy_dxy);
covAgo= dxy_dxy*VDT;
}
(*x[nr])=xx;
}
if((iter<=25)||
((iter<=100)&&(iter %5==0))||
((iter<=1000)&&(iter %50==0))||
(iter %1000==0)) {
nIter.push_back(iter);
TH1 * h=(TH1*)histOutputAgo[0]->Clone
(TString::Format("histOutputAgo%d",iter));
histOutputAgo.push_back(h);
for(int i=0;i<nx;i++) {
double bw=h->GetXaxis()->GetBinWidth(i+1);
h->SetBinContent(i+1,(*x[0])(i)/bw);
h->SetBinError(i+1,TMath::Sqrt(covAgo(i,i))/bw);
}
TH2 *h2=(TH2*)histRhoAgo[0]->Clone
(TString::Format("histRhoAgo%d",iter));
histRhoAgo.push_back(h2);
for(int i=0;i<nx;i++) {
for(int j=0;j<nx;j++) {
double rho= covAgo(i,j)/TMath::Sqrt(covAgo(i,i)*covAgo(j,j));
if((i!=j)&&(TMath::Abs(rho)>=1.0)) {
cout<<"bad error matrix: iter="<<iter<<"\n";
exit(0);
}
h2->SetBinContent(i+1,j+1,rho);
}
}
// error and correlations from replica analysis
h=(TH1*)histOutputAgo[0]->Clone
(TString::Format("histOutputAgorep%d",iter));
h2=(TH2*)histRhoAgo[0]->Clone
(TString::Format("histRhoAgorep%d",iter));
histOutputAgorep.push_back(h);
histRhoAgorep.push_back(h2);
TVectorD mean(nx);
double w=1./(NREPLICA-1.);
for(int nr=1;nr<NREPLICA;nr++) {
mean += w* *x[nr];
}
TMatrixD covAgorep(nx,nx);
for(int nr=1;nr<NREPLICA;nr++) {
//TMatrixD dx= (*x)-mean;
TMatrixD dx(nx,1);
for(int i=0;i<nx;i++) {
dx(i,0)= (*x[nr])(i)-(*x[0])(i);
}
covAgorep += w*TMatrixD(dx,TMatrixD::kMultTranspose,dx);
}
for(int i=0;i<nx;i++) {
double bw=h->GetXaxis()->GetBinWidth(i+1);
h->SetBinContent(i+1,(*x[0])(i)/bw);
h->SetBinError(i+1,TMath::Sqrt(covAgorep(i,i))/bw);
// cout<<i<<" "<<(*x[0])(i)/bw<<" +/-"<<TMath::Sqrt(covAgorep(i,i))/bw<<" "<<TMath::Sqrt(covAgo(i,i))/bw<<"\n";
}
for(int i=0;i<nx;i++) {
for(int j=0;j<nx;j++) {
double rho= covAgorep(i,j)/
TMath::Sqrt(covAgorep(i,i)*covAgorep(j,j));
if((i!=j)&&(TMath::Abs(rho)>=1.0)) {
cout<<"bad error matrix: iter="<<iter<<"\n";
exit(0);
}
h2->SetBinContent(i+1,j+1,rho);
}
}
}
}
#ifdef WITH_IDS
// IDS Malaescu
int niterIDS=100;
vector<TVectorD*> unfresIDS(NREPLICA),soustr(NREPLICA);
cout<<"IDS number of iterations: "<<niterIDS<<"\n";
TMatrixD *Am_IDS[NREPLICA];
TMatrixD A_IDS(ny,nx);
for(int nr=0;nr<NREPLICA;nr++) {
Am_IDS[nr]=new TMatrixD(ny,nx);
}
for(int iy=0;iy<ny;iy++) {
for(int ix=0;ix<nx;ix++) {
A_IDS(iy,ix)=histMcsigGenRecC[0]->GetBinContent(ix+1,iy+1);
}
}
double lambdaL=0.;
Double_t lambdaUmin = 1.0000002;
Double_t lambdaMmin = 0.0000001;
Double_t lambdaS = 0.000001;
double lambdaU=lambdaUmin;
double lambdaM=lambdaMmin;
vector<TH1 *> histOutputIDS;
vector<TH2 *> histRhoIDS;
histOutputIDS.push_back((TH1*)histOutputAgo[0]->Clone("histOutputIDS-1"));
histRhoIDS.push_back((TH2*)histRhoAgo[0]->Clone("histRhoIDS-1"));
histOutputIDS.push_back((TH1*)histOutputAgo[0]->Clone("histOutputIDS0"));
histRhoIDS.push_back((TH2*)histRhoAgo[0]->Clone("histRhoIDS0"));
for(int iter=1;iter<=niterIDS;iter++) {
if(!(iter %10)) cout<<iter<<"\n";
for(int nr=0;nr<NREPLICA;nr++) {
if(iter==1) {
IDSfirst(yMb[nr],yErr[nr],&A_IDS,lambdaL,unfresIDS[nr],soustr[nr]);
} else {
IDSiterate(yMb[nr],yErr[nr],&A_IDS,Am_IDS[nr],
lambdaU,lambdaM,lambdaS,
unfresIDS[nr],soustr[nr]);
}
}
unsigned ix;
for(ix=0;ix<nIter.size();ix++) {
if(nIter[ix]==iter) break;
}
if(ix<nIter.size()) {
TH1 * h=(TH1*)histOutputIDS[0]->Clone
(TString::Format("histOutputIDS%d",iter));
TH2 *h2=(TH2*)histRhoIDS[0]->Clone
(TString::Format("histRhoIDS%d",iter));
histOutputIDS.push_back(h);
histRhoIDS.push_back(h2);
TVectorD mean(nx);
double w=1./(NREPLICA-1.);
for(int nr=1;nr<NREPLICA;nr++) {
mean += w* (*unfresIDS[nr]);
}
TMatrixD covIDSrep(nx,nx);
for(int nr=1;nr<NREPLICA;nr++) {
//TMatrixD dx= (*x)-mean;
TMatrixD dx(nx,1);
for(int i=0;i<nx;i++) {
dx(i,0)= (*unfresIDS[nr])(i)-(*unfresIDS[0])(i);
}
covIDSrep += w*TMatrixD(dx,TMatrixD::kMultTranspose,dx);
}
for(int i=0;i<nx;i++) {
double bw=h->GetXaxis()->GetBinWidth(i+1);
h->SetBinContent(i+1,(*unfresIDS[0])(i)/bw/
histEfficiencyC->GetBinContent(i+1));
h->SetBinError(i+1,TMath::Sqrt(covIDSrep(i,i))/bw/
histEfficiencyC->GetBinContent(i+1));
// cout<<i<<" "<<(*x[0])(i)/bw<<" +/-"<<TMath::Sqrt(covAgorep(i,i))/bw<<" "<<TMath::Sqrt(covAgo(i,i))/bw<<"\n";
}
for(int i=0;i<nx;i++) {
for(int j=0;j<nx;j++) {
double rho= covIDSrep(i,j)/
TMath::Sqrt(covIDSrep(i,i)*covIDSrep(j,j));
if((i!=j)&&(TMath::Abs(rho)>=1.0)) {
cout<<"bad error matrix: iter="<<iter<<"\n";
exit(0);
}
h2->SetBinContent(i+1,j+1,rho);
}
}
}
}
#endif
//double NEdSmc=histDataBgrsub->GetSumOfWeights();
vector<pair<TF1 *,vector<double> > > table;
TCanvas *c1=new TCanvas("c1","",600,600);
TCanvas *c2sq=new TCanvas("c2sq","",600,600);
c2sq->Divide(1,2);
TCanvas *c2w=new TCanvas("c2w","",600,300);
c2w->Divide(2,1);
TCanvas *c4=new TCanvas("c4","",600,600);
c4->Divide(2,2);
//TCanvas *c3n=new TCanvas("c3n","",600,600);
TPad *subn[3];
//gROOT->SetStyle("xTimes2");
subn[0]= new TPad("subn0","",0.,0.5,1.,1.);
//gROOT->SetStyle("square");
subn[1]= new TPad("subn1","",0.,0.,0.5,0.5);
subn[2]= new TPad("subn2","",0.5,0.0,1.,0.5);
for(int i=0;i<3;i++) {
subn[i]->SetFillStyle(0);
subn[i]->Draw();
}
TCanvas *c3c=new TCanvas("c3c","",600,600);
TPad *subc[3];
//gROOT->SetStyle("xTimes2");
subc[0]= new TPad("sub0","",0.,0.5,1.,1.);
//gROOT->SetStyle("squareCOLZ");
subc[1]= new TPad("sub1","",0.,0.,0.5,0.5);
//gROOT->SetStyle("square");
subc[2]= new TPad("sub2","",0.5,0.0,1.,0.5);
for(int i=0;i<3;i++) {
subc[i]->SetFillStyle(0);
subc[i]->Draw();
}
//=========================== example ==================================
c2w->cd(1);
DrawPadTruth(histMcsigGenO,histDataGenO,0);
c2w->cd(2);
DrawPadReco(histMcRecCO,histMcbgrRecCO,histDataRecCO,0,0,0);
c2w->SaveAs("exampleTR.eps");
//=========================== example ==================================
c2w->cd(1);
DrawPadProbability(histProbCO);
c2w->cd(2);
DrawPadEfficiency(histEfficiencyC);
c2w->SaveAs("exampleAE.eps");
int iFitInversion=table.size();
DoFit(histOutputCtau0O,histRhoCtau0O,histDataGenO,"inversion",table);
//=========================== inversion ==================================
subc[0]->cd();
DrawPadTruth(histMcsigGenO,histDataGenO,histOutputCtau0O,"inversion",0.,
&table[table.size()-1].second);
subc[1]->cd();
DrawPadCorrelations(histRhoCtau0O,&table);
subc[2]->cd();
DrawPadReco(histMcRecCO,histMcbgrRecCO,histDataRecCO,
histOutputCtau0O,histProbCO,histRhoCtau0O);
c3c->SaveAs("inversion.eps");
DoFit(histOutputFtau0O,histRhoFtau0O,histDataGenO,"template",table);
//=========================== template ==================================
subc[0]->cd();
DrawPadTruth(histMcsigGenO,histDataGenO,histOutputFtau0O,"fit",0.,
&table[table.size()-1].second);
subc[1]->cd();
DrawPadCorrelations(histRhoFtau0O,&table);
subc[2]->cd();
DrawPadReco(histMcRecFO,histMcbgrRecFO,histDataRecFO,
histOutputFtau0O,histProbFO,histRhoFtau0O);
c3c->SaveAs("template.eps");
DoFit(histOutputFAtau0O,histRhoFAtau0O,histDataGenO,"template+area",table);
//=========================== template+area ==================================
subc[0]->cd();
DrawPadTruth(histMcsigGenO,histDataGenO,histOutputFAtau0O,"fit",0.,
&table[table.size()-1].second);
subc[1]->cd();
DrawPadCorrelations(histRhoFAtau0O,&table);
subc[2]->cd();
DrawPadReco(histMcRecFO,histMcbgrRecFO,histDataRecFO,
histOutputFAtau0O,histProbFO,histRhoFAtau0O);
c3c->SaveAs("templateA.eps");
int iFitFALCurve=table.size();
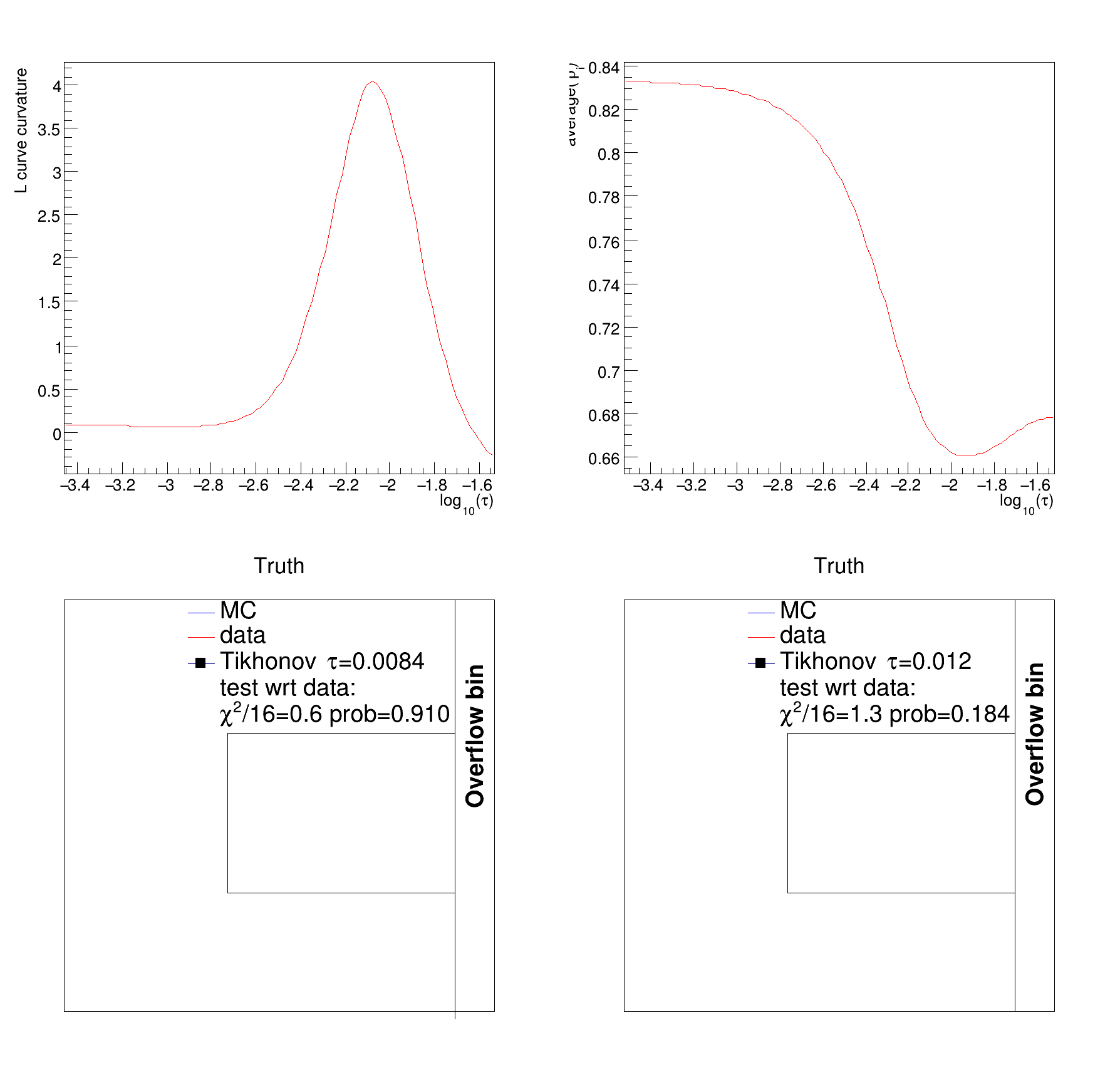
DoFit(histOutputFALCurveO,histRhoFALCurveO,histDataGenO,"Tikhonov+area",table);
//=========================== template+area+tikhonov =====================
subc[0]->cd();
DrawPadTruth(histMcsigGenO,histDataGenO,histOutputFALCurveO,"Tikhonov",tauFA,
&table[table.size()-1].second);
subc[1]->cd();
DrawPadCorrelations(histRhoFALCurveO,&table);
subc[2]->cd();
DrawPadReco(histMcRecFO,histMcbgrRecFO,histDataRecFO,
histOutputFALCurveO,histProbFO,histRhoFALCurveO);
c3c->SaveAs("lcurveFA.eps");
int iFitFArho=table.size();
DoFit(histOutputFArhoO,histRhoFArhoO,histDataGenO,"min(rhomax)",table);
//=========================== template+area+tikhonov =====================
subc[0]->cd();
DrawPadTruth(histMcsigGenO,histDataGenO,histOutputFArhoO,"Tikhonov",tauFArho,
&table[table.size()-1].second);
subc[1]->cd();
DrawPadCorrelations(histRhoFArho,&table);
subc[2]->cd();
DrawPadReco(histMcRecFO,histMcbgrRecFO,histDataRecFO,
histOutputFArhoO,histProbFO,histRhoFArhoO);
c3c->SaveAs("rhoscanFA.eps");
int iFitBinByBin=table.size();
DoFit(histOutputBBBO,histRhoBBBO,histDataGenO,"bin-by-bin",table);
//=========================== bin-by-bin =================================
//c->cd(1);
//DrawPadProbability(histProbCO);
//c->cd(2);
//DrawPadCorrelations(histRhoBBBO,&table);
c2sq->cd(1);
DrawPadReco(histMcRecCO,histMcbgrRecCO,histDataRecCO,
histOutputBBBO,histProbCO,histRhoBBBO);
c2sq->cd(2);
DrawPadTruth(histMcsigGenO,histDataGenO,histOutputBBBO,"bin-by-bin",0.,
&table[table.size()-1].second);
c2sq->SaveAs("binbybin.eps");
//=========================== iterative ===================================
int iAgoFirstFit=table.size();
for(size_t i=1;i<histRhoAgorep.size();i++) {
int n=nIter[i];
bool isFitted=false;
DoFit(histOutputAgorep[i],histRhoAgorep[i],histDataGenO,
TString::Format("iterative, N=%d",n),table,n);
isFitted=true;
subc[0]->cd();
DrawPadTruth(histMcsigGenO,histDataGenO,histOutputAgorep[i],
TString::Format("iterative N=%d",nIter[i]),0.,
isFitted ? &table[table.size()-1].second : 0);
subc[1]->cd();
DrawPadCorrelations(histRhoAgorep[i],&table);
subc[2]->cd();
DrawPadReco(histMcRecCO,histMcbgrRecCO,histDataRecCO,
histOutputAgorep[i],histProbCO,histRhoAgorep[i]);
c3c->SaveAs(TString::Format("iterative%d.eps",nIter[i]));
}
int iAgoLastFit=table.size();
#ifdef WITH_IDS
int iIDSFirstFit=table.size();
//=========================== IDS ===================================
for(size_t i=2;i<histRhoIDS.size();i++) {
int n=nIter[i];
bool isFitted=false;
DoFit(histOutputIDS[i],histRhoIDS[i],histDataGenO,
TString::Format("IDS, N=%d",n),table,n);
isFitted=true;
subc[0]->cd();
DrawPadTruth(histMcsigGenO,histDataGenO,histOutputIDS[i],
TString::Format("IDS N=%d",nIter[i]),0.,
isFitted ? &table[table.size()-1].second : 0);
subc[1]->cd();
DrawPadCorrelations(histRhoIDS[i],&table);
subc[2]->cd();
DrawPadReco(histMcRecCO,histMcbgrRecCO,histDataRecCO,
histOutputIDS[i],histProbCO,histRhoIDS[i]);
c3c->SaveAs(TString::Format("ids%d.eps",nIter[i]));
}
int iIDSLastFit=table.size();
#endif
int nfit=table.size();
TH1D *fitChindf=new TH1D("fitChindf",";algorithm;#chi^{2}/NDF",nfit,0,nfit);
TH1D *fitNorm=new TH1D("fitNorm",";algorithm;Landau amplitude [1/GeV]",nfit,0,nfit);
TH1D *fitMu=new TH1D("fitMu",";algorithm;Landau #mu [GeV]",nfit,0,nfit);
TH1D *fitSigma=new TH1D("fitSigma",";algorithm;Landau #sigma [GeV]",nfit,0,nfit);
for(int fit=0;fit<nfit;fit++) {
TF1 *f=table[fit].first;
vector<double> const &r=table[fit].second;
fitChindf->GetXaxis()->SetBinLabel(fit+1,f->GetName());
fitNorm->GetXaxis()->SetBinLabel(fit+1,f->GetName());
fitMu->GetXaxis()->SetBinLabel(fit+1,f->GetName());
fitSigma->GetXaxis()->SetBinLabel(fit+1,f->GetName());
double chi2=r[0];
double ndf=r[1];
fitChindf->SetBinContent(fit+1,chi2/ndf);
fitChindf->SetBinError(fit+1,TMath::Sqrt(2./ndf));
fitNorm->SetBinContent(fit+1,f->GetParameter(0));
fitNorm->SetBinError(fit+1,f->GetParError(0));
fitMu->SetBinContent(fit+1,f->GetParameter(1));
fitMu->SetBinError(fit+1,f->GetParError(1));
fitSigma->SetBinContent(fit+1,f->GetParameter(2));
fitSigma->SetBinError(fit+1,f->GetParError(2));
cout<<"\""<<f->GetName()<<"\","<<r[2]/r[3]<<","<<r[3]
<<","<<TMath::Prob(r[2],r[3])
<<","<<chi2/ndf
<<","<<ndf
<<","<<TMath::Prob(r[0],r[1])
<<","<<r[5];
for(int i=1;i<3;i++) {
cout<<","<<f->GetParameter(i)<<",\"\302\261\","<<f->GetParError(i);
}
cout<<"\n";
}
//=========================== L-curve ==========================
c4->cd(1);
lCurve->SetTitle("L curve;log_{10} L_{x};log_{10} L_{y}");
lCurve->SetLineColor(kRed);
lCurve->Draw("AL");
c4->cd(2);
gPad->Clear();
c4->cd(3);
logTauX->SetTitle(";log_{10} #tau;log_{10} L_{x}");
logTauX->SetLineColor(kBlue);
logTauX->Draw();
c4->cd(4);
logTauY->SetTitle(";log_{10} #tau;log_{10} L_{y}");
logTauY->SetLineColor(kBlue);
logTauY->Draw();
c4->SaveAs("lcurveL.eps");
//========================= rho and L-curve scan ===============
c4->cd(1);
logTauCurvature->SetTitle(";log_{10}(#tau);L curve curvature");
logTauCurvature->SetLineColor(kRed);
logTauCurvature->Draw();
c4->cd(2);
rhoScan->SetTitle(";log_{10}(#tau);average(#rho_{i})");
rhoScan->SetLineColor(kRed);
rhoScan->Draw();
c4->cd(3);
DrawPadTruth(histMcsigGenO,histDataGenO,histOutputFALCurveO,"Tikhonov",tauFA,
&table[iFitFALCurve].second);
c4->cd(4);
DrawPadTruth(histMcsigGenO,histDataGenO,histOutputFArhoO,"Tikhonov",tauFArho,
&table[iFitFArho].second);
c4->SaveAs("scanTau.eps");
TGraph *graphNiterAgoBay[4];
GetNiterGraphs(iAgoFirstFit,iAgoFirstFit+1,table,kRed-2,graphNiterAgoBay,20);
TGraph *graphNiterAgo[4];
GetNiterGraphs(iAgoFirstFit,iAgoLastFit,table,kRed,graphNiterAgo,24);
#ifdef WITH_IDS
TGraph *graphNiterIDS[4];
GetNiterGraphs(iIDSFirstFit,iIDSLastFit,table,kMagenta,graphNiterIDS,21);
#endif
TH1 *histNiterInversion[4];
GetNiterHist(iFitInversion,table,histNiterInversion,kCyan,1,1001);
TH1 *histNiterFALCurve[4];
GetNiterHist(iFitFALCurve,table,histNiterFALCurve,kBlue,2,3353);
TH1 *histNiterFArho[4];
GetNiterHist(iFitFArho,table,histNiterFArho,kAzure-4,3,3353);
TH1 *histNiterBinByBin[4];
GetNiterHist(iFitBinByBin,table,histNiterBinByBin,kOrange+1,3,3335);
histNiterInversion[0]->GetYaxis()->SetRangeUser(0.3,500.);
histNiterInversion[1]->GetYaxis()->SetRangeUser(-0.1,0.9);
histNiterInversion[2]->GetYaxis()->SetRangeUser(5.6,6.3);
histNiterInversion[3]->GetYaxis()->SetRangeUser(1.6,2.4);
TLine *line=0;
c1->cd();
for(int i=0;i<2;i++) {
gPad->Clear();
gPad->SetLogx();
gPad->SetLogy((i<1));
if(! histNiterInversion[i]) continue;
histNiterInversion[i]->Draw("][");
histNiterFALCurve[i]->Draw("SAME ][");
histNiterFArho[i]->Draw("SAME ][");
histNiterBinByBin[i]->Draw("SAME ][");
graphNiterAgo[i]->Draw("LP");
graphNiterAgoBay[i]->SetMarkerStyle(20);
graphNiterAgoBay[i]->Draw("P");
#ifdef WITH_IDS
graphNiterIDS[i]->Draw("LP");
#endif
TLegend *legend;
if(i==1) {
legend=new TLegend(0.48,0.28,0.87,0.63);
} else {
legend=new TLegend(0.45,0.5,0.88,0.88);
}
legend->SetBorderSize(0);
legend->SetFillStyle(1001);
legend->SetFillColor(kWhite);
legend->SetTextSize(kLegendFontSize*0.7);
legend->AddEntry( histNiterInversion[0],"inversion","l");
legend->AddEntry( histNiterFALCurve[0],"Tikhonov L-curve","l");
legend->AddEntry( histNiterFArho[0],"Tikhonov global cor.","l");
legend->AddEntry( histNiterBinByBin[0],"bin-by-bin","l");
legend->AddEntry( graphNiterAgoBay[0],"\"Bayesian\"","p");
legend->AddEntry( graphNiterAgo[0],"iterative","p");
#ifdef WITH_IDS
legend->AddEntry( graphNiterIDS[0],"IDS","p");
#endif
legend->Draw();
c1->SaveAs(TString::Format("niter%d.eps",i));
}
//c4->cd(1);
//DrawPadCorrelations(histRhoFALCurveO,&table);
c2sq->cd(1);
DrawPadTruth(histMcsigGenO,histDataGenO,histOutputFALCurveO,"Tikhonov",tauFA,
&table[iFitFALCurve].second,table[iFitFALCurve].first);
c2sq->cd(2);
gPad->SetLogx();
gPad->SetLogy(false);
histNiterInversion[3]->DrawClone("E2");
histNiterInversion[3]->SetFillStyle(0);
histNiterInversion[3]->Draw("SAME HIST ][");
histNiterFALCurve[3]->DrawClone("SAME E2");
histNiterFALCurve[3]->SetFillStyle(0);
histNiterFALCurve[3]->Draw("SAME HIST ][");
histNiterFArho[3]->DrawClone("SAME E2");
histNiterFArho[3]->SetFillStyle(0);
histNiterFArho[3]->Draw("SAME HIST ][");
histNiterBinByBin[3]->DrawClone("SAME E2");
histNiterBinByBin[3]->SetFillStyle(0);
histNiterBinByBin[3]->Draw("SAME HIST ][");
double yTrue=1.8;
line=new TLine(histNiterInversion[3]->GetXaxis()->GetXmin(),
yTrue,
histNiterInversion[3]->GetXaxis()->GetXmax(),
yTrue);
line->SetLineWidth(3);
line->Draw();
graphNiterAgo[3]->Draw("LP");
graphNiterAgoBay[3]->SetMarkerStyle(20);
graphNiterAgoBay[3]->Draw("P");
#ifdef WITH_IDS
graphNiterIDS[3]->Draw("LP");
#endif
TLegend *legend;
legend=new TLegend(0.55,0.53,0.95,0.97);
legend->SetBorderSize(0);
legend->SetFillStyle(1001);
legend->SetFillColor(kWhite);
legend->SetTextSize(kLegendFontSize);
legend->AddEntry( line,"truth","l");
legend->AddEntry( histNiterInversion[3],"inversion","l");
legend->AddEntry( histNiterFALCurve[3],"Tikhonov L-curve","l");
legend->AddEntry( histNiterFArho[3],"Tikhonov global cor.","l");
legend->AddEntry( histNiterBinByBin[3],"bin-by-bin","l");
legend->AddEntry( graphNiterAgoBay[3],"\"Bayesian\"","p");
legend->AddEntry( graphNiterAgo[3],"iterative","p");
#ifdef WITH_IDS
legend->AddEntry( graphNiterIDS[3],"IDS","p");
#endif
legend->Draw();
c2sq->SaveAs("fitSigma.eps");
outputFile->Write();
delete outputFile;
}
void GetNiterGraphs(int iFirst,int iLast,vector<pair<TF1*,
vector<double> > > const &table,int color,
TGraph *graph[4],int style) {
TVectorD niter(iLast-iFirst);
TVectorD eniter(iLast-iFirst);
TVectorD chi2(iLast-iFirst);
TVectorD gcor(iLast-iFirst);
TVectorD mean(iLast-iFirst);
TVectorD emean(iLast-iFirst);
TVectorD sigma(iLast-iFirst);
TVectorD esigma(iLast-iFirst);
for(int ifit=iFirst;ifit<iLast;ifit++) {
vector<double> const &r=table[ifit].second;
niter(ifit-iFirst)=r[4];
chi2(ifit-iFirst)=r[2]/r[3];
gcor(ifit-iFirst)=r[5];
TF1 const *f=table[ifit].first;
mean(ifit-iFirst)=f->GetParameter(1);
emean(ifit-iFirst)=f->GetParError(1);
sigma(ifit-iFirst)=f->GetParameter(2);
esigma(ifit-iFirst)=f->GetParError(2);
}
graph[0]=new TGraph(niter,chi2);
graph[1]=new TGraph(niter,gcor);
graph[2]=new TGraphErrors(niter,mean,eniter,emean);
graph[3]=new TGraphErrors(niter,sigma,eniter,esigma);
for(int g=0;g<4;g++) {
if(graph[g]) {
graph[g]->SetLineColor(color);
graph[g]->SetMarkerColor(color);
graph[g]->SetMarkerStyle(style);
}
}
}
void GetNiterHist(int ifit,vector<pair<TF1*,vector<double> > > const &table,
TH1 *hist[4],int color,int style,int fillStyle) {
vector<double> const &r=table[ifit].second;
TF1 const *f=table[ifit].first;
hist[0]=new TH1D(table[ifit].first->GetName()+TString("_chi2"),
";iteration;unfold-truth #chi^{2}/N_{D.F.}",1,0.2,1500.);
hist[0]->SetBinContent(1,r[2]/r[3]);
hist[1]=new TH1D(table[ifit].first->GetName()+TString("_gcor"),
";iteration;avg(#rho_{i})",1,0.2,1500.);
hist[1]->SetBinContent(1,r[5]);
hist[2]=new TH1D(table[ifit].first->GetName()+TString("_mu"),
";iteration;parameter #mu",1,0.2,1500.);
hist[2]->SetBinContent(1,f->GetParameter(1));
hist[2]->SetBinError(1,f->GetParError(1));
hist[3]=new TH1D(table[ifit].first->GetName()+TString("_sigma"),
";iteration;parameter #sigma",1,0.2,1500.);
hist[3]->SetBinContent(1,f->GetParameter(2));
hist[3]->SetBinError(1,f->GetParError(2));
for(int h=0;h<4;h++) {
if(hist[h]) {
hist[h]->SetLineColor(color);
hist[h]->SetLineStyle(style);
if( hist[h]->GetBinError(1)>0.0) {
hist[h]->SetFillColor(color-10);
hist[h]->SetFillStyle(fillStyle);
}
hist[h]->SetMarkerStyle(0);
}
}
}
void CreateHistogramCopies(TH1 *h[3],TUnfoldBinning const *binning) {
TString baseName(h[0]->GetName());
Int_t *binMap;
h[1]=binning->CreateHistogram(baseName+"_axis",kTRUE,&binMap);
h[2]=(TH1 *)h[1]->Clone(baseName+"_binw");
Int_t nMax=binning->GetEndBin()+1;
for(Int_t iSrc=0;iSrc<nMax;iSrc++) {
Int_t iDest=binMap[iSrc];
double c=h[0]->GetBinContent(iSrc)+h[1]->GetBinContent(iDest);
double e=TMath::Hypot(h[0]->GetBinError(iSrc),h[1]->GetBinError(iDest));
h[1]->SetBinContent(iDest,c);
h[1]->SetBinError(iDest,e);
h[2]->SetBinContent(iDest,c);
h[2]->SetBinError(iDest,e);
}
for(int iDest=0;iDest<=h[2]->GetNbinsX()+1;iDest++) {
double c=h[2]->GetBinContent(iDest);
double e=h[2]->GetBinError(iDest);
double bw=binning->GetBinSize(iDest);
/* if(bw!=h[2]->GetBinWidth(iDest)) {
cout<<"bin "<<iDest<<" width="<<bw<<" "<<h[2]->GetBinWidth(iDest)
<<"\n";
} */
if(bw>0.0) {
h[2]->SetBinContent(iDest,c/bw);
h[2]->SetBinError(iDest,e/bw);
} else {
}
}
}
void CreateHistogramCopies(TH2 *h[3],TUnfoldBinning const *binningX) {
h[1]=0;
h[2]=0;
}
TH2 *AddOverflowXY(TH2 *h,double widthX,double widthY) {
// add overflow bin to X-axis
int nx=h->GetNbinsX();
int ny=h->GetNbinsY();
double *xBins=new double[nx+2];
double *yBins=new double[ny+2];
for(int i=1;i<=nx;i++) {
xBins[i-1]=h->GetXaxis()->GetBinLowEdge(i);
}
xBins[nx]=h->GetXaxis()->GetBinUpEdge(nx);
xBins[nx+1]=xBins[nx]+widthX;
for(int i=1;i<=ny;i++) {
yBins[i-1]=h->GetYaxis()->GetBinLowEdge(i);
}
yBins[ny]=h->GetYaxis()->GetBinUpEdge(ny);
yBins[ny+1]=yBins[ny]+widthY;
TString name(h->GetName());
name+="U";
TH2 *r=new TH2D(name,h->GetTitle(),nx+1,xBins,ny+1,yBins);
for(int ix=0;ix<=nx+1;ix++) {
for(int iy=0;iy<=ny+1;iy++) {
r->SetBinContent(ix,iy,h->GetBinContent(ix,iy));
r->SetBinError(ix,iy,h->GetBinError(ix,iy));
}
}
delete [] yBins;
delete [] xBins;
return r;
}
TH1 *AddOverflowX(TH1 *h,double widthX) {
// add overflow bin to X-axis
int nx=h->GetNbinsX();
double *xBins=new double[nx+2];
for(int i=1;i<=nx;i++) {
xBins[i-1]=h->GetXaxis()->GetBinLowEdge(i);
}
xBins[nx]=h->GetXaxis()->GetBinUpEdge(nx);
xBins[nx+1]=xBins[nx]+widthX;
TString name(h->GetName());
name+="U";
TH1 *r=new TH1D(name,h->GetTitle(),nx+1,xBins);
for(int ix=0;ix<=nx+1;ix++) {
r->SetBinContent(ix,h->GetBinContent(ix));
r->SetBinError(ix,h->GetBinError(ix));
}
delete [] xBins;
return r;
}
void DrawOverflowX(TH1 *h,double posy) {
double x1=h->GetXaxis()->GetBinLowEdge(h->GetNbinsX());
double x2=h->GetXaxis()->GetBinUpEdge(h->GetNbinsX());
double y0=h->GetYaxis()->GetBinLowEdge(1);
double y2=h->GetYaxis()->GetBinUpEdge(h->GetNbinsY());;
if(h->GetDimension()==1) {
y0=h->GetMinimum();
y2=h->GetMaximum();
}
double w1=-0.3;
TText *textX=new TText((1.+w1)*x2-w1*x1,(1.-posy)*y0+posy*y2,"Overflow bin");
textX->SetNDC(kFALSE);
textX->SetTextSize(0.05);
textX->SetTextAngle(90.);
textX->Draw();
TLine *lineX=new TLine(x1,y0,x1,y2);
lineX->Draw();
}
void DrawOverflowY(TH1 *h,double posx) {
double x0=h->GetXaxis()->GetBinLowEdge(1);
double x2=h->GetXaxis()->GetBinUpEdge(h->GetNbinsX());
double y1=h->GetYaxis()->GetBinLowEdge(h->GetNbinsY());;
double y2=h->GetYaxis()->GetBinUpEdge(h->GetNbinsY());;
double w1=-0.3;
TText *textY=new TText((1.-posx)*x0+posx*x2,(1.+w1)*y1-w1*y2,"Overflow bin");
textY->SetNDC(kFALSE);
textY->SetTextSize(0.05);
textY->Draw();
TLine *lineY=new TLine(x0,y1,x2,y1);
lineY->Draw();
}
void DrawPadProbability(TH2 *h) {
h->Draw("COLZ");
h->SetTitle("migration probabilities;P_{T}(gen) [GeV];P_{T}(rec) [GeV]");
DrawOverflowX(h,0.05);
DrawOverflowY(h,0.35);
}
void DrawPadEfficiency(TH1 *h) {
h->SetTitle("efficiency;P_{T}(gen) [GeV];#epsilon");
h->SetLineColor(kBlue);
h->SetMinimum(0.75);
h->SetMaximum(1.0);
h->Draw();
DrawOverflowX(h,0.05);
TLegend *legEfficiency=new TLegend(0.3,0.58,0.6,0.75);
legEfficiency->SetBorderSize(0);
legEfficiency->SetFillStyle(0);
legEfficiency->SetTextSize(kLegendFontSize);
legEfficiency->AddEntry(h,"reconstruction","l");
legEfficiency->AddEntry((TObject*)0," efficiency","");
legEfficiency->Draw();
}
void DrawPadReco(TH1 *histMcRec,TH1 *histMcbgrRec,TH1 *histDataRec,
TH1 *histDataUnfold,TH2 *histProbability,TH2 *histRhoij) {
//gPad->SetLogy(kTRUE);
double amax=0.0;
for(int i=1;i<=histMcRec->GetNbinsX();i++) {
amax=TMath::Max(amax,histMcRec->GetBinContent(i)
+5.0*histMcRec->GetBinError(i));
amax=TMath::Max(amax,histDataRec->GetBinContent(i)
+2.0*histDataRec->GetBinError(i));
}
histMcRec->SetTitle("Reconstructed;P_{T}(rec);Nevent / GeV");
histMcRec->Draw("HIST");
histMcRec->SetLineColor(kBlue);
histMcRec->SetMinimum(1.0);
histMcRec->SetMaximum(amax);
//histMcbgrRec->SetFillMode(1);
histMcbgrRec->SetLineColor(kBlue-6);
histMcbgrRec->SetFillColor(kBlue-10);
histMcbgrRec->Draw("SAME HIST");
TH1 * histFoldBack=0;
if(histDataUnfold && histProbability && histRhoij) {
histFoldBack=(TH1 *)
histMcRec->Clone(histDataUnfold->GetName()+TString("_folded"));
int nrec=histFoldBack->GetNbinsX();
if((nrec==histProbability->GetNbinsY())&&
(nrec==histMcbgrRec->GetNbinsX())&&
(nrec==histDataRec->GetNbinsX())
) {
for(int ix=1;ix<=nrec;ix++) {
double sum=0.0;
double sume2=0.0;
for(int iy=0;iy<=histProbability->GetNbinsX()+1;iy++) {
sum += histDataUnfold->GetBinContent(iy)*
histDataUnfold->GetBinWidth(iy)*
histProbability->GetBinContent(iy,ix);
for(int iy2=0;iy2<=histProbability->GetNbinsX()+1;iy2++) {
sume2 += histDataUnfold->GetBinError(iy)*
histDataUnfold->GetBinWidth(iy)*
histProbability->GetBinContent(iy,ix)*
histDataUnfold->GetBinError(iy2)*
histDataUnfold->GetBinWidth(iy2)*
histProbability->GetBinContent(iy2,ix)*
histRhoij->GetBinContent(iy,iy2);
}
}
sum /= histFoldBack->GetBinWidth(ix);
sum += histMcbgrRec->GetBinContent(ix);
histFoldBack->SetBinContent(ix,sum);
histFoldBack->SetBinError(ix,TMath::Sqrt(sume2)
/histFoldBack->GetBinWidth(ix));
}
} else {
cout<<"can not fold back: "<<nrec
<<" "<<histProbability->GetNbinsY()
<<" "<<histMcbgrRec->GetNbinsX()
<<" "<<histDataRec->GetNbinsX()
<<"\n";
exit(0);
}
histFoldBack->SetLineColor(kBlack);
histFoldBack->SetMarkerStyle(0);
histFoldBack->Draw("SAME HIST");
}
histDataRec->SetLineColor(kRed);
histDataRec->SetMarkerColor(kRed);
histDataRec->Draw("SAME");
DrawOverflowX(histMcRec,0.5);
TLegend *legRec=new TLegend(0.4,0.5,0.68,0.85);
legRec->SetBorderSize(0);
legRec->SetFillStyle(0);
legRec->SetTextSize(kLegendFontSize);
legRec->AddEntry(histMcRec,"MC total","l");
legRec->AddEntry(histMcbgrRec,"background","f");
if(histFoldBack) {
int ndf=-kNbinC;
double sumD=0.,sumF=0.,chi2=0.;
for(int i=1;i<=histDataRec->GetNbinsX();i++) {
//cout<<histDataRec->GetBinContent(i)<<" "<<histFoldBack->GetBinContent(i)<<" "<<" w="<<histFoldBack->GetBinWidth(i)<<"\n";
sumD+=histDataRec->GetBinContent(i)*histDataRec->GetBinWidth(i);
sumF+=histFoldBack->GetBinContent(i)*histFoldBack->GetBinWidth(i);
double pull=(histFoldBack->GetBinContent(i)-histDataRec->GetBinContent(i))/histDataRec->GetBinError(i);
chi2+= pull*pull;
ndf+=1;
}
legRec->AddEntry(histDataRec,TString::Format("data N_{evt}=%.0f",sumD),"lp");
legRec->AddEntry(histFoldBack,TString::Format("folded N_{evt}=%.0f",sumF),"l");
legRec->AddEntry((TObject*)0,TString::Format("#chi^{2}=%.1f ndf=%d",chi2,ndf),"");
//exit(0);
} else {
legRec->AddEntry(histDataRec,"data","lp");
}
legRec->Draw();
}
void DrawPadTruth(TH1 *histMcsigGen,TH1 *histDataGen,TH1 *histDataUnfold,
char const *text,double tau,vector<double> const *r,
TF1 *f) {
//gPad->SetLogy(kTRUE);
double amin=0.;
double amax=0.;
for(int i=1;i<=histMcsigGen->GetNbinsX();i++) {
if(histDataUnfold) {
amin=TMath::Min(amin,histDataUnfold->GetBinContent(i)
-1.1*histDataUnfold->GetBinError(i));
amax=TMath::Max(amax,histDataUnfold->GetBinContent(i)
+1.1*histDataUnfold->GetBinError(i));
}
amin=TMath::Min(amin,histMcsigGen->GetBinContent(i)
-histMcsigGen->GetBinError(i));
amin=TMath::Min(amin,histDataGen->GetBinContent(i)
-histDataGen->GetBinError(i));
amax=TMath::Max(amax,histMcsigGen->GetBinContent(i)
+10.*histMcsigGen->GetBinError(i));
amax=TMath::Max(amax,histDataGen->GetBinContent(i)
+2.*histDataGen->GetBinError(i));
}
histMcsigGen->SetMinimum(amin);
histMcsigGen->SetMaximum(amax);
histMcsigGen->SetTitle("Truth;P_{T};Nevent / GeV");
histMcsigGen->SetLineColor(kBlue);
histMcsigGen->Draw("HIST");
histDataGen->SetLineColor(kRed);
histDataGen->SetMarkerColor(kRed);
histDataGen->SetMarkerSize(1.0);
histDataGen->Draw("SAME HIST");
if(histDataUnfold) {
histDataUnfold->SetMarkerStyle(21);
histDataUnfold->SetMarkerSize(0.7);
histDataUnfold->Draw("SAME");
}
DrawOverflowX(histMcsigGen,0.5);
if(f) {
f->SetLineStyle(1);
f->Draw("SAME");
}
TLegend *legTruth=new TLegend(0.32,0.65,0.6,0.9);
legTruth->SetBorderSize(0);
legTruth->SetFillStyle(0);
legTruth->SetTextSize(kLegendFontSize);
legTruth->AddEntry(histMcsigGen,"MC","l");
if(!histDataUnfold) legTruth->AddEntry((TObject *)0," Landau(5,2)","");
legTruth->AddEntry(histDataGen,"data","l");
if(!histDataUnfold) legTruth->AddEntry((TObject *)0," Landau(6,1.8)","");
if(histDataUnfold) {
TString t;
if(text) t=text;
else t=histDataUnfold->GetName();
if(tau>0) {
t+=TString::Format(" #tau=%.2g",tau);
}
legTruth->AddEntry(histDataUnfold,t,"lp");
if(r) {
legTruth->AddEntry((TObject *)0,"test wrt data:","");
legTruth->AddEntry((TObject *)0,TString::Format
("#chi^{2}/%d=%.1f prob=%.3f",
(int)(*r)[3],(*r)[2]/(*r)[3],
TMath::Prob((*r)[2],(*r)[3])),"");
}
}
if(f) {
legTruth->AddEntry(f,"fit","l");
}
legTruth->Draw();
if(histDataUnfold ) {
TPad *subpad = new TPad("subpad","",0.35,0.29,0.88,0.68);
subpad->SetFillStyle(0);
subpad->Draw();
subpad->cd();
amin=0.;
amax=0.;
int istart=11;
for(int i=istart;i<=histMcsigGen->GetNbinsX();i++) {
amin=TMath::Min(amin,histMcsigGen->GetBinContent(i)
-histMcsigGen->GetBinError(i));
amin=TMath::Min(amin,histDataGen->GetBinContent(i)
-histDataGen->GetBinError(i));
amin=TMath::Min(amin,histDataUnfold->GetBinContent(i)
-histDataUnfold->GetBinError(i));
amax=TMath::Max(amax,histMcsigGen->GetBinContent(i)
+histMcsigGen->GetBinError(i));
amax=TMath::Max(amax,histDataGen->GetBinContent(i)
+histDataGen->GetBinError(i));
amax=TMath::Max(amax,histDataUnfold->GetBinContent(i)
+histDataUnfold->GetBinError(i));
}
TH1 *copyMcsigGen=(TH1*)histMcsigGen->Clone();
TH1 *copyDataGen=(TH1*)histDataGen->Clone();
TH1 *copyDataUnfold=(TH1*)histDataUnfold->Clone();
copyMcsigGen->GetXaxis()->SetRangeUser
(copyMcsigGen->GetXaxis()->GetBinLowEdge(istart),
copyMcsigGen->GetXaxis()->GetBinUpEdge(copyMcsigGen->GetNbinsX()-1));
copyMcsigGen->SetTitle(";;");
copyMcsigGen->GetYaxis()->SetRangeUser(amin,amax);
copyMcsigGen->Draw("HIST");
copyDataGen->Draw("SAME HIST");
copyDataUnfold->Draw("SAME");
if(f) {
((TF1 *)f->Clone())->Draw("SAME");
}
}
}
void DrawPadCorrelations(TH2 *h,
vector<pair<TF1*,vector<double> > > const *table) {
h->SetMinimum(-1.);
h->SetMaximum(1.);
h->SetTitle("correlation coefficients;P_{T}(gen) [GeV];P_{T}(gen) [GeV]");
h->Draw("COLZ");
DrawOverflowX(h,0.05);
DrawOverflowY(h,0.05);
if(table) {
TLegend *legGCor=new TLegend(0.13,0.6,0.5,0.8);
legGCor->SetBorderSize(0);
legGCor->SetFillStyle(0);
legGCor->SetTextSize(kLegendFontSize);
vector<double> const &r=(*table)[table->size()-1].second;
legGCor->AddEntry((TObject *)0,TString::Format("min(#rho_{ij})=%5.2f",r[6]),"");
legGCor->AddEntry((TObject *)0,TString::Format("max(#rho_{ij})=%5.2f",r[7]),"");
legGCor->AddEntry((TObject *)0,TString::Format("avg(#rho_i)=%5.2f",r[5]),"");
legGCor->Draw();
}
}
TH1 *g_fcnHist=0;
TMatrixD *g_fcnMatrix=0;
void fcn(Int_t &npar, Double_t *gin, Double_t &f, Double_t *u, Int_t flag) {
if(flag==0) {
cout<<"fcn flag=0: npar="<<npar<<" gin="<<gin<<" par=[";
for(int i=0;i<npar;i++) {
cout<<" "<<u[i];
}
cout<<"]\n";
}
int n=g_fcnMatrix->GetNrows();
TVectorD dy(n);
double x0=0,y0=0.;
for(int i=0;i<=n;i++) {
double x1;
if(i<1) x1=g_fcnHist->GetXaxis()->GetBinLowEdge(i+1);
else x1=g_fcnHist->GetXaxis()->GetBinUpEdge(i);
double y1=TMath::LandauI((x1-u[1])/u[2]);
if(i>0) {
double iy=u[0]*u[2]*(y1-y0)/(x1-x0);
dy(i-1)=iy-g_fcnHist->GetBinContent(i);
//cout<<"i="<<i<<" iy="<<iy<<" delta="<< dy(i-1)<<"\n";
}
x0=x1;
y0=y1;
//cout<<"i="<<i<<" y1="<<y1<<" x1="<<x1<<"\n";
}
TVectorD Hdy=(*g_fcnMatrix) * dy;
//Hdy.Print();
f=Hdy*dy;
//exit(0);
}
TFitResultPtr DoFit(TH1 *h,TH2 *rho,TH1 *truth,const char *text,
vector<pair<TF1 *,vector<double> > > &table,int niter) {
TString option="IESN";
cout<<h->GetName()<<"\n";
double gcorAvg=0.;
double rhoMin=0.;
double rhoMax=0.;
if(rho) {
g_fcnHist=h;
int n=h->GetNbinsX()-1; // overflow is included as extra bin, exclude in fit
TMatrixDSym v(n);
//g_fcnMatrix=new TMatrixD(n,n);
for(int i=0;i<n;i++) {
for(int j=0;j<n;j++) {
v(i,j)=rho->GetBinContent(i+1,j+1)*
(h->GetBinError(i+1)*h->GetBinError(j+1));
}
}
TMatrixDSymEigen ev(v);
TMatrixD d(n,n);
TVectorD di(ev.GetEigenValues());
for(int i=0;i<n;i++) {
if(di(i)>0.0) {
d(i,i)=1./di(i);
} else {
cout<<"bad eigenvalue i="<<i<<" di="<<di(i)<<"\n";
exit(0);
}
}
TMatrixD O(ev.GetEigenVectors());
TMatrixD DOT(d,TMatrixD::kMultTranspose,O);
g_fcnMatrix=new TMatrixD(O,TMatrixD::kMult,DOT);
TMatrixD test(*g_fcnMatrix,TMatrixD::kMult,v);
int error=0;
for(int i=0;i<n;i++) {
if(TMath::Abs(test(i,i)-1.0)>1.E-7) {
error++;
}
for(int j=0;j<n;j++) {
if(i==j) continue;
if(TMath::Abs(test(i,j)>1.E-7)) error++;
}
}
// calculate global correlation coefficient (all bins)
TMatrixDSym v1(n+1);
rhoMin=1.;
rhoMax=-1.;
for(int i=0;i<=n;i++) {
for(int j=0;j<=n;j++) {
double rho_ij=rho->GetBinContent(i+1,j+1);
v1(i,j)=rho_ij*
(h->GetBinError(i+1)*h->GetBinError(j+1));
if(i!=j) {
if(rho_ij<rhoMin) rhoMin=rho_ij;
if(rho_ij>rhoMax) rhoMax=rho_ij;
}
}
}
TMatrixDSymEigen ev1(v1);
TMatrixD d1(n+1,n+1);
TVectorD di1(ev1.GetEigenValues());
for(int i=0;i<=n;i++) {
if(di1(i)>0.0) {
d1(i,i)=1./di1(i);
} else {
cout<<"bad eigenvalue i="<<i<<" di1="<<di1(i)<<"\n";
exit(0);
}
}
TMatrixD O1(ev1.GetEigenVectors());
TMatrixD DOT1(d1,TMatrixD::kMultTranspose,O1);
TMatrixD vinv1(O1,TMatrixD::kMult,DOT1);
for(int i=0;i<=n;i++) {
double gcor2=1.-1./(vinv1(i,i)*v1(i,i));
if(gcor2>=0.0) {
double gcor=TMath::Sqrt(gcor2);
gcorAvg += gcor;
} else {
cout<<"bad global correlation "<<i<<" "<<gcor2<<"\n";
}
}
gcorAvg /=(n+1);
/* if(error) {
v.Print();
g_fcnMatrix->Print();
exit(0);
} */
//g_fcnMatrix->Invert();
//from: HFitImpl.cxx
// TVirtualFitter::FCNFunc_t userFcn = 0;
// typedef void (* FCNFunc_t )(Int_t &npar, Double_t *gin, Double_t &f, Double_t *u, Int_t flag);
// userFcn = (TVirtualFitter::GetFitter())->GetFCN();
// (TVirtualFitter::GetFitter())->SetUserFunc(f1);
//...
//fitok = fitter->FitFCN( userFcn );
TVirtualFitter::Fitter(h)->SetFCN(fcn);
option += "U";
}
double xmax=h->GetXaxis()->GetBinUpEdge(h->GetNbinsX()-1);
TF1 *landau=new TF1(text,"[0]*TMath::Landau(x,[1],[2],0)",
0.,xmax);
landau->SetParameter(0,6000.);
landau->SetParameter(1,5.);
landau->SetParameter(2,2.);
landau->SetParError(0,10.);
landau->SetParError(1,0.5);
landau->SetParError(2,0.1);
TFitResultPtr s=h->Fit(landau,option,0,0.,xmax);
vector<double> r(8);
int np=landau->GetNpar();
fcn(np,0,r[0],landau->GetParameters(),0);
r[1]=h->GetNbinsX()-1-landau->GetNpar();
for(int i=0;i<h->GetNbinsX()-1;i++) {
double di=h->GetBinContent(i+1)-truth->GetBinContent(i+1);
if(g_fcnMatrix) {
for(int j=0;j<h->GetNbinsX()-1;j++) {
double dj=h->GetBinContent(j+1)-truth->GetBinContent(j+1);
r[2]+=di*dj*(*g_fcnMatrix)(i,j);
}
} else {
double pull=di/h->GetBinError(i+1);
r[2]+=pull*pull;
}
r[3]+=1.0;
}
r[4]=niter;
if(!niter) r[4]=0.25;
r[5]=gcorAvg;
r[6]=rhoMin;
r[7]=rhoMax;
if(rho) {
g_fcnHist=0;
delete g_fcnMatrix;
g_fcnMatrix=0;
}
table.push_back(make_pair(landau,r));
return s;
}
#ifdef WITH_IDS
//===================== interface to IDS unfolding code follows here
// contact Bogdan Malescu to find it
#include "ids_code.cc"
void IDSfirst(TVectorD *data, TVectorD *dataErr, TMatrixD *A_, Double_t lambdaL_, TVectorD* &unfres1IDS_,TVectorD *&soustr){
int N_=data->GetNrows();
soustr = new TVectorD(N_);
for( Int_t i=0; i<N_; i++ ){ (*soustr)[i] = 0.; }
unfres1IDS_ = Unfold( data, dataErr, A_, N_, lambdaL_, soustr );
}
void IDSiterate(TVectorD *data, TVectorD *dataErr, TMatrixD *A_, TMatrixD *Am_, Double_t lambdaU_, Double_t lambdaM_, Double_t lambdaS_,TVectorD* &unfres2IDS_ ,TVectorD *&soustr) {
int N_=data->GetNrows();
ModifyMatrix( Am_, A_, unfres2IDS_, dataErr, N_, lambdaM_, soustr, lambdaS_ );
delete unfres2IDS_;
unfres2IDS_ = Unfold( data, dataErr, Am_, N_, lambdaU_, soustr );
}
#endif
r
ROOT::R::TRInterface & r
Definition: Object.C:4
d
#define d(i)
Definition: RSha256.hxx:102
b
#define b(i)
Definition: RSha256.hxx:100
f
#define f(i)
Definition: RSha256.hxx:104
c
#define c(i)
Definition: RSha256.hxx:101
g
#define g(i)
Definition: RSha256.hxx:105
h
#define h(i)
Definition: RSha256.hxx:106
e
#define e(i)
Definition: RSha256.hxx:103
x2
static const double x2[5]
Definition: RooGaussKronrodIntegrator1D.cxx:364
x1
static const double x1[5]
Definition: RooGaussKronrodIntegrator1D.cxx:346
Int_t
int Int_t
Definition: RtypesCore.h:41
kFALSE
const Bool_t kFALSE
Definition: RtypesCore.h:88
Double_t
double Double_t
Definition: RtypesCore.h:55
kTRUE
const Bool_t kTRUE
Definition: RtypesCore.h:87
kRed
@ kRed
Definition: Rtypes.h:64
kOrange
@ kOrange
Definition: Rtypes.h:65
kBlack
@ kBlack
Definition: Rtypes.h:63
kMagenta
@ kMagenta
Definition: Rtypes.h:64
kWhite
@ kWhite
Definition: Rtypes.h:63
kCyan
@ kCyan
Definition: Rtypes.h:64
kBlue
@ kBlue
Definition: Rtypes.h:64
kAzure
@ kAzure
Definition: Rtypes.h:65
width
include TDocParser_001 C image html pict1_TDocParser_001 png width
Definition: TDocParser.cxx:121
gErrorIgnoreLevel
R__EXTERN Int_t gErrorIgnoreLevel
Definition: TError.h:105
kInfo
const Int_t kInfo
Definition: TError.h:37
name
char name[80]
Definition: TGX11.cxx:109
xmax
float xmax
Definition: THbookFile.cxx:93
TMatrixD
TMatrixT< Double_t > TMatrixD
Definition: TMatrixDfwd.h:22
gStyle
R__EXTERN TStyle * gStyle
Definition: TStyle.h:407
TVectorD
TVectorT< Double_t > TVectorD
Definition: TVectorDfwd.h:22
gPad
#define gPad
Definition: TVirtualPad.h:286
TAttFill::SetFillColor
virtual void SetFillColor(Color_t fcolor)
Set the fill area color.
Definition: TAttFill.h:37
TAttFill::SetFillStyle
virtual void SetFillStyle(Style_t fstyle)
Set the fill area style.
Definition: TAttFill.h:39
TAttLine::SetLineStyle
virtual void SetLineStyle(Style_t lstyle)
Set the line style.
Definition: TAttLine.h:42
TAttLine::SetLineWidth
virtual void SetLineWidth(Width_t lwidth)
Set the line width.
Definition: TAttLine.h:43
TAttLine::SetLineColor
virtual void SetLineColor(Color_t lcolor)
Set the line color.
Definition: TAttLine.h:40
TAttMarker::SetMarkerColor
virtual void SetMarkerColor(Color_t mcolor=1)
Set the marker color.
Definition: TAttMarker.h:38
TAttMarker::SetMarkerStyle
virtual void SetMarkerStyle(Style_t mstyle=1)
Set the marker style.
Definition: TAttMarker.h:40
TAttMarker::SetMarkerSize
virtual void SetMarkerSize(Size_t msize=1)
Set the marker size.
Definition: TAttMarker.h:41
TAttText::SetTextAngle
virtual void SetTextAngle(Float_t tangle=0)
Set the text angle.
Definition: TAttText.h:42
TAttText::SetTextSize
virtual void SetTextSize(Float_t tsize=1)
Set the text size.
Definition: TAttText.h:46
TAxis::SetBinLabel
virtual void SetBinLabel(Int_t bin, const char *label)
Set label for bin.
Definition: TAxis.cxx:809
TAxis::GetBinLowEdge
virtual Double_t GetBinLowEdge(Int_t bin) const
Return low edge of bin.
Definition: TAxis.cxx:504
TAxis::SetRangeUser
virtual void SetRangeUser(Double_t ufirst, Double_t ulast)
Set the viewing range for the axis from ufirst to ulast (in user coordinates).
Definition: TAxis.cxx:928
TAxis::GetBinWidth
virtual Double_t GetBinWidth(Int_t bin) const
Return bin width.
Definition: TAxis.cxx:526
TAxis::GetBinUpEdge
virtual Double_t GetBinUpEdge(Int_t bin) const
Return up edge of bin.
Definition: TAxis.cxx:514
TCanvas
The Canvas class.
Definition: TCanvas.h:31
TCanvas::cd
TVirtualPad * cd(Int_t subpadnumber=0)
Set current canvas & pad.
Definition: TCanvas.cxx:696
TDirectoryFile::cd
Bool_t cd(const char *path=nullptr) override
Change current directory to "this" directory.
Definition: TDirectoryFile.cxx:339
TDirectory::GetObject
void GetObject(const char *namecycle, T *&ptr)
Definition: TDirectory.h:149
TF1
1-Dim function class
Definition: TF1.h:211
TF1::SetParError
virtual void SetParError(Int_t ipar, Double_t error)
Set error for parameter number ipar.
Definition: TF1.cxx:3472
TF1::GetNpar
virtual Int_t GetNpar() const
Definition: TF1.h:475
TF1::GetParameters
virtual Double_t * GetParameters() const
Definition: TF1.h:514
TF1::SetParameter
virtual void SetParameter(Int_t param, Double_t value)
Definition: TF1.h:628
TFile
A ROOT file is a suite of consecutive data records (TKey instances) with a well defined format.
Definition: TFile.h:48
TFile::Write
Int_t Write(const char *name=nullptr, Int_t opt=0, Int_t bufsiz=0) override
Write memory objects to this file.
Definition: TFile.cxx:2277
TFitResultPtr
Provides an indirection to the TFitResult class and with a semantics identical to a TFitResult pointe...
Definition: TFitResultPtr.h:31
TGraphErrors
A TGraphErrors is a TGraph with error bars.
Definition: TGraphErrors.h:26
TGraph
A Graph is a graphics object made of two arrays X and Y with npoints each.
Definition: TGraph.h:41
TGraph::SetTitle
virtual void SetTitle(const char *title="")
Change (i.e.
Definition: TGraph.cxx:2312
TGraph::Draw
virtual void Draw(Option_t *chopt="")
Draw this graph with its current attributes.
Definition: TGraph.cxx:753
TH1D
1-D histogram with a double per channel (see TH1 documentation)}
Definition: TH1.h:614
TH1
The TH1 histogram class.
Definition: TH1.h:56
TH1::SetTitle
virtual void SetTitle(const char *title)
See GetStatOverflows for more information.
Definition: TH1.cxx:6333
TH1::Multiply
virtual Bool_t Multiply(TF1 *f1, Double_t c1=1)
Performs the operation:
Definition: TH1.cxx:5650
TH1::GetNbinsY
virtual Int_t GetNbinsY() const
Definition: TH1.h:293
TH1::GetBinError
virtual Double_t GetBinError(Int_t bin) const
Return value of error associated to bin number bin.
Definition: TH1.cxx:8507
TH1::GetXaxis
TAxis * GetXaxis()
Get the behaviour adopted by the object about the statoverflows. See EStatOverflows for more informat...
Definition: TH1.h:316
TH1::Clone
TObject * Clone(const char *newname=0) const
Make a complete copy of the underlying object.
Definition: TH1.cxx:2665
TH1::GetNbinsX
virtual Int_t GetNbinsX() const
Definition: TH1.h:292
TH1::SetMaximum
virtual void SetMaximum(Double_t maximum=-1111)
Definition: TH1.h:394
TH1::Add
virtual Bool_t Add(TF1 *h1, Double_t c1=1, Option_t *option="")
Performs the operation: this = this + c1*f1 if errors are defined (see TH1::Sumw2),...
Definition: TH1.cxx:778
TH1::SetBinError
virtual void SetBinError(Int_t bin, Double_t error)
Set the bin Error Note that this resets the bin eror option to be of Normal Type and for the non-empt...
Definition: TH1.cxx:8650
TH1::GetYaxis
TAxis * GetYaxis()
Definition: TH1.h:317
TH1::SetMinimum
virtual void SetMinimum(Double_t minimum=-1111)
Definition: TH1.h:395
TH1::SetDefaultSumw2
static void SetDefaultSumw2(Bool_t sumw2=kTRUE)
When this static function is called with sumw2=kTRUE, all new histograms will automatically activate ...
Definition: TH1.cxx:6318
TH1::SetBinContent
virtual void SetBinContent(Int_t bin, Double_t content)
Set bin content see convention for numbering bins in TH1::GetBin In case the bin number is greater th...
Definition: TH1.cxx:8666
TH1::Draw
virtual void Draw(Option_t *option="")
Draw this histogram with options.
Definition: TH1.cxx:2998
TH1::GetBinContent
virtual Double_t GetBinContent(Int_t bin) const
Return content of bin number bin.
Definition: TH1.cxx:4899
TH1::GetBinWidth
virtual Double_t GetBinWidth(Int_t bin) const
Return bin width for 1D histogram.
Definition: TH1.cxx:8607
TH1::Scale
virtual void Scale(Double_t c1=1, Option_t *option="")
Multiply this histogram by a constant c1.
Definition: TH1.cxx:6234
TH1::Divide
virtual Bool_t Divide(TF1 *f1, Double_t c1=1)
Performs the operation: this = this/(c1*f1) if errors are defined (see TH1::Sumw2),...
Definition: TH1.cxx:2753
TH2D
2-D histogram with a double per channel (see TH1 documentation)}
Definition: TH2.h:292
TH2
Service class for 2-Dim histogram classes.
Definition: TH2.h:30
TH2::ProjectionX
TH1D * ProjectionX(const char *name="_px", Int_t firstybin=0, Int_t lastybin=-1, Option_t *option="") const
Project a 2-D histogram into a 1-D histogram along X.
Definition: TH2.cxx:2261
TH2::GetBinContent
virtual Double_t GetBinContent(Int_t bin) const
Return content of bin number bin.
Definition: TH2.h:88
TH2::SetBinContent
virtual void SetBinContent(Int_t bin, Double_t content)
Set bin content.
Definition: TH2.cxx:2441
TLegend
This class displays a legend box (TPaveText) containing several legend entries.
Definition: TLegend.h:23
TLegend::AddEntry
TLegendEntry * AddEntry(const TObject *obj, const char *label="", Option_t *option="lpf")
Add a new entry to this legend.
Definition: TLegend.cxx:330
TLegend::Draw
virtual void Draw(Option_t *option="")
Draw this legend with its current attributes.
Definition: TLegend.cxx:423
TLine
A simple line.
Definition: TLine.h:23
TMatrixDSymEigen
TMatrixDSymEigen.
Definition: TMatrixDSymEigen.h:28
TMatrixTBase::GetNrows
Int_t GetNrows() const
Definition: TMatrixTBase.h:124
TNamed::SetTitle
virtual void SetTitle(const char *title="")
Set the title of the TNamed.
Definition: TNamed.cxx:164
TNamed::GetName
virtual const char * GetName() const
Returns name of object.
Definition: TNamed.h:47
TObject
Mother of all ROOT objects.
Definition: TObject.h:37
TObject::Write
virtual Int_t Write(const char *name=0, Int_t option=0, Int_t bufsize=0)
Write this object to the current directory.
Definition: TObject.cxx:785
TObject::DrawClone
virtual TObject * DrawClone(Option_t *option="") const
Draw a clone of this object in the current selected pad for instance with: gROOT->SetSelectedPad(gPad...
Definition: TObject.cxx:219
TObject::Draw
virtual void Draw(Option_t *option="")
Default Draw method for all objects.
Definition: TObject.cxx:195
TPad
The most important graphics class in the ROOT system.
Definition: TPad.h:29
TPad::Divide
virtual void Divide(Int_t nx=1, Int_t ny=1, Float_t xmargin=0.01, Float_t ymargin=0.01, Int_t color=0)
Automatic pad generation by division.
Definition: TPad.cxx:1163
TPad::SaveAs
virtual void SaveAs(const char *filename="", Option_t *option="") const
Save Pad contents in a file in one of various formats.
Definition: TPad.cxx:5552
TPad::Draw
virtual void Draw(Option_t *option="")
Draw Pad in Current pad (re-parent pad if necessary).
Definition: TPad.cxx:1282
TPad::cd
TVirtualPad * cd(Int_t subpadnumber=0)
Set Current pad.
Definition: TPad.cxx:591
TPad::SetFillStyle
virtual void SetFillStyle(Style_t fstyle)
Override TAttFill::FillStyle for TPad because we want to handle style=0 as style 4000.
Definition: TPad.cxx:5838
TPave::SetBorderSize
virtual void SetBorderSize(Int_t bordersize=4)
Definition: TPave.h:73
TRandom3
Random number generator class based on M.
Definition: TRandom3.h:27
TRandom::Poisson
virtual Int_t Poisson(Double_t mean)
Generates a random integer N according to a Poisson law.
Definition: TRandom.cxx:391
TSpline
Base class for spline implementation containing the Draw/Paint methods.
Definition: TSpline.h:22
TSpline::Draw
virtual void Draw(Option_t *option="")
Draw this function with its current attributes.
Definition: TSpline.cxx:97
TString
Basic string class.
Definition: TString.h:131
TString::Format
static TString Format(const char *fmt,...)
Static method which formats a string using a printf style format descriptor and return a TString.
Definition: TString.cxx:2311
TStyle::SetOptStat
void SetOptStat(Int_t stat=1)
The type of information printed in the histogram statistics box can be selected via the parameter mod...
Definition: TStyle.cxx:1450
TText
Base class for several text objects.
Definition: TText.h:23
TText::SetNDC
virtual void SetNDC(Bool_t isNDC=kTRUE)
Set NDC mode on if isNDC = kTRUE, off otherwise.
Definition: TText.cxx:812
TUnfoldBinning
Binning schemes for use with the unfolding algorithm TUnfoldDensity.
Definition: TUnfoldBinning.h:53
TUnfoldBinning::CreateHistogram
TH1 * CreateHistogram(const char *histogramName, Bool_t originalAxisBinning=kFALSE, Int_t **binMap=0, const char *histogramTitle=0, const char *axisSteering=0) const
Create a THxx histogram capable to hold the bins of this binning node and its children.
Definition: TUnfoldBinning.cxx:742
TUnfoldBinning::GetBinSize
Double_t GetBinSize(Int_t iBin) const
Get N-dimensional bin size.
Definition: TUnfoldBinning.cxx:1723
TUnfoldBinning::GetEndBin
Int_t GetEndBin(void) const
last+1 bin of this node (includes children)
Definition: TUnfoldBinning.h:141
TUnfoldDensity
An algorithm to unfold distributions from detector to truth level.
Definition: TUnfoldDensity.h:48
TUnfoldDensity::GetRhoIJtotal
TH2 * GetRhoIJtotal(const char *histogramName, const char *histogramTitle=0, const char *distributionName=0, const char *projectionMode=0, Bool_t useAxisBinning=kTRUE)
Retrieve correlation coefficients, including all uncertainties.
Definition: TUnfoldDensity.cxx:1012
TUnfoldDensity::kEScanTauRhoAvg
@ kEScanTauRhoAvg
average global correlation coefficient (from TUnfold::GetRhoI())
Definition: TUnfoldDensity.h:107
TUnfoldDensity::GetProbabilityMatrix
TH2 * GetProbabilityMatrix(const char *histogramName, const char *histogramTitle=0, Bool_t useAxisBinning=kTRUE) const
Get matrix of probabilities in a new histogram.
Definition: TUnfoldDensity.cxx:1153
TUnfoldDensity::GetOutput
TH1 * GetOutput(const char *histogramName, const char *histogramTitle=0, const char *distributionName=0, const char *projectionMode=0, Bool_t useAxisBinning=kTRUE) const
retrieve unfolding result as a new histogram
Definition: TUnfoldDensity.cxx:651
TUnfoldDensity::ScanTau
virtual Int_t ScanTau(Int_t nPoint, Double_t tauMin, Double_t tauMax, TSpline **scanResult, Int_t mode=kEScanTauRhoAvg, const char *distribution=0, const char *projectionMode=0, TGraph **lCurvePlot=0, TSpline **logTauXPlot=0, TSpline **logTauYPlot=0)
Scan a function wrt tau and determine the minimum.
Definition: TUnfoldDensity.cxx:1344
TUnfoldDensity::kDensityModeNone
@ kDensityModeNone
no scale factors, matrix L is similar to unity matrix
Definition: TUnfoldDensity.h:65
TUnfoldSys::SetInput
virtual Int_t SetInput(const TH1 *hist_y, Double_t scaleBias=0.0, Double_t oneOverZeroError=0.0, const TH2 *hist_vyy=0, const TH2 *hist_vyy_inv=0)
Define the input data for subsequent calls to DoUnfold(Double_t).
Definition: TUnfoldSys.cxx:444
TUnfoldSys::SubtractBackground
void SubtractBackground(const TH1 *hist_bgr, const char *name, Double_t scale=1.0, Double_t scale_error=0.0)
Specify a source of background.
Definition: TUnfoldSys.cxx:483
TUnfold::DoUnfold
virtual Double_t DoUnfold(void)
Core unfolding algorithm.
Definition: TUnfold.cxx:290
TUnfold::ScanLcurve
virtual Int_t ScanLcurve(Int_t nPoint, Double_t tauMin, Double_t tauMax, TGraph **lCurve, TSpline **logTauX=0, TSpline **logTauY=0, TSpline **logTauCurvature=0)
Scan the L curve, determine tau and unfold at the final value of tau.
Definition: TUnfold.cxx:2548
TUnfold::kEConstraintArea
@ kEConstraintArea
enforce preservation of the area
Definition: TUnfold.h:116
TUnfold::kEConstraintNone
@ kEConstraintNone
use no extra constraint
Definition: TUnfold.h:113
TUnfold::ERegMode
ERegMode
choice of regularisation scheme
Definition: TUnfold.h:120
TUnfold::kRegModeSize
@ kRegModeSize
regularise the amplitude of the output distribution
Definition: TUnfold.h:126
TUnfold::kHistMapOutputHoriz
@ kHistMapOutputHoriz
truth level on x-axis of the response matrix
Definition: TUnfold.h:143
TUnfold::GetTau
Double_t GetTau(void) const
Return regularisation parameter.
Definition: TUnfold.cxx:3185
TVectorT::GetNrows
Int_t GetNrows() const
Definition: TVectorT.h:75
TVirtualFitter::SetFCN
virtual void SetFCN(void(*fcn)(Int_t &, Double_t *, Double_t &f, Double_t *, Int_t))
To set the address of the minimization objective function called by the native compiler (see function...
Definition: TVirtualFitter.cxx:267
TVirtualFitter::Fitter
static TVirtualFitter * Fitter(TObject *obj, Int_t maxpar=25)
Static function returning a pointer to the current fitter.
Definition: TVirtualFitter.cxx:159
text
TText * text
Definition: entrylist_figure1.C:10
line
TLine * line
Definition: entrylistblock_figure1.C:235
sigma
const Double_t sigma
Definition: h1analysisProxy.h:11
c1
return c1
Definition: legend1.C:41
y
Double_t y[n]
Definition: legend1.C:17
x
Double_t x[n]
Definition: legend1.C:17
n
const Int_t n
Definition: legend1.C:16
Cppyy::GetName
std::string GetName(const std::string &scope_name)
Definition: Cppyy.cxx:150
ROOT::Math::Cephes::A
static double A[]
Definition: SpecFuncCephes.cxx:170
TGeant4Unit::s
static constexpr double s
Definition: TGeant4SystemOfUnits.h:162
TGeant4Unit::second
static constexpr double second
Definition: TGeant4SystemOfUnits.h:151
TMath::Max
Short_t Max(Short_t a, Short_t b)
Definition: TMathBase.h:212
TMath::Prob
Double_t Prob(Double_t chi2, Int_t ndf)
Computation of the probability for a certain Chi-squared (chi2) and number of degrees of freedom (ndf...
Definition: TMath.cxx:621
TMath::Sqrt
Double_t Sqrt(Double_t x)
Definition: TMath.h:681
TMath::Power
LongDouble_t Power(LongDouble_t x, LongDouble_t y)
Definition: TMath.h:725
TMath::Min
Short_t Min(Short_t a, Short_t b)
Definition: TMathBase.h:180
TMath::Hypot
Double_t Hypot(Double_t x, Double_t y)
Definition: TMath.cxx:57
TMath::LandauI
Double_t LandauI(Double_t x)
Returns the value of the Landau distribution function at point x.
Definition: TMath.cxx:2803
TMath::Abs
Short_t Abs(Short_t d)
Definition: TMathBase.h:120
first
Definition: first.py:1
graph
Definition: graph.py:1
test
Definition: test.py:1
v
@ v
Definition: rootcling_impl.cxx:3622
v1
@ v1
Definition: rootcling_impl.cxx:3624
style
TCanvas * style()
Definition: style.C:1
Draw
th1 Draw()
sum
static long int sum(long int i)
Definition: Factory.cxx:2276

Version 17.6, in parallel to changes in TUnfold

This file is part of TUnfold.

TUnfold is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

TUnfold is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with TUnfold. If not, see http://www.gnu.org/licenses/.

Author
Stefan Schmitt DESY, 14.10.2008

Definition in file testUnfold7c.C.