␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m
Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
All rights reserved, please read http://roofit.sourceforge.net/license.txt
[#1] INFO:NumericIntegration -- RooRealIntegral::init([gaussy_NORM[y]_X_gaussx_NORM[x]]_Int[y]) using numeric integrator RooIntegrator1D to calculate Int(y)
[#1] INFO:NumericIntegration -- RooRealIntegral::init([gaussy_NORM[y]_X_gaussx_NORM[x]]_Int[y]) using numeric integrator RooIntegrator1D to calculate Int(y)
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
[#1] INFO:Minization -- The following expressions will be evaluated in cache-and-track mode: (gaussx)
[#0] WARNING:Minization -- RooMinimizerFcn::synchronize: WARNING: no initial error estimate available for a1: using 0.4
**********
** 1 **SET PRINT 1
**********
**********
** 2 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 a1 -1.50000e+00 4.00000e-01 -3.00000e+00 1.00000e+00
**********
** 3 **SET ERR 0.5
**********
**********
** 4 **SET PRINT 1
**********
**********
** 5 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 6 **MIGRAD 500 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
prevFCN = 1900.156536 START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
a1=-1.491,
prevFCN = 1900.000822 a1=-1.509,
prevFCN = 1900.423606 a1=-1.499,
prevFCN = 1900.135899 a1=-1.501,
prevFCN = 1900.178287 FCN=1900.16 FROM MIGRAD STATUS=INITIATE 4 CALLS 5 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a1 -1.50000e+00 4.00000e-01 2.08372e-01 -4.77802e+01
ERR DEF= 0.5
a1=-1.484,
prevFCN = 1899.958651 a1=-1.483,
prevFCN = 1899.959675 a1=-1.484,
prevFCN = 1899.958586 a1=-1.484,
prevFCN = 1899.958497 a1=-1.483,
prevFCN = 1899.958935 a1=-1.485,
prevFCN = 1899.958964 MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
a1=-1.484,
prevFCN = 1899.958497 a1=-1.483,
prevFCN = 1899.958935 a1=-1.485,
prevFCN = 1899.958964 a1=-1.484,
prevFCN = 1899.958512 a1=-1.484,
prevFCN = 1899.958518 COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=1899.96 FROM MIGRAD STATUS=CONVERGED 15 CALLS 16 TOTAL
EDM=2.41873e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a1 -1.48409e+00 2.51054e-02 3.89173e-04 -3.80132e-02
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 1 ERR DEF=0.5
6.303e-04
a1=-1.484, **********
** 7 **SET ERR 0.5
**********
**********
** 8 **SET PRINT 1
**********
**********
** 9 **HESSE 500
**********
prevFCN = 1899.958497 a1=-1.484,
prevFCN = 1899.958512 a1=-1.484,
prevFCN = 1899.958518 a1=-1.484,
prevFCN = 1899.958497 a1=-1.484,
prevFCN = 1899.958498 COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=1899.96 FROM HESSE STATUS=OK 5 CALLS 21 TOTAL
EDM=2.42353e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 a1 -1.48409e+00 2.51054e-02 7.78346e-05 -2.44471e-01
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 1 ERR DEF=0.5
6.303e-04
a1=-1.484, [#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init([gaussy_NORM[y]_X_gaussx_NORM[x]]_Int[y]) using numeric integrator RooIntegrator1D to calculate Int(y)
{
RooRealVar sigmax(
"sigmax",
"width of gaussian", 0.5);
RooGaussian gaussx(
"gaussx",
"Gaussian in x with shifting mean in y",
x, fy, sigmax);
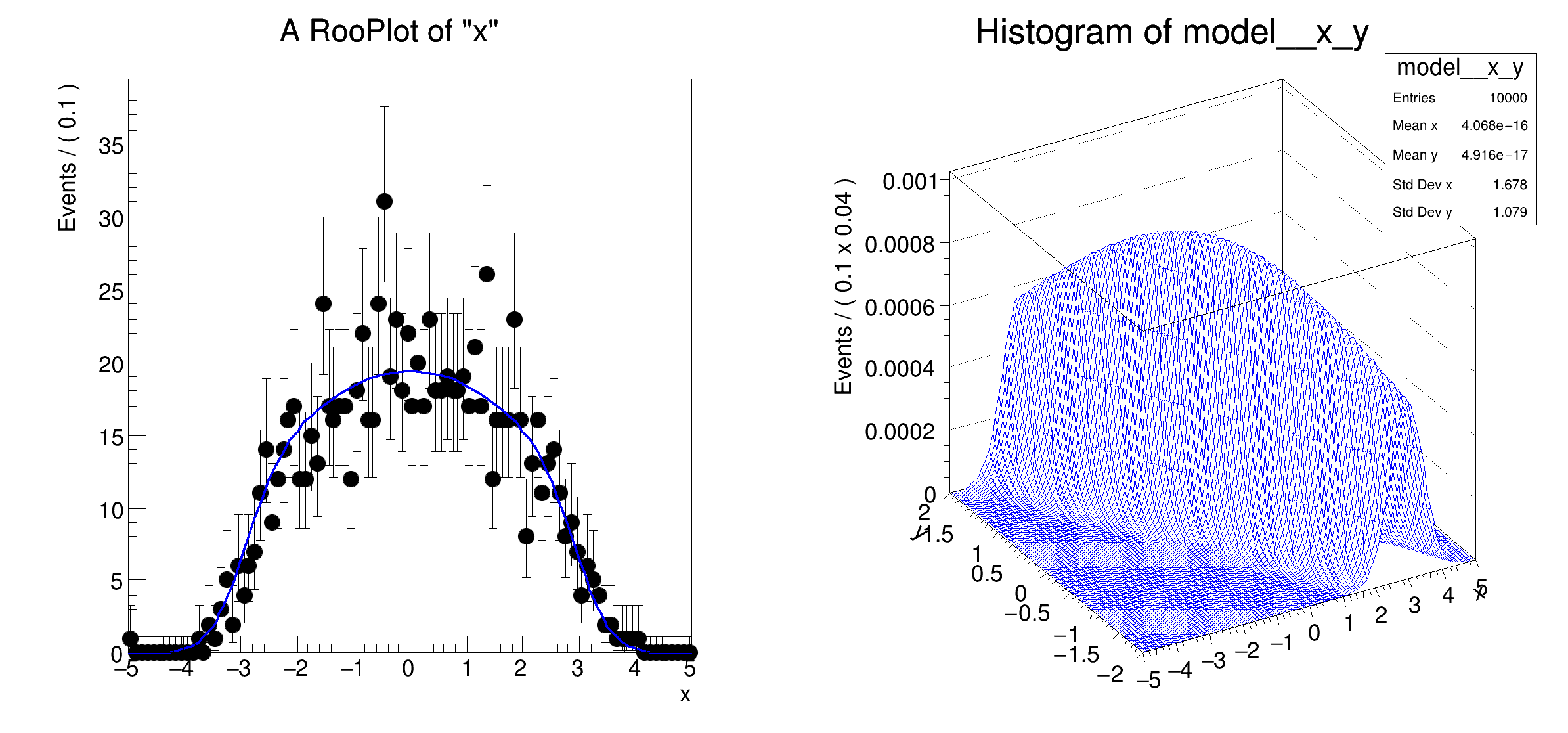
TH1 *hh = model.createHistogram(
"x,y");
TCanvas *
c =
new TCanvas(
"rf315_projectpdf",
"rf315_projectpdf", 800, 400);
gPad->SetLeftMargin(0.15);
gPad->SetLeftMargin(0.20);
}
RooAbsData is the common abstract base class for binned and unbinned datasets.
virtual RooPlot * plotOn(RooPlot *frame, const RooCmdArg &arg1=RooCmdArg::none(), const RooCmdArg &arg2=RooCmdArg::none(), const RooCmdArg &arg3=RooCmdArg::none(), const RooCmdArg &arg4=RooCmdArg::none(), const RooCmdArg &arg5=RooCmdArg::none(), const RooCmdArg &arg6=RooCmdArg::none(), const RooCmdArg &arg7=RooCmdArg::none(), const RooCmdArg &arg8=RooCmdArg::none()) const
Calls RooPlot* plotOn(RooPlot* frame, const RooLinkedList& cmdList) const ;.
virtual RooDataHist * generateBinned(const RooArgSet &whatVars, Double_t nEvents, const RooCmdArg &arg1, const RooCmdArg &arg2=RooCmdArg::none(), const RooCmdArg &arg3=RooCmdArg::none(), const RooCmdArg &arg4=RooCmdArg::none(), const RooCmdArg &arg5=RooCmdArg::none()) const
As RooAbsPdf::generateBinned(const RooArgSet&, const RooCmdArg&,const RooCmdArg&, const RooCmdArg&,...
virtual RooFitResult * fitTo(RooAbsData &data, const RooCmdArg &arg1=RooCmdArg::none(), const RooCmdArg &arg2=RooCmdArg::none(), const RooCmdArg &arg3=RooCmdArg::none(), const RooCmdArg &arg4=RooCmdArg::none(), const RooCmdArg &arg5=RooCmdArg::none(), const RooCmdArg &arg6=RooCmdArg::none(), const RooCmdArg &arg7=RooCmdArg::none(), const RooCmdArg &arg8=RooCmdArg::none())
Fit PDF to given dataset.
virtual RooAbsPdf * createProjection(const RooArgSet &iset)
Return a p.d.f that represent a projection of this p.d.f integrated over given observables.
virtual RooPlot * plotOn(RooPlot *frame, const RooCmdArg &arg1=RooCmdArg::none(), const RooCmdArg &arg2=RooCmdArg::none(), const RooCmdArg &arg3=RooCmdArg::none(), const RooCmdArg &arg4=RooCmdArg::none(), const RooCmdArg &arg5=RooCmdArg::none(), const RooCmdArg &arg6=RooCmdArg::none(), const RooCmdArg &arg7=RooCmdArg::none(), const RooCmdArg &arg8=RooCmdArg::none(), const RooCmdArg &arg9=RooCmdArg::none(), const RooCmdArg &arg10=RooCmdArg::none()) const
Helper calling plotOn(RooPlot*, RooLinkedList&) const.
static RooNumIntConfig * defaultIntegratorConfig()
Returns the default numeric integration configuration for all RooAbsReals.
RooArgSet is a container object that can hold multiple RooAbsArg objects.
void setEpsAbs(Double_t newEpsAbs)
Set absolute convergence criteria (convergence if abs(Err)<newEpsAbs)
void setEpsRel(Double_t newEpsRel)
Set relative convergence criteria (convergence if abs(Err)/abs(Int)<newEpsRel)
A RooPlot is a plot frame and a container for graphics objects within that frame.
virtual void Draw(Option_t *options=0)
Draw this plot and all of the elements it contains.
Class RooPolyVar is a RooAbsReal implementing a polynomial in terms of a list of RooAbsReal coefficie...
RooProdPdf is an efficient implementation of a product of PDFs of the form.
RooRealVar represents a variable that can be changed from the outside.
virtual void SetTitleOffset(Float_t offset=1)
Set distance between the axis and the axis title.
virtual void SetLineColor(Color_t lcolor)
Set the line color.
virtual void Draw(Option_t *option="")
Draw this histogram with options.
The namespace RooFit contains mostly switches that change the behaviour of functions of PDFs (or othe...
RooConstVar & RooConst(Double_t val)
RooCmdArg Verbose(Bool_t flag=kTRUE)
RooCmdArg Conditional(const RooArgSet &pdfSet, const RooArgSet &depSet, Bool_t depsAreCond=kFALSE)

 Multidimensional models: marginizalization of multi-dimensional p.d.f.s through integration
Multidimensional models: marginizalization of multi-dimensional p.d.f.s through integration