goftest.C File Reference

Detailed Description

GoFTest tutorial macro

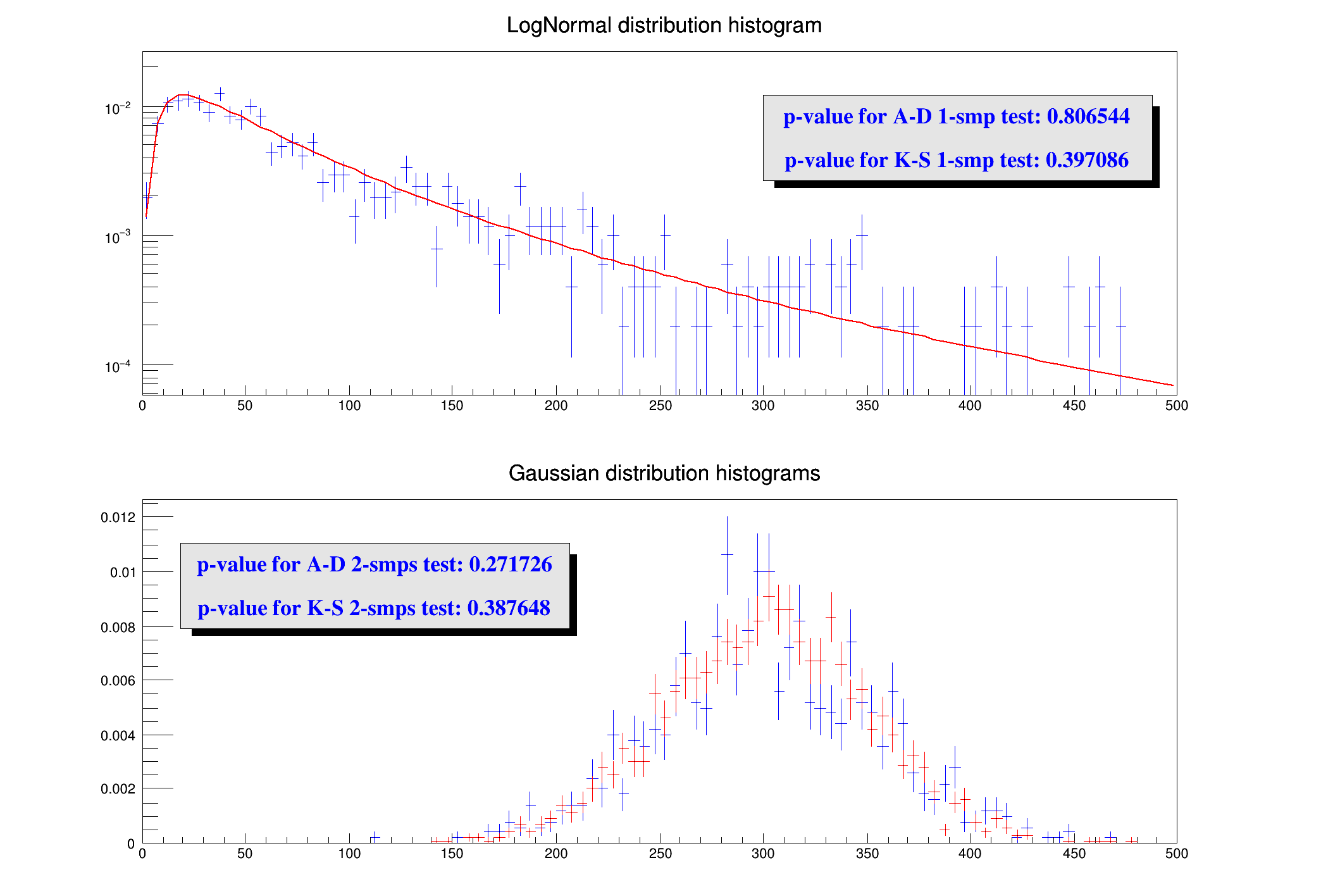
Using Anderson-Darling and Kolmogorov-Smirnov goodness of fit tests 1 sample test is performed comparing data with a log-normal distribution and a 2 sample test is done comparing two gaussian data sets.

 
 
 
TEST with LANDAU distribution:   OK ( pvalues = 0.777278  )

 
#include <cassert>
#include "TCanvas.h"
#include "TPaveText.h"
#include "TH1.h"
#include "TF1.h"
#include "Math/GoFTest.h"
#include "Math/Functor.h"
#include "TRandom3.h"
#include "Math/DistFunc.h"
 
// need to use Functor1D
double landau(double x) {
   return ROOT::Math::landau_pdf(x);
}
 
void goftest() {
 
   // ------------------------------------------------------------------------
   // Case 1: Create logNormal random sample
   
 
   UInt_t nEvents1 = 1000;
 
   //ROOT::Math::Random<ROOT::Math::GSLRngMT> r;
   TF1 * f1 = new TF1("logNormal","ROOT::Math::lognormal_pdf(x,[0],[1])",0,500);
   // set the lognormal parameters (m and s)
   f1->SetParameters(4.0,1.0);
   f1->SetNpx(1000);
 
 
   Double_t* sample1 = new Double_t[nEvents1];
 
   TH1D* h1smp = new TH1D("h1smp", "LogNormal distribution histogram", 100, 0, 500);
   h1smp->SetStats(kFALSE);
 
   for (UInt_t i = 0; i < nEvents1; ++i) {
      //Double_t data = f1->GetRandom();
      Double_t data = gRandom->Gaus(4,1);
      data = TMath::Exp(data);
      sample1[i] = data;
      h1smp->Fill(data);
   }
   // normalize correctly the histogram using the entries inside
   h1smp->Scale( ROOT::Math::lognormal_cdf(500.,4.,1) / nEvents1, "width");
 
   TCanvas* c = new TCanvas("c","1-Sample and 2-Samples GoF Tests");
   c->Divide(1, 2);
   TPad * pad = (TPad *)c->cd(1);
   h1smp->Draw();
   h1smp->SetLineColor(kBlue);
   pad->SetLogy();
   f1->SetNpx(100); // use same points as histo for drawing
   f1->SetLineColor(kRed);
   f1->Draw("SAME");
 
   // -----------------------------------------
   // Create GoFTest object
   
 
   ROOT::Math::GoFTest* goftest_1 = new ROOT::Math::GoFTest(nEvents1, sample1, ROOT::Math::GoFTest::kLogNormal);
   //----------------------------------------------------
   // Possible calls for the Anderson - DarlingTest test 
   // a) Returning the Anderson-Darling standardized test statistic 
   Double_t A2_1 = goftest_1-> AndersonDarlingTest("t");
   Double_t A2_2 = (*goftest_1)(ROOT::Math::GoFTest::kAD, "t");
   assert(A2_1 == A2_2);
 
   // b) Returning the p-value for the Anderson-Darling test statistic 
   Double_t pvalueAD_1 = goftest_1-> AndersonDarlingTest(); // p-value is the default choice
   Double_t pvalueAD_2 = (*goftest_1)(); // p-value and Anderson - Darling Test are the default choices
   assert(pvalueAD_1 == pvalueAD_2);
 
   // Rebuild the test using the default 1-sample construtor 
   delete goftest_1;
   goftest_1 = new ROOT::Math::GoFTest(nEvents1, sample1 ); // User must then input a distribution type option
   goftest_1->SetDistribution(ROOT::Math::GoFTest::kLogNormal);
 
   //--------------------------------------------------
   // Possible calls for the Kolmogorov - Smirnov test 
   // a) Returning the Kolmogorov-Smirnov standardized test statistic 
   Double_t Dn_1 = goftest_1-> KolmogorovSmirnovTest("t");
   Double_t Dn_2 = (*goftest_1)(ROOT::Math::GoFTest::kKS, "t");
   assert(Dn_1 == Dn_2);
 
   // b) Returning the p-value for the Kolmogorov-Smirnov test statistic 
   Double_t pvalueKS_1 = goftest_1-> KolmogorovSmirnovTest();
   Double_t pvalueKS_2 = (*goftest_1)(ROOT::Math::GoFTest::kKS);
   assert(pvalueKS_1 == pvalueKS_2);
 
   // Valid but incorrect calls for the 2-samples methods of the 1-samples constructed goftest_1
#ifdef TEST_ERROR_MESSAGE
    Double_t A2 = (*goftest_1)(ROOT::Math::GoFTest::kAD2s, "t");     // Issues error message
    Double_t pvalueKS = (*goftest_1)(ROOT::Math::GoFTest::kKS2s);    // Issues error message
    assert(A2 == pvalueKS);
#endif
 
   TPaveText* pt1 = new TPaveText(0.58, 0.6, 0.88, 0.80, "brNDC");
   Char_t str1[50];
   sprintf(str1, "p-value for A-D 1-smp test: %f", pvalueAD_1);
   pt1->AddText(str1);
   pt1->SetFillColor(18);
   pt1->SetTextFont(20);
   pt1->SetTextColor(4);
   Char_t str2[50];
   sprintf(str2, "p-value for K-S 1-smp test: %f", pvalueKS_1);
   pt1->AddText(str2);
   pt1->Draw();
 
   // ------------------------------------------------------------------------
   // Case 2: Create Gaussian random samples
  
   UInt_t nEvents2 = 2000;
 
   Double_t* sample2 = new Double_t[nEvents2];
 
   TH1D* h2smps_1 = new TH1D("h2smps_1", "Gaussian distribution histograms", 100, 0, 500);
   h2smps_1->SetStats(kFALSE);
 
   TH1D* h2smps_2 = new TH1D("h2smps_2", "Gaussian distribution histograms", 100, 0, 500);
   h2smps_2->SetStats(kFALSE);
 
   TRandom3 r;
   for (UInt_t i = 0; i < nEvents1; ++i) {
      Double_t data = r.Gaus(300, 50);
      sample1[i] = data;
      h2smps_1->Fill(data);
   }
   h2smps_1->Scale(1. / nEvents1, "width");
   c->cd(2);
   h2smps_1->Draw();
   h2smps_1->SetLineColor(kBlue);
 
   for (UInt_t i = 0; i < nEvents2; ++i) {
      Double_t data = r.Gaus(300, 50);
      sample2[i] = data;
      h2smps_2->Fill(data);
   }
   h2smps_2->Scale(1. / nEvents2, "width");
   h2smps_2->Draw("SAME");
   h2smps_2->SetLineColor(kRed);
 
   // -----------------------------------------
   // Create GoFTest object
   
   ROOT::Math::GoFTest* goftest_2 = new ROOT::Math::GoFTest(nEvents1, sample1, nEvents2, sample2);
 
      //----------------------------------------------------
   // Possible calls for the Anderson - DarlingTest test 
   // a) Returning the Anderson-Darling standardized test statistic
   A2_1 = goftest_2->AndersonDarling2SamplesTest("t");
   A2_2 = (*goftest_2)(ROOT::Math::GoFTest::kAD2s, "t");
   assert(A2_1 == A2_2);
 
   // b) Returning the p-value for the Anderson-Darling test statistic 
   pvalueAD_1 = goftest_2-> AndersonDarling2SamplesTest(); // p-value is the default choice
   pvalueAD_2 = (*goftest_2)(ROOT::Math::GoFTest::kAD2s);  // p-value is the default choices
   assert(pvalueAD_1 == pvalueAD_2);
 
   //--------------------------------------------------
   // Possible calls for the Kolmogorov - Smirnov test 
   // a) Returning the Kolmogorov-Smirnov standardized test statistic 
   Dn_1 = goftest_2-> KolmogorovSmirnov2SamplesTest("t");
   Dn_2 = (*goftest_2)(ROOT::Math::GoFTest::kKS2s, "t");
   assert(Dn_1 == Dn_2);
 
   // b) Returning the p-value for the Kolmogorov-Smirnov test statistic 
   pvalueKS_1 = goftest_2-> KolmogorovSmirnov2SamplesTest();
   pvalueKS_2 = (*goftest_2)(ROOT::Math::GoFTest::kKS2s);
   assert(pvalueKS_1 == pvalueKS_2);
 
#ifdef TEST_ERROR_MESSAGE
   /* Valid but incorrect calls for the 1-sample methods of the 2-samples constucted goftest_2 */
   A2 = (*goftest_2)(ROOT::Math::GoFTest::kAD, "t");     // Issues error message
   pvalueKS = (*goftest_2)(ROOT::Math::GoFTest::kKS);    // Issues error message
   assert(A2 == pvalueKS);
#endif
 
   TPaveText* pt2 = new TPaveText(0.13, 0.6, 0.43, 0.8, "brNDC");
   sprintf(str1, "p-value for A-D 2-smps test: %f", pvalueAD_1);
   pt2->AddText(str1);
   pt2->SetFillColor(18);
   pt2->SetTextFont(20);
   pt2->SetTextColor(4);
   sprintf(str2, "p-value for K-S 2-smps test: %f", pvalueKS_1);
   pt2-> AddText(str2);
   pt2-> Draw();
 
   // ------------------------------------------------------------------------
   // Case 3: Create Landau random sample
 
   UInt_t nEvents3 = 1000;
 
   Double_t* sample3 = new Double_t[nEvents3];
   for (UInt_t i = 0; i < nEvents3; ++i) {
      Double_t data = r.Landau();
      sample3[i] = data;
   }
 
   // ------------------------------------------
   // Create GoFTest objects
   //
   // Possible constructors for the user input distribution 
 
   // a) User input PDF 
   ROOT::Math::Functor1D f(&landau);
   double minimum = 3*TMath::MinElement(nEvents3, sample3);
   double maximum = 3*TMath::MaxElement(nEvents3, sample3);
   ROOT::Math::GoFTest* goftest_3a = new ROOT::Math::GoFTest(nEvents3, sample3, f,  ROOT::Math::GoFTest::kPDF, minimum,maximum);  // need to specify am interval
   // b) User input CDF 
   ROOT::Math::Functor1D fI(&TMath::LandauI);
   ROOT::Math::GoFTest* goftest_3b = new ROOT::Math::GoFTest(nEvents3, sample3, fI, ROOT::Math::GoFTest::kCDF,minimum,maximum);
 
 
   // Returning the p-value for the Anderson-Darling test statistic 
   pvalueAD_1 = goftest_3a-> AndersonDarlingTest(); // p-value is the default choice
 
   pvalueAD_2 = (*goftest_3b)(); // p-value and Anderson - Darling Test are the default choices
 
   // Checking consistency between both tests 
   std::cout << " \n\nTEST with LANDAU distribution:\t";
   if (TMath::Abs(pvalueAD_1 - pvalueAD_2) > 1.E-1 * pvalueAD_2) {
      std::cout << "FAILED " << std::endl;
      Error("goftest","Error in comparing testing using Landau and Landau CDF");
      std::cerr << " pvalues are " << pvalueAD_1 << "  " << pvalueAD_2 << std::endl;
   }
   else
      std::cout << "OK ( pvalues = " << pvalueAD_2 << "  )" << std::endl;
}

Author

Bartolomeu Rabacal

Definition in file goftest.C.