float16.C File Reference

Detailed Description

Tutorial illustrating use and precision of the Float16_t data type.

See the double32.C tutorial for all the details.

 
#include "ROOT/TSeq.hxx"
#include "TCanvas.h"
#include "TFile.h"
#include "TGraph.h"
#include "TH1.h"
#include "TLegend.h"
#include "TMath.h"
#include "TRandom3.h"
#include "TTree.h"
 
class DemoFloat16 {
private:
   float fF32;     // reference member with full single precision
   Float16_t fF16; // saved as a 16 bit floating point number
   Float16_t fI16; //[-pi,pi]    saved as a 16 bit unsigned int
   Float16_t fI14; //[-pi,pi,14] saved as a 14 bit unsigned int
   Float16_t fI10; //[-pi,pi,10] saved as a 10 bit unsigned int
   Float16_t fI8;  //[-pi,pi,8] saved as a 8 bit unsigned int
   Float16_t fI6;  //[-pi,pi,6] saved as a 6 bit unsigned int
   Float16_t fI4;  //[-pi,pi,4] saved as a 4 bit unsigned int
   Float16_t fR8;  //[0, 0, 8] saved as a 16 bit float with a 8 bits mantissa
   Float16_t fR6;  //[0, 0, 6] saved as a 16 bit float with a 6 bits mantissa
   Float16_t fR4;  //[0, 0, 4] saved as a 16 bit float with a 4 bits mantissa
   Float16_t fR2;  //[0, 0, 2] saved as a 16 bit float with a 2 bits mantissa
 
public:
   DemoFloat16() = default;
   void Set(float ref) { fF32 = fF16 = fI16 = fI14 = fI10 = fI8 = fI6 = fI4 = fR8 = fR6 = fR4 = fR2 = ref; }
};
 
void float16()
{
   const auto nEntries = 200000;
   const auto xmax = TMath::Pi();
   const auto xmin = -xmax;
 
   // create a Tree with nEntries objects DemoFloat16
   TFile::Open("DemoFloat16.root", "recreate");
   TTree tree("tree", "DemoFloat16");
   DemoFloat16 demoInstance;
   auto demoInstanceBranch = tree.Branch("d", "DemoFloat16", &demoInstance, 4000);
   TRandom3 r;
   for (auto i : ROOT::TSeqI(nEntries)) {
      demoInstance.Set(r.Uniform(xmin, xmax));
      tree.Fill();
   }
   tree.Write();
 
   // Now we can proceed with the analysis of the sizes on disk of all branches
 
   // Create the frame histogram and the graphs
   auto branches = demoInstanceBranch->GetListOfBranches();
   const auto nb = branches->GetEntries();
   auto br = static_cast<TBranch *>(branches->At(0));
   const Long64_t zip64 = br->GetZipBytes();
 
   auto h = new TH1F("h", "Float16_t compression and precision", nb, 0, nb);
   h->SetMaximum(18);
   h->SetStats(0);
 
   auto gcx = new TGraph();
   gcx->SetName("gcx");
   gcx->SetMarkerStyle(kFullSquare);
   gcx->SetMarkerColor(kBlue);
 
   auto gdrange = new TGraph();
   gdrange->SetName("gdrange");
   gdrange->SetMarkerStyle(kFullCircle);
   gdrange->SetMarkerColor(kRed);
 
   auto gdval = new TGraph();
   gdval->SetName("gdval");
   gdval->SetMarkerStyle(kFullTriangleUp);
   gdval->SetMarkerColor(kBlack);
 
   // loop on branches to get the precision and compression factors
   for (auto i : ROOT::TSeqI(nb)) {
      br = static_cast<TBranch *>(branches->At(i));
      const auto brName = br->GetName();
      h->GetXaxis()->SetBinLabel(i + 1, brName);
      auto const cx = double(zip64) / br->GetZipBytes();
      gcx->SetPoint(i, i + 0.5, cx);
      if (i == 0) continue;
 
      tree.Draw(Form("(fF32-%s)/(%g)", brName, xmax - xmin), "", "goff");
      const auto rmsDrange = TMath::RMS(nEntries, tree.GetV1());
      const auto drange = TMath::Max(0., -TMath::Log10(rmsDrange));
      gdrange->SetPoint(i - 1, i + 0.5, drange);
 
      tree.Draw(Form("(fF32-%s)/fF32 >> hdval_%s", brName, brName), "", "goff");
      const auto rmsDval = TMath::RMS(nEntries, tree.GetV1());
      const auto dval = TMath::Max(0., -TMath::Log10(rmsDval));
      gdval->SetPoint(i - 1, i + 0.5, dval);
 
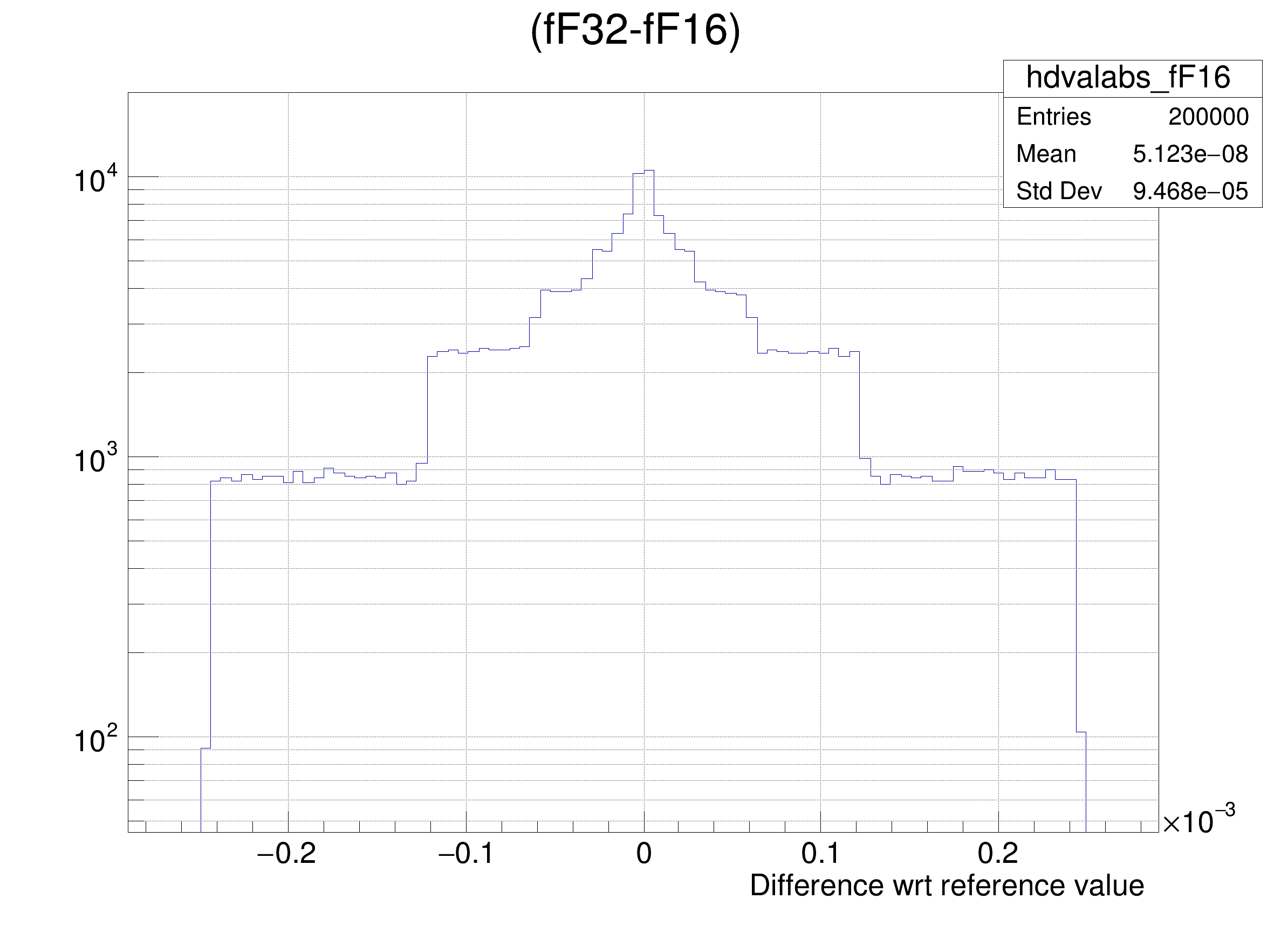
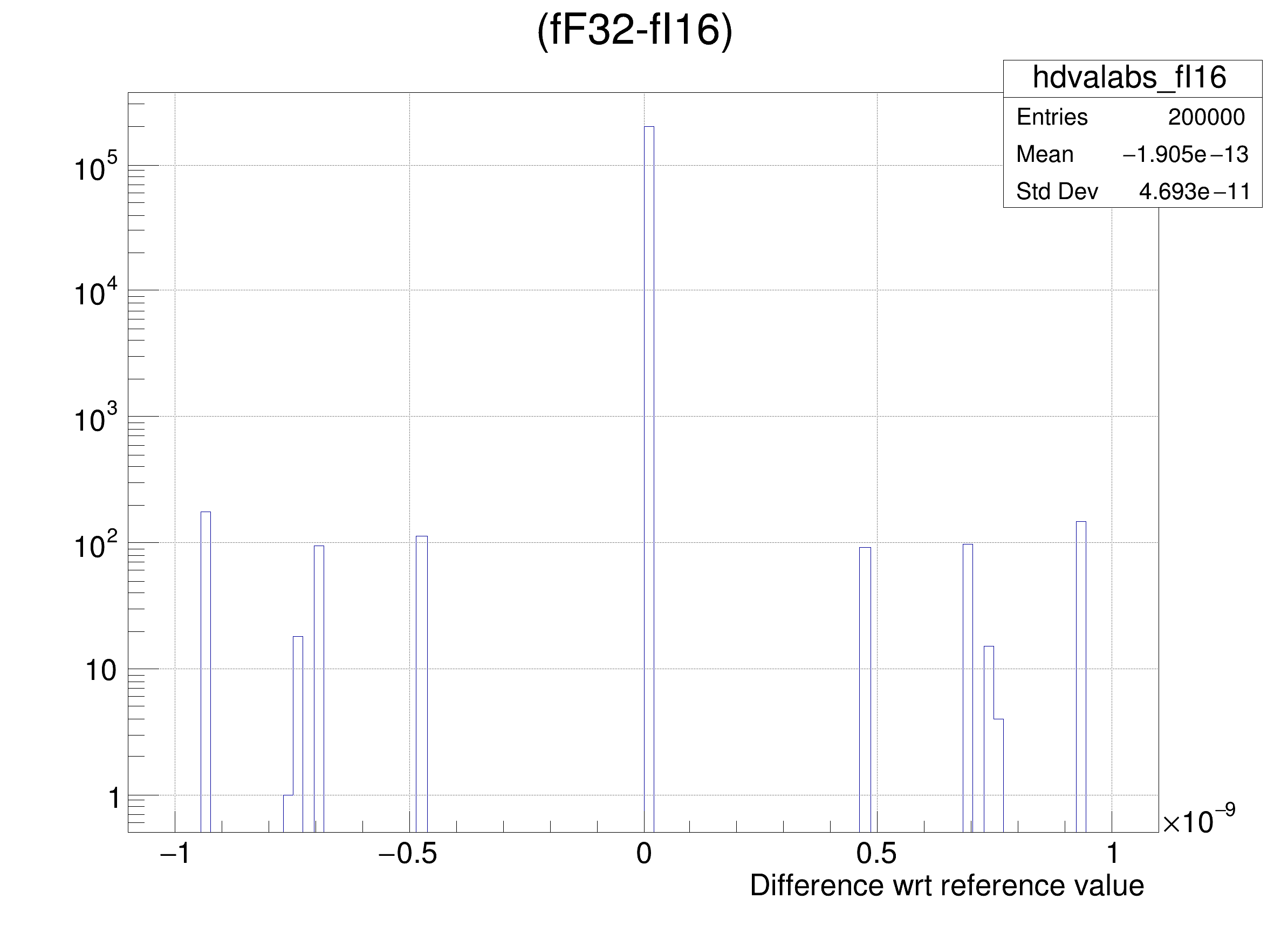
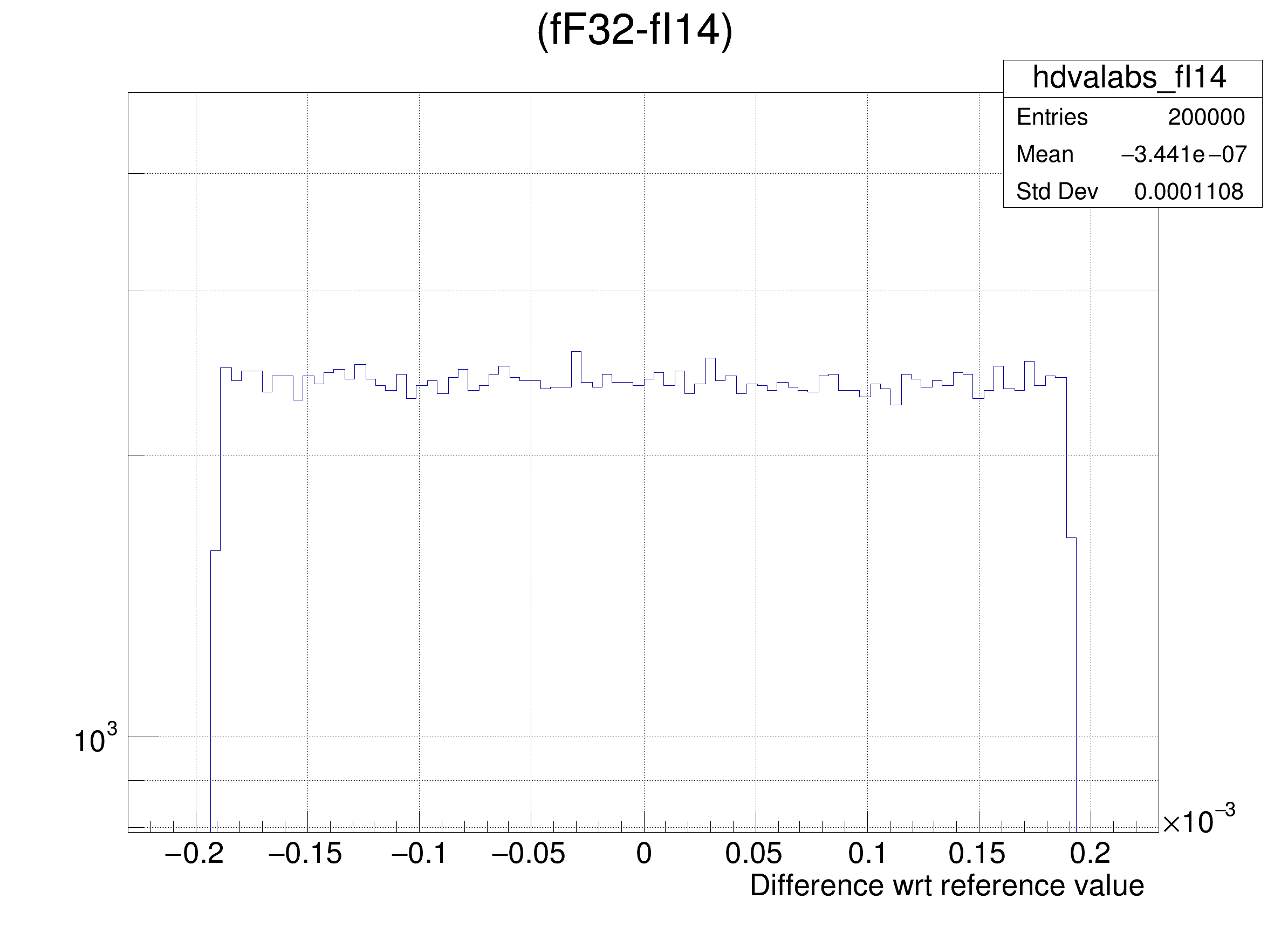
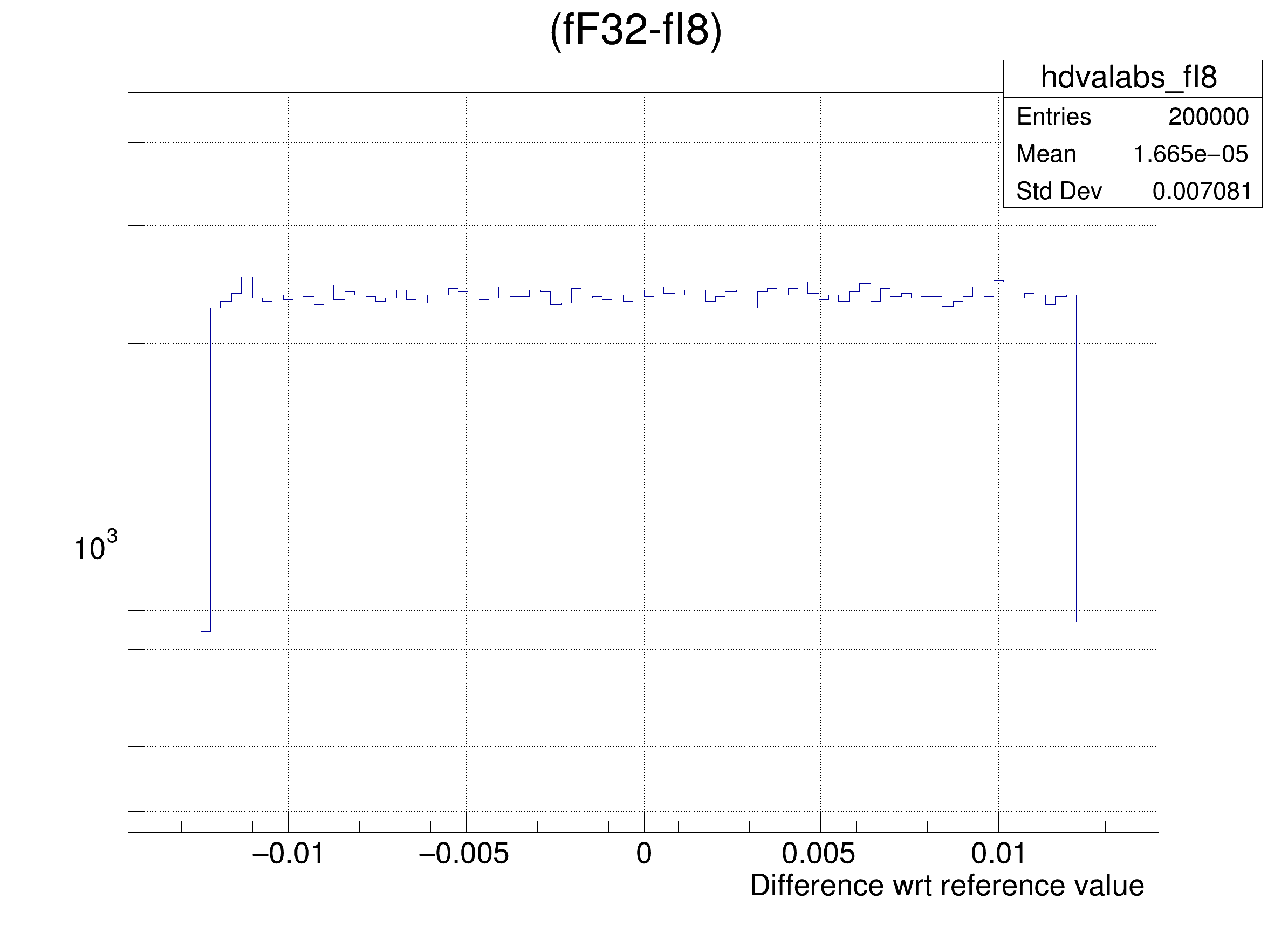
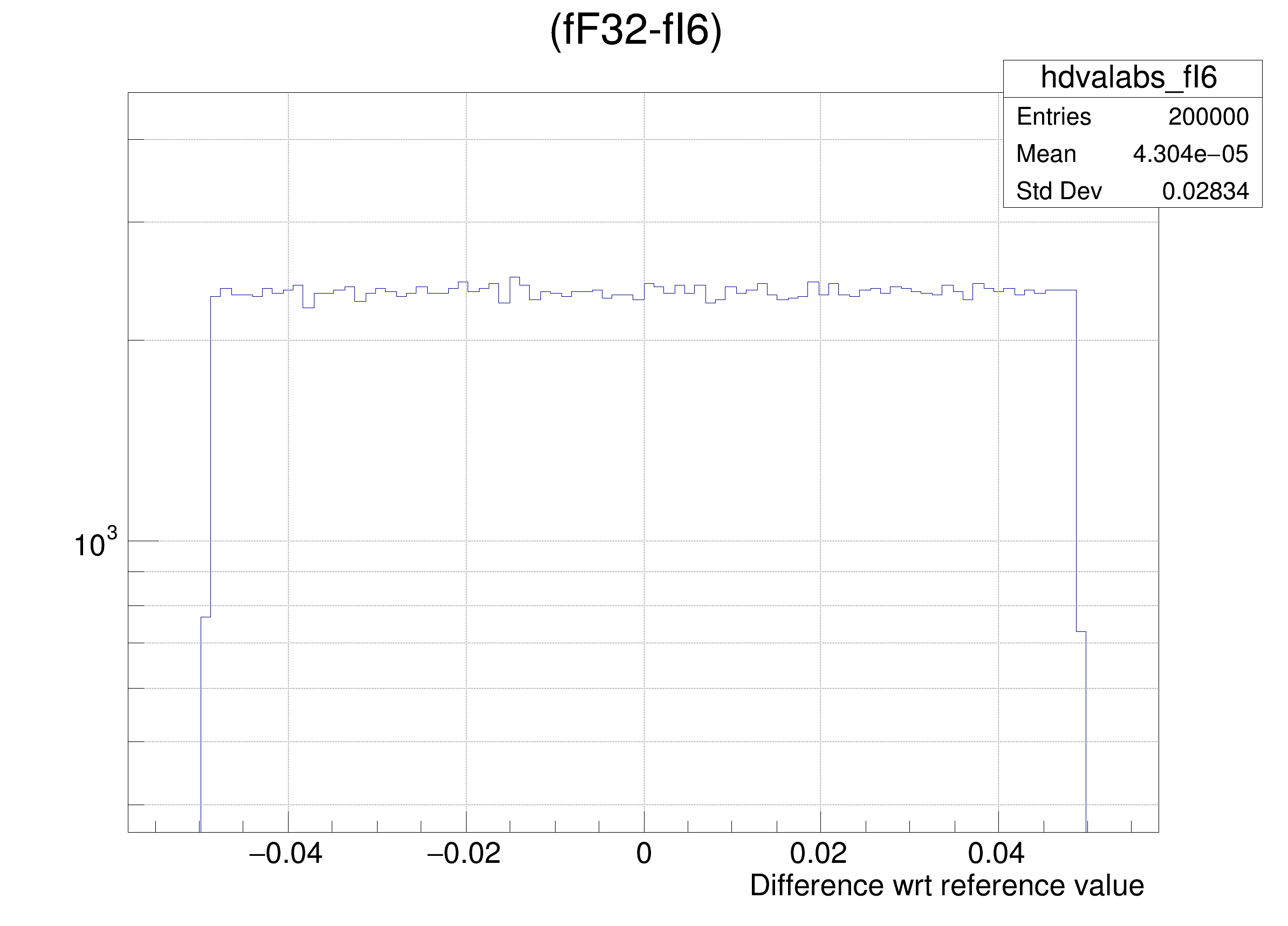
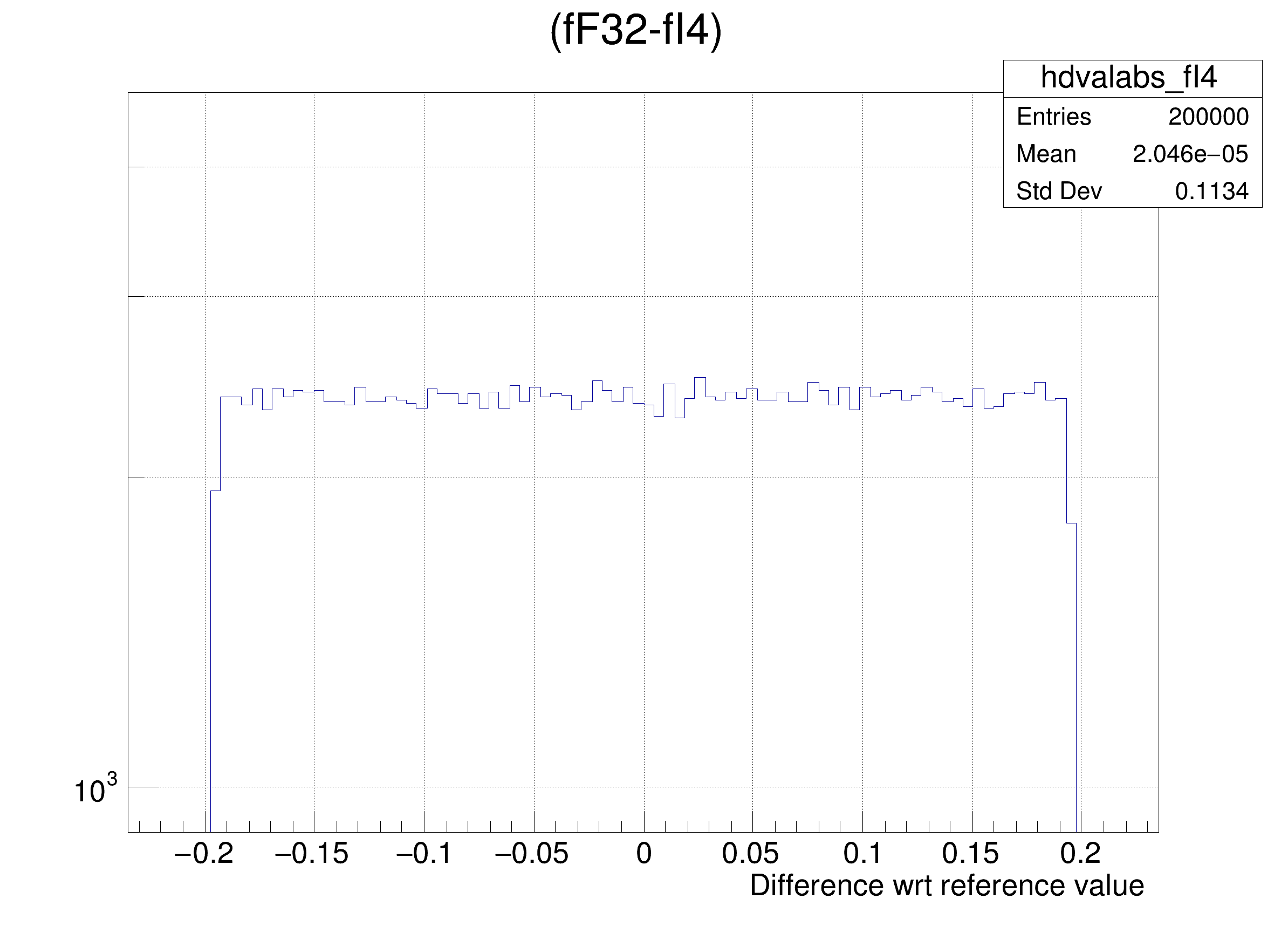
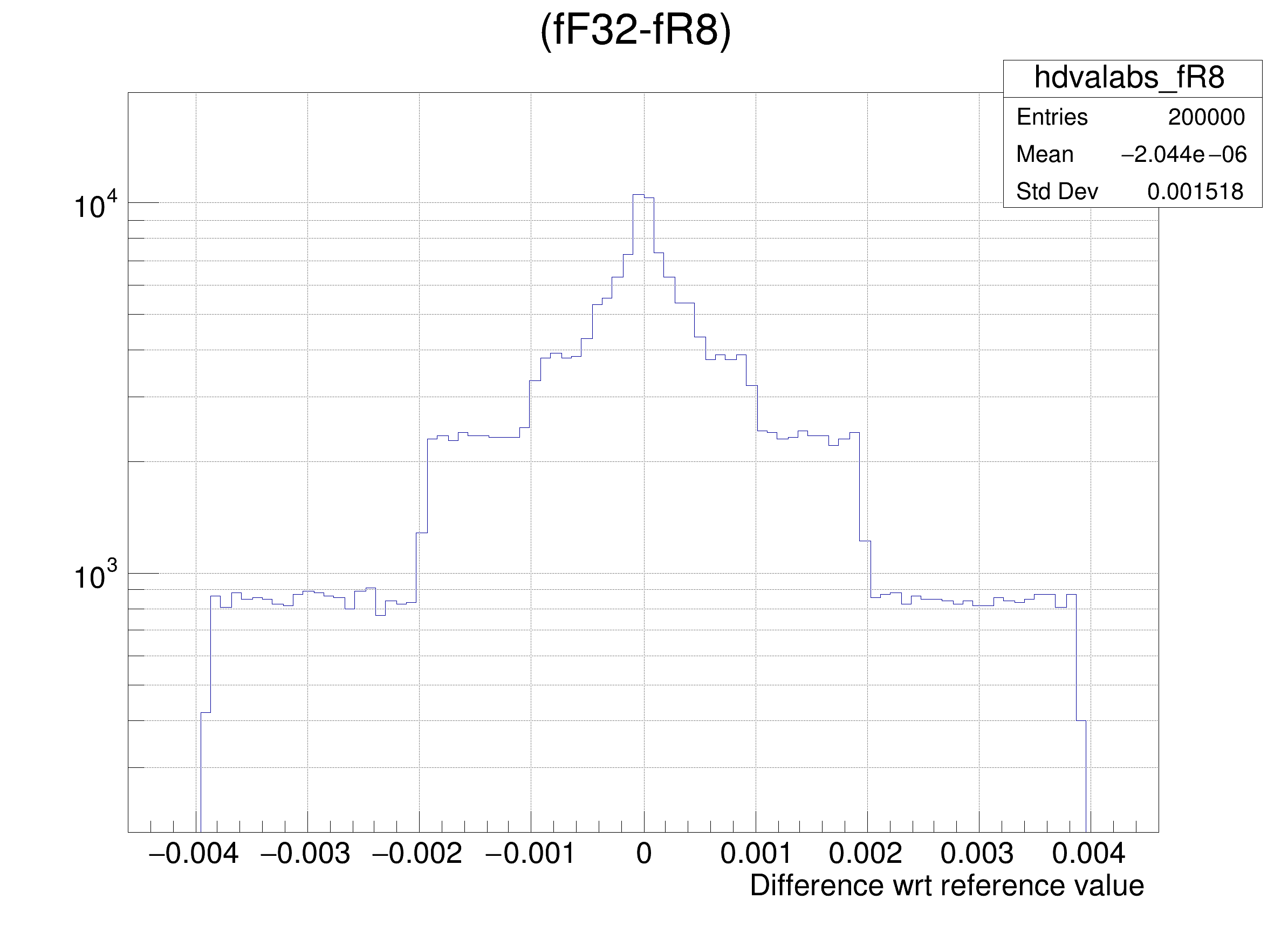
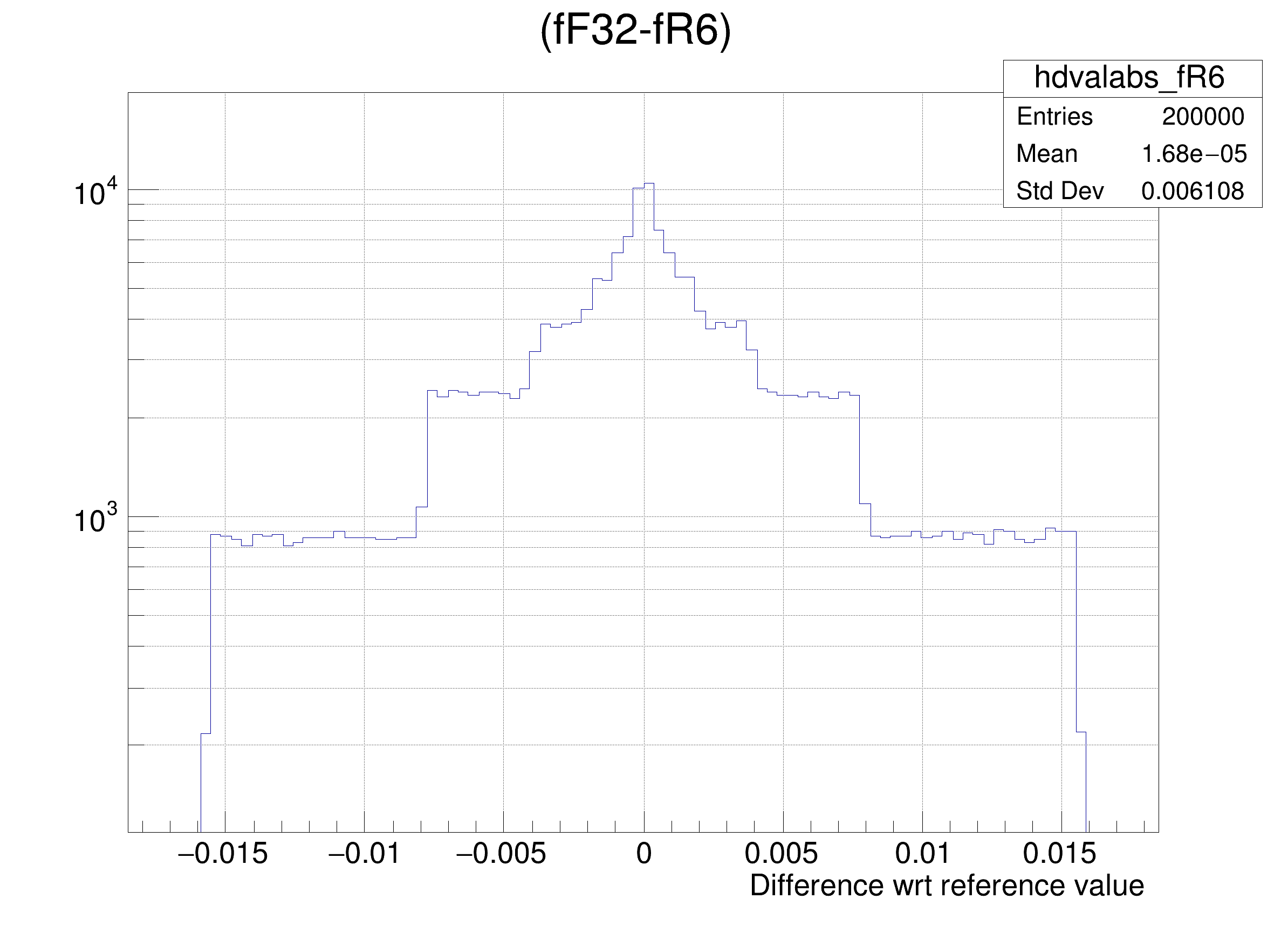
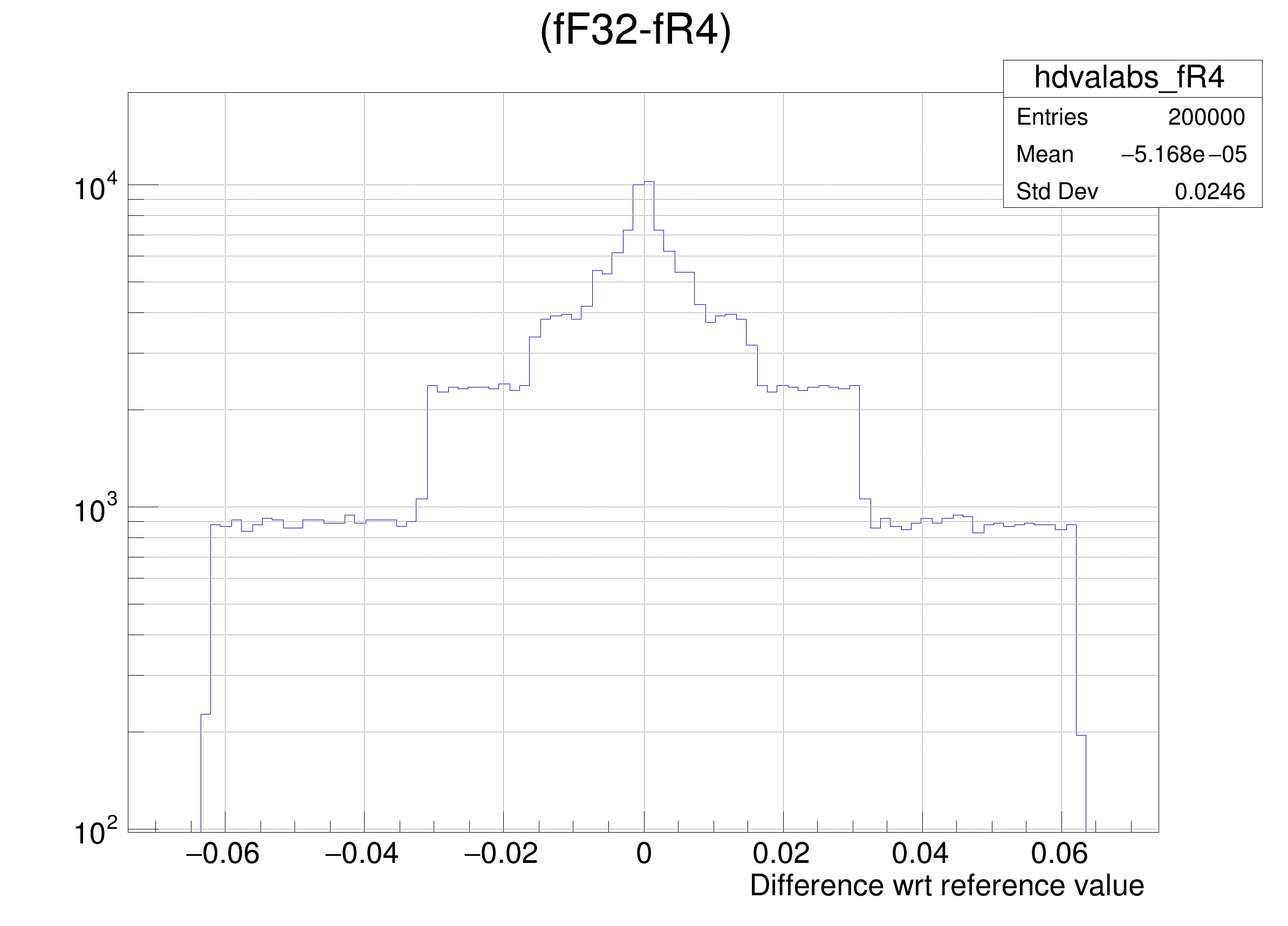
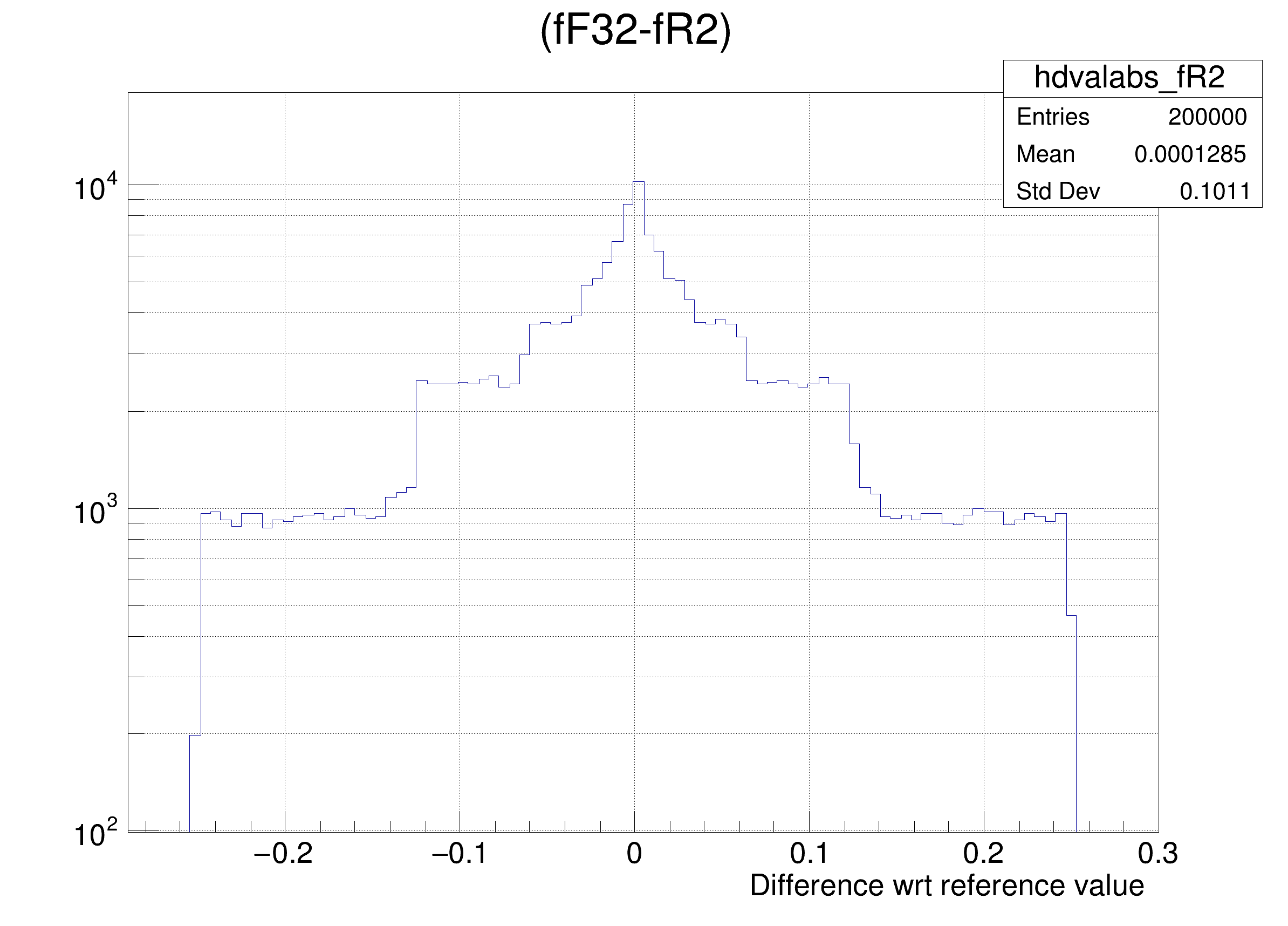
      tree.Draw(Form("(fF32-%s) >> hdvalabs_%s", brName, brName), "", "goff");
      auto hdval = gDirectory->Get<TH1F>(Form("hdvalabs_%s", brName));
      hdval->GetXaxis()->SetTitle("Difference wrt reference value");
      auto c = new TCanvas(brName, brName, 800, 600);
      c->SetGrid();
      c->SetLogy();
      hdval->DrawClone();
   }
 
   auto c1 = new TCanvas("c1", "c1", 800, 600);
   c1->SetGrid();
 
   h->Draw();
   h->GetXaxis()->LabelsOption("v");
   gcx->Draw("lp");
   gdrange->Draw("lp");
   gdval->Draw("lp");
 
   // Finally build a legend
   auto legend = new TLegend(0.3, 0.6, 0.9, 0.9);
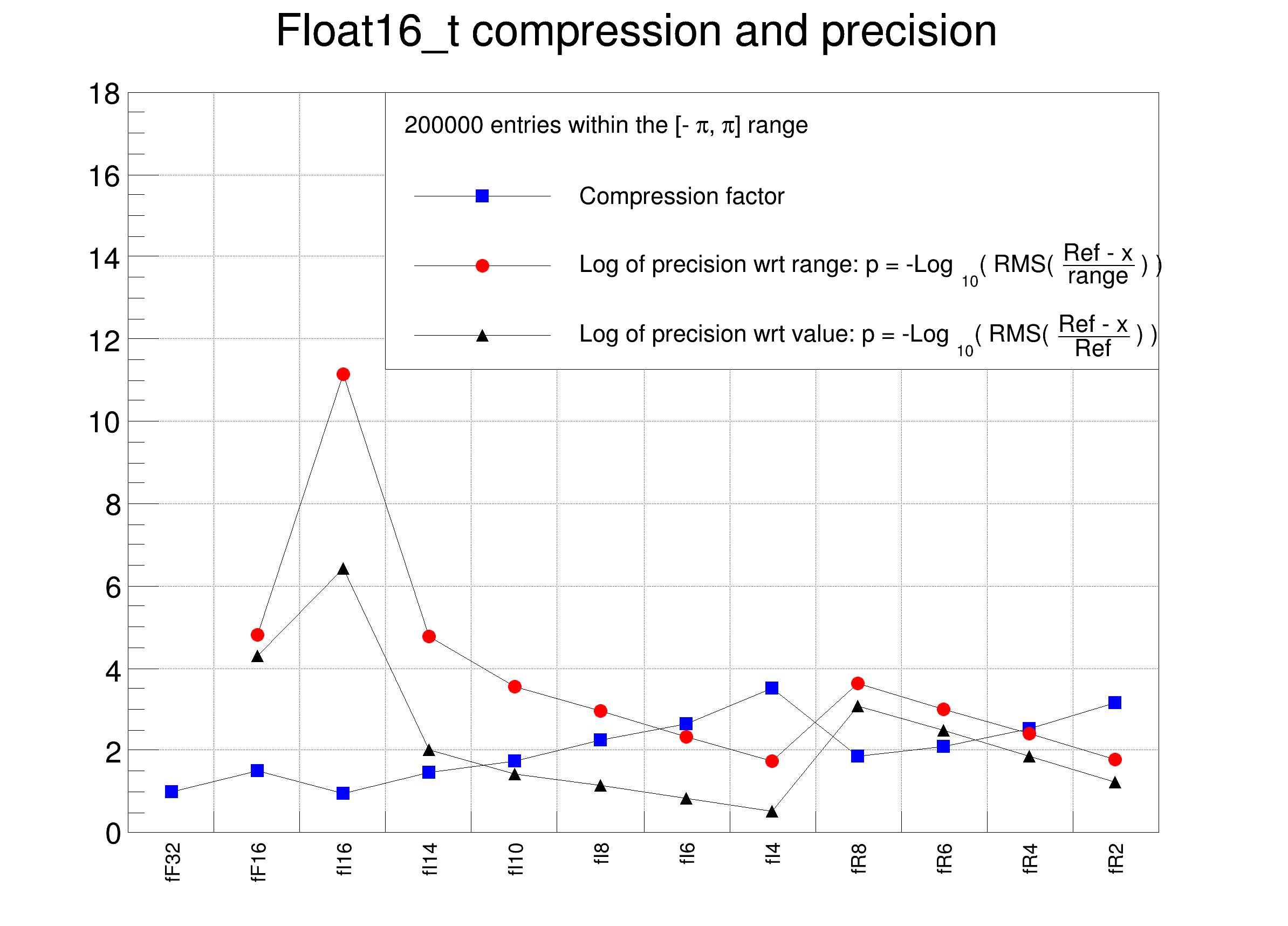
   legend->SetHeader(Form("%d entries within the [-#pi, #pi] range", nEntries));
   legend->AddEntry(gcx, "Compression factor", "lp");
   legend->AddEntry(gdrange, "Log of precision wrt range: p = -Log_{10}( RMS( #frac{Ref - x}{range} ) ) ", "lp");
   legend->AddEntry(gdval, "Log of precision wrt value: p = -Log_{10}( RMS( #frac{Ref - x}{Ref} ) ) ", "lp");
   legend->Draw();
}

Author

Danilo Piparo

Definition in file float16.C.