fit2a.C File Reference

Detailed Description

Fitting a 2-D histogram (a variant) This tutorial illustrates :

• how to create a 2-d function
• fill a 2-d histogram randomly from this function
• fit the histogram
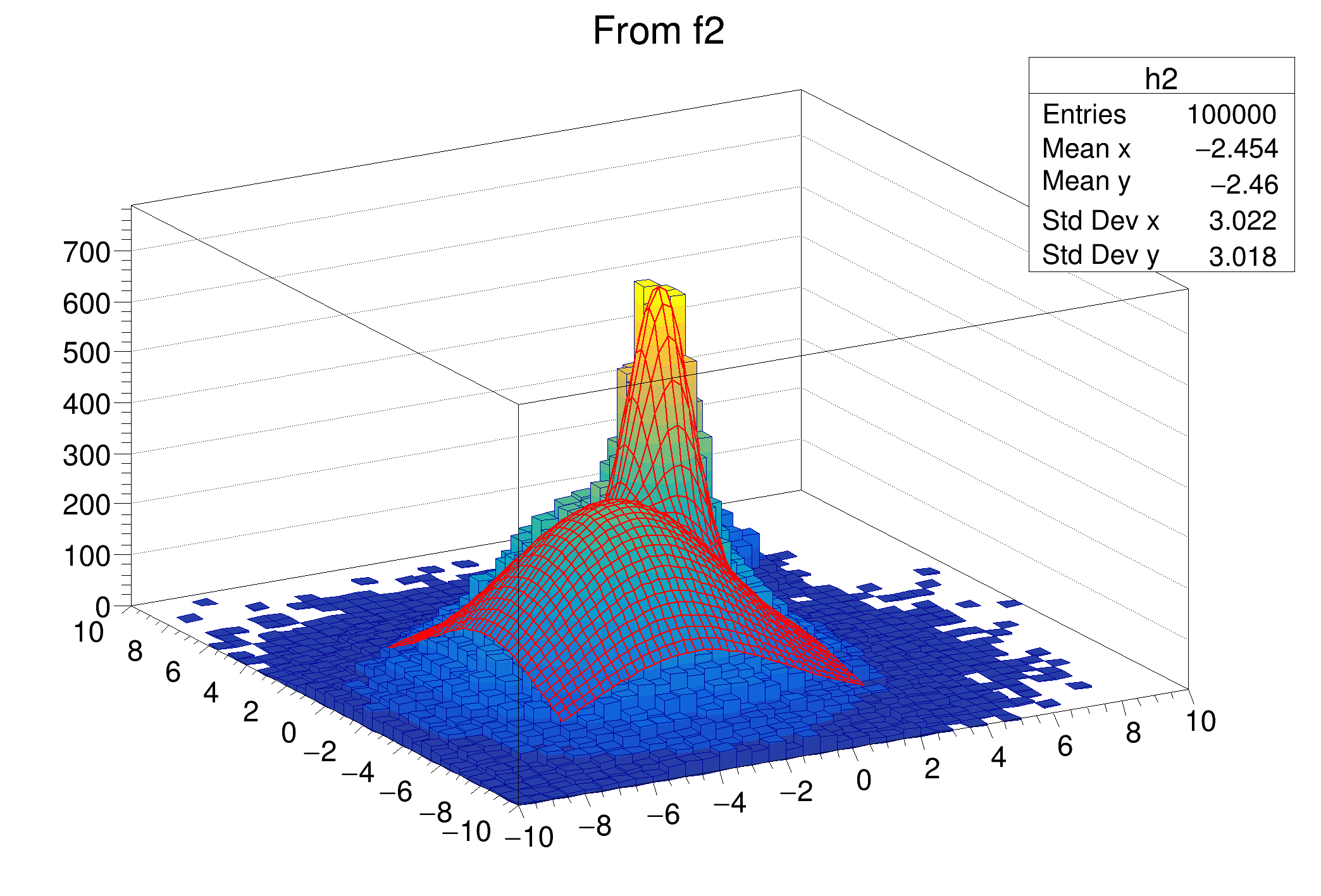
• display the fitted function on top of the histogram (lego-plot) using a surface plot in a sub-range of the histogram.

This example can be executed via the interpreter or/and the compiler

root > .x fit2a.C
root > .x fit2a.C++

 
 FCN=1048.29 FROM MIGRAD    STATUS=CONVERGED     384 CALLS         385 TOTAL
                     EDM=1.71323e-07    STRATEGY= 1  ERROR MATRIX UNCERTAINTY   1.7 per cent
  EXT PARAMETER                                   STEP         FIRST   
  NO.   NAME      VALUE            ERROR          SIZE      DERIVATIVE 
   1  p0           3.92557e+02   1.80794e+00  -8.93086e-04   1.08685e-04
   2  p1          -2.99839e+00   1.13352e-02  -6.49024e-06  -1.81171e-02
   3  p2           2.98485e+00   7.41044e-03   3.61030e-06  -5.86707e-02
   4  p3          -3.00202e+00   1.11595e-02  -5.78996e-06  -1.75293e-02
   5  p4           2.97271e+00   7.15832e-03  -3.28538e-06  -4.12677e-02
   6  p5           6.01136e+02   9.83774e+00   3.21497e-03  -2.69040e-05
   7  p6           6.14587e-03   1.13579e-02   5.13989e-06   2.41418e-02
   8  p7           8.16263e-01   9.52518e-03   3.01650e-06  -8.27896e-03
   9  p8          -7.76134e-04   1.27854e-02   5.13131e-06  -5.37304e-03
  10  p9           9.11281e-01   1.09052e-02  -6.70503e-06   2.34952e-02
  11  p10          1.46899e+02   4.66962e+00  -3.42267e-04   5.38648e-05
  12  p11          3.98822e+00   1.79131e-02   1.99376e-05   9.00611e-03
  13  p12          7.27558e-01   1.32237e-02  -2.78350e-06   5.94843e-03
  14  p13          4.02638e+00   1.71292e-02   4.21853e-06   5.32476e-03
  15  p14          7.03078e-01   1.29939e-02   1.10618e-06  -3.47421e-02
(TCanvas *) 0x55bcd6caa0f0

 
#include "TF2.h"
#include "TH2.h"
#include "TCutG.h"
#include "TMath.h"
#include "TCanvas.h"
#include "TStyle.h"
 
Double_t g2(Double_t *x, Double_t *par) {
   Double_t r1 = Double_t((x[0]-par[1])/par[2]);
   Double_t r2 = Double_t((x[1]-par[3])/par[4]);
   return par[0]*TMath::Exp(-0.5*(r1*r1+r2*r2));
}
Double_t fun2(Double_t *x, Double_t *par) {
   Double_t *p1 = &par[0];
   Double_t *p2 = &par[5];
   Double_t *p3 = &par[10];
   Double_t result = g2(x,p1) + g2(x,p2) + g2(x,p3);
   return result;
}
 
TCanvas *fit2a() {
   TCanvas *c = new TCanvas();
   gStyle->SetOptStat(kTRUE);
   gStyle->SetPalette(57);
   const Int_t npar = 15;
   Double_t f2params[npar] = {100,-3,3,-3,3,160,0,0.8,0,0.9,40,4,0.7,4,0.7};
   auto f2 = new TF2("f2",fun2,-10,10,-10,10, npar);
   f2->SetParameters(f2params);
 
   //Create an histogram and fill it randomly with f2
   auto h2 = new TH2F("h2","From f2",40,-10,10,40,-10,10);
   Int_t nentries = 100000;
   h2->FillRandom("f2",nentries);
   //Fit h2 with original function f2
   Float_t ratio = 4*nentries/100000;
   f2params[ 0] *= ratio;
   f2params[ 5] *= ratio;
   f2params[10] *= ratio;
   f2->SetParameters(f2params);
   h2->Fit("f2","N");
   auto cutg = new TCutG("cutg",5);
   cutg->SetPoint(0,-7,-7);
   cutg->SetPoint(1, 2,-7);
   cutg->SetPoint(2, 2, 2);
   cutg->SetPoint(3,-7, 2);
   cutg->SetPoint(4,-7,-7);
   h2->Draw("lego2 0");
   h2->SetFillColor(38);
   f2->SetNpx(80);
   f2->SetNpy(80);
   f2->Draw("surf1 same bb [cutg]");
   return c;
}

Author

Rene Brun

Definition in file fit2a.C.