rs_bernsteinCorrection.C File Reference

Detailed Description

Example of the BernsteinCorrection utility in RooStats.

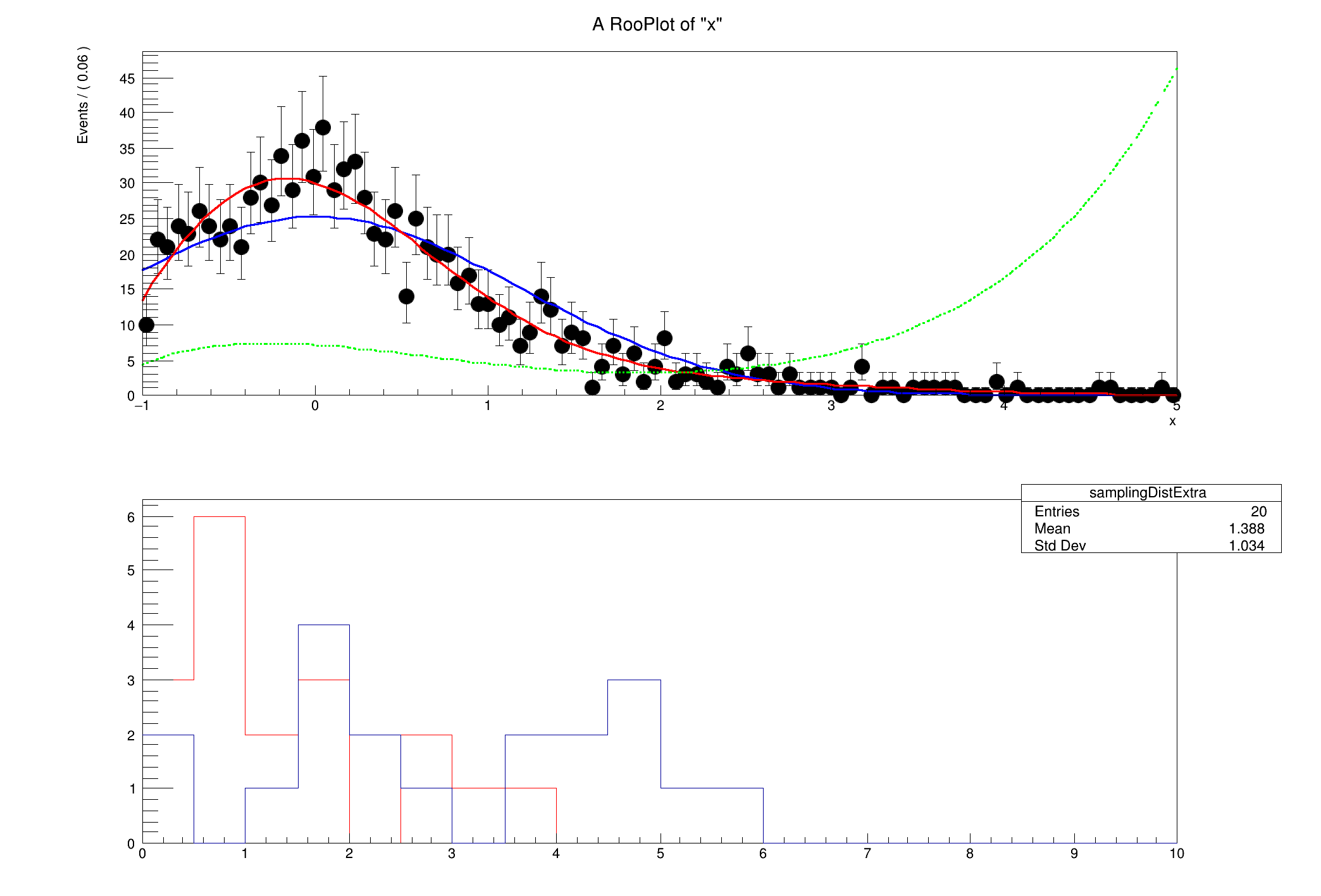
The idea is that one has a distribution coming either from data or Monte Carlo (called "reality" in the macro) and a nominal model that is not sufficiently flexible to take into account the real distribution. One wants to take into account the systematic associated with this imperfect modeling by augmenting the nominal model with some correction term (in this case a polynomial). The BernsteinCorrection utility will import into your workspace a corrected model given by nominal(x) * poly_N(x), where poly_N is an n-th order polynomial in the Bernstein basis. The degree N of the polynomial is chosen by specifying the tolerance one has in adding an extra term to the polynomial. The Bernstein basis is nice because it only has positive-definite terms and works well with PDFs. Finally, the macro makes a plot of:

• the data (drawn from 'reality'),
• the best fit of the nominal model (blue)
• and the best fit corrected model.

 
 
␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m 
                Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
                All rights reserved, please read http://roofit.sourceforge.net/license.txt
 
[#1] INFO:ObjectHandling -- RooWorkspace::import(myWorksspace) importing dataset realityData
[#1] INFO:ObjectHandling -- RooWorkSpace::import(myWorksspace) changing name of dataset from  realityData to data
[#1] INFO:ObjectHandling -- RooWorkspace::import(myWorksspace) importing RooRealVar::x
[#1] INFO:ObjectHandling -- RooWorkspace::import(myWorksspace) importing RooGaussian::nominal
[#1] INFO:ObjectHandling -- RooWorkspace::import(myWorksspace) importing RooConstVar::0
[#1] INFO:ObjectHandling -- RooWorkspace::import(myWorksspace) importing RooRealVar::sigma
BernsteinCorrection::ImportCorrectedPdf -  Doing initial Fit with nominal model 
[#1] INFO:Minization -- createNLL: caching constraint set under name CONSTR_OF_PDF_nominal_FOR_OBS_x with 0 entries
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(corrected_clone_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(corrected_clone_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(corrected_clone_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(corrected_clone_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(corrected_clone_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(corrected_clone_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:ObjectHandling -- RooWorkspace::import(myWorksspace) importing RooEffProd::corrected
[#1] INFO:ObjectHandling -- RooWorkspace::import(myWorksspace) importing RooBernstein::poly
[#1] INFO:ObjectHandling -- RooWorkspace::import(myWorksspace) importing RooRealVar::c_0
[#1] INFO:ObjectHandling -- RooWorkspace::import(myWorksspace) importing RooRealVar::c_1
[#1] INFO:ObjectHandling -- RooWorkspace::import(myWorksspace) importing RooRealVar::c_2
[#1] INFO:ObjectHandling -- RooWorkspace::import(myWorksspace) importing RooRealVar::c_3
[#1] INFO:ObjectHandling -- RooWorkspace::import(myWorksspace) importing RooRealVar::c_4
[#1] INFO:ObjectHandling -- RooWorkspace::import(myWorksspace) importing RooRealVar::c_5
[#1] INFO:ObjectHandling -- RooWorkspace::import(myWorksspace) importing RooRealVar::c_6
------ Begin Bernstein Correction Log --------
degree = 1 -log L(0) = 1216.78 -log L(1) = 1208.89 q = 15.7692 P(chi^2_1 > q) = 7.1557e-05
degree = 2 -log L(1) = 1208.89 -log L(2) = 1203.21 q = 11.3692 P(chi^2_1 > q) = 0.000746732
degree = 3 -log L(2) = 1203.21 -log L(3) = 1198.85 q = 8.72213 P(chi^2_1 > q) = 0.00314371
degree = 4 -log L(3) = 1198.85 -log L(4) = 1190.19 q = 17.3163 P(chi^2_1 > q) = 3.1646e-05
degree = 5 -log L(4) = 1190.19 -log L(5) = 1183.56 q = 13.259 P(chi^2_1 > q) = 0.00027127
degree = 6 -log L(5) = 1183.56 -log L(6) = 1182.57 q = 1.98376 P(chi^2_1 > q) = 0.158995
------ End Bernstein Correction Log --------
 Correction based on Bernstein Poly of degree 6
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
Minuit2Minimizer: Minimize with max-calls 500 convergence for edm < 1 strategy 1
Minuit2Minimizer : Valid minimum - status = 0
FVAL  = 1216.77793416266263
Edm   = 4.16187321843267985e-07
Nfcn  = 19
sigma   = 1.18138  +/-  0.0315451   (limited)
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(corrected_clone_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
[#1] INFO:Minization -- createNLL: caching constraint set under name CONSTR_OF_PDF_corrected_FOR_OBS_x with 0 entries
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
Minuit2Minimizer: Minimize with max-calls 3500 convergence for edm < 1 strategy 1
Minuit2Minimizer : Valid minimum - status = 0
FVAL  = 1182.56771140342289
Edm   = 0.000104058539332425995
Nfcn  = 184
c_1     = 3.18369  +/-  0.83541  (limited)
c_2     = 1.25333e-05    +/-  3.09835  (limited)
c_3     = 1.62863e-06    +/-  1.52587  (limited)
c_4     = 0.971397    +/-  2.53146  (limited)
c_5     = 0.199979    +/-  75.676   (limited)
c_6     = 10.5075  +/-  23.0146  (limited)
sigma   = 1.26617  +/-  0.232486 (limited)
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(corrected_clone_Int[x]) using numeric integrator RooIntegrator1D to calculate Int(x)
made pdfs, make toy generator
on toy 0
on toy 1
on toy 2
on toy 3
on toy 4
on toy 5
on toy 6
on toy 7
on toy 8
on toy 9
on toy 10
on toy 11
on toy 12
on toy 13
on toy 14
on toy 15
on toy 16
on toy 17
on toy 18
on toy 19

 
#include "RooDataSet.h"
#include "RooRealVar.h"
#include "RooConstVar.h"
#include "RooBernstein.h"
#include "TCanvas.h"
#include "RooAbsPdf.h"
#include "RooFit.h"
#include "RooFitResult.h"
#include "RooPlot.h"
#include <string>
#include <vector>
#include <stdio.h>
#include <sstream>
#include <iostream>
 
#include "RooProdPdf.h"
#include "RooAddPdf.h"
#include "RooGaussian.h"
#include "RooNLLVar.h"
#include "RooMinuit.h"
#include "RooProfileLL.h"
#include "RooWorkspace.h"
 
#include "RooStats/BernsteinCorrection.h"
 
// use this order for safety on library loading
using namespace RooFit;
using namespace RooStats;
 
//____________________________________
void rs_bernsteinCorrection()
{
 
   // set range of observable
   Double_t lowRange = -1, highRange = 5;
 
   // make a RooRealVar for the observable
   RooRealVar x("x", "x", lowRange, highRange);
 
   // true model
   RooGaussian narrow("narrow", "", x, RooConst(0.), RooConst(.8));
   RooGaussian wide("wide", "", x, RooConst(0.), RooConst(2.));
   RooAddPdf reality("reality", "", RooArgList(narrow, wide), RooConst(0.8));
 
   RooDataSet *data = reality.generate(x, 1000);
 
   // nominal model
   RooRealVar sigma("sigma", "", 1., 0, 10);
   RooGaussian nominal("nominal", "", x, RooConst(0.), sigma);
 
   RooWorkspace *wks = new RooWorkspace("myWorksspace");
 
   wks->import(*data, Rename("data"));
   wks->import(nominal);
 
   if (TClass::GetClass("ROOT::Minuit2::Minuit2Minimizer")) {
      // use Minuit2 if ROOT was built with support for it:
      ROOT::Math::MinimizerOptions::SetDefaultMinimizer("Minuit2");
   }
 
   // The tolerance sets the probability to add an unnecessary term.
   // lower tolerance will add fewer terms, while higher tolerance
   // will add more terms and provide a more flexible function.
   Double_t tolerance = 0.05;
   BernsteinCorrection bernsteinCorrection(tolerance);
   Int_t degree = bernsteinCorrection.ImportCorrectedPdf(wks, "nominal", "x", "data");
 
   if (degree < 0) {
      Error("rs_bernsteinCorrection", "Bernstein correction failed ! ");
      return;
   }
 
   cout << " Correction based on Bernstein Poly of degree " << degree << endl;
 
   RooPlot *frame = x.frame();
   data->plotOn(frame);
   // plot the best fit nominal model in blue
   TString minimType = ROOT::Math::MinimizerOptions::DefaultMinimizerType();
   nominal.fitTo(*data, PrintLevel(0), Minimizer(minimType));
   nominal.plotOn(frame);
 
   // plot the best fit corrected model in red
   RooAbsPdf *corrected = wks->pdf("corrected");
   if (!corrected)
      return;
 
   // fit corrected model
   corrected->fitTo(*data, PrintLevel(0), Minimizer(minimType));
   corrected->plotOn(frame, LineColor(kRed));
 
   // plot the correction term (* norm constant) in dashed green
   // should make norm constant just be 1, not depend on binning of data
   RooAbsPdf *poly = wks->pdf("poly");
   if (poly)
      poly->plotOn(frame, LineColor(kGreen), LineStyle(kDashed));
 
   // this is a switch to check the sampling distribution
   // of -2 log LR for two comparisons:
   // the first is for n-1 vs. n degree polynomial corrections
   // the second is for n vs. n+1 degree polynomial corrections
   // Here we choose n to be the one chosen by the tolerance
   // criterion above, eg. n = "degree" in the code.
   // Setting this to true is takes about 10 min.
   bool checkSamplingDist = true;
   int numToyMC = 20; // increase this value for sensible results
 
   TCanvas *c1 = new TCanvas();
   if (checkSamplingDist) {
      c1->Divide(1, 2);
      c1->cd(1);
   }
   frame->Draw();
   gPad->Update();
 
   if (checkSamplingDist) {
      // check sampling dist
      ROOT::Math::MinimizerOptions::SetDefaultPrintLevel(-1);
      TH1F *samplingDist = new TH1F("samplingDist", "", 20, 0, 10);
      TH1F *samplingDistExtra = new TH1F("samplingDistExtra", "", 20, 0, 10);
      bernsteinCorrection.CreateQSamplingDist(wks, "nominal", "x", "data", samplingDist, samplingDistExtra, degree,
                                              numToyMC);
 
      c1->cd(2);
      samplingDistExtra->SetLineColor(kRed);
      samplingDistExtra->Draw();
      samplingDist->Draw("same");
   }
}

Author

Kyle Cranmer

Definition in file rs_bernsteinCorrection.C.