Logo ROOT   6.18/05
Reference Guide
rf607_fitresult.C File Reference
Tutorials » RooFit Tutorials

Detailed Description

View in nbviewer Open in SWAN Likelihood and minimization: demonstration of options of the RooFitResult class

␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m
Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
All rights reserved, please read http://roofit.sourceforge.net/license.txt
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
[#1] INFO:Minization -- The following expressions will be evaluated in cache-and-track mode: (bkg,sig1,sig2)
**********
** 1 **SET PRINT 1
**********
**********
** 2 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 a0 5.00000e-01 1.00000e-01 0.00000e+00 1.00000e+00
2 bkgfrac 5.00000e-01 1.00000e-01 0.00000e+00 1.00000e+00
3 mean 5.00000e+00 2.00000e+00 -1.00000e+01 1.00000e+01
4 sig1frac 8.00000e-01 1.00000e-01 0.00000e+00 1.00000e+00
5 sigma1 5.00000e-01 2.00000e-01 1.00000e-01 1.00000e+01
6 sigma2 1.00000e+00 4.50000e-01 1.00000e-01 1.00000e+01
**********
** 3 **SET ERR 0.5
**********
**********
** 4 **SET PRINT 1
**********
**********
** 5 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 6 **MIGRAD 3000 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
FCN=1890.61 FROM MIGRAD STATUS=INITIATE 20 CALLS 21 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a0 5.00000e-01 1.00000e-01 2.01358e-01 -1.79143e+01
2 bkgfrac 5.00000e-01 1.00000e-01 2.01358e-01 8.01836e+00
3 mean 5.00000e+00 2.00000e+00 2.35352e-01 -3.18732e+02
4 sig1frac 8.00000e-01 1.00000e-01 2.57889e-01 1.67753e+00
5 sigma1 5.00000e-01 2.00000e-01 1.06123e-01 -2.80511e+01
6 sigma2 1.00000e+00 4.50000e-01 1.63378e-01 -2.79262e+00
ERR DEF= 0.5
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=1885.34 FROM MIGRAD STATUS=CONVERGED 177 CALLS 178 TOTAL
EDM=0.000199951 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 a0 7.28245e-01 1.10053e-01 4.01494e-03 -5.30986e-04
2 bkgfrac 4.34386e-01 8.18255e-02 1.44990e-03 -2.37203e-02
3 mean 5.03463e+00 3.36192e-02 1.15677e-04 -1.36017e-01
4 sig1frac 7.78347e-01 9.66774e-02 3.39065e-03 -2.60523e-02
5 sigma1 5.23396e-01 4.47433e-02 4.30203e-04 -2.02274e-01
6 sigma2 1.77668e+00 1.13135e+00 3.09140e-03 2.51106e-02
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 6 ERR DEF=0.5
1.237e-02 -7.217e-03 -1.043e-04 -4.043e-03 1.989e-03 1.052e-01
-7.217e-03 6.757e-03 -1.369e-04 4.830e-03 -1.372e-03 -8.173e-02
-1.043e-04 -1.369e-04 1.130e-03 -2.833e-04 -6.480e-05 3.890e-04
-4.043e-03 4.830e-03 -2.833e-04 9.520e-03 1.344e-03 -2.831e-02
1.989e-03 -1.372e-03 -6.480e-05 1.344e-03 2.002e-03 2.936e-02
1.052e-01 -8.173e-02 3.890e-04 -2.831e-02 2.936e-02 1.322e+00
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2 3 4 5 6
1 0.84288 1.000 -0.790 -0.028 -0.373 0.400 0.823
2 0.95650 -0.790 1.000 -0.050 0.602 -0.373 -0.865
3 0.13243 -0.028 -0.050 1.000 -0.086 -0.043 0.010
4 0.87689 -0.373 0.602 -0.086 1.000 0.308 -0.252
5 0.76698 0.400 -0.373 -0.043 0.308 1.000 0.571
6 0.94237 0.823 -0.865 0.010 -0.252 0.571 1.000
**********
** 7 **SET ERR 0.5
**********
**********
** 8 **SET PRINT 1
**********
**********
** 9 **HESSE 3000
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=1885.34 FROM HESSE STATUS=OK 40 CALLS 218 TOTAL
EDM=0.000205499 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 a0 7.28245e-01 1.11109e-01 1.60598e-04 4.74047e-01
2 bkgfrac 4.34386e-01 8.36079e-02 2.89981e-04 -1.31608e-01
3 mean 5.03463e+00 3.36219e-02 2.31353e-05 5.27602e-01
4 sig1frac 7.78347e-01 9.69912e-02 6.78131e-04 5.90402e-01
5 sigma1 5.23396e-01 4.51307e-02 8.60406e-05 -1.15419e+00
6 sigma2 1.77668e+00 1.15533e+00 6.18281e-04 -7.22519e-01
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 6 ERR DEF=0.5
1.261e-02 -7.502e-03 -9.635e-05 -4.154e-03 2.084e-03 1.091e-01
-7.502e-03 7.058e-03 -1.441e-04 4.954e-03 -1.470e-03 -8.595e-02
-9.635e-05 -1.441e-04 1.130e-03 -2.873e-04 -6.383e-05 4.916e-04
-4.154e-03 4.954e-03 -2.873e-04 9.583e-03 1.310e-03 -3.000e-02
2.084e-03 -1.470e-03 -6.383e-05 1.310e-03 2.037e-03 3.075e-02
1.091e-01 -8.595e-02 4.916e-04 -3.000e-02 3.075e-02 1.380e+00
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2 3 4 5 6
1 0.84619 1.000 -0.795 -0.026 -0.378 0.411 0.827
2 0.95839 -0.795 1.000 -0.051 0.602 -0.388 -0.871
3 0.13303 -0.026 -0.051 1.000 -0.087 -0.042 0.012
4 0.87775 -0.378 0.602 -0.087 1.000 0.297 -0.261
5 0.77155 0.411 -0.388 -0.042 0.297 1.000 0.580
6 0.94489 0.827 -0.871 0.012 -0.261 0.580 1.000
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
RooFitResult: minimized FCN value: 1885.34, estimated distance to minimum: 0.000205499
covariance matrix quality: Full, accurate covariance matrix
Status : MINIMIZE=0 HESSE=0
Floating Parameter FinalValue +/- Error
-------------------- --------------------------
a0 7.2825e-01 +/- 1.11e-01
bkgfrac 4.3439e-01 +/- 8.36e-02
mean 5.0346e+00 +/- 3.36e-02
sig1frac 7.7835e-01 +/- 9.70e-02
sigma1 5.2340e-01 +/- 4.51e-02
sigma2 1.7767e+00 +/- 1.16e+00
RooFitResult: minimized FCN value: 1885.34, estimated distance to minimum: 0.000205499
covariance matrix quality: Full, accurate covariance matrix
Status : MINIMIZE=0 HESSE=0
Constant Parameter Value
-------------------- ------------
a1 -2.0000e-01
Floating Parameter InitialValue FinalValue +/- Error GblCorr.
-------------------- ------------ -------------------------- --------
a0 5.0000e-01 7.2825e-01 +/- 1.11e-01 <none>
bkgfrac 5.0000e-01 4.3439e-01 +/- 8.36e-02 <none>
mean 5.0000e+00 5.0346e+00 +/- 3.36e-02 <none>
sig1frac 8.0000e-01 7.7835e-01 +/- 9.70e-02 <none>
sigma1 5.0000e-01 5.2340e-01 +/- 4.51e-02 <none>
sigma2 1.0000e+00 1.7767e+00 +/- 1.16e+00 <none>
EDM = 0.000205499
-log(L) at minimum = 1885.34
final value of floating parameters
1) RooRealVar:: a0 = 0.728245 +/- 0.111109
2) RooRealVar:: bkgfrac = 0.434386 +/- 0.0836079
3) RooRealVar:: mean = 5.03463 +/- 0.0336219
4) RooRealVar:: sig1frac = 0.778347 +/- 0.0969912
5) RooRealVar:: sigma1 = 0.523396 +/- 0.0451307
6) RooRealVar:: sigma2 = 1.77668 +/- 1.15533
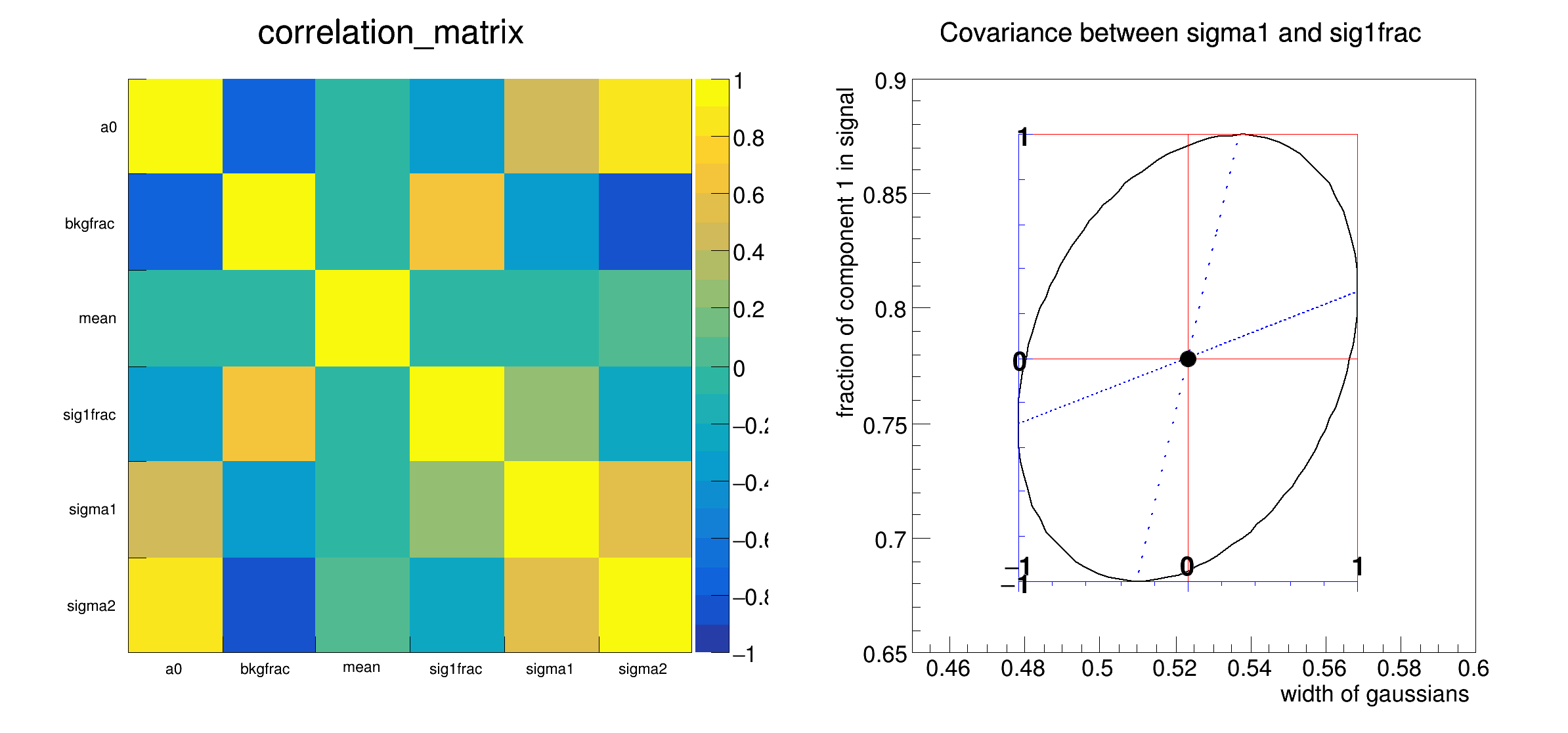
correlation between sig1frac and a0 is -0.377851
correlation between bkgfrac and mean is -0.0510232
correlation matrix
6x6 matrix is as follows
| 0 | 1 | 2 | 3 | 4 |
----------------------------------------------------------------------
0 | 1 -0.7952 -0.02552 -0.3779 0.4111
1 | -0.7952 1 -0.05102 0.6023 -0.3876
2 | -0.02552 -0.05102 1 -0.0873 -0.04206
3 | -0.3779 0.6023 -0.0873 1 0.2966
4 | 0.4111 -0.3876 -0.04206 0.2966 1
5 | 0.8272 -0.8708 0.01245 -0.2609 0.5799
| 5 |
----------------------------------------------------------------------
0 | 0.8272
1 | -0.8708
2 | 0.01245
3 | -0.2609
4 | 0.5799
5 | 1
covariance matrix
6x6 matrix is as follows
| 0 | 1 | 2 | 3 | 4 |
----------------------------------------------------------------------
0 | 0.01261 -0.007502 -9.635e-05 -0.004154 0.002084
1 | -0.007502 0.007058 -0.0001441 0.004954 -0.00147
2 | -9.635e-05 -0.0001441 0.00113 -0.0002873 -6.383e-05
3 | -0.004154 0.004954 -0.0002873 0.009583 0.00131
4 | 0.002084 -0.00147 -6.383e-05 0.00131 0.002037
5 | 0.1091 -0.08595 0.0004916 -0.03 0.03075
| 5 |
----------------------------------------------------------------------
0 | 0.1091
1 | -0.08595
2 | 0.0004916
3 | -0.03
4 | 0.03075
5 | 1.38
#include "RooRealVar.h"
#include "RooDataSet.h"
#include "RooGaussian.h"
#include "RooConstVar.h"
#include "RooAddPdf.h"
#include "RooChebychev.h"
#include "RooFitResult.h"
#include "TCanvas.h"
#include "TAxis.h"
#include "RooPlot.h"
#include "TFile.h"
#include "TStyle.h"
#include "TH2.h"
#include "TMatrixDSym.h"
using namespace RooFit;
void rf607_fitresult()
{
// C r e a t e p d f , d a t a
// --------------------------------
// Declare observable x
RooRealVar x("x", "x", 0, 10);
// Create two Gaussian PDFs g1(x,mean1,sigma) anf g2(x,mean2,sigma) and their parameters
RooRealVar mean("mean", "mean of gaussians", 5, -10, 10);
RooRealVar sigma1("sigma1", "width of gaussians", 0.5, 0.1, 10);
RooRealVar sigma2("sigma2", "width of gaussians", 1, 0.1, 10);
RooGaussian sig1("sig1", "Signal component 1", x, mean, sigma1);
RooGaussian sig2("sig2", "Signal component 2", x, mean, sigma2);
// Build Chebychev polynomial p.d.f.
RooRealVar a0("a0", "a0", 0.5, 0., 1.);
RooRealVar a1("a1", "a1", -0.2);
RooChebychev bkg("bkg", "Background", x, RooArgSet(a0, a1));
// Sum the signal components into a composite signal p.d.f.
RooRealVar sig1frac("sig1frac", "fraction of component 1 in signal", 0.8, 0., 1.);
RooAddPdf sig("sig", "Signal", RooArgList(sig1, sig2), sig1frac);
// Sum the composite signal and background
RooRealVar bkgfrac("bkgfrac", "fraction of background", 0.5, 0., 1.);
RooAddPdf model("model", "g1+g2+a", RooArgList(bkg, sig), bkgfrac);
// Generate 1000 events
RooDataSet *data = model.generate(x, 1000);
// F i t p d f t o d a t a , s a v e f i t r e s u l t
// -------------------------------------------------------------
// Perform fit and save result
RooFitResult *r = model.fitTo(*data, Save());
// P r i n t f i t r e s u l t s
// ---------------------------------
// Summary printing: Basic info plus final values of floating fit parameters
r->Print();
// Verbose printing: Basic info, values of constant parameters, initial and
// final values of floating parameters, global correlations
r->Print("v");
// V i s u a l i z e c o r r e l a t i o n m a t r i x
// -------------------------------------------------------
// Construct 2D color plot of correlation matrix
gStyle->SetOptStat(0);
TH2 *hcorr = r->correlationHist();
// Visualize ellipse corresponding to single correlation matrix element
RooPlot *frame = new RooPlot(sigma1, sig1frac, 0.45, 0.60, 0.65, 0.90);
frame->SetTitle("Covariance between sigma1 and sig1frac");
r->plotOn(frame, sigma1, sig1frac, "ME12ABHV");
// A c c e s s f i t r e s u l t i n f o r m a t i o n
// ---------------------------------------------------------
// Access basic information
cout << "EDM = " << r->edm() << endl;
cout << "-log(L) at minimum = " << r->minNll() << endl;
// Access list of final fit parameter values
cout << "final value of floating parameters" << endl;
r->floatParsFinal().Print("s");
// Access correlation matrix elements
cout << "correlation between sig1frac and a0 is " << r->correlation(sig1frac, a0) << endl;
cout << "correlation between bkgfrac and mean is " << r->correlation("bkgfrac", "mean") << endl;
// Extract covariance and correlation matrix as TMatrixDSym
const TMatrixDSym &cor = r->correlationMatrix();
const TMatrixDSym &cov = r->covarianceMatrix();
// Print correlation, covariance matrix
cout << "correlation matrix" << endl;
cor.Print();
cout << "covariance matrix" << endl;
cov.Print();
// P e r s i s t f i t r e s u l t i n r o o t f i l e
// -------------------------------------------------------------
// Open new ROOT file save save result
TFile f("rf607_fitresult.root", "RECREATE");
r->Write("rf607");
f.Close();
// In a clean ROOT session retrieve the persisted fit result as follows:
// RooFitResult* r = gDirectory->Get("rf607") ;
TCanvas *c = new TCanvas("rf607_fitresult", "rf607_fitresult", 800, 400);
c->Divide(2);
c->cd(1);
gPad->SetLeftMargin(0.15);
hcorr->GetYaxis()->SetTitleOffset(1.4);
hcorr->Draw("colz");
c->cd(2);
gPad->SetLeftMargin(0.15);
frame->GetYaxis()->SetTitleOffset(1.6);
frame->Draw();
}
r
ROOT::R::TRInterface & r
Definition: Object.C:4
f
#define f(i)
Definition: RSha256.hxx:104
c
#define c(i)
Definition: RSha256.hxx:101
gStyle
R__EXTERN TStyle * gStyle
Definition: TStyle.h:406
gPad
#define gPad
Definition: TVirtualPad.h:286
RooAddPdf
RooAddPdf is an efficient implementation of a sum of PDFs of the form.
Definition: RooAddPdf.h:29
RooArgList
RooArgList is a container object that can hold multiple RooAbsArg objects.
Definition: RooArgList.h:21
RooArgSet
RooArgSet is a container object that can hold multiple RooAbsArg objects.
Definition: RooArgSet.h:28
RooChebychev
Chebychev polynomial p.d.f.
Definition: RooChebychev.h:25
RooDataSet
RooDataSet is a container class to hold unbinned data.
Definition: RooDataSet.h:31
RooFitResult
RooFitResult is a container class to hold the input and output of a PDF fit to a dataset.
Definition: RooFitResult.h:40
RooGaussian
Plain Gaussian p.d.f.
Definition: RooGaussian.h:25
RooPlot
A RooPlot is a plot frame and a container for graphics objects within that frame.
Definition: RooPlot.h:41
RooPlot::SetTitle
void SetTitle(const char *name)
Set the title of the RooPlot to 'title'.
Definition: RooPlot.cxx:1104
RooPlot::GetYaxis
TAxis * GetYaxis() const
Definition: RooPlot.cxx:1123
RooPlot::Draw
virtual void Draw(Option_t *options=0)
Draw this plot and all of the elements it contains.
Definition: RooPlot.cxx:558
RooRealVar
RooRealVar represents a fundamental (non-derived) real valued object.
Definition: RooRealVar.h:36
TAttAxis::SetTitleOffset
virtual void SetTitleOffset(Float_t offset=1)
Set distance between the axis and the axis title Offset is a correction factor with respect to the "s...
Definition: TAttAxis.cxx:294
TCanvas
The Canvas class.
Definition: TCanvas.h:31
TFile
A ROOT file is a suite of consecutive data records (TKey instances) with a well defined format.
Definition: TFile.h:48
TH1::GetYaxis
TAxis * GetYaxis()
Definition: TH1.h:317
TH1::Draw
virtual void Draw(Option_t *option="")
Draw this histogram with options.
Definition: TH1.cxx:2981
TH2
Service class for 2-Dim histogram classes.
Definition: TH2.h:30
TMatrixTBase::Print
void Print(Option_t *name="") const
Print the matrix as a table of elements.
Definition: TMatrixTBase.cxx:832
TObject::Write
virtual Int_t Write(const char *name=0, Int_t option=0, Int_t bufsize=0)
Write this object to the current directory.
Definition: TObject.cxx:785
TObject::Print
virtual void Print(Option_t *option="") const
This method must be overridden when a class wants to print itself.
Definition: TObject.cxx:550
TStyle::SetOptStat
void SetOptStat(Int_t stat=1)
The type of information printed in the histogram statistics box can be selected via the parameter mod...
Definition: TStyle.cxx:1444
x
Double_t x[n]
Definition: legend1.C:17
RooFit
Template specialisation used in RooAbsArg:
Definition: RooCFunction1Binding.h:29
RooFit::Save
RooCmdArg Save(Bool_t flag=kTRUE)
Definition: RooGlobalFunc.cxx:184
rf607_fitresult
Definition: rf607_fitresult.py:1
Author
07/2008 - Wouter Verkerke

Definition in file rf607_fitresult.C.