rf308_normintegration2d.C File Reference

Detailed Description

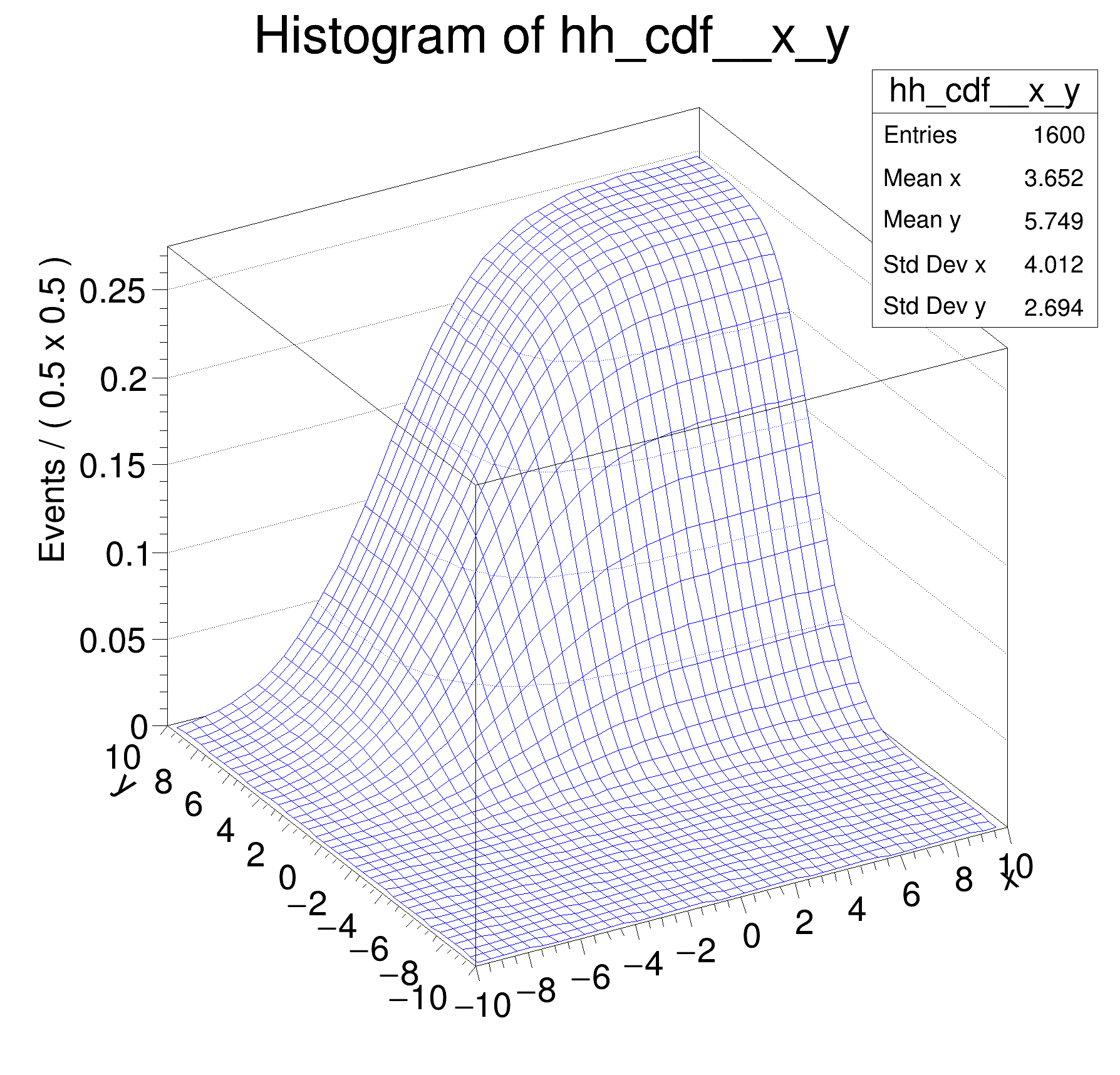
Multidimensional models: normalization and integration of p.d.fs, construction of cumulative distribution functions from p.d.f.s in two dimensions

 
 
␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m 
                Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
                All rights reserved, please read http://roofit.sourceforge.net/license.txt
 
gxy = 0.485672
gx_Norm[x,y] = 0.0129332
gx_Int[x,y] = 37.5523
gx_Norm[x] = 0.106896
gx_Norm[y] = 0.120989
[#1] INFO:Eval -- RooRealVar::setRange(x) new range named 'signal' created with bounds [-5,5]
[#1] INFO:Eval -- RooRealVar::setRange(y) new range named 'signal' created with bounds [-3,3]
gx_Int[x,y|signal]_Norm[x,y] = 0.572035
[#0] WARNING:InputArguments -- RooAbsReal::createHistogram(gxy_cdf_Int[x_prime,y_prime|CDF]_Norm[x_prime,y_prime]) WARNING extended mode requested for a non-pdf object, ignored

 
#include "RooRealVar.h"
#include "RooGaussian.h"
#include "RooConstVar.h"
#include "RooProdPdf.h"
#include "RooAbsReal.h"
#include "RooPlot.h"
#include "TCanvas.h"
#include "TAxis.h"
#include "TH1.h"
using namespace RooFit;
 
void rf308_normintegration2d()
{
   // S e t u p   m o d e l
   // ---------------------
 
   // Create observables x,y
   RooRealVar x("x", "x", -10, 10);
   RooRealVar y("y", "y", -10, 10);
 
   // Create p.d.f. gaussx(x,-2,3), gaussy(y,2,2)
   RooGaussian gx("gx", "gx", x, RooConst(-2), RooConst(3));
   RooGaussian gy("gy", "gy", y, RooConst(+2), RooConst(2));
 
   // Create gxy = gx(x)*gy(y)
   RooProdPdf gxy("gxy", "gxy", RooArgSet(gx, gy));
 
   // R e t r i e v e   r a w  &   n o r m a l i z e d   v a l u e s   o f   R o o F i t   p . d . f . s
   // --------------------------------------------------------------------------------------------------
 
   // Return 'raw' unnormalized value of gx
   cout << "gxy = " << gxy.getVal() << endl;
 
   // Return value of gxy normalized over x _and_ y in range [-10,10]
   RooArgSet nset_xy(x, y);
   cout << "gx_Norm[x,y] = " << gxy.getVal(&nset_xy) << endl;
 
   // Create object representing integral over gx
   // which is used to calculate  gx_Norm[x,y] == gx / gx_Int[x,y]
   RooAbsReal *igxy = gxy.createIntegral(RooArgSet(x, y));
   cout << "gx_Int[x,y] = " << igxy->getVal() << endl;
 
   // NB: it is also possible to do the following
 
   // Return value of gxy normalized over x in range [-10,10] (i.e. treating y as parameter)
   RooArgSet nset_x(x);
   cout << "gx_Norm[x] = " << gxy.getVal(&nset_x) << endl;
 
   // Return value of gxy normalized over y in range [-10,10] (i.e. treating x as parameter)
   RooArgSet nset_y(y);
   cout << "gx_Norm[y] = " << gxy.getVal(&nset_y) << endl;
 
   // I n t e g r a t e   n o r m a l i z e d   p d f   o v e r   s u b r a n g e
   // ----------------------------------------------------------------------------
 
   // Define a range named "signal" in x from -5,5
   x.setRange("signal", -5, 5);
   y.setRange("signal", -3, 3);
 
   // Create an integral of gxy_Norm[x,y] over x and y in range "signal"
   // This is the fraction of of p.d.f. gxy_Norm[x,y] which is in the
   // range named "signal"
   RooAbsReal *igxy_sig = gxy.createIntegral(RooArgSet(x, y), NormSet(RooArgSet(x, y)), Range("signal"));
   cout << "gx_Int[x,y|signal]_Norm[x,y] = " << igxy_sig->getVal() << endl;
 
   // C o n s t r u c t   c u m u l a t i v e   d i s t r i b u t i o n   f u n c t i o n   f r o m   p d f
   // -----------------------------------------------------------------------------------------------------
 
   // Create the cumulative distribution function of gx
   // i.e. calculate Int[-10,x] gx(x') dx'
   RooAbsReal *gxy_cdf = gxy.createCdf(RooArgSet(x, y));
 
   // Plot cdf of gx versus x
   TH1 *hh_cdf = gxy_cdf->createHistogram("hh_cdf", x, Binning(40), YVar(y, Binning(40)));
   hh_cdf->SetLineColor(kBlue);
 
   new TCanvas("rf308_normintegration2d", "rf308_normintegration2d", 600, 600);
   gPad->SetLeftMargin(0.15);
   hh_cdf->GetZaxis()->SetTitleOffset(1.8);
   hh_cdf->Draw("surf");
}

Author

07/2008 - Wouter Verkerke

Definition in file rf308_normintegration2d.C.