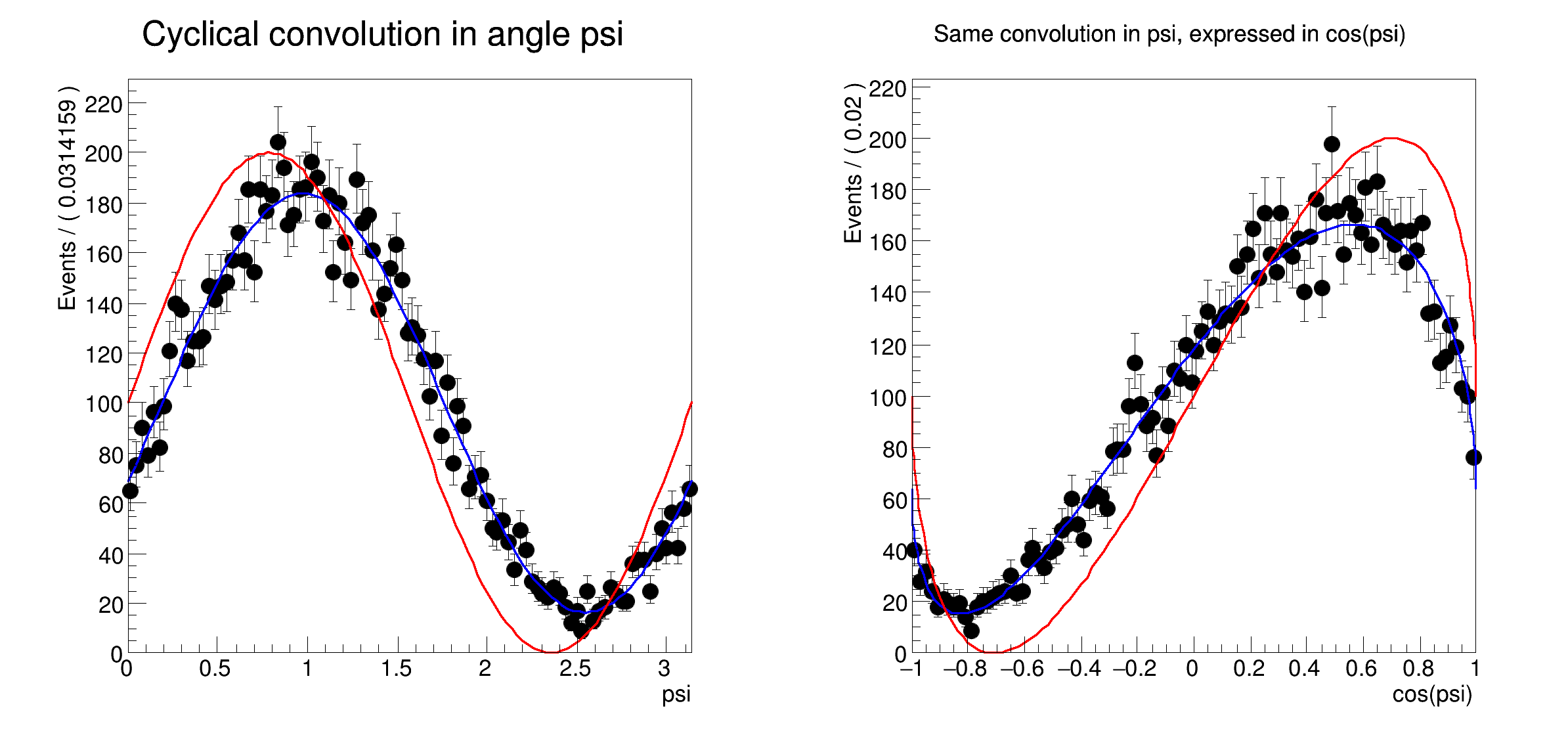
and construction of p.d.f in terms of transformed angular coordinates, e.g. cos(theta), where the convolution is performed in theta rather than cos(theta)
pdf(theta) = T(theta) (x) gauss(theta) pdf(cosTheta) = T(acos(cosTheta)) (x) gauss(acos(cosTheta))
This tutorial requires FFT3 to be enabled.
␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m
Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
All rights reserved, please read http://roofit.sourceforge.net/license.txt
[#1] INFO:Caching -- Changing internal binning of variable 'psi' in FFT 'Mf' from 100 to 930 to improve the precision of the numerical FFT. This can be done manually by setting an additional binning named 'cache'.
[#1] INFO:Eval -- RooRealVar::setRange(psi) new range named 'refrange_fft_Mf' created with bounds [0,3.14159]
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_Int[psi]) using numeric integrator RooIntegrator1D to calculate Int(psi)
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55cedb253090 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[psi] for nset (psi) with code 0
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55cedb9d85a0 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[psi] for nset (psi) with code 0 from preexisting content.
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55cedb9d85a0 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[psi] for nset (psi) with code 0 from preexisting content.
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_Int[psi]) using numeric integrator RooIntegrator1D to calculate Int(psi)
[#1] INFO:Minization -- The following expressions have been identified as constant and will be precalculated and cached: (Tpsi)
**********
** 1 **SET PRINT 1
**********
**********
** 2 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 gbias 2.00000e-01 1.00000e-01 0.00000e+00 1.00000e+00
2 greso 3.00000e-01 9.00000e-02 1.00000e-01 1.00000e+00
**********
** 3 **SET ERR 0.5
**********
**********
** 4 **SET PRINT 1
**********
**********
** 5 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 6 **MIGRAD 1000 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_Int[psi]) using numeric integrator RooIntegrator1D to calculate Int(psi)
FCN=9480.16 FROM MIGRAD STATUS=INITIATE 8 CALLS 9 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 gbias 2.00000e-01 1.00000e-01 2.57889e-01 5.40962e+01
2 greso 3.00000e-01 9.00000e-02 2.46497e-01 5.76705e+00
ERR DEF= 0.5
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=9479.64 FROM MIGRAD STATUS=CONVERGED 32 CALLS 33 TOTAL
EDM=1.07647e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 gbias 1.92485e-01 7.44189e-03 1.26877e-03 1.36618e-02
2 greso 2.98582e-01 9.19693e-03 1.65656e-03 -8.25561e-03
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
5.539e-05 1.690e-07
1.690e-07 8.460e-05
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.00247 1.000 0.002
2 0.00247 0.002 1.000
**********
** 7 **SET ERR 0.5
**********
**********
** 8 **SET PRINT 1
**********
**********
** 9 **HESSE 1000
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=9479.64 FROM HESSE STATUS=OK 10 CALLS 43 TOTAL
EDM=1.07707e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 gbias 1.92485e-01 7.44188e-03 5.07510e-05 -6.62425e-01
2 greso 2.98582e-01 9.19691e-03 6.62625e-05 -5.92825e-01
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
5.539e-05 1.248e-07
1.248e-07 8.460e-05
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.00182 1.000 0.002
2 0.00182 0.002 1.000
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_Int[psi]) using numeric integrator RooIntegrator1D to calculate Int(psi)
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55cedbb12400 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[psi] for nset (psi) with code 0
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_Int[psi]) using numeric integrator RooIntegrator1D to calculate Int(psi)
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55cedbb12400 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[cpsi] for nset (cpsi) with code 0 from preexisting content.
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_CONV_Rpsi_CACHE_Obs[cpsi]_Int[cpsi]) using numeric integrator RooIntegrator1D to calculate Int(cpsi)
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55cedbb0fff0 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[cpsi] for nset (cpsi) with code 0 from preexisting content.
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_CONV_Rpsi_CACHE_Obs[cpsi]_Int[cpsi]) using numeric integrator RooIntegrator1D to calculate Int(cpsi)
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55cedbb0fff0 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[cpsi] for nset (cpsi) with code 0 from preexisting content.
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_CONV_Rpsi_CACHE_Obs[cpsi]_Int[cpsi]) using numeric integrator RooIntegrator1D to calculate Int(cpsi)
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
[#1] INFO:Minization -- The following expressions have been identified as constant and will be precalculated and cached: (psif)
**********
** 10 **SET PRINT 1
**********
**********
** 11 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 gbias 1.92485e-01 7.44188e-03 0.00000e+00 1.00000e+00
2 greso 2.98582e-01 9.19691e-03 1.00000e-01 1.00000e+00
**********
** 12 **SET ERR 0.5
**********
**********
** 13 **SET PRINT 1
**********
**********
** 14 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 15 **MIGRAD 1000 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_Int[psi]) using numeric integrator RooIntegrator1D to calculate Int(psi)
FCN=5178.91 FROM MIGRAD STATUS=INITIATE 4 CALLS 5 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 gbias 1.92485e-01 7.44188e-03 1.88791e-02 2.79436e+01
2 greso 2.98582e-01 9.19691e-03 2.46483e-02 -8.41273e+00
ERR DEF= 0.5
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=5178.63 FROM MIGRAD STATUS=CONVERGED 28 CALLS 29 TOTAL
EDM=3.37796e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 gbias 1.85814e-01 9.36461e-03 1.16493e-03 2.44691e-02
2 greso 3.02469e-01 1.02714e-02 1.32671e-03 1.52048e-03
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
8.771e-05 -2.174e-05
-2.174e-05 1.055e-04
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.22594 1.000 -0.226
2 0.22594 -0.226 1.000
**********
** 16 **SET ERR 0.5
**********
**********
** 17 **SET PRINT 1
**********
**********
** 18 **HESSE 1000
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=5178.63 FROM HESSE STATUS=OK 10 CALLS 39 TOTAL
EDM=3.36905e-07 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 gbias 1.85814e-01 9.36561e-03 2.32986e-04 -6.79459e-01
2 greso 3.02469e-01 1.02725e-02 5.30684e-05 -5.82446e-01
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 2 ERR DEF=0.5
8.773e-05 -2.179e-05
-2.179e-05 1.056e-04
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2
1 0.22639 1.000 -0.226
2 0.22639 -0.226 1.000
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_Int[psi]) using numeric integrator RooIntegrator1D to calculate Int(psi)
[#1] INFO:Caching -- RooAbsCachedPdf::getCache(Mf) creating new cache 0x55cedbb0fff0 with pdf Tpsi_CONV_Rpsi_CACHE_Obs[cpsi] for nset (cpsi) with code 0
[#1] INFO:NumericIntegration -- RooRealIntegral::init(Tpsi_CONV_Rpsi_CACHE_Obs[cpsi]_Int[cpsi]) using numeric integrator RooIntegrator1D to calculate Int(cpsi)
[#1] INFO:NumericIntegration -- RooRealIntegral::init(T_Int[cpsi]) using numeric integrator RooIntegrator1D to calculate Int(cpsi)



 Addition and convolution: convolution in cyclical angular observables theta
Addition and convolution: convolution in cyclical angular observables theta