StandardHypoTestDemo.C File Reference

Detailed Description

Standard tutorial macro for hypothesis test (for computing the discovery significance) using all RooStats hypotheiss tests calculators and test statistics.

Usage:

root>.L StandardHypoTestDemo.C
root> StandardHypoTestDemo("fileName","workspace name","S+B modelconfig name","B model name","data set
name",calculator type, test statistic type, number of toys)
 
 type = 0 Freq calculator
 type = 1 Hybrid calculator
 type = 2 Asymptotic calculator
 type = 3 Asymptotic calculator using nominal Asimov data sets (not using fitted parameter values but nominal ones)
 
testStatType = 0 LEP
             = 1 Tevatron
             = 2 Profile Likelihood
             = 3 Profile Likelihood one sided (i.e. = 0 if mu_hat < 0)

 
 
␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m 
                Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
                All rights reserved, please read http://roofit.sourceforge.net/license.txt
 
 
RooWorkspace(combined) combined contents
 
variables
---------
(Lumi,SigXsecOverSM,alpha_syst1,alpha_syst2,alpha_syst3,binWidth_obs_x_channel1_0,binWidth_obs_x_channel1_1,binWidth_obs_x_channel1_2,channelCat,gamma_stat_channel1_bin_0,gamma_stat_channel1_bin_1,nom_alpha_syst1,nom_alpha_syst2,nom_alpha_syst3,nom_gamma_stat_channel1_bin_0,nom_gamma_stat_channel1_bin_1,nominalLumi,obs_x_channel1,weightVar)
 
p.d.f.s
-------
RooGaussian::alpha_syst1Constraint[ x=alpha_syst1 mean=nom_alpha_syst1 sigma=1 ] = 1
RooGaussian::alpha_syst2Constraint[ x=alpha_syst2 mean=nom_alpha_syst2 sigma=1 ] = 1
RooGaussian::alpha_syst3Constraint[ x=alpha_syst3 mean=nom_alpha_syst3 sigma=1 ] = 1
RooRealSumPdf::channel1_model[ binWidth_obs_x_channel1_0 * L_x_signal_channel1_overallSyst_x_Exp + binWidth_obs_x_channel1_1 * L_x_background1_channel1_overallSyst_x_StatUncert + binWidth_obs_x_channel1_2 * L_x_background2_channel1_overallSyst_x_StatUncert ] = 220
RooPoisson::gamma_stat_channel1_bin_0_constraint[ x=nom_gamma_stat_channel1_bin_0 mean=gamma_stat_channel1_bin_0_poisMean ] = 0.019943
RooPoisson::gamma_stat_channel1_bin_1_constraint[ x=nom_gamma_stat_channel1_bin_1 mean=gamma_stat_channel1_bin_1_poisMean ] = 0.039861
RooGaussian::lumiConstraint[ x=Lumi mean=nominalLumi sigma=0.1 ] = 1
RooProdPdf::model_channel1[ lumiConstraint * alpha_syst1Constraint * alpha_syst2Constraint * alpha_syst3Constraint * gamma_stat_channel1_bin_0_constraint * gamma_stat_channel1_bin_1_constraint * channel1_model(obs_x_channel1) ] = 0.174888
RooSimultaneous::simPdf[ indexCat=channelCat channel1=model_channel1 ] = 0.174888
 
functions
--------
RooProduct::L_x_background1_channel1_overallSyst_x_StatUncert[ Lumi * background1_channel1_overallSyst_x_StatUncert ] = 0
RooProduct::L_x_background2_channel1_overallSyst_x_StatUncert[ Lumi * background2_channel1_overallSyst_x_StatUncert ] = 100
RooProduct::L_x_signal_channel1_overallSyst_x_Exp[ Lumi * signal_channel1_overallSyst_x_Exp ] = 10
RooStats::HistFactory::FlexibleInterpVar::background1_channel1_epsilon[ paramList=(alpha_syst2) ] = 1
RooHistFunc::background1_channel1_nominal[ depList=(obs_x_channel1) depList=(obs_x_channel1) ] = 0
RooProduct::background1_channel1_overallSyst_x_Exp[ background1_channel1_nominal * background1_channel1_epsilon ] = 0
RooProduct::background1_channel1_overallSyst_x_StatUncert[ mc_stat_channel1 * background1_channel1_overallSyst_x_Exp ] = 0
RooStats::HistFactory::FlexibleInterpVar::background2_channel1_epsilon[ paramList=(alpha_syst3) ] = 1
RooHistFunc::background2_channel1_nominal[ depList=(obs_x_channel1) depList=(obs_x_channel1) ] = 100
RooProduct::background2_channel1_overallSyst_x_Exp[ background2_channel1_nominal * background2_channel1_epsilon ] = 100
RooProduct::background2_channel1_overallSyst_x_StatUncert[ mc_stat_channel1 * background2_channel1_overallSyst_x_Exp ] = 100
RooProduct::gamma_stat_channel1_bin_0_poisMean[ gamma_stat_channel1_bin_0 * gamma_stat_channel1_bin_0_tau ] = 400
RooProduct::gamma_stat_channel1_bin_1_poisMean[ gamma_stat_channel1_bin_1 * gamma_stat_channel1_bin_1_tau ] = 100
ParamHistFunc::mc_stat_channel1[ ] = 1
RooStats::HistFactory::FlexibleInterpVar::signal_channel1_epsilon[ paramList=(alpha_syst1) ] = 1
RooHistFunc::signal_channel1_nominal[ depList=(obs_x_channel1) depList=(obs_x_channel1) ] = 10
RooProduct::signal_channel1_overallNorm_x_sigma_epsilon[ SigXsecOverSM * signal_channel1_epsilon ] = 1
RooProduct::signal_channel1_overallSyst_x_Exp[ signal_channel1_nominal * signal_channel1_overallNorm_x_sigma_epsilon ] = 10
 
datasets
--------
RooDataSet::asimovData(obs_x_channel1,weightVar,channelCat)
RooDataSet::obsData(channelCat,obs_x_channel1)
 
embedded datasets (in pdfs and functions)
-----------------------------------------
RooDataHist::signal_channel1nominalDHist(obs_x_channel1)
RooDataHist::background1_channel1nominalDHist(obs_x_channel1)
RooDataHist::background2_channel1nominalDHist(obs_x_channel1)
 
parameter snapshots
-------------------
NominalParamValues = (nom_alpha_syst2=0[C],nom_alpha_syst3=0[C],nom_gamma_stat_channel1_bin_0=400[C],nom_gamma_stat_channel1_bin_1=100[C],weightVar=0,obs_x_channel1=1.75,Lumi=1[C],nominalLumi=1[C],alpha_syst1=0[C],nom_alpha_syst1=0[C],alpha_syst2=0,alpha_syst3=0,gamma_stat_channel1_bin_0=1,gamma_stat_channel1_bin_1=1,SigXsecOverSM=1,binWidth_obs_x_channel1_0=2[C],binWidth_obs_x_channel1_1=2[C],binWidth_obs_x_channel1_2=2[C])
 
named sets
----------
ModelConfig_GlobalObservables:(nom_alpha_syst2,nom_alpha_syst3,nom_gamma_stat_channel1_bin_0,nom_gamma_stat_channel1_bin_1)
ModelConfig_NuisParams:(alpha_syst2,alpha_syst3,gamma_stat_channel1_bin_0,gamma_stat_channel1_bin_1)
ModelConfig_Observables:(obs_x_channel1,weightVar,channelCat)
ModelConfig_POI:(SigXsecOverSM)
globalObservables:(nom_alpha_syst2,nom_alpha_syst3,nom_gamma_stat_channel1_bin_0,nom_gamma_stat_channel1_bin_1)
observables:(obs_x_channel1,weightVar,channelCat)
 
generic objects
---------------
RooStats::ModelConfig::ModelConfig
 
 
=== Using the following for ModelConfigB_only ===
Observables:             RooArgSet:: = (obs_x_channel1,weightVar,channelCat)
Parameters of Interest:  RooArgSet:: = (SigXsecOverSM)
Nuisance Parameters:     RooArgSet:: = (alpha_syst2,alpha_syst3,gamma_stat_channel1_bin_0,gamma_stat_channel1_bin_1)
Global Observables:      RooArgSet:: = (nom_alpha_syst2,nom_alpha_syst3,nom_gamma_stat_channel1_bin_0,nom_gamma_stat_channel1_bin_1)
PDF:                     RooSimultaneous::simPdf[ indexCat=channelCat channel1=model_channel1 ] = 0.174888
Snapshot:                
  1) 0x55d79c32deb0 RooRealVar:: SigXsecOverSM = 0  L(0 - 3)  "SigXsecOverSM"
 
 
=== Using the following for ModelConfig ===
Observables:             RooArgSet:: = (obs_x_channel1,weightVar,channelCat)
Parameters of Interest:  RooArgSet:: = (SigXsecOverSM)
Nuisance Parameters:     RooArgSet:: = (alpha_syst2,alpha_syst3,gamma_stat_channel1_bin_0,gamma_stat_channel1_bin_1)
Global Observables:      RooArgSet:: = (nom_alpha_syst2,nom_alpha_syst3,nom_gamma_stat_channel1_bin_0,nom_gamma_stat_channel1_bin_1)
PDF:                     RooSimultaneous::simPdf[ indexCat=channelCat channel1=model_channel1 ] = 0.174888
Snapshot:                
  1) 0x55d79c330000 RooRealVar:: SigXsecOverSM = 1  L(0 - 3)  "SigXsecOverSM"
 
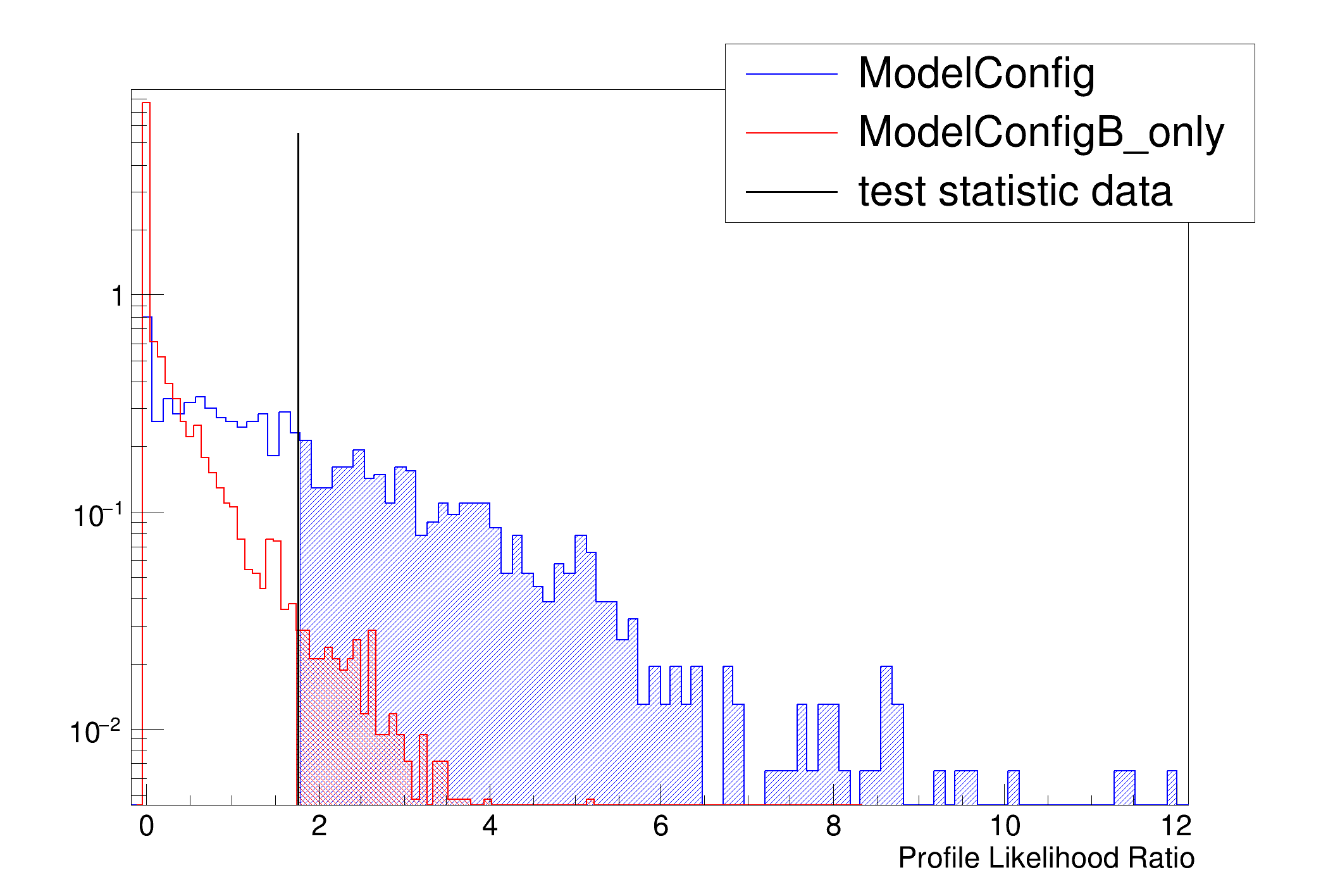
[#0] PROGRESS:Generation -- Test Statistic on data: 1.77404
[#1] INFO:InputArguments -- Profiling conditional MLEs for Null.
[#1] INFO:InputArguments -- Using a ToyMCSampler. Now configuring for Null.
[#0] PROGRESS:Generation -- generated toys: 500 / 5000
[#0] PROGRESS:Generation -- generated toys: 1000 / 5000
[#0] PROGRESS:Generation -- generated toys: 1500 / 5000
[#0] PROGRESS:Generation -- generated toys: 2000 / 5000
[#0] PROGRESS:Generation -- generated toys: 2500 / 5000
[#0] PROGRESS:Generation -- generated toys: 3000 / 5000
[#0] PROGRESS:Generation -- generated toys: 3500 / 5000
[#0] PROGRESS:Generation -- generated toys: 4000 / 5000
[#0] PROGRESS:Generation -- generated toys: 4500 / 5000
[#1] INFO:InputArguments -- Profiling conditional MLEs for Alt.
[#1] INFO:InputArguments -- Using a ToyMCSampler. Now configuring for Alt.
[#0] PROGRESS:Generation -- generated toys: 500 / 1250
[#0] PROGRESS:Generation -- generated toys: 1000 / 1250
 
Results HypoTestCalculator_result: 
 - Null p-value = 0.0304 +/- 0.002428
 - Significance = 1.87495 +/- 0.0352942 sigma
 - Number of Alt toys: 1250
 - Number of Null toys: 5000
 - Test statistic evaluated on data: 1.77404
 - CL_b: 0.0304 +/- 0.002428
 - CL_s+b: 0.4328 +/- 0.0140138
 - CL_s: 14.2368 +/- 1.22696
 Expected p -value and significance at -2 sigma = 0.839 significance -0.990356 sigma 
 Expected p -value and significance at -1 sigma = 0.2238 significance 0.759422 sigma 
 Expected p -value and significance at 0 sigma = 0.0434 significance 1.71252 sigma 
 Expected p -value and significance at 1 sigma = 0.0028 significance 2.77033 sigma 
 Expected p -value and significance at 2 sigma = 0.0002 significance 3.54008 sigma 

 
#include "TFile.h"
#include "RooWorkspace.h"
#include "RooAbsPdf.h"
#include "RooRealVar.h"
#include "RooDataSet.h"
#include "RooStats/ModelConfig.h"
#include "RooRandom.h"
#include "TGraphErrors.h"
#include "TGraphAsymmErrors.h"
#include "TCanvas.h"
#include "TLine.h"
#include "TSystem.h"
#include "TROOT.h"
 
#include "RooStats/AsymptoticCalculator.h"
#include "RooStats/HybridCalculator.h"
#include "RooStats/FrequentistCalculator.h"
#include "RooStats/ToyMCSampler.h"
#include "RooStats/HypoTestPlot.h"
 
#include "RooStats/NumEventsTestStat.h"
#include "RooStats/ProfileLikelihoodTestStat.h"
#include "RooStats/SimpleLikelihoodRatioTestStat.h"
#include "RooStats/RatioOfProfiledLikelihoodsTestStat.h"
#include "RooStats/MaxLikelihoodEstimateTestStat.h"
 
#include "RooStats/HypoTestInverter.h"
#include "RooStats/HypoTestInverterResult.h"
#include "RooStats/HypoTestInverterPlot.h"
 
#include <cassert>
 
using namespace RooFit;
using namespace RooStats;
 
struct HypoTestOptions {
 
   bool noSystematics = false; // force all systematics to be off (i.e. set all nuisance parameters as constat
   double nToysRatio = 4;      // ratio Ntoys Null/ntoys ALT
   double poiValue = -1;       // change poi snapshot value for S+B model (needed for expected p0 values)
   int printLevel = 0;
   bool generateBinned = false;       // for binned generation
   bool useProof = false;             // use Proof
   bool enableDetailedOutput = false; // for detailed output
};
 
HypoTestOptions optHT;
 
void StandardHypoTestDemo(const char *infile = "", const char *workspaceName = "combined",
                          const char *modelSBName = "ModelConfig", const char *modelBName = "",
                          const char *dataName = "obsData", int calcType = 0, /* 0 freq 1 hybrid, 2 asymptotic */
                          int testStatType = 3, /* 0 LEP, 1 TeV, 2 LHC, 3 LHC - one sided*/
                          int ntoys = 5000, bool useNC = false, const char *nuisPriorName = 0)
{
 
   bool noSystematics = optHT.noSystematics;
   double nToysRatio = optHT.nToysRatio; // ratio Ntoys Null/ntoys ALT
   double poiValue = optHT.poiValue;     // change poi snapshot value for S+B model (needed for expected p0 values)
   int printLevel = optHT.printLevel;
   bool generateBinned = optHT.generateBinned; // for binned generation
   bool useProof = optHT.useProof;             // use Proof
   bool enableDetOutput = optHT.enableDetailedOutput;
 
   // Other Parameter to pass in tutorial
   // apart from standard for filename, ws, modelconfig and data
 
   // type = 0 Freq calculator
   // type = 1 Hybrid calculator
   // type = 2 Asymptotic calculator
 
   // testStatType = 0 LEP
   // = 1 Tevatron
   // = 2 Profile Likelihood
   // = 3 Profile Likelihood one sided (i.e. = 0 if mu < mu_hat)
 
   // ntoys:         number of toys to use
 
   // useNumberCounting:  set to true when using number counting events
 
   // nuisPriorName:   name of prior for the nuisance. This is often expressed as constraint term in the global model
   // It is needed only when using the HybridCalculator (type=1)
   // If not given by default the prior pdf from ModelConfig is used.
 
   // extra options are available as global parameters of the macro. They major ones are:
 
   // generateBinned       generate binned data sets for toys (default is false) - be careful not to activate with
   // a too large (>=3) number of observables
   // nToyRatio            ratio of S+B/B toys (default is 2)
   // printLevel
 
   // disable - can cause some problems
   // ToyMCSampler::SetAlwaysUseMultiGen(true);
 
   SimpleLikelihoodRatioTestStat::SetAlwaysReuseNLL(true);
   ProfileLikelihoodTestStat::SetAlwaysReuseNLL(true);
   RatioOfProfiledLikelihoodsTestStat::SetAlwaysReuseNLL(true);
 
   // RooRandom::randomGenerator()->SetSeed(0);
 
   // to change minimizers
   // ~~~{.bash}
   // ROOT::Math::MinimizerOptions::SetDefaultStrategy(0);
   // ROOT::Math::MinimizerOptions::SetDefaultMinimizer("Minuit2");
   // ROOT::Math::MinimizerOptions::SetDefaultTolerance(1);
   // ~~~
 
   // -------------------------------------------------------
   // First part is just to access a user-defined file
   // or create the standard example file if it doesn't exist
   const char *filename = "";
   if (!strcmp(infile, "")) {
      filename = "results/example_combined_GaussExample_model.root";
      bool fileExist = !gSystem->AccessPathName(filename); // note opposite return code
      // if file does not exists generate with histfactory
      if (!fileExist) {
#ifdef _WIN32
         cout << "HistFactory file cannot be generated on Windows - exit" << endl;
         return;
#endif
         // Normally this would be run on the command line
         cout << "will run standard hist2workspace example" << endl;
         gROOT->ProcessLine(".! prepareHistFactory .");
         gROOT->ProcessLine(".! hist2workspace config/example.xml");
         cout << "\n\n---------------------" << endl;
         cout << "Done creating example input" << endl;
         cout << "---------------------\n\n" << endl;
      }
 
   } else
      filename = infile;
 
   // Try to open the file
   TFile *file = TFile::Open(filename);
 
   // if input file was specified byt not found, quit
   if (!file) {
      cout << "StandardRooStatsDemoMacro: Input file " << filename << " is not found" << endl;
      return;
   }
 
   // -------------------------------------------------------
   // Tutorial starts here
   // -------------------------------------------------------
 
   // get the workspace out of the file
   RooWorkspace *w = (RooWorkspace *)file->Get(workspaceName);
   if (!w) {
      cout << "workspace not found" << endl;
      return;
   }
   w->Print();
 
   // get the modelConfig out of the file
   ModelConfig *sbModel = (ModelConfig *)w->obj(modelSBName);
 
   // get the modelConfig out of the file
   RooAbsData *data = w->data(dataName);
 
   // make sure ingredients are found
   if (!data || !sbModel) {
      w->Print();
      cout << "data or ModelConfig was not found" << endl;
      return;
   }
   // make b model
   ModelConfig *bModel = (ModelConfig *)w->obj(modelBName);
 
   // case of no systematics
   // remove nuisance parameters from model
   if (noSystematics) {
      const RooArgSet *nuisPar = sbModel->GetNuisanceParameters();
      if (nuisPar && nuisPar->getSize() > 0) {
         std::cout << "StandardHypoTestInvDemo"
                   << "  -  Switch off all systematics by setting them constant to their initial values" << std::endl;
         RooStats::SetAllConstant(*nuisPar);
      }
      if (bModel) {
         const RooArgSet *bnuisPar = bModel->GetNuisanceParameters();
         if (bnuisPar)
            RooStats::SetAllConstant(*bnuisPar);
      }
   }
 
   if (!bModel) {
      Info("StandardHypoTestInvDemo", "The background model %s does not exist", modelBName);
      Info("StandardHypoTestInvDemo", "Copy it from ModelConfig %s and set POI to zero", modelSBName);
      bModel = (ModelConfig *)sbModel->Clone();
      bModel->SetName(TString(modelSBName) + TString("B_only"));
      RooRealVar *var = dynamic_cast<RooRealVar *>(bModel->GetParametersOfInterest()->first());
      if (!var)
         return;
      double oldval = var->getVal();
      var->setVal(0);
      // bModel->SetSnapshot( RooArgSet(*var, *w->var("lumi"))  );
      bModel->SetSnapshot(RooArgSet(*var));
      var->setVal(oldval);
   }
 
   if (!sbModel->GetSnapshot() || poiValue > 0) {
      Info("StandardHypoTestDemo", "Model %s has no snapshot  - make one using model poi", modelSBName);
      RooRealVar *var = dynamic_cast<RooRealVar *>(sbModel->GetParametersOfInterest()->first());
      if (!var)
         return;
      double oldval = var->getVal();
      if (poiValue > 0)
         var->setVal(poiValue);
      // sbModel->SetSnapshot( RooArgSet(*var, *w->var("lumi") ) );
      sbModel->SetSnapshot(RooArgSet(*var));
      if (poiValue > 0)
         var->setVal(oldval);
      // sbModel->SetSnapshot( *sbModel->GetParametersOfInterest() );
   }
 
   // part 1, hypothesis testing
   SimpleLikelihoodRatioTestStat *slrts = new SimpleLikelihoodRatioTestStat(*bModel->GetPdf(), *sbModel->GetPdf());
   // null parameters must includes snapshot of poi plus the nuisance values
   RooArgSet nullParams(*bModel->GetSnapshot());
   if (bModel->GetNuisanceParameters())
      nullParams.add(*bModel->GetNuisanceParameters());
 
   slrts->SetNullParameters(nullParams);
   RooArgSet altParams(*sbModel->GetSnapshot());
   if (sbModel->GetNuisanceParameters())
      altParams.add(*sbModel->GetNuisanceParameters());
   slrts->SetAltParameters(altParams);
 
   ProfileLikelihoodTestStat *profll = new ProfileLikelihoodTestStat(*bModel->GetPdf());
 
   RatioOfProfiledLikelihoodsTestStat *ropl =
      new RatioOfProfiledLikelihoodsTestStat(*bModel->GetPdf(), *sbModel->GetPdf(), sbModel->GetSnapshot());
   ropl->SetSubtractMLE(false);
 
   if (testStatType == 3)
      profll->SetOneSidedDiscovery(1);
   profll->SetPrintLevel(printLevel);
 
   if (enableDetOutput) {
      slrts->EnableDetailedOutput();
      profll->EnableDetailedOutput();
      ropl->EnableDetailedOutput();
   }
 
   /* profll.SetReuseNLL(mOptimize);*/
   /* slrts.SetReuseNLL(mOptimize);*/
   /* ropl.SetReuseNLL(mOptimize);*/
 
   AsymptoticCalculator::SetPrintLevel(printLevel);
 
   HypoTestCalculatorGeneric *hypoCalc = 0;
   // note here Null is B and Alt is S+B
   if (calcType == 0)
      hypoCalc = new FrequentistCalculator(*data, *sbModel, *bModel);
   else if (calcType == 1)
      hypoCalc = new HybridCalculator(*data, *sbModel, *bModel);
   else if (calcType == 2)
      hypoCalc = new AsymptoticCalculator(*data, *sbModel, *bModel);
 
   if (calcType == 0) {
      ((FrequentistCalculator *)hypoCalc)->SetToys(ntoys, ntoys / nToysRatio);
      if (enableDetOutput)
         ((FrequentistCalculator *)hypoCalc)->StoreFitInfo(true);
   }
   if (calcType == 1) {
      ((HybridCalculator *)hypoCalc)->SetToys(ntoys, ntoys / nToysRatio);
      // n. a. yetif (enableDetOutput) ((HybridCalculator*) hypoCalc)->StoreFitInfo(true);
   }
   if (calcType == 2) {
      if (testStatType == 3)
         ((AsymptoticCalculator *)hypoCalc)->SetOneSidedDiscovery(true);
      if (testStatType != 2 && testStatType != 3)
         Warning("StandardHypoTestDemo",
                 "Only the PL test statistic can be used with AsymptoticCalculator - use by default a two-sided PL");
   }
 
   // check for nuisance prior pdf in case of nuisance parameters
   if (calcType == 1 && (bModel->GetNuisanceParameters() || sbModel->GetNuisanceParameters())) {
      RooAbsPdf *nuisPdf = 0;
      if (nuisPriorName)
         nuisPdf = w->pdf(nuisPriorName);
      // use prior defined first in bModel (then in SbModel)
      if (!nuisPdf) {
         Info("StandardHypoTestDemo",
              "No nuisance pdf given for the HybridCalculator - try to deduce  pdf from the   model");
         if (bModel->GetPdf() && bModel->GetObservables())
            nuisPdf = RooStats::MakeNuisancePdf(*bModel, "nuisancePdf_bmodel");
         else
            nuisPdf = RooStats::MakeNuisancePdf(*sbModel, "nuisancePdf_sbmodel");
      }
      if (!nuisPdf) {
         if (bModel->GetPriorPdf()) {
            nuisPdf = bModel->GetPriorPdf();
            Info("StandardHypoTestDemo",
                 "No nuisance pdf given - try to use %s that is defined as a prior pdf in the B model",
                 nuisPdf->GetName());
         } else {
            Error("StandardHypoTestDemo", "Cannot run Hybrid calculator because no prior on the nuisance parameter is "
                                          "specified or can be derived");
            return;
         }
      }
      assert(nuisPdf);
      Info("StandardHypoTestDemo", "Using as nuisance Pdf ... ");
      nuisPdf->Print();
 
      const RooArgSet *nuisParams =
         (bModel->GetNuisanceParameters()) ? bModel->GetNuisanceParameters() : sbModel->GetNuisanceParameters();
      RooArgSet *np = nuisPdf->getObservables(*nuisParams);
      if (np->getSize() == 0) {
         Warning("StandardHypoTestDemo",
                 "Prior nuisance does not depend on nuisance parameters. They will be smeared in their full range");
      }
      delete np;
 
      ((HybridCalculator *)hypoCalc)->ForcePriorNuisanceAlt(*nuisPdf);
      ((HybridCalculator *)hypoCalc)->ForcePriorNuisanceNull(*nuisPdf);
   }
 
   /* hypoCalc->ForcePriorNuisanceAlt(*sbModel->GetPriorPdf());*/
   /* hypoCalc->ForcePriorNuisanceNull(*bModel->GetPriorPdf());*/
 
   ToyMCSampler *sampler = (ToyMCSampler *)hypoCalc->GetTestStatSampler();
 
   if (sampler && (calcType == 0 || calcType == 1)) {
 
      // look if pdf is number counting or extended
      if (sbModel->GetPdf()->canBeExtended()) {
         if (useNC)
            Warning("StandardHypoTestDemo", "Pdf is extended: but number counting flag is set: ignore it ");
      } else {
         // for not extended pdf
         if (!useNC) {
            int nEvents = data->numEntries();
            Info("StandardHypoTestDemo",
                 "Pdf is not extended: number of events to generate taken  from observed data set is %d", nEvents);
            sampler->SetNEventsPerToy(nEvents);
         } else {
            Info("StandardHypoTestDemo", "using a number counting pdf");
            sampler->SetNEventsPerToy(1);
         }
      }
 
      if (data->isWeighted() && !generateBinned) {
         Info("StandardHypoTestDemo", "Data set is weighted, nentries = %d and sum of weights = %8.1f but toy "
                                      "generation is unbinned - it would be faster to set generateBinned to true\n",
              data->numEntries(), data->sumEntries());
      }
      if (generateBinned)
         sampler->SetGenerateBinned(generateBinned);
 
      // use PROOF
      if (useProof) {
         ProofConfig pc(*w, 0, "", kFALSE);
         sampler->SetProofConfig(&pc); // enable proof
      }
 
      // set the test statistic
      if (testStatType == 0)
         sampler->SetTestStatistic(slrts);
      if (testStatType == 1)
         sampler->SetTestStatistic(ropl);
      if (testStatType == 2 || testStatType == 3)
         sampler->SetTestStatistic(profll);
   }
 
   HypoTestResult *htr = hypoCalc->GetHypoTest();
   htr->SetPValueIsRightTail(true);
   htr->SetBackgroundAsAlt(false);
   htr->Print(); // how to get meaningful CLs at this point?
 
   delete sampler;
   delete slrts;
   delete ropl;
   delete profll;
 
   if (calcType != 2) {
      HypoTestPlot *plot = new HypoTestPlot(*htr, 100);
      plot->SetLogYaxis(true);
      plot->Draw();
   } else {
      std::cout << "Asymptotic results " << std::endl;
   }
 
   // look at expected significances
   // found median of S+B distribution
   if (calcType != 2) {
 
      SamplingDistribution *altDist = htr->GetAltDistribution();
      HypoTestResult htExp("Expected Result");
      htExp.Append(htr);
      // find quantiles in alt (S+B) distribution
      double p[5];
      double q[5];
      for (int i = 0; i < 5; ++i) {
         double sig = -2 + i;
         p[i] = ROOT::Math::normal_cdf(sig, 1);
      }
      std::vector<double> values = altDist->GetSamplingDistribution();
      TMath::Quantiles(values.size(), 5, &values[0], q, p, false);
 
      for (int i = 0; i < 5; ++i) {
         htExp.SetTestStatisticData(q[i]);
         double sig = -2 + i;
         std::cout << " Expected p -value and significance at " << sig << " sigma = " << htExp.NullPValue()
                   << " significance " << htExp.Significance() << " sigma " << std::endl;
      }
   } else {
      // case of asymptotic calculator
      for (int i = 0; i < 5; ++i) {
         double sig = -2 + i;
         // sigma is inverted here
         double pval = AsymptoticCalculator::GetExpectedPValues(htr->NullPValue(), htr->AlternatePValue(), -sig, false);
         std::cout << " Expected p -value and significance at " << sig << " sigma = " << pval << " significance "
                   << ROOT::Math::normal_quantile_c(pval, 1) << " sigma " << std::endl;
      }
   }
 
   // write result in a file in case of toys
   bool writeResult = (calcType != 2);
 
   if (enableDetOutput) {
      writeResult = true;
      Info("StandardHypoTestDemo", "Detailed output will be written in output result file");
   }
 
   if (htr != NULL && writeResult) {
 
      // write to a file the results
      const char *calcTypeName = (calcType == 0) ? "Freq" : (calcType == 1) ? "Hybr" : "Asym";
      TString resultFileName = TString::Format("%s_HypoTest_ts%d_", calcTypeName, testStatType);
      // strip the / from the filename
 
      TString name = infile;
      name.Replace(0, name.Last('/') + 1, "");
      resultFileName += name;
 
      TFile *fileOut = new TFile(resultFileName, "RECREATE");
      htr->Write();
      Info("StandardHypoTestDemo", "HypoTestResult has been written in the file %s", resultFileName.Data());
 
      fileOut->Close();
   }
}

Author

Lorenzo Moneta

Definition in file StandardHypoTestDemo.C.