StandardBayesianMCMCDemo.C File Reference

Detailed Description

Standard demo of the Bayesian MCMC calculator

This is a standard demo that can be used with any ROOT file prepared in the standard way. You specify:

• name for input ROOT file
• name of workspace inside ROOT file that holds model and data
• name of ModelConfig that specifies details for calculator tools
• name of dataset

With default parameters the macro will attempt to run the standard hist2workspace example and read the ROOT file that it produces.

The actual heart of the demo is only about 10 lines long.

The MCMCCalculator is a Bayesian tool that uses the Metropolis-Hastings algorithm to efficiently integrate in many dimensions. It is not as accurate as the BayesianCalculator for simple problems, but it scales to much more complicated cases.

 
 
␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m 
                Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
                All rights reserved, please read http://roofit.sourceforge.net/license.txt
 
[#1] INFO:Minization -- p.d.f. provides expected number of events, including extended term in likelihood.
[#1] INFO:Minization -- createNLL: caching constraint set under name CONSTR_OF_PDF_simPdf_FOR_OBS_channelCat:obs_x_channel1 with 6 entries
[#1] INFO:Minization --  Including the following contraint terms in minimization: (lumiConstraint,alpha_syst1Constraint,alpha_syst2Constraint,alpha_syst3Constraint,gamma_stat_channel1_bin_0_constraint,gamma_stat_channel1_bin_1_constraint)
[#1] INFO:Minization -- The following global observables have been defined: (nom_alpha_syst2,nom_alpha_syst3,nom_gamma_stat_channel1_bin_0,nom_gamma_stat_channel1_bin_1)
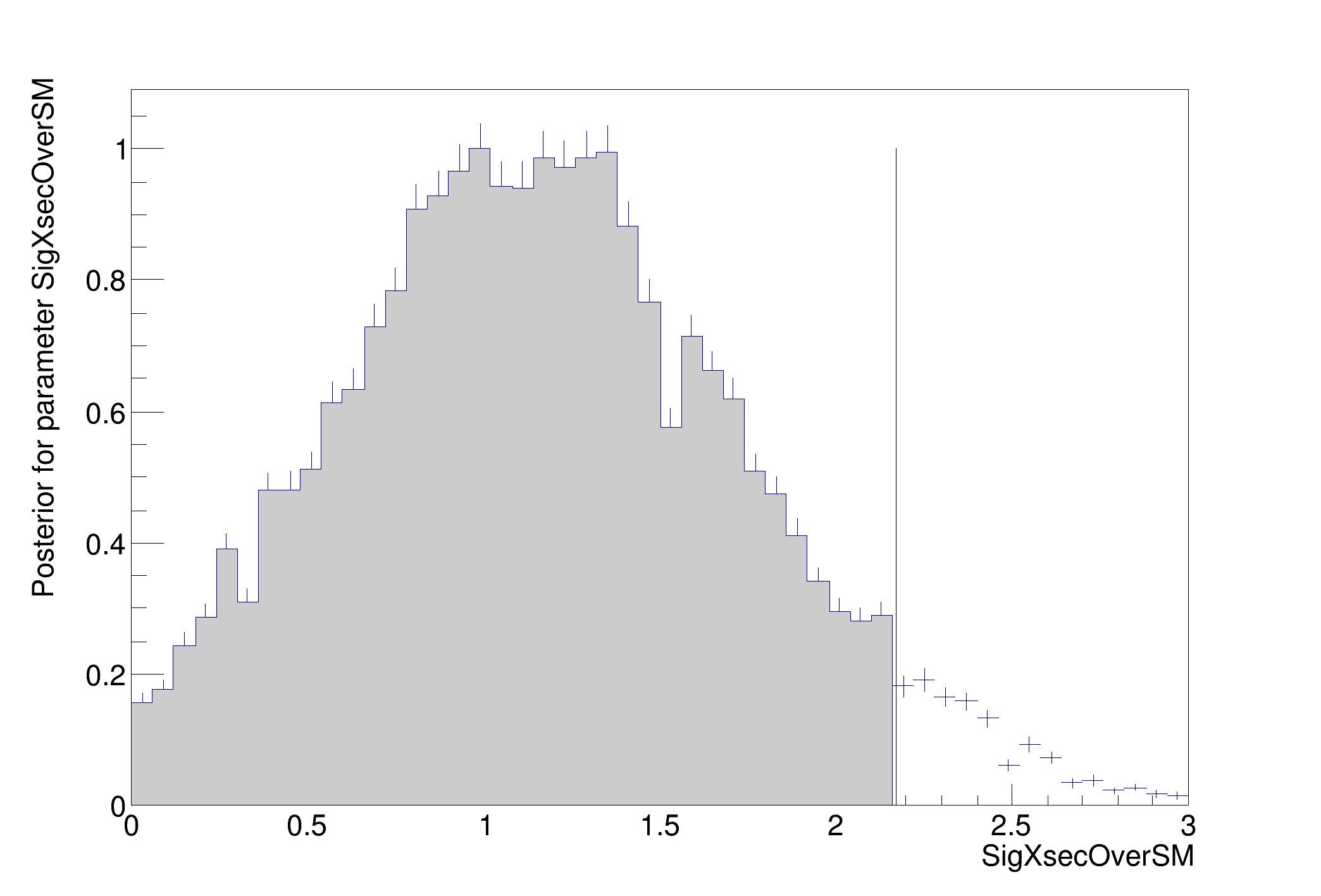
Metropolis-Hastings progress: ....................................................................................................
[#1] INFO:Eval -- Proposal acceptance rate: 27.377%
[#1] INFO:Eval -- Number of steps in chain: 27377
 
>>>> RESULT : 95% interval on SigXsecOverSM is : [0, 2.17276] 

 
#include "TFile.h"
#include "TROOT.h"
#include "TCanvas.h"
#include "TMath.h"
#include "TSystem.h"
#include "RooWorkspace.h"
#include "RooAbsData.h"
 
#include "RooStats/ModelConfig.h"
#include "RooStats/MCMCCalculator.h"
#include "RooStats/MCMCInterval.h"
#include "RooStats/MCMCIntervalPlot.h"
#include "RooStats/SequentialProposal.h"
#include "RooStats/ProposalHelper.h"
#include "RooStats/ProposalHelper.h"
#include "RooFitResult.h"
 
 
using namespace RooFit;
using namespace RooStats;
 
struct BayesianMCMCOptions {
 
   double confLevel = 0.95;
   int intervalType = 2;          // type of interval (0 is shortest, 1 central, 2 upper limit)
   double   maxPOI = -999;        // force different values of POI for doing the scan (default is given value)
   double   minPOI = -999;
   int numIters = 100000;         // number of iterations
   int numBurnInSteps = 100;      // number of burn in steps to be ignored
};
 
BayesianMCMCOptions optMCMC;
 
void StandardBayesianMCMCDemo(const char* infile = "",
                              const char* workspaceName = "combined",
                              const char* modelConfigName = "ModelConfig",
                              const char* dataName = "obsData"){
 
   // -------------------------------------------------------
   // First part is just to access a user-defined file
   // or create the standard example file if it doesn't exist
 
 
 
      const char* filename = "";
      if (!strcmp(infile,"")) {
         filename = "results/example_combined_GaussExample_model.root";
         bool fileExist = !gSystem->AccessPathName(filename); // note opposite return code
         // if file does not exists generate with histfactory
         if (!fileExist) {
#ifdef _WIN32
            cout << "HistFactory file cannot be generated on Windows - exit" << endl;
            return;
#endif
            // Normally this would be run on the command line
            cout <<"will run standard hist2workspace example"<<endl;
            gROOT->ProcessLine(".! prepareHistFactory .");
            gROOT->ProcessLine(".! hist2workspace config/example.xml");
            cout <<"\n\n---------------------"<<endl;
            cout <<"Done creating example input"<<endl;
            cout <<"---------------------\n\n"<<endl;
         }
 
      }
      else
         filename = infile;
 
      // Try to open the file
      TFile *file = TFile::Open(filename);
 
      // if input file was specified byt not found, quit
      if(!file ){
         cout <<"StandardRooStatsDemoMacro: Input file " << filename << " is not found" << endl;
         return;
      }
 
 
 
   // -------------------------------------------------------
   // Tutorial starts here
   // -------------------------------------------------------
 
   // get the workspace out of the file
   RooWorkspace* w = (RooWorkspace*) file->Get(workspaceName);
   if(!w){
      cout <<"workspace not found" << endl;
      return;
   }
 
   // get the modelConfig out of the file
   ModelConfig* mc = (ModelConfig*) w->obj(modelConfigName);
 
   // get the modelConfig out of the file
   RooAbsData* data = w->data(dataName);
 
   // make sure ingredients are found
   if(!data || !mc){
      w->Print();
      cout << "data or ModelConfig was not found" <<endl;
      return;
   }
 
   // Want an efficient proposal function
   // default is uniform.
 
   /*
   // this one is based on the covariance matrix of fit
   RooFitResult* fit = mc->GetPdf()->fitTo(*data,Save());
   ProposalHelper ph;
   ph.SetVariables((RooArgSet&)fit->floatParsFinal());
   ph.SetCovMatrix(fit->covarianceMatrix());
   ph.SetUpdateProposalParameters(kTRUE); // auto-create mean vars and add mappings
   ph.SetCacheSize(100);
   ProposalFunction* pf = ph.GetProposalFunction();
   */
 
   // this proposal function seems fairly robust
   SequentialProposal sp(0.1);
   // -------------------------------------------------------
   // create and use the MCMCCalculator
   // to find and plot the 95% credible interval
   // on the parameter of interest as specified
   // in the model config
   MCMCCalculator mcmc(*data,*mc);
   mcmc.SetConfidenceLevel(optMCMC.confLevel); // 95% interval
   //  mcmc.SetProposalFunction(*pf);
   mcmc.SetProposalFunction(sp);
   mcmc.SetNumIters(optMCMC.numIters);         // Metropolis-Hastings algorithm iterations
   mcmc.SetNumBurnInSteps(optMCMC.numBurnInSteps);       // first N steps to be ignored as burn-in
 
   // default is the shortest interval.
   if (optMCMC.intervalType == 0)  mcmc.SetIntervalType(MCMCInterval::kShortest); // for shortest interval (not really needed)
   if (optMCMC.intervalType == 1)  mcmc.SetLeftSideTailFraction(0.5); // for central interval
   if (optMCMC.intervalType == 2)  mcmc.SetLeftSideTailFraction(0.); // for upper limit
 
   RooRealVar* firstPOI = (RooRealVar*) mc->GetParametersOfInterest()->first();
   if (optMCMC.minPOI != -999)
      firstPOI->setMin(optMCMC.minPOI);
   if (optMCMC.maxPOI != -999)
      firstPOI->setMax(optMCMC.maxPOI);
 
   MCMCInterval* interval = mcmc.GetInterval();
 
   // make a plot
   //TCanvas* c1 =
   auto c1 = new TCanvas("IntervalPlot");
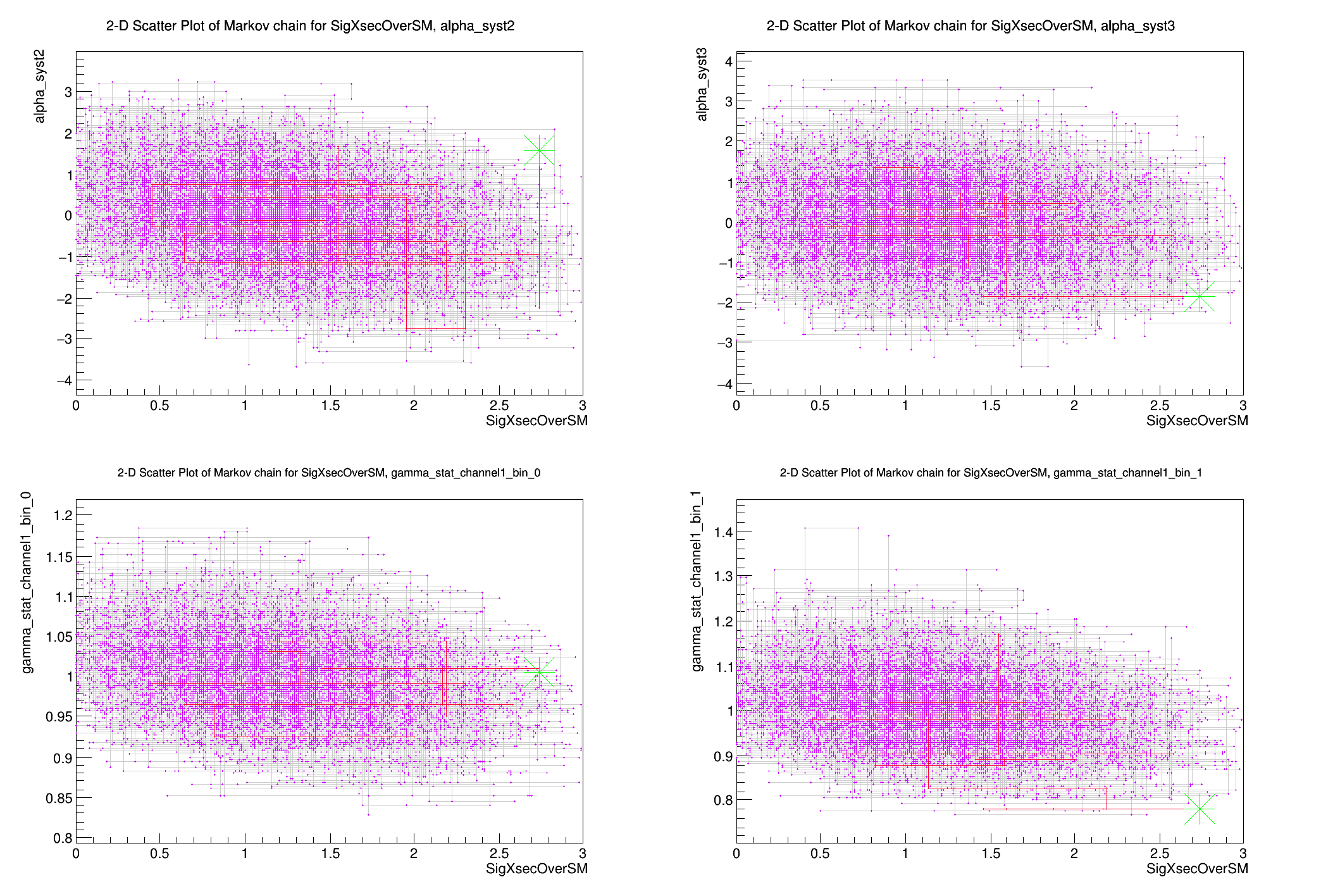
   MCMCIntervalPlot plot(*interval);
   plot.Draw();
 
   TCanvas* c2 = new TCanvas("extraPlots");
   const RooArgSet* list = mc->GetNuisanceParameters();
   if(list->getSize()>1){
      double n = list->getSize();
      int ny = TMath::CeilNint( sqrt(n) );
      int nx = TMath::CeilNint(double(n)/ny);
      c2->Divide( nx,ny);
   }
 
   // draw a scatter plot of chain results for poi vs each nuisance parameters
   TIterator* it = mc->GetNuisanceParameters()->createIterator();
   RooRealVar* nuis = NULL;
   int iPad=1; // iPad, that's funny
   while( (nuis = (RooRealVar*) it->Next() )){
      c2->cd(iPad++);
      plot.DrawChainScatter(*firstPOI,*nuis);
   }
 
   // print out the interval on the first Parameter of Interest
      cout << "\n>>>> RESULT : " << optMCMC.confLevel*100 <<  "% interval on " <<firstPOI->GetName()<<" is : ["<<
      interval->LowerLimit(*firstPOI) << ", "<<
      interval->UpperLimit(*firstPOI) <<"] "<<endl;
 
 
      gPad = c1;
}

Author

Kyle Cranmer

Definition in file StandardBayesianMCMCDemo.C.