This tutorial produces an N-dimensional multivariate Gaussian with a non-trivial covariance matrix. By default N=4 (called "dim").
A subset of these are considered parameters of interest. This problem is tractable analytically.
We use this mainly as a test of Markov Chain Monte Carlo and we compare the result to the profile likelihood ratio.
We use the proposal helper to create a customized proposal function for this problem.
For N=4 and 2 parameters of interest it takes about 10-20 seconds and the acceptance rate is 37%
␛[1mRooFit v3.60 -- Developed by Wouter Verkerke and David Kirkby␛[0m
Copyright (C) 2000-2013 NIKHEF, University of California & Stanford University
All rights reserved, please read http://roofit.sourceforge.net/license.txt
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
**********
** 1 **SET PRINT 1
**********
**********
** 2 **SET NOGRAD
**********
PARAMETER DEFINITIONS:
NO. NAME VALUE STEP SIZE LIMITS
1 mu_x0 0.00000e+00 4.00000e-01 -2.00000e+00 2.00000e+00
2 mu_x1 0.00000e+00 4.00000e-01 -2.00000e+00 2.00000e+00
3 mu_x2 0.00000e+00 4.00000e-01 -2.00000e+00 2.00000e+00
4 mu_x3 0.00000e+00 4.00000e-01 -2.00000e+00 2.00000e+00
**********
** 3 **SET ERR 0.5
**********
**********
** 4 **SET PRINT 1
**********
**********
** 5 **SET STR 1
**********
NOW USING STRATEGY 1: TRY TO BALANCE SPEED AGAINST RELIABILITY
**********
** 6 **MIGRAD 2000 1
**********
FIRST CALL TO USER FUNCTION AT NEW START POINT, WITH IFLAG=4.
START MIGRAD MINIMIZATION. STRATEGY 1. CONVERGENCE WHEN EDM .LT. 1.00e-03
FCN=707.822 FROM MIGRAD STATUS=INITIATE 14 CALLS 15 TOTAL
EDM= unknown STRATEGY= 1 NO ERROR MATRIX
EXT PARAMETER CURRENT GUESS STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 mu_x0 0.00000e+00 4.00000e-01 2.01358e-01 -9.83942e+00
2 mu_x1 0.00000e+00 4.00000e-01 2.01358e-01 -1.25127e+01
3 mu_x2 0.00000e+00 4.00000e-01 2.01358e-01 9.88572e+00
4 mu_x3 0.00000e+00 4.00000e-01 2.01358e-01 -4.09155e+00
ERR DEF= 0.5
MIGRAD MINIMIZATION HAS CONVERGED.
MIGRAD WILL VERIFY CONVERGENCE AND ERROR MATRIX.
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=706.56 FROM MIGRAD STATUS=CONVERGED 65 CALLS 66 TOTAL
EDM=1.95881e-05 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER STEP FIRST
NO. NAME VALUE ERROR SIZE DERIVATIVE
1 mu_x0 1.80728e-01 1.72980e-01 1.42731e-03 -2.59592e-02
2 mu_x1 2.07351e-01 1.72978e-01 1.42884e-03 -3.69006e-02
3 mu_x2 -1.59412e-02 1.72984e-01 1.42230e-03 3.21539e-02
4 mu_x3 1.23430e-01 1.72982e-01 1.42472e-03 -8.04153e-03
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 4 ERR DEF=0.5
3.000e-02 9.997e-03 9.998e-03 9.997e-03
9.997e-03 3.000e-02 9.998e-03 9.997e-03
9.998e-03 9.998e-03 3.000e-02 9.998e-03
9.997e-03 9.997e-03 9.998e-03 3.000e-02
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2 3 4
1 0.44715 1.000 0.333 0.333 0.333
2 0.44715 0.333 1.000 0.333 0.333
3 0.44717 0.333 0.333 1.000 0.333
4 0.44716 0.333 0.333 0.333 1.000
**********
** 7 **SET ERR 0.5
**********
**********
** 8 **SET PRINT 1
**********
**********
** 9 **HESSE 2000
**********
COVARIANCE MATRIX CALCULATED SUCCESSFULLY
FCN=706.56 FROM HESSE STATUS=OK 23 CALLS 89 TOTAL
EDM=1.95881e-05 STRATEGY= 1 ERROR MATRIX ACCURATE
EXT PARAMETER INTERNAL INTERNAL
NO. NAME VALUE ERROR STEP SIZE VALUE
1 mu_x0 1.80728e-01 1.72984e-01 2.85462e-04 9.04875e-02
2 mu_x1 2.07351e-01 1.72982e-01 2.85769e-04 1.03862e-01
3 mu_x2 -1.59412e-02 1.72987e-01 2.84460e-04 -7.97069e-03
4 mu_x3 1.23430e-01 1.72986e-01 2.84944e-04 6.17540e-02
ERR DEF= 0.5
EXTERNAL ERROR MATRIX. NDIM= 25 NPAR= 4 ERR DEF=0.5
3.000e-02 9.999e-03 9.999e-03 9.999e-03
9.999e-03 3.000e-02 9.999e-03 9.999e-03
9.999e-03 9.999e-03 3.000e-02 9.999e-03
9.999e-03 9.999e-03 9.999e-03 3.000e-02
PARAMETER CORRELATION COEFFICIENTS
NO. GLOBAL 1 2 3 4
1 0.44720 1.000 0.333 0.333 0.333
2 0.44719 0.333 1.000 0.333 0.333
3 0.44720 0.333 0.333 1.000 0.333
4 0.44720 0.333 0.333 0.333 1.000
[#1] INFO:Minization -- RooMinimizer::optimizeConst: deactivating const optimization
[#1] INFO:Minization -- createNLL: caching constraint set under name CONSTR_OF_PDF_mvg_FOR_OBS_x0:x1:x2:x3 with 0 entries
Metropolis-Hastings progress: ....................................................................................................
[#1] INFO:Eval -- Proposal acceptance rate: 37.1%
[#1] INFO:Eval -- Number of steps in chain: 3710
[#1] INFO:Minization -- createNLL picked up cached consraints from workspace with 0 entries
[#0] PROGRESS:Minization -- ProfileLikelihoodCalcultor::DoGLobalFit - find MLE
[#0] PROGRESS:Minization -- ProfileLikelihoodCalcultor::DoMinimizeNLL - using Minuit / Migrad with strategy 1
[#1] INFO:Minization -- RooMinimizer::optimizeConst: activating const optimization
[#1] INFO:Minization --
RooFitResult: minimized FCN value: 706.56, estimated distance to minimum: 1.16082e-08
covariance matrix quality: Full, accurate covariance matrix
Status : MINIMIZE=0
Floating Parameter FinalValue +/- Error
-------------------- --------------------------
mu_x0 1.8119e-01 +/- 1.73e-01
mu_x1 2.0792e-01 +/- 1.73e-01
mu_x2 -1.6078e-02 +/- 1.73e-01
mu_x3 1.2370e-01 +/- 1.73e-01
[#1] INFO:Minization -- RooProfileLL::evaluate(nll_mvg_mvgData_Profile[mu_x0,mu_x1]) Creating instance of MINUIT
[#1] INFO:Minization -- RooProfileLL::evaluate(nll_mvg_mvgData_Profile[mu_x0,mu_x1]) determining minimum likelihood for current configurations w.r.t all observable
[#1] INFO:Minization -- RooProfileLL::evaluate(nll_mvg_mvgData_Profile[mu_x0,mu_x1]) minimum found at (mu_x0=0.181184, mu_x1=0.207917)
..[#1] INFO:Minization -- LikelihoodInterval - Finding the contour of mu_x0 ( 0 ) and mu_x1 ( 1 )
MCMC interval on p0: [-0.28, 0.6]
MCMC interval on p1: [-0.28, 0.6]
Real time 0:00:02, CP time 2.020
#include <stdlib.h>
void MultivariateGaussianTest(
Int_t dim = 4,
Int_t nPOI = 2)
{
for (i = 0; i < dim; i++) {
char* mu_name =
Form(
"mu_x%d",i);
}
for (i = 0; i < nPOI; i++) {
}
for (i = 0; i < dim; i++) {
for (j = 0; j < dim; j++) {
if (i == j) cov(i,j) = 3.;
else cov(i,j) = 1.0;
}
}
ModelConfig modelConfig(w);
modelConfig.SetPdf(mvg);
modelConfig.SetParametersOfInterest(poi);
ProposalHelper ph;
ph.SetUpdateProposalParameters(true);
ph.SetCacheSize(100);
ProposalFunction* pdfProp = ph.GetProposalFunction();
MCMCCalculator mc(*
data, modelConfig);
mc.SetConfidenceLevel(0.95);
mc.SetNumBurnInSteps(100);
mc.SetNumIters(10000);
mc.SetNumBins(50);
mc.SetProposalFunction(*pdfProp);
MCMCInterval* mcInt = mc.GetInterval();
ProfileLikelihoodCalculator plc(*
data, modelConfig);
plc.SetConfidenceLevel(0.95);
LikelihoodInterval* plInt = (LikelihoodInterval*)plc.GetInterval();
MCMCIntervalPlot mcPlot(*mcInt);
mcPlot.SetLineWidth(2);
mcPlot.Draw();
LikelihoodIntervalPlot plPlot(plInt);
plPlot.Draw("same");
cout << "MCMC interval: [" << ll << ", " << ul << "]" << endl;
}
cout << "MCMC interval on p0: [" << ll << ", " << ul << "]" << endl;
ll = mcInt->LowerLimit(*p0);
ul = mcInt->UpperLimit(*p0);
cout << "MCMC interval on p1: [" << ll << ", " << ul << "]" << endl;
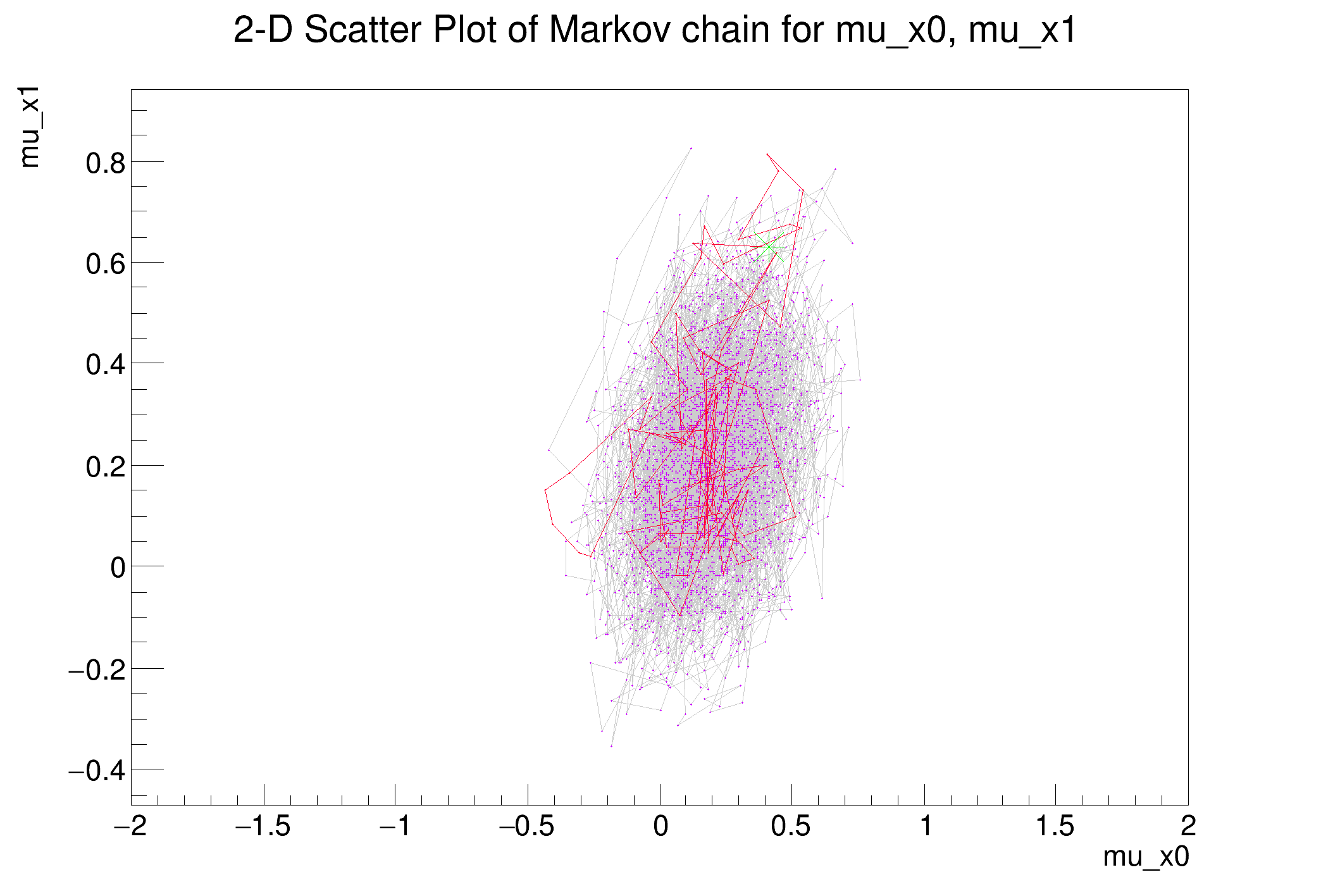
mcPlot.DrawChainScatter(*p0, *
p1);
}
}
static double p1(double t, double a, double b)
char * Form(const char *fmt,...)
virtual Bool_t add(const RooAbsArg &var, Bool_t silent=kFALSE)
Add the specified argument to list.
RooAbsArg * at(Int_t idx) const
RooArgSet is a container object that can hold multiple RooAbsArg objects.
virtual Bool_t add(const RooAbsCollection &col, Bool_t silent=kFALSE)
Add a collection of arguments to this collection by calling add() for each element in the source coll...
RooDataSet is a container class to hold unbinned data.
RooFitResult is a container class to hold the input and output of a PDF fit to a dataset.
const TMatrixDSym & covarianceMatrix() const
Return covariance matrix.
const RooArgList & floatParsFinal() const
Multivariate Gaussian p.d.f.
RooRealVar represents a fundamental (non-derived) real valued object.
The RooWorkspace is a persistable container for RooFit projects.
virtual void Update()
Update canvas pad buffers.
void Start(Bool_t reset=kTRUE)
Start the stopwatch.
void Print(Option_t *option="") const
Print the real and cpu time passed between the start and stop events.
RooCmdArg Save(Bool_t flag=kTRUE)
@(#)root/roostats:$Id$ Author: George Lewis, Kyle Cranmer



 Comparison of MCMC and PLC in a multi-variate gaussian problem
Comparison of MCMC and PLC in a multi-variate gaussian problem