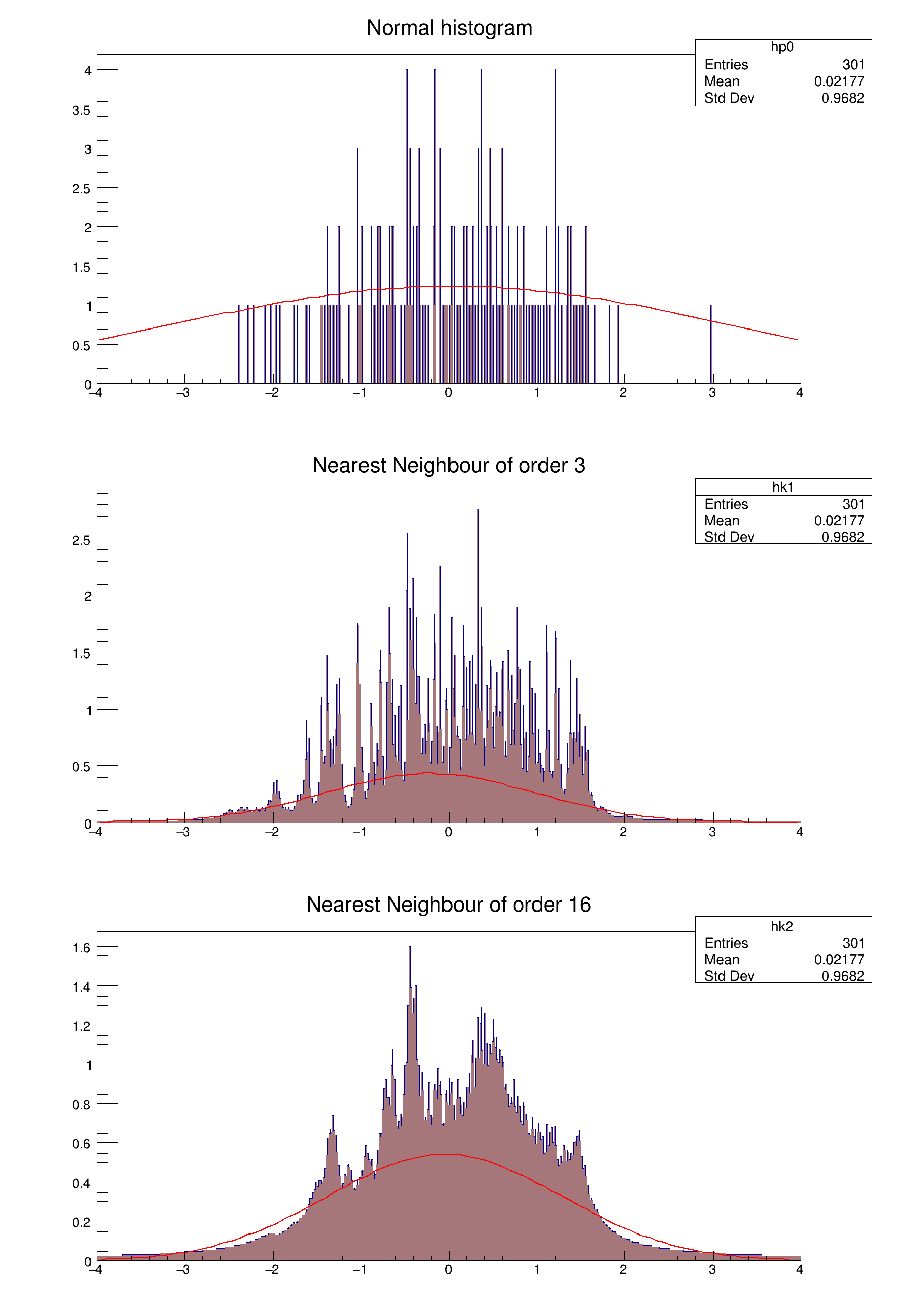
Illustrates the advantages of a TH1K histogram
Illustrates the advantages of a TH1K histogram
void padRefresh(
TPad *pad,
int flag=0)
{
if (!pad) return;
if (!tl) return;
while ((to=next())) {
if (flag) return;
}
void hksimple()
{
TCanvas* c1 =
new TCanvas(
"c1",
"Dynamic Filling Example",200,10,600,900);
hpx[0] =
new TH1F(
"hp0",
"Normal histogram",1000,-4,4);
hpx[1] =
new TH1K(
"hk1",
"Nearest Neighbour of order 3",1000,-4,4);
hpx[2] =
new TH1K(
"hk2",
"Nearest Neighbour of order 16",1000,-4,4,16);
for (j=0;j<3;j++) {
}
const Int_t kUPDATE = 10;
for (
Int_t i = 0; i <= 300; i++) {
for (j=0;j<3;j++) {hpx[j]->
Fill(px);}
if (i && (i%kUPDATE) == 0) {
padRefresh(c1);
}
}
for (j=0;j<3;j++) hpx[j]->
Fit(
"gaus");
padRefresh(c1);
}
- Author
- Victor Perevovchikov
Definition in file hksimple.C.



 Illustrates the advantages of a TH1K histogram
Illustrates the advantages of a TH1K histogram