Multidimensional Fits in ROOT.

Overview

A common problem encountered in different fields of applied science is to find an expression for one physical quantity in terms of several others, which are directly measurable.

An example in high energy physics is the evaluation of the momentum of a charged particle from the observation of its trajectory in a magnetic field. The problem is to relate the momentum of the particle to the observations, which may consists of positional measurements at intervals along the particle trajectory.

The exact functional relationship between the measured quantities (e.g., the space-points) and the dependent quantity (e.g., the momentum) is in general not known, but one possible way of solving the problem, is to find an expression which reliably approximates the dependence of the momentum on the observations.

This explicit function of the observations can be obtained by a least squares fitting procedure applied to a representative sample of the data, for which the dependent quantity (e.g., momentum) and the independent observations are known. The function can then be used to compute the quantity of interest for new observations of the independent variables.

This class TMultiDimFit implements such a procedure in ROOT. It is largely based on the CERNLIB MUDIFI package 2. Though the basic concepts are still sound, and therefore kept, a few implementation details have changed, and this class can take advantage of MINUIT 4 to improve the errors of the fitting, thanks to the class TMinuit.

In 5 and 6 H. Wind demonstrates the utility of this procedure in the context of tracking, magnetic field parameterisation, and so on. The outline of the method used in this class is based on Winds discussion, and I refer these two excellents text for more information.

And example of usage is given in multidimfit.C.

The Method

Let $ D $ by the dependent quantity of interest, which depends smoothly on the observable quantities $ x_1, \ldots, x_N $ which we'll denote by $\mathbf{x}$. Given a training sample of $ M$ tuples of the form, (TMultiDimFit::AddRow)

\[ \left(\mathbf{x}_j, D_j, E_j\right)\quad, \]

where $\mathbf{x}_j = (x_{1,j},\ldots,x_{N,j})$ are $ N$ independent variables, $ D_j$ is the known, quantity dependent at $\mathbf{x}_j$ and $ E_j$ is the square error in $ D_j$, the class will try to find the parameterization

\[ D_p(\mathbf{x}) = \sum_{l=1}^{L} c_l \prod_{i=1}^{N} p_{li}\left(x_i\right) = \sum_{l=1}^{L} c_l F_l(\mathbf{x}) \]

such that

\[ S \equiv \sum_{j=1}^{M} \left(D_j - D_p\left(\mathbf{x}_j\right)\right)^2 \]

is minimal. Here $p_{li}(x_i)$ are monomials, or Chebyshev or Legendre polynomials, labelled $l = 1, \ldots, L$, in each variable $ x_i$, $ i=1, \ldots, N$.

So what TMultiDimFit does, is to determine the number of terms $ L$, and then $ L$ terms (or functions) $ F_l$, and the $ L$ coefficients $ c_l$, so that $ S$ is minimal (TMultiDimFit::FindParameterization).

Of course it's more than a little unlikely that $ S$ will ever become exact zero as a result of the procedure outlined below. Therefore, the user is asked to provide a minimum relative error $ \epsilon$ (TMultiDimFit::SetMinRelativeError), and $ S$ will be considered minimized when

\[ R = \frac{S}{\sum_{j=1}^M D_j^2} < \epsilon \]

Optionally, the user may impose a functional expression by specifying the powers of each variable in $ L$ specified functions $ F_1, \ldots,F_L$ (TMultiDimFit::SetPowers). In that case, only the coefficients $ c_l$ is calculated by the class.

Limiting the Number of Terms

As always when dealing with fits, there's a real chance of over fitting. As is well-known, it's always possible to fit an $ N-1$ polynomial in $ x$ to $ N$ points $ (x,y)$ with $\chi^2 = 0$, but the polynomial is not likely to fit new data at all 1. Therefore, the user is asked to provide an upper limit, $ L_{max}$ to the number of terms in $ D_p$ (TMultiDimFit::SetMaxTerms).

However, since there's an infinite number of $ F_l$ to choose from, the user is asked to give the maximum power. $ P_{max,i}$, of each variable $ x_i$ to be considered in the minimization of $ S$ (TMultiDimFit::SetMaxPowers).

One way of obtaining values for the maximum power in variable $ i$, is to perform a regular fit to the dependent quantity $ D$, using a polynomial only in $ x_i$. The maximum power is $ P_{max,i}$ is then the power that does not significantly improve the one-dimensional least-square fit over $ x_i$ to $ D$ 5.

There are still a huge amount of possible choices for $ F_l$; in fact there are $\prod_{i=1}^{N} (P_{max,i} + 1)$ possible choices. Obviously we need to limit this. To this end, the user is asked to set a power control limit, $ Q$ (TMultiDimFit::SetPowerLimit), and a function $ F_l$ is only accepted if

\[ Q_l = \sum_{i=1}^{N} \frac{P_{li}}{P_{max,i}} < Q \]

where $ P_{li}$ is the leading power of variable $ x_i$ in function $ F_l$ (TMultiDimFit::MakeCandidates). So the number of functions increase with $ Q$ (1, 2 is fine, 5 is way out).

Gram-Schmidt Orthogonalisation

To further reduce the number of functions in the final expression, only those functions that significantly reduce $ S$ is chosen. What `significant' means, is chosen by the user, and will be discussed below (see 2.3).

The functions $ F_l$ are generally not orthogonal, which means one will have to evaluate all possible $ F_l$'s over all data-points before finding the most significant 1. We can, however, do better then that. By applying the modified Gram-Schmidt orthogonalisation algorithm [5] [3] to the functions $ F_l$, we can evaluate the contribution to the reduction of $ S$ from each function in turn, and we may delay the actual inversion of the curvature-matrix (TMultiDimFit::MakeGramSchmidt).

So we are let to consider an $ M\times L$ matrix $\mathsf{F}$, an element of which is given by

\[ f_{jl} = F_j\left(x_{1j} , x_{2j}, \ldots, x_{Nj}\right) = F_l(\mathbf{x}_j)\, \quad\mbox{with}~j=1,2,\ldots,M, \]

where $ j$ labels the $ M$ rows in the training sample and $ l$ labels $ L$ functions of $ N$ variables, and $ L \leq M$. That is, $ f_{jl}$ is the term (or function) numbered $ l$ evaluated at the data point $ j$. We have to normalise $\mathbf{x}_j$ to $ [-1,1]$ for this to succeed [5] (TMultiDimFit::MakeNormalized). We then define a matrix $\mathsf{W}$ of which the columns $\mathbf{w}_j$ are given by

\begin{eqnarray*} \mathbf{w}_1 &=& \mathbf{f}_1 = F_1\left(\mathbf x_1\right)\\ \mathbf{w}_l &=& \mathbf{f}_l - \sum^{l-1}_{k=1} \frac{\mathbf{f}_l \bullet \mathbf{w}_k}{\mathbf{w}_k^2}\mathbf{w}_k\,. \end{eqnarray*}

and $\mathbf{w}_{l}$ is the component of $\mathbf{f}_{l} $ orthogonal to $\mathbf{w}_{1}, \ldots, \mathbf{w}_{l-1}$. Hence we obtain [3],

\[ \mathbf{w}_k\bullet\mathbf{w}_l = 0\quad\mbox{if}~k \neq l\quad. \]

We now take as a new model $\mathsf{W}\mathbf{a}$. We thus want to minimize

\[ S\equiv \left(\mathbf{D} - \mathsf{W}\mathbf{a}\right)^2\quad, \]

where $\mathbf{D} = \left(D_1,\ldots,D_M\right)$ is a vector of the dependent quantity in the sample. Differentiation with respect to $ a_j$ gives, using 6,

\[ \mathbf{D}\bullet\mathbf{w}_l - a_l\mathbf{w}_l^2 = 0 \]

or

\[ a_l = \frac{\mathbf{D}_l\bullet\mathbf{w}_l}{\mathbf{w}_l^2} \]

Let $ S_j$ be the sum of squares of residuals when taking $ j$ functions into account. Then

\[ S_l = \left[\mathbf{D} - \sum^l_{k=1} a_k\mathbf{w}_k\right]^2 = \mathbf{D}^2 - 2\mathbf{D} \sum^l_{k=1} a_k\mathbf{w}_k + \sum^l_{k=1} a_k^2\mathbf{w}_k^2 \]

Using 9, we see that

\begin{eqnarray*} S_l &=& \mathbf{D}^2 - 2 \sum^l_{k=1} a_k^2\mathbf{w}_k^2 + \sum^j_{k=1} a_k^2\mathbf{w}_k^2\nonumber\\ &=& \mathbf{D}^2 - \sum^l_{k=1} a_k^2\mathbf{w}_k^2\nonumber\\ &=& \mathbf{D}^2 - \sum^l_{k=1} \frac{\left(\mathbf D\bullet \mathbf w_k\right)}{\mathbf w_k^2} \end{eqnarray*}

So for each new function $ F_l$ included in the model, we get a reduction of the sum of squares of residuals of $a_l^2\mathbf{w}_l^2$, where $\mathbf{w}_l$ is given by 4 and $ a_l$ by 9. Thus, using the Gram-Schmidt orthogonalisation, we can decide if we want to include this function in the final model, before* the matrix inversion.

Function Selection Based on Residual

Supposing that $ L-1$ steps of the procedure have been performed, the problem now is to consider the $L^{\mbox{th}}$ function.

The sum of squares of residuals can be written as

\[ S_L = \textbf{D}^T\bullet\textbf{D} - \sum^L_{l=1}a^2_l\left(\textbf{w}_l^T\bullet\textbf{w}_l\right) \]

where the relation 9 have been taken into account. The contribution of the $L^{\mbox{th}}$ function to the reduction of S, is given by

\[ \Delta S_L = a^2_L\left(\textbf{w}_L^T\bullet\textbf{w}_L\right) \]

Two test are now applied to decide whether this $L^{\mbox{th}}$ function is to be included in the final expression, or not.

Test 1

Denoting by $ H_{L-1}$ the subspace spanned by $\textbf{w}_1,\ldots,\textbf{w}_{L-1}$ the function ${w}_L$ is by construction (see 4) the projection of the function $ F_L$ onto the direction perpendicular to $ H_{L-1}$. Now, if the length of $\textbf{w}_L$ (given by $\textbf{w}_L\bullet\textbf{w}_L$) is very small compared to the length of $\textbf{f}_L$ this new function can not contribute much to the reduction of the sum of squares of residuals. The test consists then in calculating the angle $ \theta $ between the two vectors $\textbf{w}_L$ $ \textbf {f}_L$ (see also figure 1) and requiring that it's greater* then a threshold value which the user must set (TMultiDimFit::SetMinAngle).

Figure 1: (a) angle $$ between ${w}_l$ and ${f}_L$, (b) angle $ $ between ${w}_L$ and ${D}$

Test 2

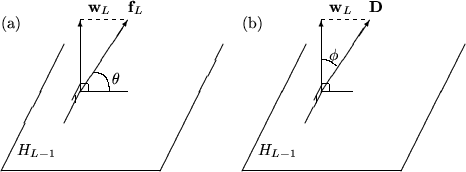
Let $\textbf{D}$ be the data vector to be fitted. As illustrated in figure 1, the $L^{\mbox{th}}$ function $\textbf{w}_L$ will contribute significantly to the reduction of $ S$, if the angle $\phi^\prime$ between $\textbf{w}_L$ and $\textbf{D}$ is smaller than an upper limit $ \phi $, defined by the user (MultiDimFit::SetMaxAngle)

However, the method automatically readjusts the value of this angle while fitting is in progress, in order to make the selection criteria less and less difficult to be fulfilled. The result is that the functions contributing most to the reduction of $ S$ are chosen first (TMultiDimFit::TestFunction).

In case $ \phi $ isn't defined, an alternative method of performing this second test is used: The $L^{\mbox{th}}$ function $\textbf{f}_L$ is accepted if (refer also to equation (13))

\[ \Delta S_L > \frac{S_{L-1}}{L_{max}-L} \]

where $ S_{L-1}$ is the sum of the $ L-1$ first residuals from the $ L-1$ functions previously accepted; and $ L_{max}$ is the total number of functions allowed in the final expression of the fit (defined by user).

From this we see, that by restricting $ L_{max}$ – the number of terms in the final model – the fit is more difficult to perform, since the above selection criteria is more limiting.

The more coefficients we evaluate, the more the sum of squares of residuals $ S$ will be reduced. We can evaluate $ S$ before inverting $\mathsf{B}$ as shown below.

Coefficients and Coefficient Errors

Having found a parameterization, that is the $ F_l$'s and $ L$, that minimizes $ S$, we still need to determine the coefficients $ c_l$. However, it's a feature of how we choose the significant functions, that the evaluation of the $ c_l$'s becomes trivial 5. To derive $\mathbf{c}$, we first note that equation (4) can be written as

\[ \mathsf{F} = \mathsf{W}\mathsf{B} \]

where

\begin{eqnarray*} b_{ij} = \frac{\mathbf{f}_j \bullet \mathbf{w}_i}{\mathbf{w}_i^2} & \mbox{if} & i < j\\ 1 & \mbox{if} & i = j\\ 0 & \mbox{if} & i > j \end{eqnarray*}

Consequently, $\mathsf{B}$ is an upper triangle matrix, which can be readily inverted. So we now evaluate

\[ \mathsf{F}\mathsf{B}^{-1} = \mathsf{W} \]

The model $\mathsf{W}\mathbf{a}$ can therefore be written as $(\mathsf{F}\mathsf{B}^{-1})\mathbf{a} = \mathsf{F}(\mathsf{B}^{-1}\mathbf{a})\,.$

The original model $\mathsf{F}\mathbf{c}$ is therefore identical with this if

\[ \mathbf{c} = \left(\mathsf{B}^{-1}\mathbf{a}\right) = \left[\mathbf{a}^T\left(\mathsf{B}^{-1}\right)^T\right]^T\,. \]

The reason we use $\left(\mathsf{B}^{-1}\right)^T$ rather then $\mathsf{B}^{-1}$ is to save storage, since $\left(\mathsf{B}^{-1}\right)^T$ can be stored in the same matrix as $\mathsf{B}$ (TMultiDimFit::MakeCoefficients). The errors in the coefficients is calculated by inverting the curvature matrix of the non-orthogonal functions $ f_{lj}$ [1] (TMultiDimFit::MakeCoefficientErrors).

Considerations

It's important to realize that the training sample should be representative of the problem at hand, in particular along the borders of the region of interest. This is because the algorithm presented here, is a interpolation, rather then a extrapolation 5.

Also, the independent variables $ x_{i}$ need to be linear independent, since the procedure will perform poorly if they are not 5. One can find an linear transformation from ones original variables $ \xi_{i}$ to a set of linear independent variables $ x_{i}$, using a Principal Components Analysis (see TPrincipal), and then use the transformed variable as input to this class 5.

H. Wind also outlines a method for parameterising a multidimensional dependence over a multidimensional set of variables. An example of the method from 5, is a follows (please refer to 5 for a full discussion):

Define $\mathbf{P} = (P_1, \ldots, P_5)$ are the 5 dependent quantities that define a track.
Compute, for $ M$ different values of $\mathbf{P}$, the tracks through the magnetic field, and determine the corresponding $\mathbf{x} = (x_1, \ldots, x_N)$.
Use the simulated observations to determine, with a simple approximation, the values of $\mathbf{P}_j$. We call these values $\mathbf{P}^\prime_j, j = 1, \ldots, M$.
Determine from $\mathbf{x}$ a set of at least five relevant coordinates $\mathbf{x}^\prime$, using contrains, or alternative:
Perform a Principal Component Analysis (using TPrincipal), and use to get a linear transformation $\mathbf{x} \rightarrow \mathbf{x}^\prime$, so that $\mathbf{x}^\prime$ are constrained and linear independent.
Perform a Principal Component Analysis on $Q_i = P_i / P^\prime_i\, i = 1, \ldots, 5$, to get linear indenpendent (among themselves, but not independent of $\mathbf{x}$) quantities $\mathbf{Q}^\prime$
For each component $Q^\prime_i$ make a multidimensional fit, using $\mathbf{x}^\prime$ as the variables, thus determining a set of coefficients $\mathbf{c}_i$.

To process data, using this parameterisation, do

Test wether the observation $\mathbf{x}$ within the domain of the parameterization, using the result from the Principal Component Analysis.
Determine $\mathbf{P}^\prime$ as before.
Determine $\mathbf{x}^\prime$ as before.
Use the result of the fit to determine $\mathbf{Q}^\prime$.
Transform back to $\mathbf{P}$ from $\mathbf{Q}^\prime$, using the result from the Principal Component Analysis.

Testing the parameterization

The class also provides functionality for testing the, over the training sample, found parameterization (TMultiDimFit::Fit). This is done by passing the class a test sample of $ M_t$ tuples of the form $(\mathbf{x}_{t,j},D_{t,j}, E_{t,j})$, where $\mathbf{x}_{t,j}$ are the independent variables, $ D_{t,j}$ the known, dependent quantity, and $ E_{t,j}$ is the square error in $ D_{t,j}$ (TMultiDimFit::AddTestRow).

The parameterization is then evaluated at every $\mathbf{x}_t$ in the test sample, and

\[ S_t \equiv \sum_{j=1}^{M_t} \left(D_{t,j} - D_p\left(\mathbf{x}_{t,j}\right)\right)^2 \]

is evaluated. The relative error over the test sample

\[ R_t = \frac{S_t}{\sum_{j=1}^{M_t} D_{t,j}^2} \]

should not be to low or high compared to $ R$ from the training sample. Also, multiple correlation coefficient from both samples should be fairly close, otherwise one of the samples is not representative of the problem. A large difference in the reduced $ \chi^2$ over the two samples indicate an over fit, and the maximum number of terms in the parameterisation should be reduced.

It's possible to use 4 to further improve the fit, using the test sample.

Christian Holm

Bibliography

Philip R. Bevington and D. Keith Robinson. Data Reduction and Error Analysis for the Physical Sciences. McGraw-Hill, 2 edition, 1992.
R. Brun et al. Long writeup DD/75-23, CERN, 1980.
Gene H. Golub and Charles F. van Loan. Matrix Computations. John Hopkins University Press, Baltimore, 3 edition, 1996.
F. James. Minuit. Long writeup D506, CERN, 1998.
H. Wind. Function parameterization. Proceedings of the 1972 CERN Computing and Data Processing School, volume 72-21 of Yellow report. CERN, 1972.
H. Wind. 1. principal component analysis, 2. pattern recognition for track finding, 3. interpolation and functional representation. Yellow report EP/81-12, CERN, 1981.

Definition at line 15 of file TMultiDimFit.h.

Public Types
enum	EMDFPolyType { kMonomials, kChebyshev, kLegendre }

Public Types inherited from TObject
enum	{ kIsOnHeap = 0x01000000, kNotDeleted = 0x02000000, kZombie = 0x04000000, kInconsistent = 0x08000000, kBitMask = 0x00ffffff }

enum	{ kSingleKey = BIT(0), kOverwrite = BIT(1), kWriteDelete = BIT(2) }

enum	EDeprecatedStatusBits { kObjInCanvas = BIT(3) }

enum	EStatusBits { kCanDelete = BIT(0), kMustCleanup = BIT(3), kIsReferenced = BIT(4), kHasUUID = BIT(5), kCannotPick = BIT(6), kNoContextMenu = BIT(8), kInvalidObject = BIT(13) }

Public Member Functions
	TMultiDimFit ()
	Empty CTOR. Do not use. More...

	TMultiDimFit (Int_t dimension, EMDFPolyType type=kMonomials, Option_t *option="")
	Constructor Second argument is the type of polynomials to use in parameterisation, one of: TMultiDimFit::kMonomials TMultiDimFit::kChebyshev TMultiDimFit::kLegendre. More...

virtual	~TMultiDimFit ()
	Destructor. More...

virtual void	AddRow (const Double_t *x, Double_t D, Double_t E=0)
	Add a row consisting of fNVariables independent variables, the known, dependent quantity, and optionally, the square error in the dependent quantity, to the training sample to be used for the parameterization. More...

virtual void	AddTestRow (const Double_t *x, Double_t D, Double_t E=0)
	Add a row consisting of fNVariables independent variables, the known, dependent quantity, and optionally, the square error in the dependent quantity, to the test sample to be used for the test of the parameterization. More...

virtual void	Browse (TBrowser *b)
	Browse the TMultiDimFit object in the TBrowser. More...

virtual void	Clear (Option_t *option="")
	Clear internal structures and variables. More...

virtual void	Draw (Option_t *="d")
	Default Draw method for all objects. More...

virtual Double_t	Eval (const Double_t x, const Double_t coeff=0) const
	Evaluate parameterization at point x. More...

virtual Double_t	EvalError (const Double_t x, const Double_t coeff=0) const
	Evaluate parameterization error at point x. More...

virtual void	FindParameterization (Option_t *option="")
	Find the parameterization. More...

virtual void	Fit (Option_t *option="")
	Try to fit the found parameterisation to the test sample. More...

Double_t	GetChi2 () const

const TVectorD *	GetCoefficients () const

const TVectorD *	GetCoefficientsRMS () const

const TMatrixD *	GetCorrelationMatrix () const

Double_t	GetError () const

Int_t *	GetFunctionCodes () const

const TMatrixD *	GetFunctions () const

virtual TList *	GetHistograms () const

Double_t	GetMaxAngle () const

Int_t	GetMaxFunctions () const

Int_t *	GetMaxPowers () const

Double_t	GetMaxQuantity () const

Int_t	GetMaxStudy () const

Int_t	GetMaxTerms () const

const TVectorD *	GetMaxVariables () const

Double_t	GetMeanQuantity () const

const TVectorD *	GetMeanVariables () const

Double_t	GetMinAngle () const

Double_t	GetMinQuantity () const

Double_t	GetMinRelativeError () const

const TVectorD *	GetMinVariables () const

Int_t	GetNCoefficients () const

Int_t	GetNVariables () const

Int_t	GetPolyType () const

Int_t *	GetPowerIndex () const

Double_t	GetPowerLimit () const

const Int_t *	GetPowers () const

Double_t	GetPrecision () const

const TVectorD *	GetQuantity () const

Double_t	GetResidualMax () const

Int_t	GetResidualMaxRow () const

Double_t	GetResidualMin () const

Int_t	GetResidualMinRow () const

Double_t	GetResidualSumSq () const

Double_t	GetRMS () const

Int_t	GetSampleSize () const

const TVectorD *	GetSqError () const

Double_t	GetSumSqAvgQuantity () const

Double_t	GetSumSqQuantity () const

Double_t	GetTestError () const

Double_t	GetTestPrecision () const

const TVectorD *	GetTestQuantity () const

Int_t	GetTestSampleSize () const

const TVectorD *	GetTestSqError () const

const TVectorD *	GetTestVariables () const

const TVectorD *	GetVariables () const

virtual Bool_t	IsFolder () const
	Returns kTRUE in case object contains browsable objects (like containers or lists of other objects). More...

virtual Double_t	MakeChi2 (const Double_t *coeff=0)
	Calculate Chi square over either the test sample. More...

virtual void	MakeCode (const char functionName="MDF", Option_t option="")
	Generate the file <filename> with .C appended if argument doesn't end in .cxx or .C. More...

virtual void	MakeHistograms (Option_t *option="A")
	Make histograms of the result of the analysis. More...

virtual void	MakeMethod (const Char_t className="MDF", Option_t option="")
	Generate the file <classname>MDF.cxx which contains the implementation of the method: More...

virtual void	Print (Option_t *option="ps") const
	Print statistics etc. More...

void	SetBinVarX (Int_t nbbinvarx)

void	SetBinVarY (Int_t nbbinvary)

void	SetMaxAngle (Double_t angle=0)
	Set the max angle (in degrees) between the initial data vector to be fitted, and the new candidate function to be included in the fit. More...

void	SetMaxFunctions (Int_t n)

void	SetMaxPowers (const Int_t *powers)
	Set the maximum power to be considered in the fit for each variable. More...

void	SetMaxStudy (Int_t n)

void	SetMaxTerms (Int_t terms)

void	SetMinAngle (Double_t angle=1)
	Set the min angle (in degrees) between a new candidate function and the subspace spanned by the previously accepted functions. More...

void	SetMinRelativeError (Double_t error)
	Set the acceptable relative error for when sum of square residuals is considered minimized. More...

void	SetPowerLimit (Double_t limit=1e-3)
	Set the user parameter for the function selection. More...

virtual void	SetPowers (const Int_t *powers, Int_t terms)
	Define a user function. More...

Public Member Functions inherited from TNamed
	TNamed ()

	TNamed (const char name, const char title)

	TNamed (const TString &name, const TString &title)

	TNamed (const TNamed &named)
	TNamed copy ctor. More...

virtual	~TNamed ()
	TNamed destructor. More...

virtual TObject *	Clone (const char *newname="") const
	Make a clone of an object using the Streamer facility. More...

virtual Int_t	Compare (const TObject *obj) const
	Compare two TNamed objects. More...

virtual void	Copy (TObject &named) const
	Copy this to obj. More...

virtual void	FillBuffer (char *&buffer)
	Encode TNamed into output buffer. More...

virtual const char *	GetName () const
	Returns name of object. More...

virtual const char *	GetTitle () const
	Returns title of object. More...

virtual ULong_t	Hash () const
	Return hash value for this object. More...

virtual Bool_t	IsSortable () const

virtual void	ls (Option_t *option="") const
	List TNamed name and title. More...

TNamed &	operator= (const TNamed &rhs)
	TNamed assignment operator. More...

virtual void	SetName (const char *name)
	Set the name of the TNamed. More...

virtual void	SetNameTitle (const char name, const char title)
	Set all the TNamed parameters (name and title). More...

virtual void	SetTitle (const char *title="")
	Set the title of the TNamed. More...

virtual Int_t	Sizeof () const
	Return size of the TNamed part of the TObject. More...

Public Member Functions inherited from TObject
	TObject ()
	TObject constructor. More...

	TObject (const TObject &object)
	TObject copy ctor. More...

virtual	~TObject ()
	TObject destructor. More...

void	AbstractMethod (const char *method) const
	Use this method to implement an "abstract" method that you don't want to leave purely abstract. More...

virtual void	AppendPad (Option_t *option="")
	Append graphics object to current pad. More...

ULong_t	CheckedHash ()
	Checked and record whether for this class has a consistent Hash/RecursiveRemove setup (*) and then return the regular Hash value for this object. More...

virtual const char *	ClassName () const
	Returns name of class to which the object belongs. More...

virtual void	Delete (Option_t *option="")
	Delete this object. More...

virtual Int_t	DistancetoPrimitive (Int_t px, Int_t py)
	Computes distance from point (px,py) to the object. More...

virtual void	DrawClass () const
	Draw class inheritance tree of the class to which this object belongs. More...

virtual TObject *	DrawClone (Option_t *option="") const
	Draw a clone of this object in the current selected pad for instance with: `gROOT->SetSelectedPad(gPad)`. More...

virtual void	Dump () const
	Dump contents of object on stdout. More...

virtual void	Error (const char method, const char msgfmt,...) const
	Issue error message. More...

virtual void	Execute (const char method, const char params, Int_t *error=0)
	Execute method on this object with the given parameter string, e.g. More...

virtual void	Execute (TMethod method, TObjArray params, Int_t *error=0)
	Execute method on this object with parameters stored in the TObjArray. More...

virtual void	ExecuteEvent (Int_t event, Int_t px, Int_t py)
	Execute action corresponding to an event at (px,py). More...

virtual void	Fatal (const char method, const char msgfmt,...) const
	Issue fatal error message. More...

virtual TObject *	FindObject (const char *name) const
	Must be redefined in derived classes. More...

virtual TObject *	FindObject (const TObject *obj) const
	Must be redefined in derived classes. More...

virtual Option_t *	GetDrawOption () const
	Get option used by the graphics system to draw this object. More...

virtual const char *	GetIconName () const
	Returns mime type name of object. More...

virtual char *	GetObjectInfo (Int_t px, Int_t py) const
	Returns string containing info about the object at position (px,py). More...

virtual Option_t *	GetOption () const

virtual UInt_t	GetUniqueID () const
	Return the unique object id. More...

virtual Bool_t	HandleTimer (TTimer *timer)
	Execute action in response of a timer timing out. More...

Bool_t	HasInconsistentHash () const
	Return true is the type of this object is known to have an inconsistent setup for Hash and RecursiveRemove (i.e. More...

virtual void	Info (const char method, const char msgfmt,...) const
	Issue info message. More...

virtual Bool_t	InheritsFrom (const char *classname) const
	Returns kTRUE if object inherits from class "classname". More...

virtual Bool_t	InheritsFrom (const TClass *cl) const
	Returns kTRUE if object inherits from TClass cl. More...

virtual void	Inspect () const
	Dump contents of this object in a graphics canvas. More...

void	InvertBit (UInt_t f)

virtual Bool_t	IsEqual (const TObject *obj) const
	Default equal comparison (objects are equal if they have the same address in memory). More...

R__ALWAYS_INLINE Bool_t	IsOnHeap () const

R__ALWAYS_INLINE Bool_t	IsZombie () const

void	MayNotUse (const char *method) const
	Use this method to signal that a method (defined in a base class) may not be called in a derived class (in principle against good design since a child class should not provide less functionality than its parent, however, sometimes it is necessary). More...

virtual Bool_t	Notify ()
	This method must be overridden to handle object notification. More...

void	Obsolete (const char method, const char asOfVers, const char *removedFromVers) const
	Use this method to declare a method obsolete. More...

void	operator delete (void *ptr)
	Operator delete. More...

void	operator delete[] (void *ptr)
	Operator delete []. More...

void *	operator new (size_t sz)

void *	operator new (size_t sz, void *vp)

void *	operator new[] (size_t sz)

void *	operator new[] (size_t sz, void *vp)

TObject &	operator= (const TObject &rhs)
	TObject assignment operator. More...

virtual void	Paint (Option_t *option="")
	This method must be overridden if a class wants to paint itself. More...

virtual void	Pop ()
	Pop on object drawn in a pad to the top of the display list. More...

virtual Int_t	Read (const char *name)
	Read contents of object with specified name from the current directory. More...

virtual void	RecursiveRemove (TObject *obj)
	Recursively remove this object from a list. More...

void	ResetBit (UInt_t f)

virtual void	SaveAs (const char filename="", Option_t option="") const
	Save this object in the file specified by filename. More...

virtual void	SavePrimitive (std::ostream &out, Option_t *option="")
	Save a primitive as a C++ statement(s) on output stream "out". More...

void	SetBit (UInt_t f, Bool_t set)
	Set or unset the user status bits as specified in f. More...

void	SetBit (UInt_t f)

virtual void	SetDrawOption (Option_t *option="")
	Set drawing option for object. More...

virtual void	SetUniqueID (UInt_t uid)
	Set the unique object id. More...

virtual void	SysError (const char method, const char msgfmt,...) const
	Issue system error message. More...

R__ALWAYS_INLINE Bool_t	TestBit (UInt_t f) const

Int_t	TestBits (UInt_t f) const

virtual void	UseCurrentStyle ()
	Set current style settings in this object This function is called when either TCanvas::UseCurrentStyle or TROOT::ForceStyle have been invoked. More...

virtual void	Warning (const char method, const char msgfmt,...) const
	Issue warning message. More...

virtual Int_t	Write (const char *name=0, Int_t option=0, Int_t bufsize=0)
	Write this object to the current directory. More...

virtual Int_t	Write (const char *name=0, Int_t option=0, Int_t bufsize=0) const
	Write this object to the current directory. More...

Static Public Member Functions
static TMultiDimFit *	Instance ()
	Return the static instance. More...

Static Public Member Functions inherited from TObject
static Long_t	GetDtorOnly ()
	Return destructor only flag. More...

static Bool_t	GetObjectStat ()
	Get status of object stat flag. More...

static void	SetDtorOnly (void *obj)
	Set destructor only flag. More...

static void	SetObjectStat (Bool_t stat)
	Turn on/off tracking of objects in the TObjectTable. More...

Protected Member Functions
virtual Double_t	EvalControl (const Int_t *powers) const
	PRIVATE METHOD: Calculate the control parameter from the passed powers. More...

virtual Double_t	EvalFactor (Int_t p, Double_t x) const
	PRIVATE METHOD: Evaluate function with power p at variable value x. More...

virtual void	MakeCandidates ()
	PRIVATE METHOD: Create list of candidate functions for the parameterisation. More...

virtual void	MakeCoefficientErrors ()
	PRIVATE METHOD: Compute the errors on the coefficients. More...

virtual void	MakeCoefficients ()
	PRIVATE METHOD: Invert the model matrix B, and compute final coefficients. More...

virtual void	MakeCorrelation ()
	PRIVATE METHOD: Compute the correlation matrix. More...

virtual Double_t	MakeGramSchmidt (Int_t function)
	PRIVATE METHOD: Make Gram-Schmidt orthogonalisation. More...

virtual void	MakeNormalized ()
	PRIVATE METHOD: Normalize data to the interval [-1;1]. More...

virtual void	MakeParameterization ()
	PRIVATE METHOD: Find the parameterization over the training sample. More...

virtual void	MakeRealCode (const char filename, const char classname, Option_t *option="")
	PRIVATE METHOD: This is the method that actually generates the code for the evaluation the parameterization on some point. More...

virtual Bool_t	Select (const Int_t *iv)
	Selection method. More...

virtual Bool_t	TestFunction (Double_t squareResidual, Double_t dResidur)
	PRIVATE METHOD: Test whether the currently considered function contributes to the fit. More...

Protected Member Functions inherited from TObject
virtual void	DoError (int level, const char location, const char fmt, va_list va) const
	Interface to ErrorHandler (protected). More...

void	MakeZombie ()

Protected Attributes
Int_t	fBinVarX

Int_t	fBinVarY

Double_t	fChi2

TVectorD	fCoefficients

TVectorD	fCoefficientsRMS

Double_t	fCorrelationCoeff

TMatrixD	fCorrelationMatrix

Double_t	fError

TVirtualFitter *	fFitter

Int_t *	fFunctionCodes

TMatrixD	fFunctions

Byte_t	fHistogramMask

TList *	fHistograms

Bool_t	fIsUserFunction

Bool_t	fIsVerbose

Double_t	fMaxAngle

Int_t	fMaxFuncNV

Int_t	fMaxFunctions

Int_t *	fMaxPowers

Int_t *	fMaxPowersFinal

Double_t	fMaxQuantity

Double_t	fMaxResidual

Int_t	fMaxResidualRow

Int_t	fMaxStudy

Int_t	fMaxTerms

TVectorD	fMaxVariables

Double_t	fMeanQuantity

TVectorD	fMeanVariables

Double_t	fMinAngle

Double_t	fMinQuantity

Double_t	fMinRelativeError

Double_t	fMinResidual

Int_t	fMinResidualRow

TVectorD	fMinVariables

Int_t	fNCoefficients

Int_t	fNVariables

TVectorD	fOrthCoefficients

TMatrixD	fOrthCurvatureMatrix

TVectorD	fOrthFunctionNorms

TMatrixD	fOrthFunctions

Int_t	fParameterisationCode

EMDFPolyType	fPolyType
	Fit object (MINUIT) More...

Int_t *	fPowerIndex

Double_t	fPowerLimit

Int_t *	fPowers

Double_t	fPrecision

TVectorD	fQuantity

TVectorD	fResiduals

Double_t	fRMS

Int_t	fSampleSize

Bool_t	fShowCorrelation

TVectorD	fSqError

Double_t	fSumSqAvgQuantity

Double_t	fSumSqQuantity

Double_t	fSumSqResidual

Double_t	fTestCorrelationCoeff

Double_t	fTestError

Double_t	fTestPrecision

TVectorD	fTestQuantity

Int_t	fTestSampleSize

TVectorD	fTestSqError

TVectorD	fTestVariables

TVectorD	fVariables

Protected Attributes inherited from TNamed
TString	fName

TString	fTitle

Static Private Attributes
static TMultiDimFit *	fgInstance = 0

#include <TMultiDimFit.h>

Inheritance diagram for TMultiDimFit:

[legend]

Member Enumeration Documentation

◆ EMDFPolyType

enum TMultiDimFit::EMDFPolyType

Enumerator
kMonomials
kChebyshev
kLegendre

Definition at line 18 of file TMultiDimFit.h.

Constructor & Destructor Documentation

◆ TMultiDimFit() [1/2]

TMultiDimFit::TMultiDimFit ( )

Empty CTOR. Do not use.

Definition at line 430 of file TMultiDimFit.cxx.

◆ TMultiDimFit() [2/2]

TMultiDimFit::TMultiDimFit	(	Int_t	dimension,
		EMDFPolyType	type = `kMonomials`,
		Option_t *	option = `""`
	)

Constructor Second argument is the type of polynomials to use in parameterisation, one of: TMultiDimFit::kMonomials TMultiDimFit::kChebyshev TMultiDimFit::kLegendre.

Options: K Compute (k)correlation matrix V Be verbose

Default is no options.

Definition at line 505 of file TMultiDimFit.cxx.

◆ ~TMultiDimFit()

TMultiDimFit::~TMultiDimFit ( )

virtual

Destructor.

Definition at line 583 of file TMultiDimFit.cxx.

Member Function Documentation

◆ AddRow()

void TMultiDimFit::AddRow	(	const Double_t *	x,
		Double_t	D,
		Double_t	E = `0`
	)

virtual

Add a row consisting of fNVariables independent variables, the known, dependent quantity, and optionally, the square error in the dependent quantity, to the training sample to be used for the parameterization.

The mean of the variables and quantity is calculated on the fly, as outlined in TPrincipal::AddRow. This sample should be representative of the problem at hand. Please note, that if no error is given Poisson statistics is assumed and the square error is set to the value of dependent quantity. See also the class description

Definition at line 608 of file TMultiDimFit.cxx.

◆ AddTestRow()

void TMultiDimFit::AddTestRow	(	const Double_t *	x,
		Double_t	D,
		Double_t	E = `0`
	)

virtual

Add a row consisting of fNVariables independent variables, the known, dependent quantity, and optionally, the square error in the dependent quantity, to the test sample to be used for the test of the parameterization.

This sample needn't be representative of the problem at hand. Please note, that if no error is given Poisson statistics is assumed and the square error is set to the value of dependent quantity. See also the class description

Definition at line 687 of file TMultiDimFit.cxx.

◆ Browse()

void TMultiDimFit::Browse ( TBrowser * b )

virtual

Browse the TMultiDimFit object in the TBrowser.

Reimplemented from TObject.

Definition at line 734 of file TMultiDimFit.cxx.

◆ Clear()

void TMultiDimFit::Clear ( Option_t * option = "" )

virtual

Clear internal structures and variables.

Reimplemented from TNamed.

Definition at line 786 of file TMultiDimFit.cxx.

◆ Draw()

virtual void TMultiDimFit::Draw ( Option_t * option = "d" )

inlinevirtual

Default Draw method for all objects.

Reimplemented from TObject.

Definition at line 134 of file TMultiDimFit.h.

◆ Eval()

Double_t TMultiDimFit::Eval	(	const Double_t *	x,
		const Double_t *	coeff = `0`
	)		const

virtual

Evaluate parameterization at point x.

Optional argument coeff is a vector of coefficients for the parameterisation, fNCoefficients elements long.

Definition at line 873 of file TMultiDimFit.cxx.

◆ EvalControl()

Double_t TMultiDimFit::EvalControl ( const Int_t * powers ) const

protectedvirtual

PRIVATE METHOD: Calculate the control parameter from the passed powers.

Definition at line 934 of file TMultiDimFit.cxx.

◆ EvalError()

Double_t TMultiDimFit::EvalError	(	const Double_t *	x,
		const Double_t *	coeff = `0`
	)		const

virtual

Evaluate parameterization error at point x.

Optional argument coeff is a vector of coefficients for the parameterisation, fNCoefficients elements long.

Definition at line 901 of file TMultiDimFit.cxx.

◆ EvalFactor()

Double_t TMultiDimFit::EvalFactor	(	Int_t	p,
		Double_t	x
	)		const

protectedvirtual

PRIVATE METHOD: Evaluate function with power p at variable value x.

Definition at line 949 of file TMultiDimFit.cxx.

◆ FindParameterization()

void TMultiDimFit::FindParameterization ( Option_t * option = "" )

virtual

Find the parameterization.

Options: None so far

For detailed description of what this entails, please refer to the class description

Definition at line 991 of file TMultiDimFit.cxx.

◆ Fit()

void TMultiDimFit::Fit ( Option_t * option = "" )

virtual

Try to fit the found parameterisation to the test sample.

Options M use Minuit to improve coefficients

Also, refer to class description

Definition at line 1010 of file TMultiDimFit.cxx.

◆ GetChi2()

Double_t TMultiDimFit::GetChi2 ( ) const

inline

Definition at line 140 of file TMultiDimFit.h.

◆ GetCoefficients()

const TVectorD* TMultiDimFit::GetCoefficients ( ) const

inline

Definition at line 142 of file TMultiDimFit.h.

◆ GetCoefficientsRMS()

const TVectorD* TMultiDimFit::GetCoefficientsRMS ( ) const

inline

Definition at line 143 of file TMultiDimFit.h.

◆ GetCorrelationMatrix()

const TMatrixD* TMultiDimFit::GetCorrelationMatrix ( ) const

inline

Definition at line 141 of file TMultiDimFit.h.

◆ GetError()

Double_t TMultiDimFit::GetError ( ) const

inline

Definition at line 144 of file TMultiDimFit.h.

◆ GetFunctionCodes()

Int_t* TMultiDimFit::GetFunctionCodes ( ) const

inline

Definition at line 145 of file TMultiDimFit.h.

◆ GetFunctions()

const TMatrixD* TMultiDimFit::GetFunctions ( ) const

inline

Definition at line 146 of file TMultiDimFit.h.

◆ GetHistograms()

virtual TList* TMultiDimFit::GetHistograms ( ) const

inlinevirtual

Definition at line 147 of file TMultiDimFit.h.

◆ GetMaxAngle()

Double_t TMultiDimFit::GetMaxAngle ( ) const

inline

Definition at line 148 of file TMultiDimFit.h.

◆ GetMaxFunctions()

Int_t TMultiDimFit::GetMaxFunctions ( ) const

inline

Definition at line 149 of file TMultiDimFit.h.

◆ GetMaxPowers()

Int_t* TMultiDimFit::GetMaxPowers ( ) const

inline

Definition at line 150 of file TMultiDimFit.h.

◆ GetMaxQuantity()

Double_t TMultiDimFit::GetMaxQuantity ( ) const

inline

Definition at line 151 of file TMultiDimFit.h.

◆ GetMaxStudy()

Int_t TMultiDimFit::GetMaxStudy ( ) const

inline

Definition at line 152 of file TMultiDimFit.h.

◆ GetMaxTerms()

Int_t TMultiDimFit::GetMaxTerms ( ) const

inline

Definition at line 153 of file TMultiDimFit.h.

◆ GetMaxVariables()

const TVectorD* TMultiDimFit::GetMaxVariables ( ) const

inline

Definition at line 154 of file TMultiDimFit.h.

◆ GetMeanQuantity()

Double_t TMultiDimFit::GetMeanQuantity ( ) const

inline

Definition at line 155 of file TMultiDimFit.h.

◆ GetMeanVariables()

const TVectorD* TMultiDimFit::GetMeanVariables ( ) const

inline

Definition at line 156 of file TMultiDimFit.h.

◆ GetMinAngle()

Double_t TMultiDimFit::GetMinAngle ( ) const

inline

Definition at line 157 of file TMultiDimFit.h.

◆ GetMinQuantity()

Double_t TMultiDimFit::GetMinQuantity ( ) const

inline

Definition at line 158 of file TMultiDimFit.h.

◆ GetMinRelativeError()

Double_t TMultiDimFit::GetMinRelativeError ( ) const

inline

Definition at line 159 of file TMultiDimFit.h.

◆ GetMinVariables()

const TVectorD* TMultiDimFit::GetMinVariables ( ) const

inline

Definition at line 160 of file TMultiDimFit.h.

◆ GetNCoefficients()

Int_t TMultiDimFit::GetNCoefficients ( ) const

inline

Definition at line 162 of file TMultiDimFit.h.

◆ GetNVariables()

Int_t TMultiDimFit::GetNVariables ( ) const

inline

Definition at line 161 of file TMultiDimFit.h.

◆ GetPolyType()

Int_t TMultiDimFit::GetPolyType ( ) const

inline

Definition at line 163 of file TMultiDimFit.h.

◆ GetPowerIndex()

Int_t* TMultiDimFit::GetPowerIndex ( ) const

inline

Definition at line 164 of file TMultiDimFit.h.

◆ GetPowerLimit()

Double_t TMultiDimFit::GetPowerLimit ( ) const

inline

Definition at line 165 of file TMultiDimFit.h.

◆ GetPowers()

const Int_t* TMultiDimFit::GetPowers ( ) const

inline

Definition at line 166 of file TMultiDimFit.h.

◆ GetPrecision()

Double_t TMultiDimFit::GetPrecision ( ) const

inline

Definition at line 167 of file TMultiDimFit.h.

◆ GetQuantity()

const TVectorD* TMultiDimFit::GetQuantity ( ) const

inline

Definition at line 168 of file TMultiDimFit.h.

◆ GetResidualMax()

Double_t TMultiDimFit::GetResidualMax ( ) const

inline

Definition at line 169 of file TMultiDimFit.h.

◆ GetResidualMaxRow()

Int_t TMultiDimFit::GetResidualMaxRow ( ) const

inline

Definition at line 171 of file TMultiDimFit.h.

◆ GetResidualMin()

Double_t TMultiDimFit::GetResidualMin ( ) const

inline

Definition at line 170 of file TMultiDimFit.h.

◆ GetResidualMinRow()

Int_t TMultiDimFit::GetResidualMinRow ( ) const

inline

Definition at line 172 of file TMultiDimFit.h.

◆ GetResidualSumSq()

Double_t TMultiDimFit::GetResidualSumSq ( ) const

inline

Definition at line 173 of file TMultiDimFit.h.

◆ GetRMS()

Double_t TMultiDimFit::GetRMS ( ) const

inline

Definition at line 174 of file TMultiDimFit.h.

◆ GetSampleSize()

Int_t TMultiDimFit::GetSampleSize ( ) const

inline

Definition at line 175 of file TMultiDimFit.h.

◆ GetSqError()

const TVectorD* TMultiDimFit::GetSqError ( ) const

inline

Definition at line 176 of file TMultiDimFit.h.

◆ GetSumSqAvgQuantity()

Double_t TMultiDimFit::GetSumSqAvgQuantity ( ) const

inline

Definition at line 177 of file TMultiDimFit.h.

◆ GetSumSqQuantity()

Double_t TMultiDimFit::GetSumSqQuantity ( ) const

inline

Definition at line 178 of file TMultiDimFit.h.

◆ GetTestError()

Double_t TMultiDimFit::GetTestError ( ) const

inline

Definition at line 179 of file TMultiDimFit.h.

◆ GetTestPrecision()

Double_t TMultiDimFit::GetTestPrecision ( ) const

inline

Definition at line 180 of file TMultiDimFit.h.

◆ GetTestQuantity()

const TVectorD* TMultiDimFit::GetTestQuantity ( ) const

inline

Definition at line 181 of file TMultiDimFit.h.

◆ GetTestSampleSize()

Int_t TMultiDimFit::GetTestSampleSize ( ) const

inline

Definition at line 182 of file TMultiDimFit.h.

◆ GetTestSqError()

const TVectorD* TMultiDimFit::GetTestSqError ( ) const

inline

Definition at line 183 of file TMultiDimFit.h.

◆ GetTestVariables()

const TVectorD* TMultiDimFit::GetTestVariables ( ) const

inline

Definition at line 184 of file TMultiDimFit.h.

◆ GetVariables()

const TVectorD* TMultiDimFit::GetVariables ( ) const

inline

Definition at line 185 of file TMultiDimFit.h.

◆ Instance()

TMultiDimFit * TMultiDimFit::Instance ( )

static

Return the static instance.

Definition at line 1091 of file TMultiDimFit.cxx.

◆ IsFolder()

virtual Bool_t TMultiDimFit::IsFolder ( ) const

inlinevirtual

Returns kTRUE in case object contains browsable objects (like containers or lists of other objects).

Reimplemented from TObject.

Definition at line 188 of file TMultiDimFit.h.

◆ MakeCandidates()

void TMultiDimFit::MakeCandidates ( )

protectedvirtual

PRIVATE METHOD: Create list of candidate functions for the parameterisation.

See also class description

Definition at line 1102 of file TMultiDimFit.cxx.

◆ MakeChi2()

Double_t TMultiDimFit::MakeChi2 ( const Double_t * coeff = 0 )

virtual

Calculate Chi square over either the test sample.

The optional argument coeff is a vector of coefficients to use in the evaluation of the parameterisation. If coeff == 0, then the found coefficients is used. Used my MINUIT for fit (see TMultDimFit::Fit)

Definition at line 1237 of file TMultiDimFit.cxx.

◆ MakeCode()

void TMultiDimFit::MakeCode	(	const char *	filename = `"MDF"`,
		Option_t *	option = `""`
	)

virtual

Generate the file <filename> with .C appended if argument doesn't end in .cxx or .C.

The contains the implementation of the function:

Double_t <funcname>(Double_t *x)

which does the same as TMultiDimFit::Eval. Please refer to this method.

Further, the static variables:

Int_t    gNVariables
Int_t    gNCoefficients
Double_t gDMean
Double_t gXMean[]
Double_t gXMin[]
Double_t gXMax[]
Double_t gCoefficient[]
Int_t    gPower[]

are initialized. The only ROOT header file needed is Rtypes.h

See TMultiDimFit::MakeRealCode for a list of options

Definition at line 1287 of file TMultiDimFit.cxx.

◆ MakeCoefficientErrors()

void TMultiDimFit::MakeCoefficientErrors ( )

protectedvirtual

PRIVATE METHOD: Compute the errors on the coefficients.

For this to be done, the curvature matrix of the non-orthogonal functions, is computed.

Definition at line 1304 of file TMultiDimFit.cxx.

◆ MakeCoefficients()

void TMultiDimFit::MakeCoefficients ( )

protectedvirtual

PRIVATE METHOD: Invert the model matrix B, and compute final coefficients.

For a more thorough discussion of what this means, please refer to the class description

First we invert the lower triangle matrix fOrthCurvatureMatrix and store the inverted matrix in the upper triangle.

Definition at line 1362 of file TMultiDimFit.cxx.

◆ MakeCorrelation()

void TMultiDimFit::MakeCorrelation ( )

protectedvirtual

PRIVATE METHOD: Compute the correlation matrix.

Definition at line 1442 of file TMultiDimFit.cxx.

◆ MakeGramSchmidt()

Double_t TMultiDimFit::MakeGramSchmidt ( Int_t function )

protectedvirtual

PRIVATE METHOD: Make Gram-Schmidt orthogonalisation.

The class description gives a thorough account of this algorithm, as well as references. Please refer to the class description

Definition at line 1501 of file TMultiDimFit.cxx.

◆ MakeHistograms()

void TMultiDimFit::MakeHistograms ( Option_t * option = "A" )

virtual

Make histograms of the result of the analysis.

This message should be sent after having read all data points, but before finding the parameterization

Options: A All the below X Original independent variables D Original dependent variables N Normalised independent variables S Shifted dependent variables R1 Residuals versus normalised independent variables R2 Residuals versus dependent variable R3 Residuals computed on training sample R4 Residuals computed on test sample

For a description of these quantities, refer to class description

Definition at line 1594 of file TMultiDimFit.cxx.

◆ MakeMethod()

void TMultiDimFit::MakeMethod	(	const Char_t *	classname = `"MDF"`,
		Option_t *	option = `""`
	)

virtual

Generate the file <classname>MDF.cxx which contains the implementation of the method:

Double_t <classname>MDF(Double_t *x)

which does the same as TMultiDimFit::Eval. Please refer to this method.

Further, the public static members:

Int_t <classname>::fgNVariables Int_t <classname>::fgNCoefficients Double_t <classname>::fgDMean Double_t <classname>::fgXMean[] //[fgNVariables] Double_t <classname>::fgXMin[] //[fgNVariables] Double_t <classname>::fgXMax[] //[fgNVariables] Double_t <classname>::fgCoefficient[] //[fgNCoeffficents] Int_t <classname>::fgPower[] //[fgNCoeffficents*fgNVariables]

are initialized, and assumed to exist. The class declaration is assumed to be in <classname>.h and assumed to be provided by the user.

See TMultiDimFit::MakeRealCode for a list of options

The minimal class definition is:

class <classname> { public: Int_t <classname>::fgNVariables; // Number of variables Int_t <classname>::fgNCoefficients; // Number of terms Double_t <classname>::fgDMean; // Mean from training sample Double_t <classname>::fgXMean[]; // Mean from training sample Double_t <classname>::fgXMin[]; // Min from training sample Double_t <classname>::fgXMax[]; // Max from training sample Double_t <classname>::fgCoefficient[]; // Coefficients Int_t <classname>::fgPower[]; // Function powers

Double_t Eval(Double_t *x); };

Whether the method <classname>::Eval should be static or not, is up to the user.

Definition at line 1739 of file TMultiDimFit.cxx.

◆ MakeNormalized()

void TMultiDimFit::MakeNormalized ( )

protectedvirtual

PRIVATE METHOD: Normalize data to the interval [-1;1].

This is needed for the classes method to work.

Definition at line 1751 of file TMultiDimFit.cxx.

◆ MakeParameterization()

void TMultiDimFit::MakeParameterization ( )

protectedvirtual

PRIVATE METHOD: Find the parameterization over the training sample.

A full account of the algorithm is given in the class description

Definition at line 1805 of file TMultiDimFit.cxx.

◆ MakeRealCode()

void TMultiDimFit::MakeRealCode	(	const char *	filename,
		const char *	classname,
		Option_t *	option = `""`
	)

protectedvirtual

PRIVATE METHOD: This is the method that actually generates the code for the evaluation the parameterization on some point.

It's called by TMultiDimFit::MakeCode and TMultiDimFit::MakeMethod.

The options are: NONE so far

Definition at line 1958 of file TMultiDimFit.cxx.

◆ Print()

void TMultiDimFit::Print ( Option_t * option = "ps" ) const

virtual

Print statistics etc.

Options are P Parameters S Statistics C Coefficients R Result of parameterisation F Result of fit K Correlation Matrix M Pretty print formula

Reimplemented from TNamed.

Definition at line 2151 of file TMultiDimFit.cxx.

◆ Select()

Bool_t TMultiDimFit::Select ( const Int_t * iv )

protectedvirtual

Selection method.

User can override this method for specialized selection of acceptable functions in fit. Default is to select all. This message is sent during the build-up of the function candidates table once for each set of powers in variables. Notice, that the argument array contains the powers PLUS ONE. For example, to De select the function f = x1^2 * x2^4 * x3^5, this method should return kFALSE if given the argument { 3, 4, 6 }

Definition at line 2358 of file TMultiDimFit.cxx.

◆ SetBinVarX()

void TMultiDimFit::SetBinVarX ( Int_t nbbinvarx )

inline

Definition at line 195 of file TMultiDimFit.h.

◆ SetBinVarY()

void TMultiDimFit::SetBinVarY ( Int_t nbbinvary )

inline

Definition at line 196 of file TMultiDimFit.h.

◆ SetMaxAngle()

void TMultiDimFit::SetMaxAngle ( Double_t ang = 0 )

Set the max angle (in degrees) between the initial data vector to be fitted, and the new candidate function to be included in the fit.

By default it is 0, which automatically chooses another selection criteria. See also class description

Definition at line 2370 of file TMultiDimFit.cxx.

◆ SetMaxFunctions()

void TMultiDimFit::SetMaxFunctions ( Int_t n )

inline

Definition at line 198 of file TMultiDimFit.h.

◆ SetMaxPowers()

void TMultiDimFit::SetMaxPowers ( const Int_t * powers )

Set the maximum power to be considered in the fit for each variable.

See also class description

Definition at line 2436 of file TMultiDimFit.cxx.

◆ SetMaxStudy()

void TMultiDimFit::SetMaxStudy ( Int_t n )

inline

Definition at line 200 of file TMultiDimFit.h.

◆ SetMaxTerms()

void TMultiDimFit::SetMaxTerms ( Int_t terms )

inline

Definition at line 201 of file TMultiDimFit.h.

◆ SetMinAngle()

void TMultiDimFit::SetMinAngle ( Double_t ang = 1 )

Set the min angle (in degrees) between a new candidate function and the subspace spanned by the previously accepted functions.

See also class description

Definition at line 2386 of file TMultiDimFit.cxx.

◆ SetMinRelativeError()

void TMultiDimFit::SetMinRelativeError ( Double_t error )

Set the acceptable relative error for when sum of square residuals is considered minimized.

For a full account, refer to the class description

Definition at line 2451 of file TMultiDimFit.cxx.

◆ SetPowerLimit()

void TMultiDimFit::SetPowerLimit ( Double_t limit = 1e-3 )

Set the user parameter for the function selection.

The bigger the limit, the more functions are used. The meaning of this variable is defined in the class description

Definition at line 2426 of file TMultiDimFit.cxx.

◆ SetPowers()

void TMultiDimFit::SetPowers	(	const Int_t *	powers,
		Int_t	terms
	)

virtual

Define a user function.

The input array must be of the form (p11, ..., p1N, ... ,pL1, ..., pLN) Where N is the dimension of the data sample, L is the number of terms (given in terms) and the first number, labels the term, the second the variable. More information is given in the class description

Definition at line 2406 of file TMultiDimFit.cxx.

◆ TestFunction()

Bool_t TMultiDimFit::TestFunction	(	Double_t	squareResidual,
		Double_t	dResidur
	)

protectedvirtual

PRIVATE METHOD: Test whether the currently considered function contributes to the fit.

See also class description

Definition at line 2463 of file TMultiDimFit.cxx.

Member Data Documentation

◆ fBinVarX

Int_t TMultiDimFit::fBinVarX

protected

Definition at line 98 of file TMultiDimFit.h.

◆ fBinVarY

Int_t TMultiDimFit::fBinVarY

protected

Definition at line 99 of file TMultiDimFit.h.

◆ fChi2

Double_t TMultiDimFit::fChi2

protected

Definition at line 85 of file TMultiDimFit.h.

◆ fCoefficients

TVectorD TMultiDimFit::fCoefficients

protected

Definition at line 82 of file TMultiDimFit.h.

◆ fCoefficientsRMS

TVectorD TMultiDimFit::fCoefficientsRMS

protected

Definition at line 83 of file TMultiDimFit.h.

◆ fCorrelationCoeff

Double_t TMultiDimFit::fCorrelationCoeff

protected

Definition at line 92 of file TMultiDimFit.h.

◆ fCorrelationMatrix

TMatrixD TMultiDimFit::fCorrelationMatrix

protected

Definition at line 93 of file TMultiDimFit.h.

◆ fError

Double_t TMultiDimFit::fError

protected

Definition at line 88 of file TMultiDimFit.h.

◆ fFitter

TVirtualFitter* TMultiDimFit::fFitter

protected

Definition at line 101 of file TMultiDimFit.h.

◆ fFunctionCodes

Int_t* TMultiDimFit::fFunctionCodes

protected

Definition at line 60 of file TMultiDimFit.h.

◆ fFunctions

TMatrixD TMultiDimFit::fFunctions

protected

Definition at line 58 of file TMultiDimFit.h.

◆ fgInstance

TMultiDimFit * TMultiDimFit::fgInstance = 0

staticprivate

Definition at line 25 of file TMultiDimFit.h.

◆ fHistogramMask

Byte_t TMultiDimFit::fHistogramMask

protected

Definition at line 97 of file TMultiDimFit.h.

◆ fHistograms

TList* TMultiDimFit::fHistograms

protected

Definition at line 96 of file TMultiDimFit.h.

◆ fIsUserFunction

Bool_t TMultiDimFit::fIsUserFunction

protected

Definition at line 105 of file TMultiDimFit.h.

◆ fIsVerbose

Bool_t TMultiDimFit::fIsVerbose

protected

Definition at line 106 of file TMultiDimFit.h.

◆ fMaxAngle

Double_t TMultiDimFit::fMaxAngle

protected

Definition at line 51 of file TMultiDimFit.h.

◆ fMaxFuncNV

Int_t TMultiDimFit::fMaxFuncNV

protected

Definition at line 62 of file TMultiDimFit.h.

◆ fMaxFunctions

Int_t TMultiDimFit::fMaxFunctions

protected

Definition at line 59 of file TMultiDimFit.h.

◆ fMaxPowers

Int_t* TMultiDimFit::fMaxPowers

protected

Definition at line 54 of file TMultiDimFit.h.

◆ fMaxPowersFinal

Int_t* TMultiDimFit::fMaxPowersFinal

protected

Definition at line 68 of file TMultiDimFit.h.

◆ fMaxQuantity

Double_t TMultiDimFit::fMaxQuantity

protected

Definition at line 31 of file TMultiDimFit.h.

◆ fMaxResidual

Double_t TMultiDimFit::fMaxResidual

protected

Definition at line 73 of file TMultiDimFit.h.

◆ fMaxResidualRow

Int_t TMultiDimFit::fMaxResidualRow

protected

Definition at line 75 of file TMultiDimFit.h.

◆ fMaxStudy

Int_t TMultiDimFit::fMaxStudy

protected

Definition at line 61 of file TMultiDimFit.h.

◆ fMaxTerms

Int_t TMultiDimFit::fMaxTerms

protected

Definition at line 52 of file TMultiDimFit.h.

◆ fMaxVariables

TVectorD TMultiDimFit::fMaxVariables

protected

Definition at line 39 of file TMultiDimFit.h.

◆ fMeanQuantity

Double_t TMultiDimFit::fMeanQuantity

protected

Definition at line 30 of file TMultiDimFit.h.

◆ fMeanVariables

TVectorD TMultiDimFit::fMeanVariables

protected

Definition at line 38 of file TMultiDimFit.h.

◆ fMinAngle

Double_t TMultiDimFit::fMinAngle

protected

Definition at line 50 of file TMultiDimFit.h.

◆ fMinQuantity

Double_t TMultiDimFit::fMinQuantity

protected

Definition at line 32 of file TMultiDimFit.h.

◆ fMinRelativeError

Double_t TMultiDimFit::fMinRelativeError

protected

Definition at line 53 of file TMultiDimFit.h.

◆ fMinResidual

Double_t TMultiDimFit::fMinResidual

protected

Definition at line 74 of file TMultiDimFit.h.

◆ fMinResidualRow

Int_t TMultiDimFit::fMinResidualRow

protected

Definition at line 76 of file TMultiDimFit.h.

◆ fMinVariables

TVectorD TMultiDimFit::fMinVariables

protected

Definition at line 40 of file TMultiDimFit.h.

◆ fNCoefficients

Int_t TMultiDimFit::fNCoefficients

protected

Definition at line 79 of file TMultiDimFit.h.

◆ fNVariables

Int_t TMultiDimFit::fNVariables

protected

Definition at line 37 of file TMultiDimFit.h.

◆ fOrthCoefficients

TVectorD TMultiDimFit::fOrthCoefficients

protected

Definition at line 80 of file TMultiDimFit.h.

◆ fOrthCurvatureMatrix

TMatrixD TMultiDimFit::fOrthCurvatureMatrix

protected

Definition at line 81 of file TMultiDimFit.h.

◆ fOrthFunctionNorms

TVectorD TMultiDimFit::fOrthFunctionNorms

protected

Definition at line 65 of file TMultiDimFit.h.

◆ fOrthFunctions

TMatrixD TMultiDimFit::fOrthFunctions

protected

Definition at line 64 of file TMultiDimFit.h.

◆ fParameterisationCode

Int_t TMultiDimFit::fParameterisationCode

protected

Definition at line 86 of file TMultiDimFit.h.

◆ fPolyType

EMDFPolyType TMultiDimFit::fPolyType

protected

Fit object (MINUIT)

Definition at line 103 of file TMultiDimFit.h.

◆ fPowerIndex

Int_t* TMultiDimFit::fPowerIndex

protected

Definition at line 70 of file TMultiDimFit.h.

◆ fPowerLimit

Double_t TMultiDimFit::fPowerLimit

protected

Definition at line 55 of file TMultiDimFit.h.

◆ fPowers

Int_t* TMultiDimFit::fPowers

protected

Definition at line 69 of file TMultiDimFit.h.

◆ fPrecision

Double_t TMultiDimFit::fPrecision

protected

Definition at line 90 of file TMultiDimFit.h.

◆ fQuantity

TVectorD TMultiDimFit::fQuantity

protected

Definition at line 28 of file TMultiDimFit.h.

◆ fResiduals

TVectorD TMultiDimFit::fResiduals

protected

Definition at line 72 of file TMultiDimFit.h.

◆ fRMS

Double_t TMultiDimFit::fRMS

protected

Definition at line 84 of file TMultiDimFit.h.

◆ fSampleSize

Int_t TMultiDimFit::fSampleSize

protected

Definition at line 42 of file TMultiDimFit.h.

◆ fShowCorrelation

Bool_t TMultiDimFit::fShowCorrelation

protected

Definition at line 104 of file TMultiDimFit.h.

◆ fSqError

TVectorD TMultiDimFit::fSqError

protected

Definition at line 29 of file TMultiDimFit.h.

◆ fSumSqAvgQuantity

Double_t TMultiDimFit::fSumSqAvgQuantity

protected

Definition at line 34 of file TMultiDimFit.h.

◆ fSumSqQuantity

Double_t TMultiDimFit::fSumSqQuantity

protected

Definition at line 33 of file TMultiDimFit.h.

◆ fSumSqResidual

Double_t TMultiDimFit::fSumSqResidual

protected

Definition at line 77 of file TMultiDimFit.h.

◆ fTestCorrelationCoeff

Double_t TMultiDimFit::fTestCorrelationCoeff

protected

Definition at line 94 of file TMultiDimFit.h.

◆ fTestError

Double_t TMultiDimFit::fTestError

protected

Definition at line 89 of file TMultiDimFit.h.

◆ fTestPrecision

Double_t TMultiDimFit::fTestPrecision

protected

Definition at line 91 of file TMultiDimFit.h.

◆ fTestQuantity

TVectorD TMultiDimFit::fTestQuantity

protected

Definition at line 44 of file TMultiDimFit.h.

◆ fTestSampleSize

Int_t TMultiDimFit::fTestSampleSize

protected

Definition at line 48 of file TMultiDimFit.h.

◆ fTestSqError

TVectorD TMultiDimFit::fTestSqError

protected

Definition at line 45 of file TMultiDimFit.h.

◆ fTestVariables

TVectorD TMultiDimFit::fTestVariables

protected

Definition at line 46 of file TMultiDimFit.h.

◆ fVariables

TVectorD TMultiDimFit::fVariables

protected

Definition at line 36 of file TMultiDimFit.h.

Libraries for TMultiDimFit:

[legend]

Overview

The Method

Limiting the Number of Terms

Gram-Schmidt Orthogonalisation

Function Selection Based on Residual

Test 1

Test 2

Coefficients and Coefficient Errors

Considerations

Testing the parameterization

Bibliography

Public Types

Public Member Functions

Static Public Member Functions

Protected Member Functions

Protected Attributes

Static Private Attributes

Member Enumeration Documentation

◆ EMDFPolyType

Constructor & Destructor Documentation

◆ TMultiDimFit() [1/2]

◆ TMultiDimFit() [2/2]

◆ ~TMultiDimFit()

Member Function Documentation

◆ AddRow()

◆ AddTestRow()

◆ Browse()

◆ Clear()

◆ Draw()

◆ Eval()

◆ EvalControl()

◆ EvalError()

◆ EvalFactor()

◆ FindParameterization()

◆ Fit()

◆ GetChi2()

◆ GetCoefficients()

◆ GetCoefficientsRMS()

◆ GetCorrelationMatrix()

◆ GetError()

◆ GetFunctionCodes()

◆ GetFunctions()

◆ GetHistograms()

◆ GetMaxAngle()

◆ GetMaxFunctions()

◆ GetMaxPowers()

◆ GetMaxQuantity()

◆ GetMaxStudy()

◆ GetMaxTerms()

◆ GetMaxVariables()

◆ GetMeanQuantity()

◆ GetMeanVariables()

◆ GetMinAngle()

◆ GetMinQuantity()

◆ GetMinRelativeError()

◆ GetMinVariables()

◆ GetNCoefficients()

◆ GetNVariables()

◆ GetPolyType()

◆ GetPowerIndex()

◆ GetPowerLimit()

◆ GetPowers()

◆ GetPrecision()

◆ GetQuantity()

◆ GetResidualMax()

◆ GetResidualMaxRow()

◆ GetResidualMin()

◆ GetResidualMinRow()

◆ GetResidualSumSq()

◆ GetRMS()

◆ GetSampleSize()

◆ GetSqError()

◆ GetSumSqAvgQuantity()

◆ GetSumSqQuantity()

◆ GetTestError()

◆ GetTestPrecision()

◆ GetTestQuantity()

◆ GetTestSampleSize()

◆ GetTestSqError()

◆ GetTestVariables()