doc/master/rf403__weightedevts_8py.html

from __future__ import print_function

import ROOT


# Create observable and unweighted dataset

# -------------------------------------------


# Declare observable

x = ROOT.RooRealVar("x", "x", -10, 10)

x.setBins(40)


# Construction a uniform pdf

p0 = ROOT.RooPolynomial("px", "px", x)


# Sample 1000 events from pdf

data = p0.generate({x}, 1000)


# Calculate weight and make dataset weighted

# --------------------------------------------------


# Construct formula to calculate (fake) weight for events

wFunc = ROOT.RooFormulaVar("w", "event weight", "(x*x+10)", [x])


# Add column with variable w to previously generated dataset

w = data.addColumn(wFunc)


# Dataset d is now a dataset with two observable (x,w) with 1000 entries

data.Print()


# Instruct dataset wdata in interpret w as event weight rather than as

# observable

wdata = ROOT.RooDataSet(data.GetName(), data.GetTitle(), data, data.get(), "", w.GetName())


# Dataset d is now a dataset with one observable (x) with 1000 entries and

# a sum of weights of ~430K

wdata.Print()


# Unbinned ML fit to weighted data

# ---------------------------------------------------------------


# Construction quadratic polynomial pdf for fitting

a0 = ROOT.RooRealVar("a0", "a0", 1)

a1 = ROOT.RooRealVar("a1", "a1", 0, -1, 1)

a2 = ROOT.RooRealVar("a2", "a2", 1, 0, 10)

p2 = ROOT.RooPolynomial("p2", "p2", x, [a0, a1, a2], 0)


# Fit quadratic polynomial to weighted data


# NOTE: A plain Maximum likelihood fit to weighted data does in general

#       NOT result in correct error estimates, individual

#       event weights represent Poisson statistics themselves.

#

# Fit with 'wrong' errors

r_ml_wgt = p2.fitTo(wdata, Save=True)


# A first order correction to estimated parameter errors in an

# (unbinned) ML fit can be obtained by calculating the

# covariance matrix as

#

#    V' = V C-1 V

#

# where V is the covariance matrix calculated from a fit

# to -logL = - sum [ w_i log f(x_i) ] and C is the covariance

# matrix calculated from -logL' = -sum [ w_i^2 log f(x_i) ]

# (i.e. the weights are applied squared)

#

# A fit in self mode can be performed as follows:


r_ml_wgt_corr = p2.fitTo(wdata, Save=True, SumW2Error=True)


# Plot weighted data and fit result

# ---------------------------------------------------------------


# Construct plot frame

frame = x.frame(Title="Unbinned ML fit, chi^2 fit to weighted data")


# Plot data using sum-of-weights-squared error rather than Poisson errors

wdata.plotOn(frame, DataError="SumW2")


# Overlay result of 2nd order polynomial fit to weighted data

p2.plotOn(frame)


# ML fit of pdf to equivalent unweighted dataset

# ---------------------------------------------------------------------


# Construct a pdf with the same shape as p0 after weighting

genPdf = ROOT.RooGenericPdf("genPdf", "x*x+10", [x])


# Sample a dataset with the same number of events as data

data2 = genPdf.generate({x}, 1000)


# Sample a dataset with the same number of weights as data

data3 = genPdf.generate({x}, 43000)


# Fit the 2nd order polynomial to both unweighted datasets and save the

# results for comparison

r_ml_unw10 = p2.fitTo(data2, Save=True)

r_ml_unw43 = p2.fitTo(data3, Save=True)


# Chis2 fit of pdf to binned weighted dataset

# ---------------------------------------------------------------------------


# Construct binned clone of unbinned weighted dataset

binnedData = wdata.binnedClone()

binnedData.Print("v")


# Perform chi2 fit to binned weighted dataset using sum-of-weights errors

#

# NB: Within the usual approximations of a chi2 fit, chi2 fit to weighted

# data using sum-of-weights-squared errors does give correct error

# estimates

chi2 = p2.createChi2(binnedData, ROOT.RooFit.DataError("SumW2"))

m = ROOT.RooMinimizer(chi2)

m.migrad()

m.hesse()


# Plot chi^2 fit result on frame as well

r_chi2_wgt = m.save()

p2.plotOn(frame, LineStyle="--", LineColor="r")


# Compare fit results of chi2, L fits to (un)weighted data

# ------------------------------------------------------------


# Note that ML fit on 1Kevt of weighted data is closer to result of ML fit on 43Kevt of unweighted data

# than to 1Kevt of unweighted data, the reference chi^2 fit with SumW2 error gives a result closer to

# that of an unbinned ML fit to 1Kevt of unweighted data.


print("==> ML Fit results on 1K unweighted events")

r_ml_unw10.Print()

print("==> ML Fit results on 43K unweighted events")

r_ml_unw43.Print()

print("==> ML Fit results on 1K weighted events with a summed weight of 43K")

r_ml_wgt.Print()

print("==> Corrected ML Fit results on 1K weighted events with a summed weight of 43K")

r_ml_wgt_corr.Print()

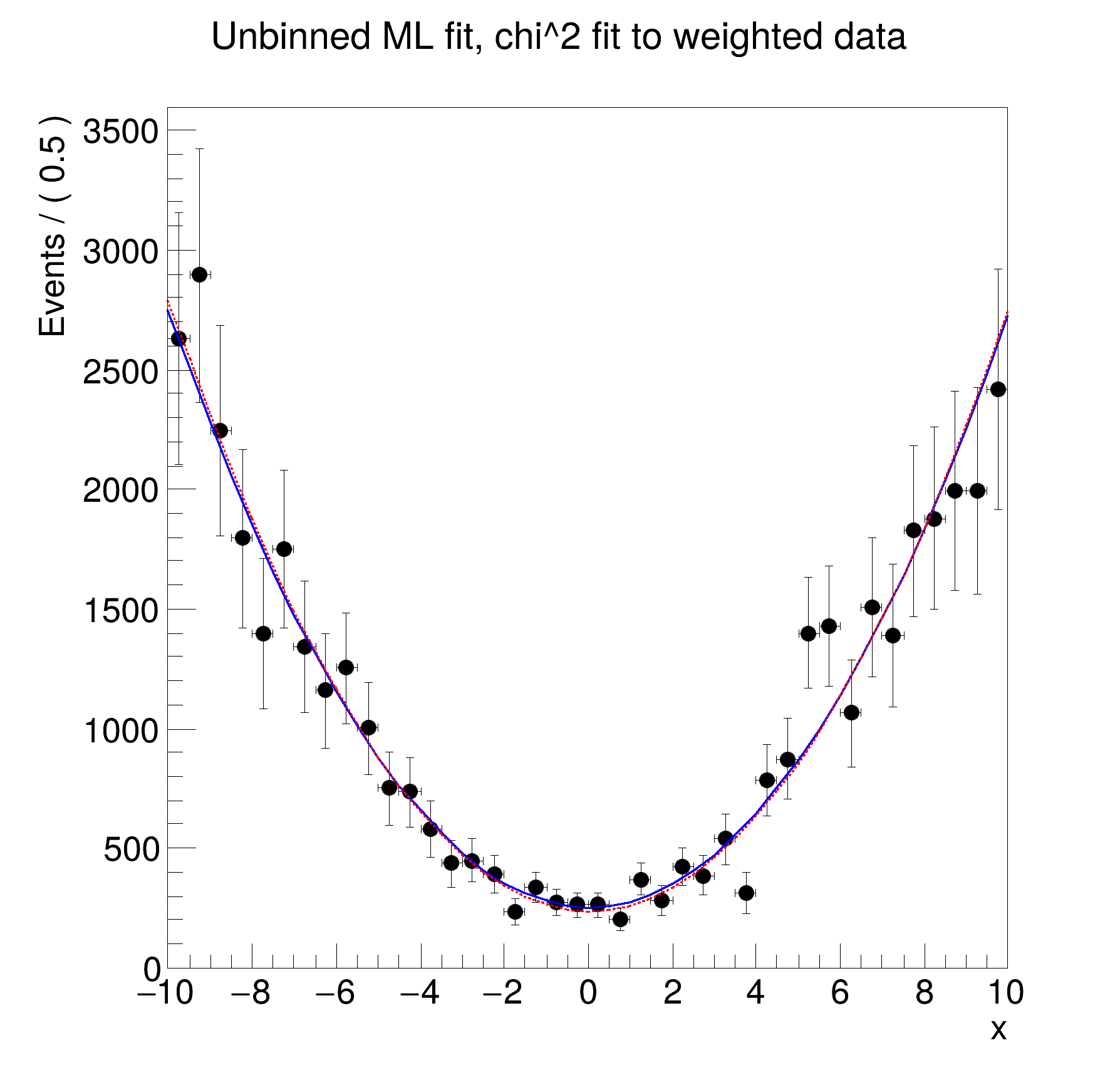
print("==> Chi2 Fit results on 1K weighted events with a summed weight of 43K")

r_chi2_wgt.Print()


c = ROOT.TCanvas("rf403_weightedevts", "rf403_weightedevts", 600, 600)

ROOT.gPad.SetLeftMargin(0.15)

frame.GetYaxis().SetTitleOffset(1.8)

frame.Draw()


c.SaveAs("rf403_weightedevts.png")